非合作通信中MQAM的定时载波联合同步

刘明骞， 陈 钱， 吴 芸， 李兵兵

(1. 西安电子科技大学 信息感知技术协同创新中心，陕西 西安 710071； 2. 南京理工大学 电子工程与光电技术学院，江苏 南京 210094; 3. 徐州雷奥医疗设备有限公司，江苏 徐州 221116)

非合作通信中MQAM的定时载波联合同步

刘明骞1,2,3， 陈 钱2， 吴 芸3， 李兵兵1

(1. 西安电子科技大学 信息感知技术协同创新中心，陕西 西安 710071； 2. 南京理工大学 电子工程与光电技术学院，江苏 南京 210094; 3. 徐州雷奥医疗设备有限公司，江苏 徐州 221116)

针对非合作通信系统中多径信道下含有大符号率偏差的M进制正交振幅调制信号定时载波的同步问题，提出了一种基于改进加德纳算法的M进制正交振幅调制信号定时载波联合同步方法．该方法首先利用加德纳算法中频偏与算法输出值之间的关系，进行定时偏移估计与载波偏移粗估计；然后利用与其相差半个码元的定时误差检测输出值的绝对值差进行锁定；最后利用锁相环跟踪细微的频偏和相偏．仿真结果表明，在多径信道下，所提的定时偏移和载波偏移的联合估计方法具有良好的估计性能．

同步;符号定时;频率偏移;联合估计;非合作通信

定时和频偏同步是数字通信系统中不可缺少的组成部分，也是数字通信系统解调的关键技术之一[1]．在非合作通信系统中，由于载波频率和符号率均未知，则估计值与实际值之间存在较大偏差，这就需要具有较大频偏估计范围与符号率调整范围的同步方法消除这些偏差，并选取最佳采样点以减小误码率[2]．因此，含有大符号率偏差的信号同步问题是解决非合作通信系统中信号解调的关键问题之一．一般来说，频偏与相位抖动对符号定时同步有一定影响，符号率偏差的存在也会对频偏估计有较大影响，并且频偏和定时分别进行同步会产生收敛时间变长、计算复杂度高等缺点，加上多径信道下符号间干扰和频率选择性衰落，将严重影响信号的同步性能．

由于非合作通信系统中接收端没有任何先验信息，则需要采用非辅助数据的同步技术．非辅助数据的定时频偏的联合同步方法可大致分为3种方法: 基于信号的循环平稳特性的联合同步方法[3-4]，但该方法仅仅对小频偏有效，且还需知道成形滤波器的冲击响应，况且估计性能较差; 基于边带定时恢复的联合同步方法[5]，但是该方法需要等效冲击响应为实数，且未考虑信号的特性对方法的影响;基于非线性变换的联合同步方法[6]，但是该方法存在频偏估计范围有限、未考虑多径信道影响的缺陷．此外，以上这些方法均未考虑符号率估计误差对同步性能的影响，因此，不能适合用于实际的非合作通信系统．

针对以上这些问题，笔者提出一种多径衰落信道下基于改进加德纳算法的M进制正交振幅调制(M-ary Quadrature Amplitude Modulation， MQAM)定时载波联合盲同步方法．该方法首先在加德纳算法进行定时的同时，利用其误差输出值的幅度粗估计频偏．在此过程中，用符号率偏差搜捕方法可将符号率偏差调整范围由0.5%扩大到10%，再利用与原算法相差半个码元的绝对值差进行锁定．最后用改进的极性判决锁相环跟踪．仿真结果表明，在多径衰落信道下，该方法性能更优．

1 定时载波联合同步系统模型

文中采用如图1所示的非合作通信系统的定时载波联合同步系统模型，其中r(mTs)是接收信号，首先经盲源分离、滤波及下变频等预处理，然后以估计出的符号率的四倍进行采样后的基带信号，即Ts为符号周期估计值的 1/4;x(mTs)是经初步频偏补偿和匹配滤波后信号;z(nT)是定时同步抽取后的信号;o(nT)是经锁相环跟踪细微频偏和相偏后的输出信号．文中联合同步方法是在该模型下实现的，其中各个模块的具体算法在以下各节进行详细说明．

图1 定时载波联合同步系统模型图2 加德纳算法定时恢复环路图

2 定时载波联合同步方法

2.1 频偏捕获及定时同步

加德纳算法[7]的优点是每个符号只需要两个采样点，易于全数字实现，并且可以和载波跟踪模块分开设计，所以该算法得到了广泛的应用．传统的加德纳算法采用两倍符号率的采样，但考虑到算法复杂度及性能，所以选取抽头数为4的Farrow结构滤波器，这就需要4倍符号率的采样．因此，文中采用的联合同步系统的过采样率仍为4，并未增加．此外，文献[8]证明了加德纳算法可应用到MQAM调制方式中，该算法的环路模块如图2所示．图2中的定时误差检测模块表达式为

ut(r)=yI(r-1/2) [yI(r)-yI(r-1)]+yQ(r-1/2) [yQ(r)-yQ(r-1)] ,

(1)

其中，yI(·)和yQ(·)分别表示信号y(t)在I支路和Q支路上的采样值，r表示符号数．当信号存在相位误差，即y(t)=x(t) exp(jΔθ) 时，代入式(1)，可得

ut(r)=xI(r-1/2) [xI(r)-xI(r-1)]+xQ(r-1/2) [xQ(r)-xQ(r-1)] ．

(2)

由式(2)可见，加德纳算法不受相偏的影响．当信号存在频偏，即y(t)=x(t) exp(j2πΔft)时，有

将式(3)和式(4)代入式(1)，可得

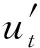
(5)

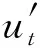
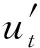
(6)

对加德纳算法表达式取期望，即Ut(r)=E[ut(r)]，则

Ut(r)offset=Ut(r)idemtocos(πΔfT) ,

(7)

其中，Ut(r)offset表示加入频偏后的误差均值，Ut(r)idemto表示无频偏情况下的误差均值．若将Δf也作为变量，则可将Ut(r)idemto表示为Ut(r，0)，将Ut(r)offset表示为Ut(r，Δf)．同时，也可用ut(r，Δf)表示将输入信号经Δf频率变换后再按加德纳算法表达式计算输出，则可得ut(r)即为ut(r，0)．

以上分析均是在理想情况下进行的，当具有滤波器和多径时，其性能会存在一定的衰减问题，但是以上推导结果表明了Ut(r，Δf)与频偏存在一定的变化关系和周期性．文献[9]方法是根据已知Ut(r，Δf)对Δf的变化曲线做拟合，再利用求Ut(r)offset的值判断其在曲线上的位置，对频偏进行粗估计．但在非合作系统中，由于成形滤波器系数、信道频率响应和信道衰减均未知，所以变化曲线不固定，频偏估计值不准确．若利用对Δf搜索，选取最大值，则复杂度太高．针对上述问题，基于过 1/(2T) 频率零点转换特性，将求最大值问题转为求零点问题，以便于准确定位频偏值，并且可与定时同步一起进行．由于利用相同的算法，故可设计为同一模块．也就是说，当 Δf=0 时，Ut(r，Δf+ 1/(2T))=0; 当 Δf>0 时，Ut(r，Δf+ 1/(2T))<0; 当 Δf<0 时，Ut(r，Δf+ 1/(2T))>0．由此可以迭代调整频偏大小，其估计范围可达 (-1/T，1/T)，超过了一个符号率，即涵盖了抽取信号的最大频偏，并且由于频偏估计与定时同时进行，可消除符号率偏移对频偏估计的影响，将频偏控制在小范围内，不使其严重影响加德纳算法的性能．为了扩大可调整的符号率偏差范围，可以根据文献[10]提出的符号率偏差搜捕方法，捕获10%的符号率偏差．

2.2 多径信道下联合同步方法的改进

由式(3)～式(7)可知，Ut(r)offset与无频偏情况下的x(t)经定时误差检测器(Timing Error Detector， TED)算法输出值Ut(r)idemto成正比关系．但估计Δf时，不需要用到Ut(r)idemto的具体值，而x(t)经多径信道后只对Ut(r)idemto部分的幅度值有影响，cos(πΔfT) 部分不变．因此，文中提出的频偏估计算法是适用于多径信道的．但是，定时同步环节的加德纳算法仍只适用于高斯信道和平坦衰落信道，则需要对其进行改进．文献[11]曾利用与加德纳算法相差半个码元的计算式，提出一种绝对值均值差运算来进行定时锁定检测，其原理如下:

由文献[11]可知，|wt(r)|对|ut(r)|存在翻转现象，以致于d(r)≠0．当 Δτ=0 时，d(r)可以取到最大值，其中 Δτ=τ-τ0，τ为定时误差估计值，τ0为实际的定时误差．在文献[11]中，以d(r)超过门限并持续一段时间作为锁定，但其门限受信号类型和信道衰落程度影响很大，在非合作通信系统中门限是无法确定的．因此，需要选取其他的方法来提取可使d(r)达到最大的τ值．从式(1)、式(7)和式(8)中可以看出

由其连续性和对称性可知，d(r+1/4)应该为零，即当Δτ=0时，d(r+1/4)=0; 当Δτ>0时，d(r+1/4)<0; 当 Δτ<0 时，d(r+1/4)>0，这样就可以迭代计算τ0值，并且此方法可适用于多径信道条件．综上所述，文中提出的多径衰落信道下联合方法实现框图如图3所示．

图3 多径信道下联合同步方法框图

在图3中，插值滤波器选用抽头数为4的Farrow结构，其对输入信号操作可表示为

(11)

其中，mk为内插基点，uk为分数间隔，即实际采样时刻与正确采样时刻之间的间隔，并且 0≤uk<1．环路滤波器表达式为

y(n)=y(n-1)+c1[x(n)-x(n-1)]+c2x(n) ,

(12)

其中，c1，c2为环路增益系数，其值由式(13)进行确定．

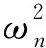
(13)

其中，ωn为环路带宽，ξ为阻尼系数，f为采样频率，K为环路增益．这里取ξ= 21/2/2，f=1，初始带宽ωn= 0.1．控制器即为数控振荡器和分数间隔器，输出作为插值滤波器参数．mk对应Ts采样整数点位置，uk对应Ts采样小数点位置．锁定检测部分d(r+1/4) 计算式为

d(r+1/4)=E[|ut(r+1/4)|-|wt(r+1/4)|]=E[|ut(r+1/4)|-|ut(r+3/4)|] ．

(14)

2.3 频偏和相位的跟踪

在未知调制方式的情况下，不能直接判决进行鉴相．为了较好地实现频偏和相位的跟踪与适用于星座点较密集的高阶正交振幅调制(Quadrature Amplitude Modulation，QAM)信号，文中采用了自适应门限的极性判决锁相环路，其框图如图4所示，其原理表达式为

其中，θ(n)为n时刻接收信号与其所在象限对角线之间的夹角，该夹角的变化范围为θ∈ (-π/4，π/4)．由于信号的星座图未知，所以选取门限时无法取固定值点．文中从平均能量的 2/3 处作为初始门限，以最大能量的 4/5 处作为最终门限，以一定比例逐渐增长作为门限值，超过门限的用式(10)进行鉴相，不超过的鉴相器输出则为零．

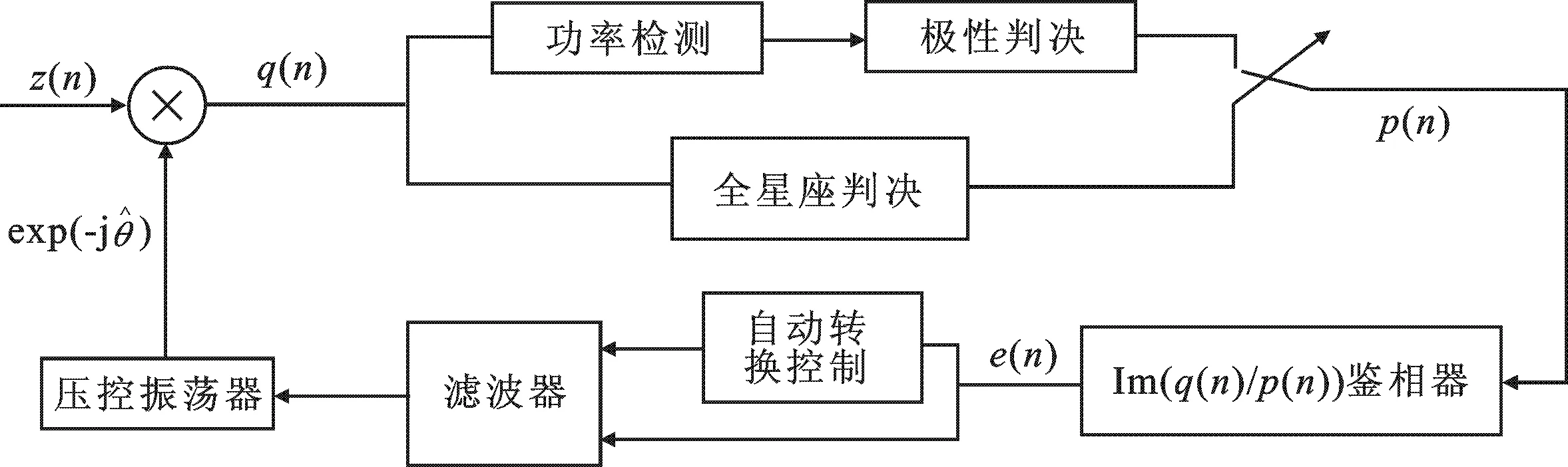
图4 自适应门限极性判决锁相环路图

3 仿真结果及分析

为了验证文中所提方法的有效性，通过MATLAB软件进行仿真实验．实验所采用的信号为MQAM信号，符号率为 50 Mbit/s，频偏值为 15 MHz，采用具有六径的步行环境测试信道ITU-A类信道[12]，延时为 {0 ns，310 ns，710 ns，1 090 ns，1 730 ns，2 510 ns}，功率衰减为 {0.0 dB，-1.0 dB，-9.0 dB，-10.0 dB，-15.0 dB，-20.0 dB} 的多径信道．仿真实验中在每个信噪比下进行 1 000 次蒙特卡罗试验，采用均方误差(Mean Square Error， MSE)评估文中方法的估计性能，其定义为

(16)

图5和图6是文中方法与现有方法在定时同步和载波同步下的对比性能曲线．从图5和图6中可以看出，随着信噪比的增加，定时偏移的估计性能和载波频率偏移的估计性能越来越好．文中方法的性能在整个信噪比的范围内优于文献[6]方法的性能，特别地，在低信噪比条件下，文中方法性能更优．

图5 不同定时同步方法的性能对比曲线图6 不同载波同步方法的性能对比曲线

4 结 论

文中提出一种非合作通信系统中MQAM信号定时载波联合同步方法，该方法利用加德纳算法中频偏与算法输出值之间的关系和与其相差半个码元的定时误差检测输出值之间的关系，并利用锁相环跟踪细微的频偏和相偏．仿真结果表明，在多径衰落信道下，文中方法比现有方法的性能更优．

参考文献：

[1] LIN T C, PHOONG S M. A New Cyclic-prefix Based Algorithm for Blind CFO Estimation in OFDM Systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(6): 3995-4008.

[2] GAPPMAIR W, SCHLEMMER H, GINESI A. Joint Synchronization of Symbol Timing and Carrier Frequency Using the Extended Zero-crossing Property[C]//Proceedings of the 2016 8th Advanced Satellite Multimedia Systems Conference and 14th Signal Processing for Space Communications Workshop. Piscataway: IEEE, 2016: 7601537.

[3] ZHANG X, HU J H. A New Time Delay Estimation Algorithm for Mixed OFDM Signal[C]//Proceedings of the 2015 International Conference on Wireless Communications and Signal Processing. Piscataway: IEEE, 2015: 7341146.

[4] 吴涛, 戴旭初. 频率偏移和符号定时误差的盲估计方法[J]. 数据采集与处理, 2005, 20(3): 291-296.

WU Tao, DAI Xuchu. Blind Estimation of Frequency Offset and Symbol Timing Error[J]. Journal of Data Acquisition & Processing, 2005, 20(3): 291-296.

[5] 项立, 钟绍波. 单载波无线系统载频与定时偏移估计算法[J]. 计算机应用与软件, 2010, 27(5): 98-101.

XIANG Li, ZHONG Shaobo. Carrier Frequency and Timing Offsets Estimation Algorithm for Single Carrier Wireless Systems[J]. Computer Applications and Software, 2010, 27(5): 98-101.

[6] 许小东. 非协作数字通信系统盲解调关键技术研究[D]. 合肥: 中国科学技术大学, 2007.

[7] GAPPMAIR W, KOUDELKA O. Blind Symbol Timing Recovery in the Presence of IQ Mismatch and DC Offset[C]//Proceedings of the 2014 9th International Symposium on Communication Systems. Piscataway: IEEE, 2014: 1133-1138.

[8] CHEN L M, LIANG Y, WAN G J. Symbol Timing and Carrier Frequency United Estimation for MPSK Signals[C]//Proceedings of the 2010 International Conference on Computer Application and System Modeling. Piscataway: IEEE, 2010: 5610-5613.

[9] 史晓峰, 陈咏恩. DVB-C接收机中的时钟恢复电路设计[J]. 计算机工程与应用, 2006, 42(33): 78-80.

SHI Xiaofeng, CHEN Yongen. Design of Timing Recovery Loop for DVB-C Receiver[J]. Computer Engineering and Applications, 2006, 42(33): 78-80.

[10] ZHANG S, XU L, YU J, et al. Dual-stage Cascaded Frequency Offset Estimation for Digital Coherent Receivers[J]. IEEE Photonics Technology Letters, 2010, 22(6): 401-403.

[11] LOU H, LIN P F. A New Lock Detector for Gardner’s Timing Recovery Method[J]. IEEE Transcations on Consumer Electronics, 2008, 54(2): 349-352.

[12] ITU. Guidelines for Evaluation of Radio Transmission Technologies for IMT-2000: Recommendation ITU-R M.1225[S]. Geneva: ITU, 2010.

JointcarriersynchronizationandsymboltimingforMQAMinnon-cooperationcommunicationsystems

LIUMingqian1,2,3，CHENQian2，WUYun3，LIBingbing1

(1. Collaborative Innovation Center of Information Sensing and Understanding, Xidian Univ., Xi’an 710071, China; 2. School of Electronic and Optical Engineering, Nanjing Univ. of Science and Technology, Nanjing 210094, China; 3. Xuzhou LEO Medical Equipments Co., Ltd., Xuzhou 221116, China)

Aiming at the problem of symbol timing and carrier synchronization of (M-ary Quadrature Amplitude Modulation) MQAM signals with large symbol rate deviation in non-cooperative communication systems under multipath channels,a new method based on the improved Gardner algorithm for MQAM signal timing carrier joint synchronization is proposed. First, the method obtains timing offset estimation and carrier offset coarse estimation using the relationship between frequency offset and output value of the Gardner algorithm. Then, locking is performed with the difference of the absolute value between estimation and the output value of timing error detection which is half a symbol different from the estimation. Finally, the method uses the phase-locked loop to track the fine frequency offset and phase offset. Simulation result shows that the proposed joint estimation method of timing offset and carrier offset has a good estimation performance under the condition of multipath channels.

synchronization; symbol timing; carrier frequency offset; joint estimation; non-cooperation communication

2017-01-04

时间：2017-06-29

国家自然科学基金资助项目(61501348，61271299)；陕西省自然科学基础研究计划资助项目(2016JQ6039)；国家博士后科学基金资助项目(2017M611912)；高等学校学科创新引智计划资助项目(B08038)；江苏省博士后科研资助计划资助项目(1701059B)

刘明骞(1982-)，男，讲师，博士，E-mail: mqliu@mail.xidian.edu.cn．

http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1734.008.html

10.3969/j.issn.1001-2400.2018.01.004

TN911.7

A

1001-2400(2018)01-0017-06

(编辑： 李恩科)