门座式起重机大拉杆的横向风振

董胜龙

(中船第九设计研究院工程有限公司， 上海 200063)

1 大拉杆横向风振现象

某船厂门座式起重机在5级风状态下工作时，大拉杆经常出现振动，带动整机振动，当转动起重机使大拉杆接近顺风时，振动基本消失，一旦大拉杆横向处于逆风状态时，振动就会出现。

对于船厂门座式起重机大拉杆出现横向风振现象，有必要进行分析与研究，解决工程实际问题，并指导设计。图1为S4565K12型45 t门座式起重机的示例。

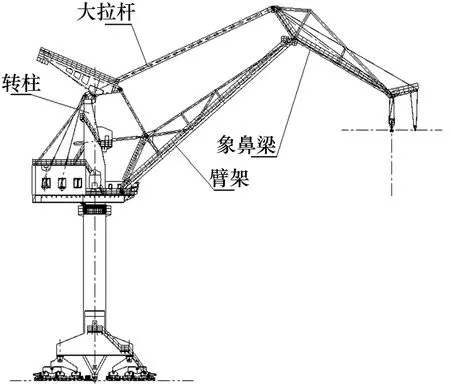
图1 S4565K12型45 t门座式起重机示例

2 大拉杆结构及受力分析

图2为S4565K12型45 t门座式起重机的大拉杆结构介绍，大拉杆是采用材料为Q345的10 mm板材焊接成箱形截面的梁，两端通过铰轴连接，形成两端铰接状态，其结构参数如表1所示。

图2 大拉杆结构

序号名称参数1两端铰轴中心长L/mm410302截面上下板宽b/mm6003截面左右板高c/mm8004截面上下板厚/mm105截面左右板厚/mm106大拉杆重量M/kg110007截面绕水平轴惯性矩I/mm42821733333

由图1门座式起重机的示例可看出，大拉杆一端安装在转柱顶部的铰轴上，另一端与象鼻梁的铰轴联接。由此可见，大拉杆承受臂架、象鼻梁(包括吊重)产生的拉力，以及自身的重量，同时承受风的作用力，在分析时忽略铰轴的摩擦力。

大拉杆横截面尺寸如图3所示。

图3 大拉杆横截面尺寸

大拉杆横截面力学特性如下。横截面积：A=28 000 mm2，绕水平轴截面惯性矩：I=2 821 733 333.333 4 mm4。

大拉杆的柔度(长细比)λ为

λ=μL/i(1)

式中：μ为压杆的长度系数；L为大拉杆的长度，L=41 030 mm；i为惯性半径，i=(I/A)0.5= 317.452 658 6 mm，其中绕水平轴截面惯性矩I=2 821 733 333 mm4，截面面积A=28 000 mm2，因此，当绕水平轴截面惯性矩I=2 821 733 333.333 4 mm4时，λ=129.25。

大拉杆自振频率f的理论计算及有限元模态分析如下：

f=ω/2π(2)

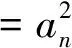
采用有限元进行模态分析，得到开孔大拉杆横向振动的自振频率f=1.402 605 Hz。大拉杆有限元模型如图4所示，大拉杆横向振动第一阶振动模态及频率如图5所示。

图4 大拉杆有限元模型

图5 大拉杆横向振动第一阶振动模态及频率

3 大拉杆横向风振分析

3.1 涡激振动

根据卡门涡列的形成，当风垂直于大拉杆作用时，在大拉杆两侧、背后产生交替的旋涡，且将由一侧向另一侧交替脱落，这就是卡门涡列现象。

这种涡列的产生使大拉杆上下面的压力出现周期性变化，大拉杆上面的压力减小，下面的压力增大，因此在大拉杆上形成的一个向上的横向力，随着旋涡脱落交替出现，这个向上的横向力也交替出现。向上的横向力迫使大拉杆产生横向振动，这种由卡门涡流引起的与风向垂直的振动，就称为涡激振动。

一般情况下，其振动表现为强迫振动，但若振动加强，则会产生由振动控制的涡流，这部分形成自激振动。所以，涡激振动存在2种特性：强迫振动和自激振动。

当大拉杆的自振频率接近旋涡脱落频率，产生涡激共振，此时形成锁定，即大拉杆的自振频率控制了旋涡脱落频率。

由Strouhal number可知：

St=ns×D/v(4)

式中：ns为旋涡脱落1个完整的频率，Hz；D为大拉杆垂直于风速平面上的外形尺寸，D=0.82 m；v为风的平均速度，m/s。

由(4)式可得

ns=St×v/D(5)

不同风力和风速的旋涡脱落频率计算如表2所示。

表2 同风力和风速的旋涡脱落频率计算结果

由式(5)可知，若结构的横截面形状和尺寸确定，则St和D确定，决定旋涡脱落频率ns的因素就是风速v。而大拉杆的自振频率f可通过公式或有限元方法得到。目前的大拉杆横向振动第一阶的自振频率：不开孔大拉杆，f=1.434 86 Hz；开孔大拉杆，f=1.402 605 Hz。由此可见，具有形成涡激共振的条件。

若在大拉杆迎风面上开孔，一部分气流将直接穿过孔口，那么在孔口周围就无法形成较大的周期性旋涡。

在迎风面上开孔后，迎风面上的阻力将显著减小，而横向升力则变化不大。由于改变了旋涡周期脱落条件，涡激共振可能性将显著减少。但是在没有孔口的大拉杆结构中仍然还会存在涡激振动，有形成涡激共振的可能性。

3.2 驰振和颤振

目前，在理论上，对驰振、颤振的机理还正处于探讨和研究之中。

当风垂直于大拉杆作用时，在大拉杆结构前缘处产生气流分离，在侧面形成分离剪切层，分离剪切层较强的夹持使侧面流动的气流逐步陷入分离剪切层中，从而在侧面与分离剪切层之间形成负压分布区，使结构整体受到与运动方向一致的气动升力，该气动升力会起到正的或负的阻尼作用效果，气动阻尼力是风与结构耦合作用的结果。

驰振和颤振是在结构物受风上侧断面边缘放出的前缘分离涡流而引起的横向风振动。横向风弯曲单自由度振动称为驰振，而弯曲和扭转的两自由度振动称为颤振。

驰振是一种失稳形式的振动，驰振一旦发生，便成为剧烈的振动，有导致结构破坏的危险性。因此，对大拉杆在驰振上是否稳定的判断就十分重要。

根据驰振理论，大拉杆结构振动体系稳定的Den Hartog判别式：振动体系净阻尼系数d>0时，大拉杆是稳定的振动；d<0时，大拉杆是失稳式的振动。

当d>0时，大拉杆的振动将衰减；当d<0时，大拉杆的振动加剧。当驰振出现时，总阻尼必须小于零，因此，容易发生驰振的将是质量和阻尼比较小的钢结构，同时驰振也与横截面有关。因结构体系的振动而使作用于其上的空气力发生变化并且使振动加剧的现象称为驰振。

振动体系净阻尼系数d由2部分组成：一是机械阻尼，二是气动阻尼。

当大拉杆迎风面开孔后，由于迎风面上的阻力减小，而产生驰振的激励力却有所增大，由单自由度体系的运动方程可以判断：当激励力增加，而质量、阻尼、刚度没有变化时，为保持等式两边平衡，振动将加大，这将增大产生驰振的可能性。

对振动体系净阻尼系数d进行计算，当d=23.62>0时，大拉杆的振动体系是稳定的，驰振不会发生。

3.3 随机振动

当气流的雷诺数处于1×105≤Re<3.5×106时，气流分离点前是层流，在尾流中层流向湍流过渡，当Re较低时，过渡在结构体较远的下游处，随Re的增加，过渡逐渐趋于结构体表面。在这一范围，结构体尾流在分离后主要表现为湍流尾流，尾流中出现比较随机的旋涡脱落。

当风力达到5级时，Re=69 000vD，式中：风速v=7.7 m/s；特征尺寸D=0.82 m，则Re=4.36×105。

因此，在大拉杆背后的湍流尾流将引起横向风的随机振动。

4 大拉杆横向风振结论

结论1：

(1) 没有通风孔的大拉杆，在风速达到7.5 m/s时将产生涡激共振。

(2) 当大拉杆开有通风孔后，涡激共振可能性将显著减少。

(3) 但由于开孔大拉杆横向振动第一阶的自振频率f=1.402 605 Hz，与风速7.7 m/s旋涡脱落频率ns十分接近，有可能符合产生涡激共振的条件，在各方因素具备时，可能出现涡激共振。在没有孔口的结构部分还会存在涡激振动，也有可能形成涡激共振。

结论2：

大拉杆一般不会产生驰振。

结论3：

大拉杆将产生随机振动，而随机振动一直存在。当随机振动的频率与大拉杆横向振动第一阶的自振频率f=1.402 605 Hz接近时，产生共振。

综上所述，大拉杆横向风振由随机振动、涡激振动组成。主要存在4种振态：

(1) 仅随机振动状态，非共振条件下，振动可接受。

(2) 随机振动+涡激振动状态，非共振条件下，振动也可接受。

(3) 随机振动的共振状态+涡激振动，特定条件下，如风向、风速在一定时间内基本恒定，大拉杆恰好与风向处于适当位置、角度，且随机振动频率与大拉杆横向振动第一阶的自振频率接近，将可能会产生随机振动共振状态，不过其概率很小。

(4) 涡激振动的共振状态+随机振动，特定条件下，如风向、风速在一定时间内基本恒定，大拉杆恰好与风向处于适当位置、角度，且旋涡脱落频率与大拉杆横向振动第一阶的自振频率接近，有可能形成涡激共振。不过其概率也很小。

因此，大拉杆有害横向风振主要是：随机振动的共振状态+涡激振动，涡激振动的共振状态+随机振动。

5 消除或减弱大拉杆横向风振的基本原则和措施

5.1 基本原则

(1) 提高大拉杆自振频率并保证较大的大拉杆刚度。

大拉杆自振频率越高，形成随机振动共振状态的风速越大，而风速越大，则越不稳定，因此就不易形成随机振动。

大拉杆自振频率越高，相同旋涡脱落频率所需的风速就越大，即产生涡激共振的临界风速就越大；而风速越大，则越不稳定，因此就不易形成涡激振动。

大拉杆自振频率越高，则振动体系净阻尼系数d中的机械阻尼就越大，驰振的可能性就越小。

可以采用提高大拉杆刚度、控制结构质量增加的方法，提高大拉杆自振频率。由运动方程可知：结构刚度越大，振动位移幅值就越小。即使振动，由于刚度大，其振动位移幅值可控制在可接受的范围内。

(2) 改变气流通过大拉杆的形态。

通过改变气流通过大拉杆的形态，破坏卡门涡列形成的条件，使涡激共振可能性显著减少。

(3) 增加大拉杆的阻尼。

当大拉杆阻尼越大，则振动体系净阻尼系数d中的机械阻尼也就越大，驰振的可能性就越小。

其次，阻尼越大，由运动方程可知：振动位移和速度幅值就越小。

(4) 控制截面高宽比。

为使振动体系净阻尼系数d中的气动阻尼尽量大于零，箱形截面的高宽比为0.50～0.75较为合适。

5.2 措施

(1) 提高大拉杆自振频率，提高惯性矩。

由式(3)可知，要提高大拉杆自振频率，主要提高绕水平轴截面惯性矩I。

当I由0.002 82 m4提高到0.009 27 m4时，大拉杆自振频率f由1.373 9 Hz提高到2.490 9 Hz，而柔度λ由129.25降低到82.07。此时，涡激共振的临界风速大于13.6 m/s。结构调整后的大拉杆有限元模型与结构调整后大拉杆横向振动第一阶振动模态及频率如图6和图7所示。

图7 结构调整后的大拉杆横向振动第一阶振动模态及频率

图6 结构调整后的大拉杆有限元模型

当I=0.009 27 m4时，振动体系净阻尼系数d提高到41.95，驰振的可能性就更小。

(2) 保证较大的大拉杆刚度。

原大拉杆刚度：160/41 030 mm=1/256.4 mm，刚度较低，在低风速下，易产生共振，且振动幅值较大。自重状态下，大拉杆横向变形云图如图8所示。

图8 大拉杆横向变形云图

大拉杆刚度的增加：51/41 030 mm=1/804.5 mm，刚度较高，在低风速下，不易产生共振，且振动幅值相比原刚度状态下较小。结构调整后自重状态下，大拉杆横向变形云图如图9所示。

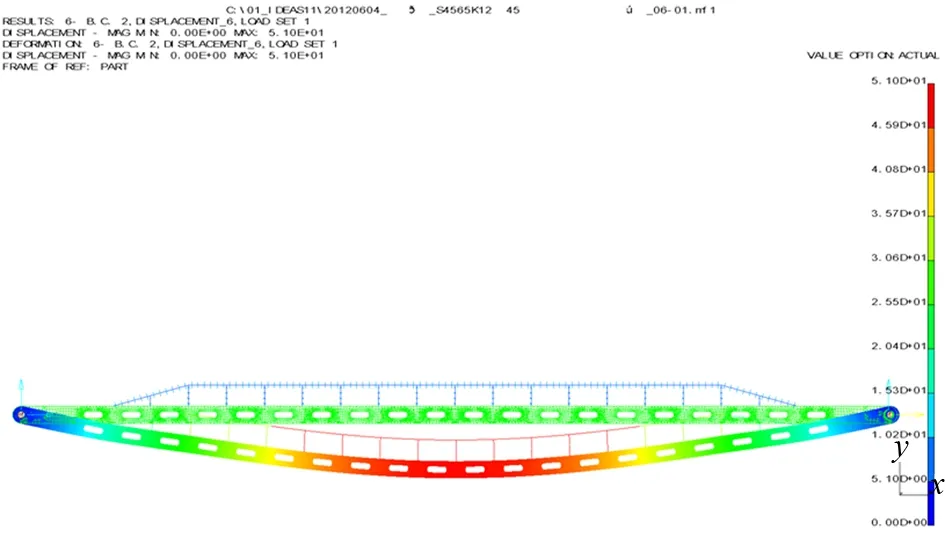
图9 结构调整后的大拉杆横向变形云图

(3) 改变气流通过大拉杆的形态。

方法一：

在大拉杆迎风面上开孔是一个很好的方法，这样一部分气流将直接穿过孔口，那么在孔口周围，就不能形成较大的周期性旋涡。迎风面上的阻力将显著减小，而横向升力则变化不大。由于改变了旋涡周期脱落条件，涡激共振可能性将显著减小。

方法二：

一是在大拉杆上、下表面分别设置斜向导流板，上、下表面的斜向导流板呈交叉状，以改变气流的形态。

二是在大拉杆迎风面、背风面中心位置布置水平导流板，以改变旋涡周期脱落条件。

最后，该船厂的门座式起重机上的大拉杆按照本文的方法和措施消除了横向风振，目前使用良好。

[1] 黄本才，汪丛均.结构抗风分析原理及应用[M].2版.上海：同济大学出版社，2008.