艉轴承设计间隙对轴承油膜刚度系数的影响

温小飞， 陈班班， 沈学敏， 崔志刚

(1．浙江海洋大学 港航与交通运输工程学院， 浙江 舟山 316022； 2.武汉理工大学 能源与动力工程学院， 湖北 武汉 430070； 3.舟山市船舶检验处， 浙江 舟山 316000)

0 引 言

大型船舶艉轴承一般采用径向滑动轴承的油润滑为主，滑动轴承油膜特性参数是影响轴系动力学的关键因素之一，对船舶航行起着至关重要的作用[1]，因此，国内外学者均对此展开研究。朱汉华等[2]研究轴承在油膜力动态耦合作用下质量偏心对轴系的影响；杨守平等[3]建立某V8增压柴油机曲轴轴系动力学与轴承油膜动力润滑耦合仿真模型,求解获得轴承载荷、轴心轨迹、最小油膜厚度、最大油膜压力、摩擦功耗等参数。张艾萍等[4]根据N-S方程采用CFD软件计算分析滑动轴承间隙对转子的稳定性影响。MANSHOOR等[5]通过轴承长细比的不同，应用三维CFD分析，研究不同湍流模型在轴承系统润滑油膜的影响。SMOLIK等[6]研究径向轴承间隙对涡轮增压器转子动力响应的影响。考虑船舶艉轴承设计间隙油膜刚度系数的影响，根据Reynolds方程Sommerfeld边界条件，应用有限长轴承数学模型进行化简,以艉轴承的设计间隙为变量，研究不同转速条件下船舶轴系轴承刚度系数变化规律。

1 滑动轴承的油膜形成机理

滑动轴承在旋转过程中轴颈、轴瓦之间形成收敛的楔形空间，该空间内充满黏性的流体，并形成稳定压力场，当压力场合力超过重力时便将轴径抬起，即轴承和轴颈之间形成油膜[7]。该过程如图1所示，设轴径以角速度Ω旋转，由于受外载荷W的作用，轴承中心O1和轴颈中心O产生偏心，使得轴承和轴颈之间形成收敛楔和发散楔，当轴颈旋转带动润滑油从发散区域到收敛区域，沿轴颈旋转方向的间隙由大变小，形成油楔，使得润滑油内产生压力，形成油膜。当油膜压力大于重力时，轴颈中心O和轴承中心O1的偏差变大，此时通过轴颈中心O建立xOy坐标系。在轴承保持动态平衡时可以分析出力的关系。其中，Fe和Fφ分别为作用于轴颈的非线性油膜力的径向和切向分量，Fx和Fy分别为作用于轴颈的非线性油膜力在x和y轴负方向的分量。此外，R为轴承半径，r为轴颈半径，φ是从延长线(偏位线)顺时针方向转至油膜位置的角度，一般称之为偏位角。

图1 滑动轴承结构示例

2 轴承油膜刚度系数的求解方程

轴承油膜刚度系数的求解方程源于有限长轴承的Reynolds方程，首先通过对轴承油膜压力场的求解得到油膜力，再施加微小位移扰动量从而推导出油膜刚度系数公式。

径向滑动轴承有限长轴承Reynolds方程式[8]为

式中：p为油膜压力；μ为黏度系数；Vr为切向速度；θ为偏位角；Ω为旋转角速度；z为轴承纵坐标；h为油膜厚度，h=c(1+cosθ)。

应用Reynolds边界条件经积分求解可得油膜压力分布p(θ,z)，求解出油膜压力的具体分布规律，如图2所示。图2中不同的长度下油膜压力在角度100°～180°之间符合正态分布，且随角度增加而增加，在约18°时达到峰值，最终趋于平稳。

图2 无量纲压力分布云图

在获取油膜压力分布云图的情况下，通过油膜压力分布云图可进一步推导出油膜力公式为

(2)

式中：p为油膜压力；L为轴承长度；θ为偏位角；z为轴承纵坐标。

将Fe和Fφ分量从柱坐标变化为xOy坐标系，则油膜力的水平分量Fx和垂直分量Fy为

(3)

式中：φ为偏位角。

在给定位移扰动时，轴颈上油膜反作用力会发生变化，力的变化和扰动量之间是非线性的，当扰动量为微小量时，可以进行线性化。将油膜给轴颈的反作用力对扰动参数作Taylor展开，保留一阶微量，可得

(4)

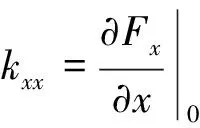
(5)

3 轴承设计间隙的影响分析

对式(1)和式(5)的传递关系和量纲进行分析，可得油膜间隙c和油膜力f的关系为

p∝f(h,μ,r2,Vr,z)(6)

又因h=c(1+ecosθ)，所以

h∝f(c,e)(7)

由式(4)可知：刚度系数Fx和Fy是线性函数。此外，油膜压力p可通过油膜压力云图得到。由式(5)可知：刚度系数与Fx和Fy具有一致性。因此，可以推出：

K∝f(μ,R2,L,c-1,ε2)(8)

对此，从理论分析可得艉轴承间隙和刚度系数具有相关性。为进一步研究两者的关系，采用实船模型建模并进行分析。

4 数值模拟与分析

4.1 几何模型

理论分析艉轴承设计间隙和油膜刚度系数的关联性，采用64 000 t散货船轴系进行建模、仿真和验证。实船的基本参数：船舶总长为199.90 m，垂线间长为194.5 m，型宽为32.26 m，型深为18.50 m，设计吃水为11.30 m，载重量为63 800 t，设计航速为14.00 kn，船舶主机额定功率为8 050 kW，额定转速为89.0 r/min。轴承、轴颈几何尺寸及长细比等计算参数如表1所示。

表1 船舶轴系轴承系统几何参数

船舶尾部结构、船舶主机、轴系等位置及其布置情况如图3所示。该船型采用单艉轴承支承形式，中间轴承与艉轴承之间的位置关系对船舶轴系轴承负荷分配具有显著影响。

图3 船舶尾部结构及主推进系统布置

4.2 仿真与分析

根据所述的目标船舶和表1轴系基本设计参数，运用油膜力几何模型以及相应边界条件，在船舶轴系轴承负荷数值计算结果的基础上，采用MATLAB编程计算正常运转范围(30～90 r/min)内0.30 mm，0.35 mm，0.40 mm，0.45 mm，0.50 mm等5个不同间隙条件对应的船舶轴系油膜刚度系数，整理计算结果得到稳态计算工况的船舶轴系各轴承油膜刚度系数-转速曲线。其中，以艉轴承、中间轴承和主机主轴承对应的油膜刚度系数-转速曲线作为要点进行讨论分析。

艉轴承模拟计算结果如图4所示，a),b),c)和d)中的油膜刚度系数曲线图形分别代表油膜等效刚度系数的4个分量：kxx,kyy,kxy,kyx。图4a)中：当设计间隙在0.35 mm和0.40 mm时，艉轴承刚度系数变化曲线在低速区发生波动，而艉轴承设计间隙在c=0.45 mm时在高速区刚度系数-转速曲线发生波动变化；当设计间隙为0.50 mm时，油膜刚度系数曲线在30～60 r/min和80～90 r/min之间发生变化。图4b)为艉轴承交叉刚度kyy的变化曲线图，可以得出：设计间隙为0.30 mm时，曲线变化平滑；设计间隙为0.35 mm和0.40 mm时，在转速为30～40 r/min时，油膜刚度系数kxy曲线发生变化，在转速为35 r/min之前随转速升高而降低，转速高于35 r/min后，曲线变化呈上升趋势，等效刚度曲线也随转速升高而变化，超过40 r/min时，曲线变化趋于平稳。可从图4c)和图4d)中得到与前2幅图相反的曲线变化规律。

图4 艉轴承油膜刚度系数变化曲线(变艉轴承设计间隙)

刚度系数曲线随着转速升高的变化趋势一致，随着艉轴承设计间隙的增加会导致刚度系数曲线的上下波动。在船舶轴系艉轴承设计间隙为0.30 mm时，船舶艉轴承油膜刚度系数与转速之间具有良好的线性关系，随着船舶轴系艉轴承设计间隙加大，其线性关系逐渐变差，当船舶轴系艉轴承设计间隙增大到0.50 mm时，船舶艉轴承油膜刚度系数-转速关系曲线呈现出强烈的波动性。在某一特定船舶艉轴承设计间隙范围内，船舶轴系艉轴承油膜刚度系数至少存在一个峰值点，且该峰值点位置与船舶艉轴承设计间隙大小有关。

为进一步分析船舶艉轴承设计间隙对轴系其他轴承刚度系数的影响，将中间轴承的刚度系数数据整理得到图5。从4幅刚度系数—速度曲线(kxx,kyy,kxy,kyx)变化图可看出：在不同的轴承油膜设计间隙中，刚度曲线随转速升高变化趋势相同，且均在c=0.50 mm的设计间隙中，在高转速区域内有较为微小的波动。

图5 中间轴承油膜刚度系数变化曲线(变艉轴承设计间隙)

主轴承的刚度曲线变化如图6所示。主机轴承的刚度变化曲线kxx,kyy,kxy具有良好的线性特征变化，轴承油膜刚度系数变化曲线并未出现如艉轴承油膜刚度曲线变化的峰值现象，且在具稳态工况的计算上数值相差较小。在kyx的刚度系数—速度变化曲线中，总体变化形势趋于一致，且在高转速区域内具有一定的波动。

图6 主轴承油膜刚度系数变化曲线(变艉轴承设计间隙)

5 结 论

(1) 船舶艉轴承设计间隙与油膜刚度系数之间具有一定的相关性。

(2) 船舶轴系轴承设计间隙对油膜刚度系数具有较大的影响，轴承刚度系数不同，其计算数值大小上有较大的差异，且油膜刚度系数曲线的线性关系变化不同。

(3) 船舶轴系艉轴承设计间隙变化对其本身轴承油膜刚度系数变化规律影响较大，而中间轴承油膜刚度系数的线性关系影响相对较小，特别是主轴承kyx的变化曲线在高速区域波动较大。

因此，选择和保持合适的船舶艉轴承的设计间隙值有助于保障船舶轴系运行的稳定性和安全性，同时应在船舶营运过程中重视船舶轴系轴承间隙检测和管理。

[1] 张智辉,王雪山. 艉轴架照光法环氧浇注安装的工艺[J]. 造船技术,2017(2):42-46.

[2] 朱汉华,严新平,刘正林,等. 油膜力耦合下质量偏心对船舶轴系振动的影响[J]. 船舶工程,2008(2):20-23.

[3] 杨守平,张付军,黄英,等. 内燃机曲轴系统动力学与动力润滑耦合仿真[J]. 车用发动机,2010(4):51-55.

[4] 张艾萍, 林圣强, 李雨娇. 滑动轴承间隙对转子稳定性的影响[J]. 汽轮机技术, 2013, 55(2):86-88.

[5] MANSHOOR B, JAAT M, IZZUDDIN Z, et al. CFD Analysis of Thin Film Lubricated Journal Bearing[J]. Procedia Engineering, 2013, 68(12):56-62.

[6] SMOLIK L, HAJŽMAN M, BYRTUS M. Investigation of bearing clearance effects in dynamics of turbochargers [J]. International Journal of Mechanical Sciences, 2016.

[7] 周桂如. 流体润滑理论[M]. 杭州：浙江大学出版社, 1990.

[8] 钟一谔，何衍宗. 转子动力学[M]. 王正，李方，译.北京：清华大学出版社, 1987.