主动学习策略融合算法在高光谱图像分类中的应用

崔颖，徐凯，陆忠军，刘述彬，王立国

（1. 哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2. 黑龙江省农业科学院遥感技术中心，黑龙江 哈尔滨 150086）

1 引言

高光谱图像分类已经成为高光谱图像的重要应用之一。对于高光谱图像分类，普通用户对其内容的判别是有难度的，通常需要一位专家或借助同一场景的高分辨率遥感图像来完成，这使图像分类中用于训练的样本比较有限，如何在较少的人工成本基础上，用最少的训练样本，最大限度地提高分类器性能成为图像分类的关键。

机器学习中的主动学习方法通过其优越的挑选策略，能够在极大地减少人工成本的同时，获取最有价值的样本进行标注，相较于随机标注而言，主动学习算法拥有无可比拟的优势[1]。在主动学习挑选策略方面，Mitra等[2]提出了基于边缘取样（MS）的主动学习方法，用于面向对象的多光谱遥感图像分割。为了解决多分类的问题，Joshi等[3]提出了基于多类别后验概率差异最小化的方法BvSB，该算法能够有效度量哪些样本对分类器边界影响最大。Tuia等[4]提出了基于熵值的熵值装袋（EQB）的主动学习算法，该算法独立于分类器，且在遥感数据集上表现出较好的性能，但 EQB会倾向于选择有较多预测类别数的样本，为了解决此问题，李宠等[5]提出了改进EQB算法的均值熵值装袋查询（aEQB）。

在半监督学习方面，Li等[6]提出了结合半监督的主动学习方法，将主动学习过程产生的价值样本用来加速分类器的训练，和伪标签一起辅助分类器进行高效的分类。Wan等[7]提出了基于主动学习的伪标签校验框架，极大地提高了半监督学习中伪标签的置信度，并在高光谱图像中得到验证。Wang等[8]借鉴文献[7]的框架，提出了主动学习与聚类相结合的伪标签校验的方法，进一步提高了伪标签的置信度。王立国等[9]将主动学习和差分算法进行结合，通过主动学习方法选取置信度较高的伪标记样本，并通过差分进化算法交叉变异伪标记样本扩充标记样本集，来提升模型分类性能。Samiappan等[10]提出了Co-Training与主动学习算法进行组合的半监督算法，缓解了 Self-Training中容易产生的数据倾斜问题而导致的分类器持续恶化的情况。王立国等[11]提出了使用Tri-Training和主动学习的边缘策略（MS）结合，解决了初始有标签样本数量较少导致分类器差异性能不足的问题。赵建华等[12]提出了基于投票熵改进的主动学习算法，能够减少主动学习过程中可能产生的孤立点和冗余点，再和半监督算法结合迭代，缩小了计算规模，提升了算法稳定性。

现在的方法大都是对单一策略进行衍生研究，或是对空间信息和光谱信息的联合组合[13]，没有考虑2种策略结合作为新的基础策略及进行之后的深度改造的方法。使用单一策略对样本多次采样时会出现抖动的现象，对于需要采样稳定的场景而言，采样存在标记风险，即更大程度浪费人力在标注非最优价值的样本。

本文借鉴集成学习中的模型权重组合，对主动学习2种基础策略进行融合，充分发挥多种主动学习策略在不同数据集和不同阶段的优势，减少挑选未标记样本过程中不同策略的抖动现象。实验表明，算法能够更快收敛，并可将抖动频率降低为原来的16.7%，人工耗费成本率降低最高至25.4%，极大降低人工标记成本，使整体策略在一定程度上达到基策略模型的最优。

2 基于策略融合的主动学习方法

基于策略融合的主动学习方法受集成学习的启发，进行主动学习的策略组合，将单一差异化模型组合加权成一个融合策略模型，以下将该算法简称为ESAL（ensemble strategy active learning）。

2.1 主动学习算法框架

主动学习算法主要分成2个部分：一部分是学习引擎，也就是分类器G；另一部分是抽样引擎Q，即如何选择价值样本。主动学习算法的意义在于使用策略在未标记样本集合中选择最有价值的实例，将其交给专家S进行标注，然后将标记样本增加到下一次迭代的训练集T中，使分类器进行迭代训练。典型的主动学习的迭代框架如图1所示。

2.1.1 aEQB策略

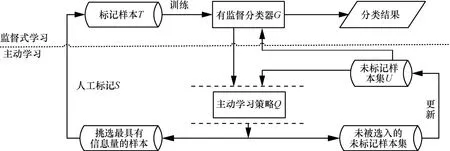
图1 典型的主动学习的迭代框架

主动学习算法中的一个分支是基于委员会策略算法，其过程可分为如下几步。首先将原始训练集分为K个子训练集，每个训练集都是由装袋方法进行挑选出样本。然后，每个训练集都被用于模型的训练，并对未标记样本池中的样本进行类别预测，对每个样本xi∈U，都有K个标签，便可以计算出样本xi标记类别ω的概率，该概率可用来评估未标记样本的xi类不确定度，样本的熵值计算如式(1)所示[4]。

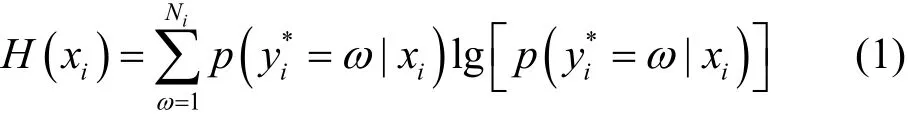
其中，是第i个样本所判断的标签类，是样本xi的预测类别为ω的概率。

熵越大，则表明分类器对此样本的分类存在更大的不确定性，选择具有最大信息熵的样本作为最有价值的样本让专家进行标注，然后再添加到现有的训练样本中进行下一次迭代训练。但有研究者[14]发现，在多分类问题上，熵有时并不能代表样本的不确定度，有时较小熵的样本分类不确定度会高于熵稍大的样本。韩松来等[15]从理论方面证明了信息熵具有多值偏向问题，即分类器的训练迭代预判过程中，会更关注于复杂的样本而忽视较少预测类别数的样本区域，这会导致之后加入的训练样本类别分布不均，产生数据倾斜问题。李宠等[5]借鉴Quinlan等[16]提出的信息增益比率度量方法，提出了均值装袋查询（aEQB），通过加入一个分类信息的项来惩罚多值属性，aEQB的描述如式(2)所示[5]。

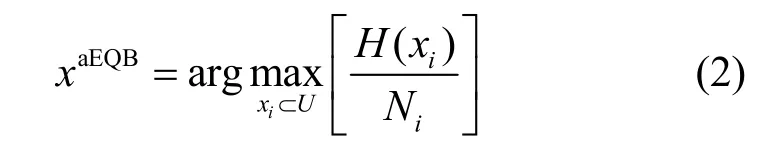
其中，H(xi)是式(1)中的样本信息熵，Ni是委员会成员预测样本xi的类别总数，满足1 ≤Ni≤N，N是所有类别数目。

2.1.2 BvSB策略

主动学习的另一个比较常用的策略是基于边缘的主动学习算法，基本思想是从每次未标记样本池中挑选出最靠近决策边界的样例进行标注，所以策略本身非常适合于SVM这类最小化分类间隔的分类器。SVM由于其内在的高度泛化性能，分类特征可以由一部分支持向量进行表示，所以未标记样本距离分类超平面的距离可以很好地评估一个数据点的信息量。一般情况下，越处于决策边界的点，分类器越难进行处理，人工标记该点所带来的价值远比远离分类间隔面的样本要大，而BvSB方法只考虑样本分类可能性最大的2个类别，如式(3)所示[3]。

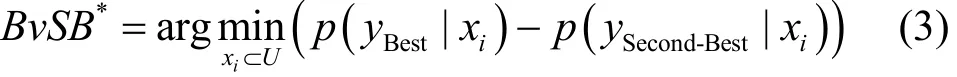
其中，样本xi的最优标号和次优标号的概率分别为p(yBest|xi)和p(ySecond-Best|xi)，通过判断一个样本的最优和次优概率差值的最小值来获取该样本对于决策边界的敏感程度，从而判断出该样本的不确定度。相较于熵值装袋算法而言，BvSB更直观地估计出未标记样本的不确定度，而且对噪声具有天然的处理性能，因为BvSB只关注概率最大的2类，但也正是策略对分类边界的敏感性，所适用的算法多为SVM。

2.2 多策略融合的主动学习算法

集成学习[17,18]的思路是通过训练多个分类器，把所有分类结果进行某种组合（比如投票）决定分类结果，通过使用多个决策者共同决策一个实例的分类从而提高分类器的泛化能力。

对于ESAL算法，也应当满足2点，即策略的差异化和如何对策略进行整合。策略的差异指BvSB和aEQB这2个策略在根本选择样本层面上具有差异。策略结果加权相当于对某个单一策略取出最有价值待标记样本的个数。假设每次迭代待标记的样本个数为N个，而BvSB贡献出的样本个数为B个，aEQB策略贡献出的样本个数为E个，满足式(4)～式(6)。

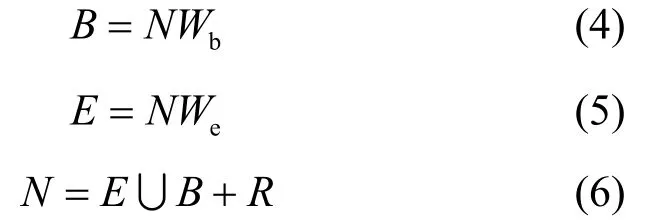
其中，Wb和We为 BvSB和 aEQB的分配权重参数，参数对算法的影响会在实验部分进行讨论。而R是随机跳变因子，若B∩E非空，即在挑选出最有价值的样本相同时，会存在N-的空缺个数，R的作用在于随机挑选符合阈值范围内的价值样本作为补充，值得注意的是，R并非每次存在，而是根据迭代结果来确定，ESAL策略框架如图2所示。

策略融合的本质上只是对挑选策略后的样本进行合并组合，遵循了集成模型的简单易用的特点，对模型的改造而言成本极低，提出的融合方案可横向再次扩充更多的策略进行组合，对于策略的计算方案可采用并行多进程的技术进行实现，理论上实现的时间相较于单模型略有提升。融合策略的主动学习挑选步骤如算法1所示。

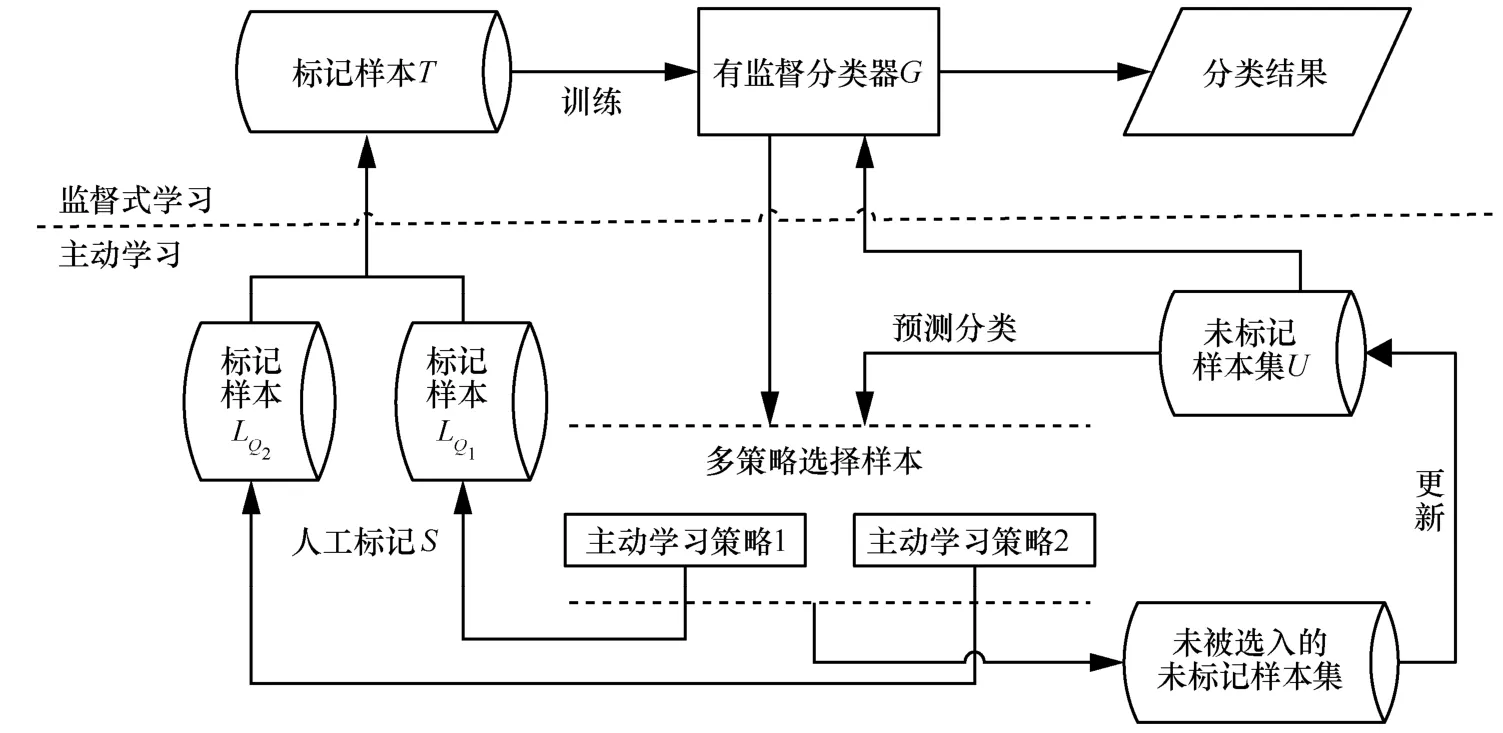
图2 ESAL策略框架

算法1 融合策略的主动学习样本挑选方法

输入 带有极少数随机标记的样本

输出 大量具有标记价值的标记标签

Step1 利用初始样本训练初始模型

Step2 利用未标记的测试样本进行测试，使用式(2)和式(3)进行并行化的策略提取价值样本

Step3 根据式(4)～式(6)进行有价值样本的合并，并进行标记

Step4 利用原始标记样本和Step3中挑选的样本更新原始训练集

Step5 如模型符合条件，则算法结束，否则返回Step1

融合策略的主动学习样本挑选算法伪代码如下。

输入 标记样本T，无标记样本U，期望精度p，每次迭代标记个数N，策略A权重Wa，策略B权重Wb

输出 符合p要求的标签

Repeat：

1) 使用T训练模型Model

2) 使用U当作测试集，进入Model进行分类预测

3) 使用策略 A进行未标记样本的筛选并得出最优价值未标记样本排序LA，使用策略B进行未标记样本的筛选并得出最优价值未标记样本排序LB

4) 在LA有序列表中取出前NWa个，为A策略做出的贡献认为有价值的未标记索引NA，在LB有序列表中取出前NWb个，为B策略做出的贡献认为有价值的未标记索引NB

5) ifNA∩NB非空

R=Number(N-NANB)//即A、B策略产生同样的候选样本，而未达到每次迭代需求，则需要追加跳变因子R

Rindex= Random(LA-NWa,LB-NWb)// 随机挑选A、B策略中排名靠前却未选择的样本

else

R =0

6) 选出的N个候选样本集进行专家标注

7)T = T+N//更新标签集合

8)U = U - N

until 分类精度达到预期p

3 实验数据及指标

3.1 实验数据及设置

AVIRIS数据集是Indian Pines实验区高光谱遥感图像数据。其波长范围为400～2 500 nm，光谱分辨率为10 nm，空间分辨率为17 m，波段数目为220个，共包含16种地物。实验中第104～108、150～163以及第200波段为水吸收波段而被移除，剩下的200个波段，本次用于研究实验数据使用且将数目较多的9种典型地物作为样本。其中，50%的数据集用于训练样本集和候选样本集，实验选择每类5个为初始样本集，剩下的作为未标记集，用于后续迭代添加标签，每次向训练集中添加根据策略选出来的10个样本，算法共迭代100次，总共进行10次，实验取均值。

KSC数据集是美国佛罗里达州KSC实验区高光谱遥感图像数据，光谱波段数量为224个，空间分辨率为18 m，去掉水吸收波段和48个噪声波段，剩下的176个波段作为研究对象。共有13类典型地物样本点5 211个，本次实验选用类别样本数目较多的10种地物，其中，50%的数据集用于训练样本集和候选样本集，这其中选择每类5个为初始样本集，剩下的作为未标记集，用于后续迭代添加标签。算法共迭代100次，每次向训练集中添加根据策略选出来的10个样本，总共进行10次实验。

为了保证实验的可靠性，所采用的是以径向基函数为核函数的 SVM 分类器。aEQB算法中的k值选择为7，即有7个分类器模型构成的委员会[5]。为了充分汲取2种基础算法的优势，实验中使用权重We=Wb=0.5。算法及实验平台选择为Python，算法包来自Scikit-learn，实验机为MacBook Pro 2016 8 GB 2.9 GHz。

3.2 评价参数

除去最基础的总体分类精度（OA）、平均分类精度（AA）和Kappa系数外，新增2个评价指标，从多个角度衡量算法有效性。

3.2.1 人工标记成本

主动学习的原则是尽可能使用较少的标记样本使模型获得相同的训练效果，使用标记样本的个数来表示人工成本，衡量主动学习在迭代阶段所产生的消耗。因为采用批量抽取的技术，所以人工标记成本的最小单位为h，即批处理样本的个数。如果要计算模型达到精度为p时，模型所需要的训练样本个数的人工标记成本计算如式(7)所示。

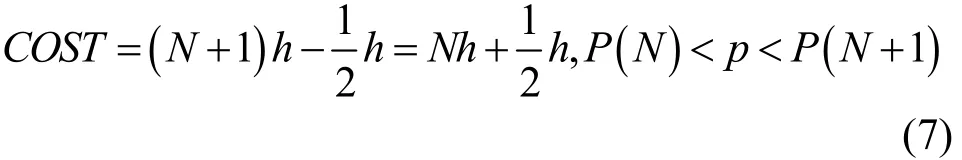
其中，P(N)是第N次迭代时模型的精度。p值可以指定为OA、AA或Kappa系数。举例说明，若要求模型达到OA要求为0.80时，计算主动学习各个样本的成本消耗，那么h=10，p=0.80，假设N=15时符合上述条件，代入式(7)，人工标记成本为

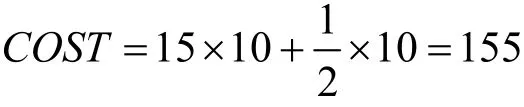
3.2.2 抖动指标

策略结合算法另一个解决的是基策略算法的抖动不稳定现象，所以这里定义抖动指标，2种基础算法发生一次趋势反转，则指标计数加1。

4 实验结果

4.1 Indian Pines和KSC实验结果分析

图3和图4显示了Indian Pines数据和KSC数据实验过程中各类精度曲线爬升情况。从 Indian Pines和KSC的实验结果上来看，3种挑选样本方式的效果要比随机挑选样本效果好，充分证明了样本挑选策略的有效性。横向比较3种挑选样本方式的算法，ESAL算法无论是在OA、AA还是Kappa系数上，都要领先于其他2种基础的算法。

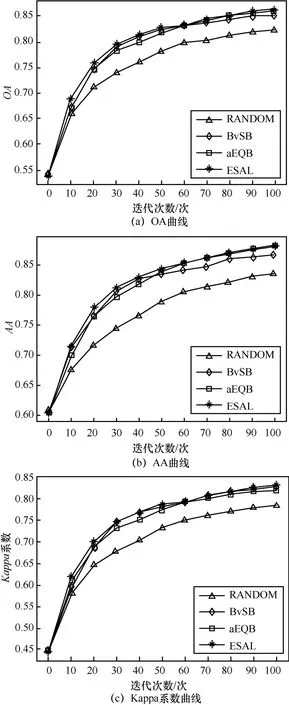
图3 Indian Pines总体分类精度

在Indian Pines数据集中，随机选择RS方法进行的主动学习迭代在最后收敛时总体分类精度只能到达82.33%，而其余的2种主动学习方法在最后都能收敛在85%以上，而提出的融合策略的算法在100次迭代后达到86.35%，处于领先地位。在KSC数据集上，ESAL也有更好的精度表现与更快的收敛速度，在40次迭代时，已收敛到93.4%，在10次迭代时已超过2种基础主动学习方法的0.7%，且一直表现稳定。从平均分类精度上来看，BvSB和aEQB又出现了随迭代次数波动的现象，而融合策略的算法则依旧保持较快的收敛速度和较稳定的增幅，在第7次迭代中，达到最大为 1.1%的增幅，且在后续迭代过程中保持一定领先优势。最终算法收敛于88.95%，高于2种基础的主动学习算法。

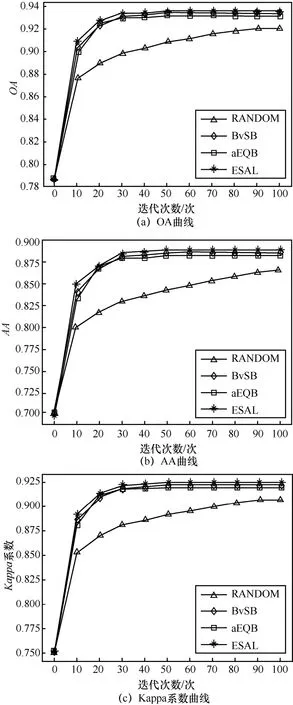
图4 KSC总体分类精度曲线

在算法去抖方面，ESAL始终保持稳定的状态。Indian Pines数据集下，AA的第5次迭代的过程中，ESAL相较于其他2种算法提高了1.7%，之后的迭代的过程中，也始终领先于2种基础算法。并且2种基础策略在迭代过程中出现抖动现象，2种算法的领先开始不断反转，而ESAL始终保持优秀的稳定性。KSC数据集下，从AA爬升阶段看，BvSB和aEQB又出现了随迭代次数波动的现象，而ESAL则依旧保持较快的收敛速度和较稳定的增幅，在第7次迭代中，达到最大为1.1%的增幅，且在后续迭代过程中保持一定领先优势。最终ESAL算法收敛于88.95%，高于2种基础的主动学习算法。

2种数据集的抖动次数如表1所示。从表1可以看出，Indian Pines和KSC数据在实验过程中，单一基础策略并非一直能够保持领先状态，而是出现交替领先的情况，这种情况即为抖动现象，这里，统计的是3种衡量指标下总的波动次数，而使用融合策略的方法，能够极大地减少抖动次数，始终保持更高的精度和更快的收敛速度。

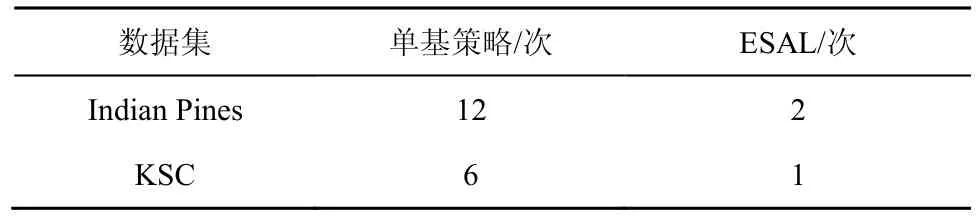
表1 抖动次数

4.2 人工标记成本分析

对于主动学习算法，传统的评价指标并不能很好地表现出算法的优劣，从主动学习根本目标出发，本文提出了标记成本来衡量主动学习算法间的人工损耗。以2组数据在p设定为OA时，各种算法的人工标记成本如图5所示。在使分类器获得相同分类效果时，ESAL算法所需的标记样本始终保持在2种基础算法之下。表2和表3分别显示了各个OA下，不同算法所需要的标记个数。

在Indian Pines数据集中，当OA=0.82时，ESAL相比较于BvSB和aEQB算法而言，标记成本分别减少了50个和80个，相对于2种算法的标记样本数为485个、515个，ESAL将成本率降低了10.3%和15.5%（减少的个数与原先需要的个数的比值），效果明显。而在KSC数据集中，以OA=0.93为例，标记成本相较于2种基础算法依旧减少了50个和80个，但由于KSC本身标记成本较低，故降低的成本率高达17.54%和25.4%，效果突出，并且在标记成本的曲线中，单一策略的波动现象也被很好地表现出来。不同的数据集在不同的爬升阶段，不同的训练样本将会影响策略的效果，如 Indian Pines集数据下，aEQB在迭代后期的表现就比BvSB来得更好，而在KSC数据集下则并非如此，但ESAL始终保持最低的标记成本和最稳定的表现效果。

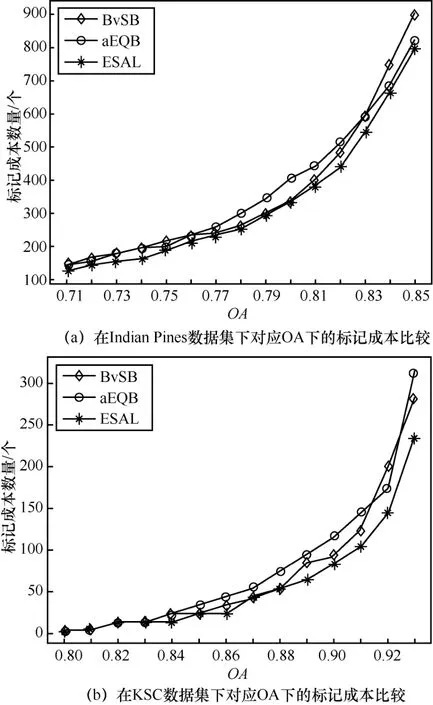
图5 不同算法的对应OA下的标记成本比较

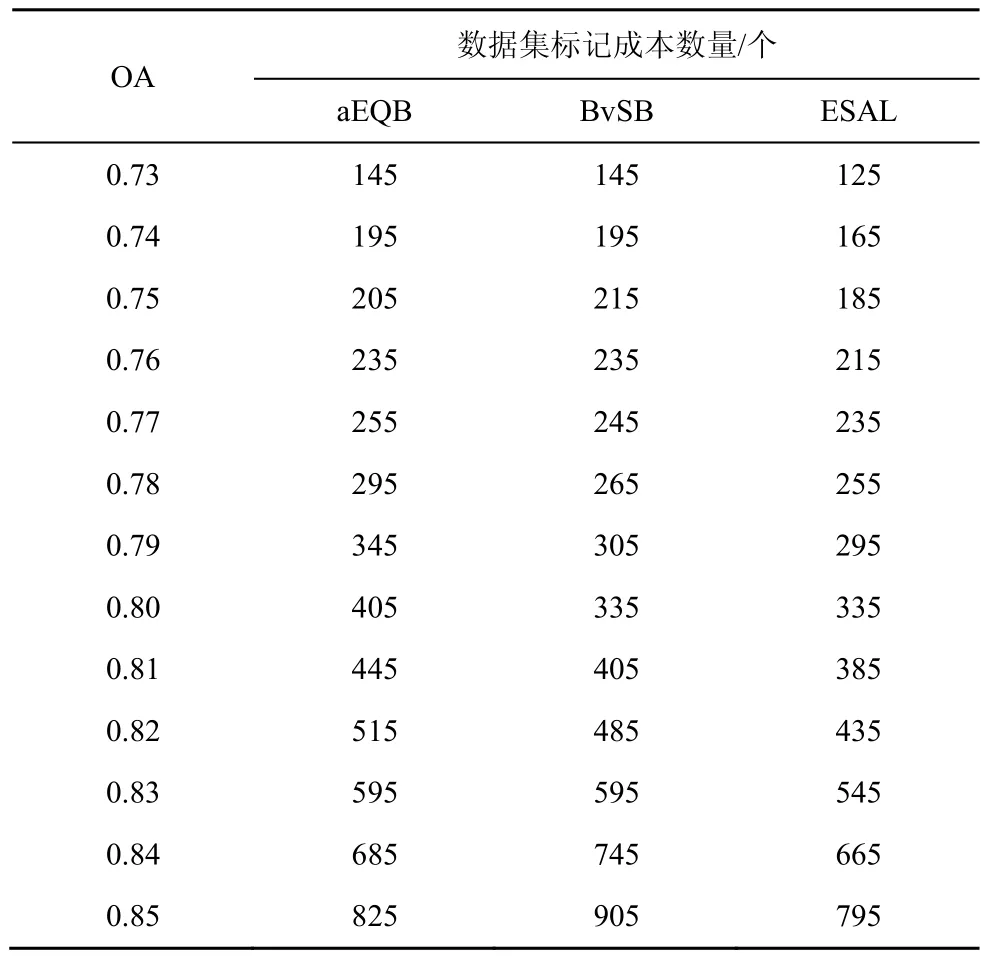
表2 Indian Pines数据集标记成本数量

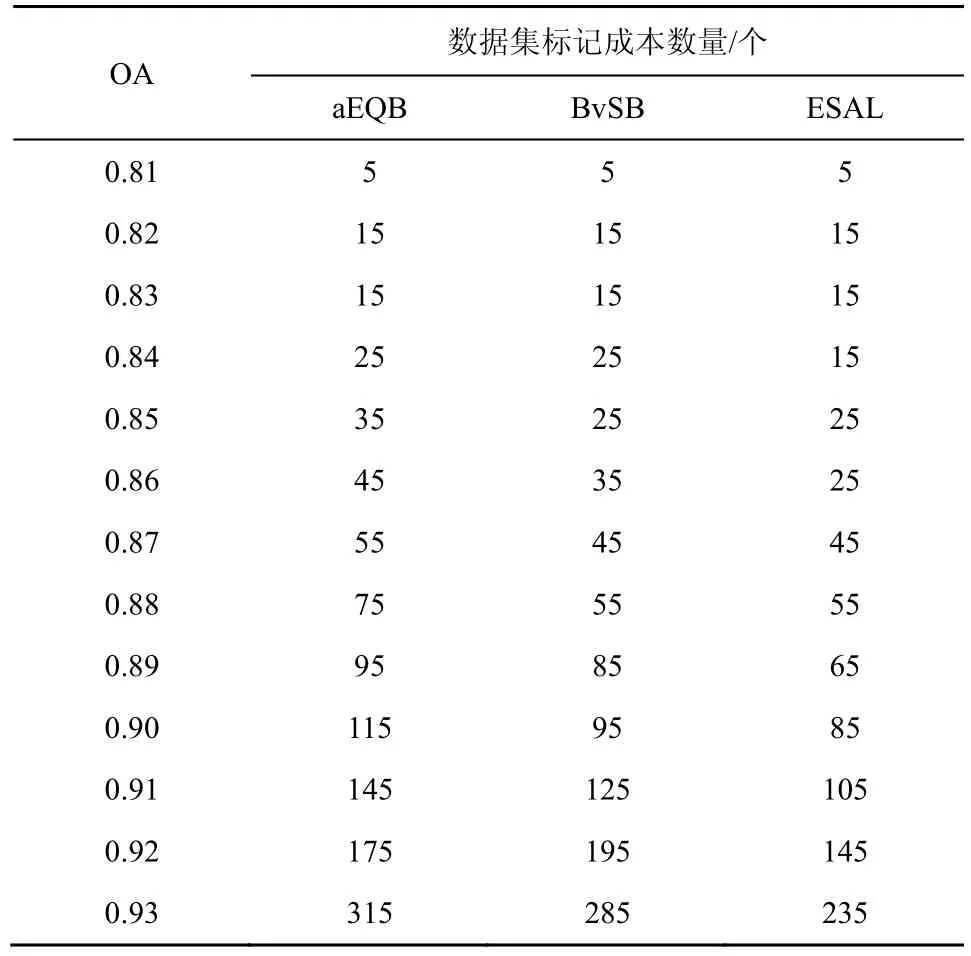
表3 KSC数据集标记成本数量

4.3 权重参数对算法的影响

在使用策略融合时，2种策略的权重配比会对实验效果产生一定的影响。以OA作为阈值指标为例，权重与人工标记成本间的关系如图6所示。

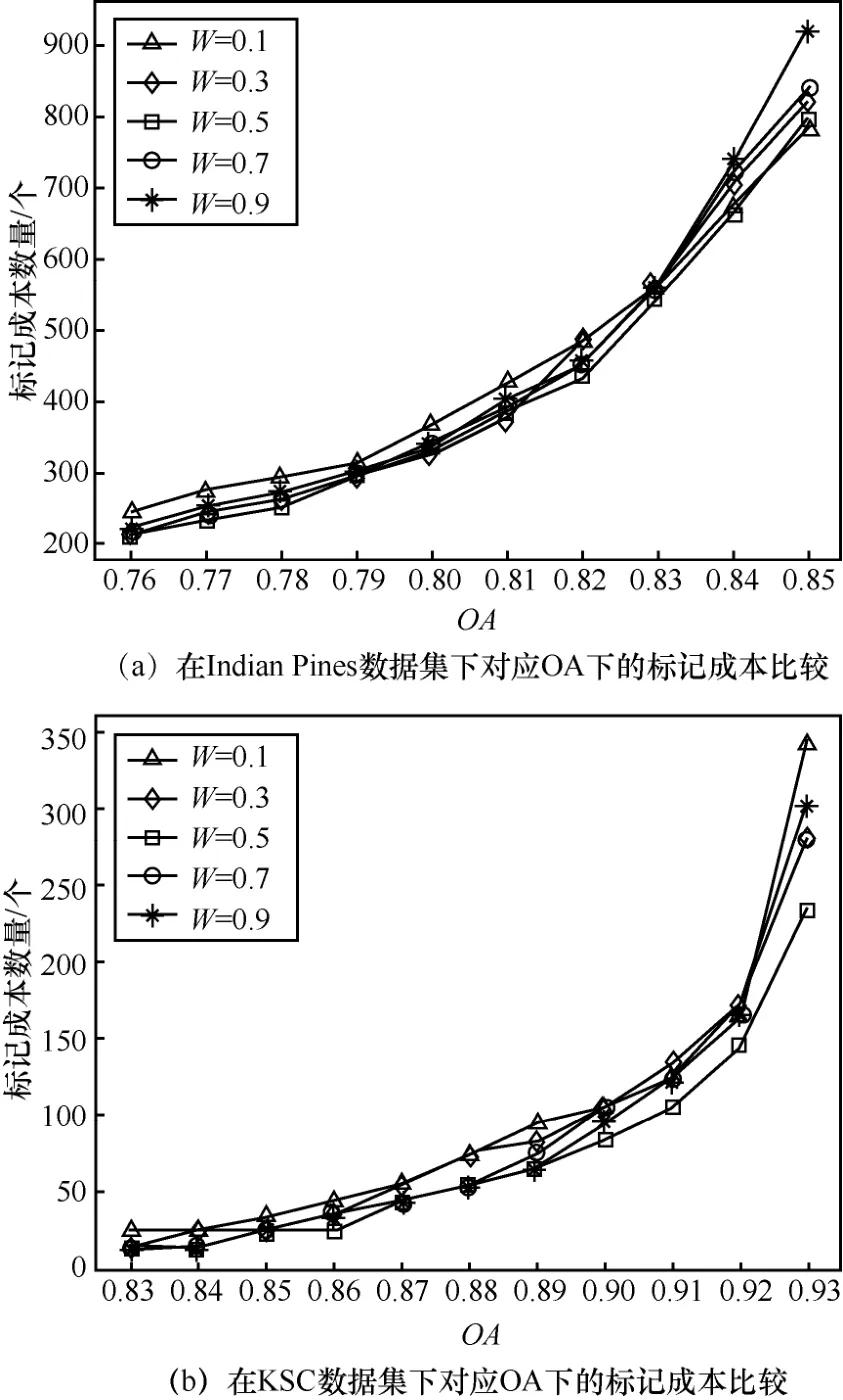
图6 不同算法的对应OA下的标记成本比较

其中，W表示BvSB策略在挑选样本中所占的比例，如本文中，每次挑选的联合样本个数为10，当W=0.1时表示BvSB和aEQB分别挑选1个和9个，以此类推。

从图6中可知，当W=0.5时，在2种数据集中几乎保持最低状态。分析原因可能在于算法需要尽可能地汲取 2个基础策略带来的优势而不是单纯偏向于单一算法。当W=0.1时，表明BvSB只取了1个，实验结果也显示曲线会更加拟合单纯使用BvSB策略的算法，而当W=0.9时，曲线也基本拟合aEQB算法的趋势，表现出实验参数的合理性。

从2个实验数据集中可以看出，配比参数的影响程度表现不一，但都居于W=0.5左右。尤其是在KSC数据上，曲线的抖动较为明显，分析原因可能在于 KSC数据的分类难度较小，较少的样本即能达到收敛效果，但对于更高精度的要求，合理的参数能够更快地突破精度瓶颈。

5 结束语

本文借鉴集成学习的思想对主动学习2种基础策略进行组合改进，提出了一种新的权重组合策略。通过对BvSB和aEQB这2种策略的权重融合，为挑选样本策略引入了差异因素，使整体的组合策略在挑选时集合2种基础策略最优判断的同时，达到2种策略的平衡。通过与标准的基础策略的对比实验发现，所提算法能够极大地降低策略抖动频率，提高策略的稳定程度，在获取相同精度阈值的前提下，降低了人工标记成本。在以后的工作中，可以尝试对其他主动学习基础策略的多次融合。在半监督算法上，可以继续研究利用该融合策略当作新的基础策略参与到半监督算法应用中。

参考文献：

[1]WEI D M M C. Active learning via multi-view and local proximity co-regularization for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Signal Processing,2011,5(3):618-628.

[2]MITRA P,UMA SHANKAR B,PAL S K. Segmentation of multispectral remote sensing images using active support vector machines[J]. Pattern Recognition Letters,2004,25(9): 1067-1074.

[3]JOSHI A J,PORIKLI F,PAPANIKOLOPOULOS N. Multi-class active learning for image classification[C]//2009 IEEE Symposium on The Computer Vision and Pattern Recognition.2009: 2372-2379.

[4]TUIA D,VOLPI M,COPA L,et al. A Survey of active learning algorithms for supervised remote sensing image classification[J]. IEEE Journal of Selected Topics in Signal Processing,2011,5(3): 606-617.

[5]李宠,谷琼,蔡之华. 改进的主动学习算法及在高光谱分类中的应用[J]. 华中科技大学学报,2013,41(11): 274-278.LI C,GU Q,CAI Z H. Improved active learning algorithm and its application in hyperspectral classification[J]. Journal of Huazhong University of Science and Technology,2013,41(11): 274-278.

[6]LI M,WANG R,TANG K. Combining semi-supervised and active learning for hyperspectral image classification[C]// 2013 IEEE Symposium on The Computational Intelligence and Data Mining(CIDM). 2013: 89-94.

[7]WAN L,TANG K,LI M,et al. Collaborative active and semisupervised learning for hyperspectral remote sensing image classification[J]. IEEE Transactions on Geoscience and Remote Sensing,2015,53(5): 2384-2396.

[8]WANG Z,DU B,ZHANG L,et al. A novel semisupervised active-learning algorithm for hyperspectral image classification[J].IEEE Transactions on Geoscience and Remote Sensing,2017,55(6):3071-3083.

[9]王立国,李阳. 融合主动学习的高光谱图像半监督分类[J]. 哈尔滨工程大学学报,2017,38(8): 1322-1327.WANG L G,LI Y. Semi-supervised classification for hyperspectral image collaborating with active learning algorithm[J]. Journal of Harbin Engineering University,2017,38(8):1322-1327.

[10]SAMIAPPAN S,MOORHEAD R J. Semi-supervised co-training and active learning framework for hyperspectral image classification[C]//the Geoscience and Remote Sensing Symposium (IGARSS),2015:401-404.

[11]王立国,杨月霜,刘丹凤. 基于改进三重训练算法的高光谱图像半监督分类[J]. 哈尔滨工程大学学报,2016,37(6): 849-854.WANG L G YANG Y S,LIU D F. Semi-supervised classification for hyperspectral image based on improved tri-training method[J]. Journal of Harbin Engineering University,2016,37(6):849-854.

[12]赵建华,刘宁. 结合主动学习策略的半监督分类算法[J]. 计算机应用研究,2015,32(8): 2295-2298.ZHAO J H,LIU N. Semi-supervised classification algorithm based on active learning strategies[J].Application Research of Computers,2015,32(8):2295-2298.

[13]ZHANG Z,PASOLLI E,CRAWFORD M M,et al. An active learning framework for hyperspectral image classification using hierarchical segmentation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2016,9(2): 640-654.

[14]陈荣,曹永锋,孙洪. 基于主动学习和半监督学习的多类图像分类[J].自动化学报,2011,37(8): 954-962.CHEN R,CAO Y F,SUN H. Multi-class image classification with active learning and semi-supervised learning[J]. Acta Automatica Sinica,2011,37(8): 954-962.

[15]韩松来,张辉,周华平. 基于关联度函数的决策树分类算法[J]. 计算机应用,2005,25(11): 2655-2657.HAN S L,ZHANG H,ZHOU H P. Association function algorithm for decision tree[J]. Journal of Computer Applications,2005,25(11):2655-2657.

[16]QUINLAN J R. Induction of decision trees[J]. Machine Learning,1986,1(1): 81-106.

[17]LIU Y,YAO X. Ensemble learning via negative correlation[J]. Neural Networks,1999,12(10): 1399-1404.

[18]DIETTERICH T G. Ensemble learning[J]. The Handbook of Brain Theory and Neural Networks,2002,2: 110-125.