LT码度分布改进及在认知无线电链路保持中的应用

易本顺，姚渭箐

（1. 武汉大学电子信息学院，湖北 武汉 430072；2. 武汉大学深圳研究院，广东 深圳 518057；3. 国网湖北省电力有限公司信息通信公司，湖北 武汉 430077）

1 引言

认知无线电作为一种有效的技术用于解决频谱资源短缺的问题。次用户可以机会式接入主用户暂未使用的信道[1]，当主用户突然出现时，次用户数据通信被强制中断，需要重构它们的通信链路。这不仅耗时，而且会降低次用户系统的性能。

Willkomm 等[2]首次提出认知无线电系统的次用户链路保持模型，并采用基于冗余纠错码[3]LT码实现对主用户干扰的补偿，随后Yue等[4,5]进行了进一步研究。在该模型的基础上，本文提出一种适用于认知无线电系统的次用户链路保持的新型LT码度分布设计方法。其核心思路是将译码开销较小时具有高译码成功率的度分布与译码开销较大时具有高译码成功率的顽健孤子分布结合在一起来构建新型度分布。首先，对经典的泊松分布（PD,Poisson distribution）函数进行局部改进，并基于 PD的数学特性以及平均度数，推导出λ参数的最优值；然后，基于LT码的期望可译集以及次用户链路的有效吞吐量与 LT码度分布的相关性，构建双层优化目标，采用双层寻优算法（THOA,two-layer hierarchical optimization algorithm）作为寻优工具在IPD与RSD间进行寻优。将改进的LT码作为信道编码应用于认知无线电链路保持中，能最大限度地降低误比特率（BER,bit error rate），同时从一定程度上提高了次用户链路的有效吞吐量。

2 次用户链路保持模型

在基于 LT码的认知无线电次用户链路保持模型[4,5]中，发送端将长度为k×lbit的原始数据均分为k个输入分组；接着，编码器对k个输入分组进行LT编码生成N=k+K个编码分组，其中，K为冗余编码分组的数量；随后，这N个编码分组通过次用户链路的N个并行子信道发送给接收端，即一个子信道传输一个编码分组。接收端接收到任意略大于k且小于N个编码分组，接收端的译码器便能完全恢复k个输入分组，而不需要关心是哪些编码分组用于译码。

如图 1所示，次用户通信的帧结构(tframe)被分为4个部分：感知时间段(tsens)、控制时间段(tcontrol)、获取时间段(tacquire)和数据传输时间段(tdata)。其中，tsens、tcontrol和tacquire一起构成链路保持时间。在tsens中，通过频谱感知确定未被主用户使用的子信道。在tcontrol中，发送端和接收端之间互换感知结果，并达成共识，决定哪些子信道必须排除，而哪些子信道则可以用来通信。tacquire为获取新子信道所需的时间。tdata为信息在当前次用户链路上的传输时长。

假设所有子信道干扰概率都是相等的，并且不同子信道的干扰概率是独立的。同样，对于连续的时间帧，子信道干扰概率也是独立的。

定义ne表示解调和译码后丢失的数据分组，Pne表示丢失ne个数据分组的概率，E表示译码失败事件。由于当ne＞K时，信息错误概率为1，于是得到LT码的总信息错误概率[4]为

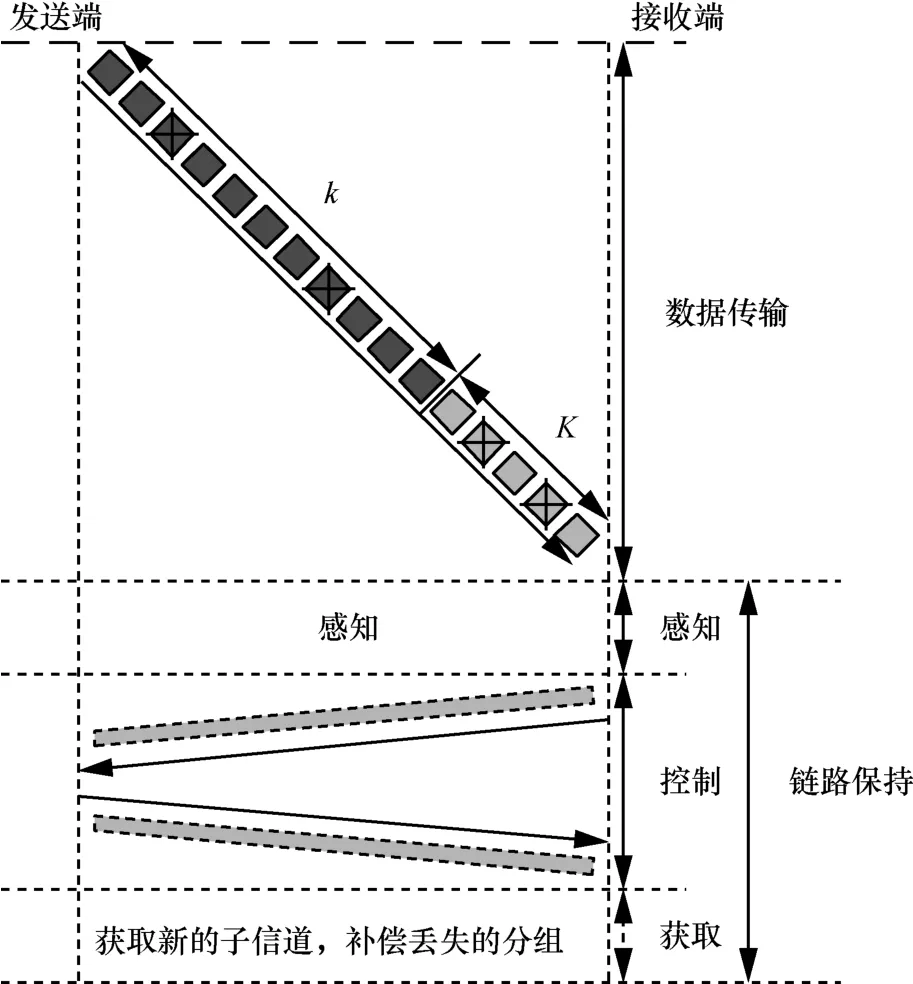
图1 次用户通信的帧结构

定义pI为子信道总干扰概率，表示为

其中，pPU为主用户的干扰概率，pa为信道质量较差时译码失败概率。

Pne表示为

定义Ndec为k×lbit的数据信息完全成功译出所需的比特数量，于是得到

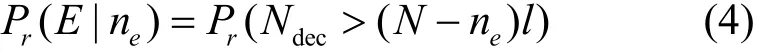
定义Pa为次用户链路保持的概率，即在上一个帧内，正在被次用户链路使用的子信道中，至少一个被主用户占用从而需要重新获取子信道的概率。根据式(3)，Pa可表示为

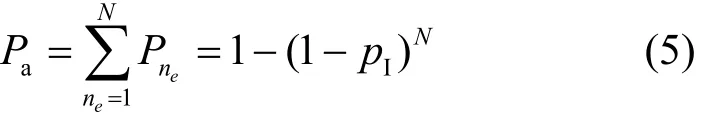
根据式(5)，时间帧的平均长度可表示为

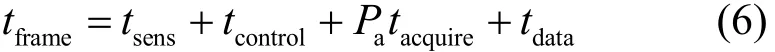
从而得到平均有效吞吐量为

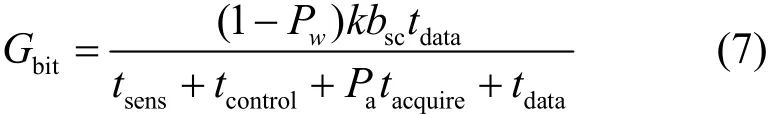
其中，bsc为子信道的比特率。

3 LT码原理

3.1 LT码编译码过程

LT码的编码过程非常简单，具体步骤如下。

Step1 从度分布中随机选择一个度d。

Step2 随机且均匀地选取d个原始分组。

Step3 将这d个输入分组进行异或（XOR）生成一个编码分组。

通常，LT码采用BP算法进行译码，具体步骤如下。

Step1 度数为1（d= 1）的编码分组直接译码。

Step2 译出的原始分组与跟其相连的编码分组进行异或后替代原编码分组，同时删除其连接关系。

Step3 重复步骤Step1和Step2，直至译码完成。LT码编译码过程如图2所示。

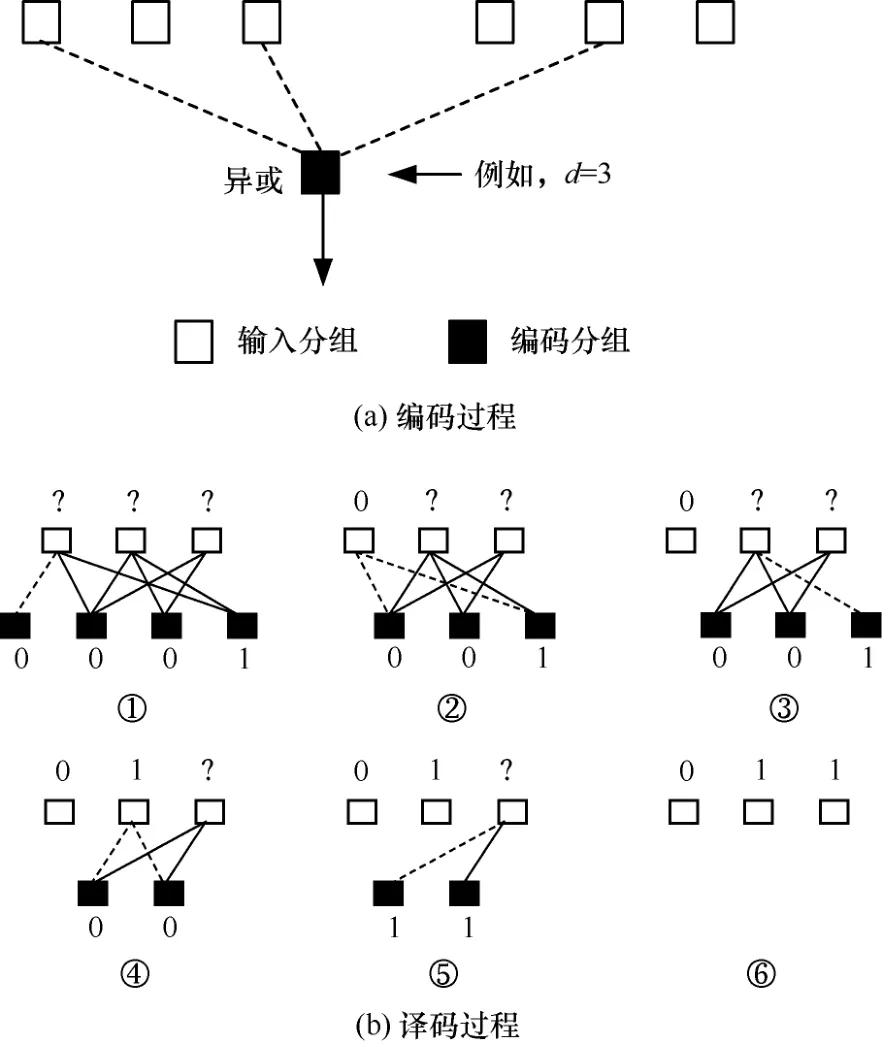
图2 LT码编译码过程

3.2 LT码经典度分布

其中，Ωd是一个编码分组选取度数为d的概率，并

LT过程的随机行为完全取决于度分布Ωd，编码分组数量N以及输入分组数量k。一个好的度分布需满足2个设计目标。

1) LT过程成功所需的平均编码分组数量尽可能少，确保 LT过程成功的编码数量对应于确保原始数据全部恢复的编码分组数量。

2) 编码分组的平均度数尽可能小，平均度数是生成一个编码分组所需的平均 XOR运算次数。平均度数乘以N就是恢复原始数据所需异或运算的平均次数。

常见的 LT码度分布有理想孤子分布（ISD,ideal soliton distribution）和 RSD[3]。

1) 理想孤子度分布

ISD表示的是一种理想情况，即在每次译码迭代中，只有一个度为1的编码分组，并且在每次迭代译码之后，只出现一个新的度为1的编码分组。其度分布函数为

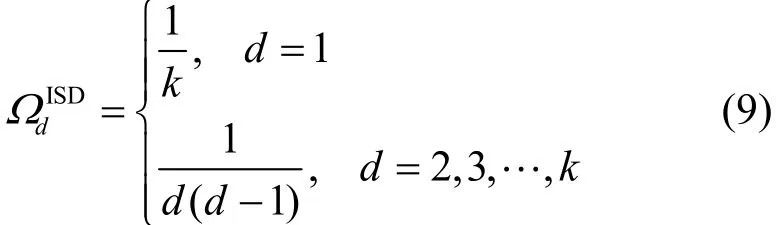
其中，d为每个编码分组的度，k为原始分组数量。

然而，这种度分布的实际性能很差，一个很小的偏差就会导致度为1的编码分组消失从而造成译码终止。

2) 顽健孤子度分布

针对ISD的不足，RSD在度分布函数中引入2个参数c和δ，期望度为1的编码分组数量在译码过程中始终保持为其中，k为原始分组数量，c为大于0的常数，δ为译码失败概率。

首先，定义一个函数

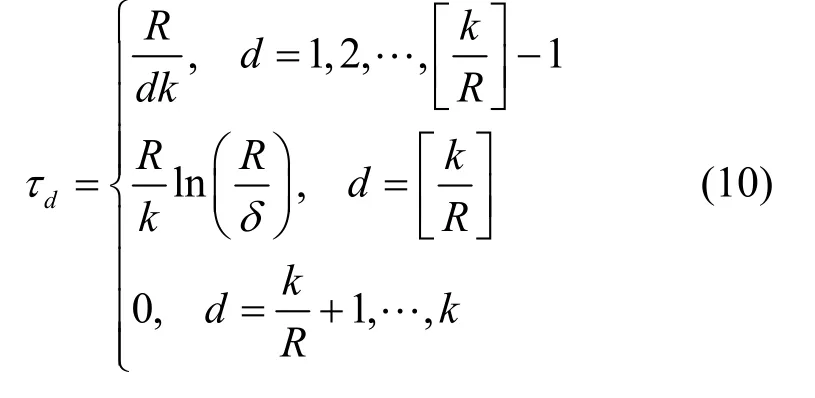
尽管RSD优于ISD，但采用RSD进行LT编码所产生的编码分组多为度数较大的编码分组，在译码过程中可能会由于缺少足量度数较小的编码分组而导致译码中断。

4 LT码度分布改进方法

4.1 改进的泊松分布

大量的研究工作证实，一个好的度分布具有某些特征[6]。度分布中某些度数的比例对LT码的可译码性起主导作用。一个重要特征是度数为2在度分布中所占比例最高。在 BEC中，为保证译码率，需要同时，度数为1的编码分组的比例必须要小[8～10]。因此，LT码可通过调整这些度数的比例获得良好的性能。

基于度分布特性，通过调整度数为2的比例对PD进行改进来获得更高的初始译码成功率。改进的泊松分布（IPD,improved Poisson distribution）为

然后，对函数μd进行归一化，得到IPD函数ΩdIPD为

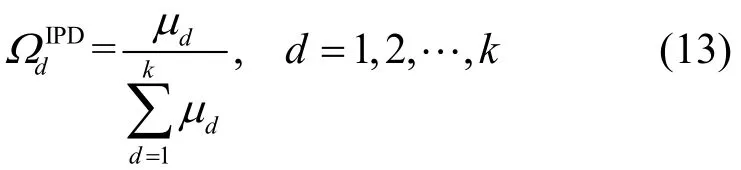
其中，λ是为大于0的常数。

参数λ直接影响LT码的编译码过程，因此，有必要为其选择合适的参数值。为了满足一个好的度分布的设计需要[3]，编码分组的平均度数越小越好。IPD和ISD平均度数的问题可转换为和(式(9))均值的问题。和均值的表达式为

ISD表示的是一种理想情况，即编码分组进入可译集的速度与移除的速度相同[3]。理想情况下，λ的参数值可通过和值相等来推出。均值将会随k增加而增大。基于PD的数学特性，当k< 2 0时PD近似于BD[11]。因此，考虑从k=20点推导出λ的参数值。根据当k= 2 0时

假设输入分组k= 1 000，RSD、PD和IPD度分布函数的概率分布如图3所示。得到λ≈3.04。

图3 RSD、PD和IPD概率分布

为了验证IPD性能，采用IPD对LT码进行1 000次编译码仿真。当λ选取不同参数时，IPD成功译出的输入分组比率随译码开销变化情况的仿真结果如图4所示，表示译码开销，N为译码成功所需编码分组个数。很明显，当λ=3时，IPD具有较好的译码性能，随着译码开销的增加，译码成功率一直保持较高的状态，甚至可达 90%以上。不足的是，当译码开销较大时，RSD（参数c=0.1,δ=0.005）的译码性能表现更佳，而此时IPD的译码成功率上升速度减缓。因此，验证了IPD在译码开销较小时具有高译码成功率的度分布，而 RSD在译码开销较大时具有高译码成功率的度分布。

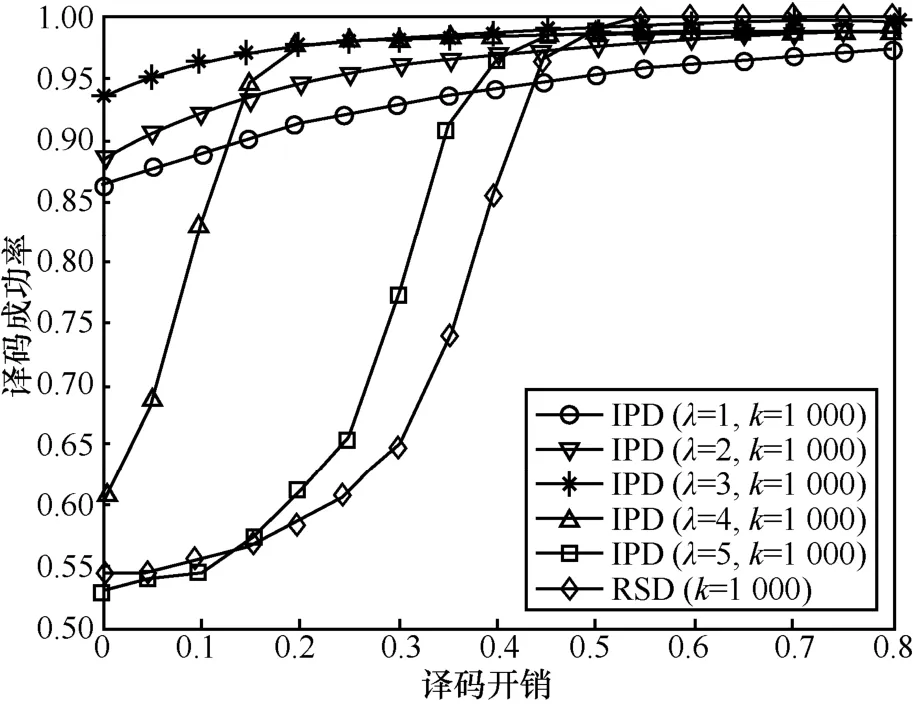
图4 IPD和RSD的译码成功率

4.2 基于两层递阶优化算法的度分布优化

为了将IPD和RSD的优点进行有机结合，考虑采用优化算法在2种度分布间进行寻优得到BER性能更佳的度分布，从而提高认知无线电次用户链路的通信可靠性。同时，优化过程中还需要考虑次用户链路的通信可靠性。

改进的度分布优化方法基本思路如下。首先，分析LT码的可译集和次用户链路的有效吞吐量这2个因素与度分布的关联性来构建目标函数；然后，通过最大化目标值，采用两层递阶优化算法（THOA,two-layer hierarchical optimization algorithm）对度分布进行寻优；此外，为提高THOA的全局搜索能力，提出一个搜索算法来动态调整搜索域。

4.2.1 2个重要因素与度分布关联性研究

1) 可译集

LT码的BER性能是衡量认知无线电次用户链路保持系统的通信可靠性的重要标准。本文通过优化度分布来改善BER性能，而LT码可译集一定程度上反映度分布与LT码译码性能的相关性。

可译集是LT译码过程中度为1的编码分组集合，一定程度上反映译码成功率和度分布函数之间的关系。在译码过程的每一步中，一方面，随着译出的原始分组与跟其相连的所有编码分组之间的连接关系在 XOR运算后被移除，度数较高的编码分组便变成度数为1的编码分组，从而进入可译集；另一方面，度数为1的编码分组直接被译出后便从可译集中移出。因此，可译集的大小在译码过程中不断发生变化。对于一个好的度分布来说，希望产生足够多的度数为1的编码分组的同时，能尽可能降低这种波动幅度。Karp等[12]第一次提出期望可译集的表达式。

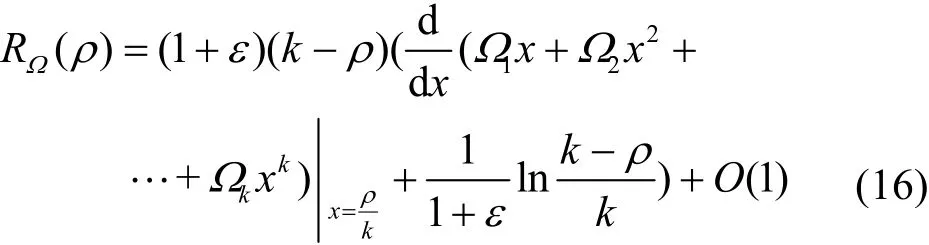
其中，Ω(⋅)为度分布，k为原始分组数量，ρ表示成功译码的原始分组数量。表示LT码译码开销，即次用户链路保持模型中子信道的冗余开销。

基于上述理论分析，本文通过增大期望可译集均值并同时降低其方差[13]，即最大化式(17)来获得优化度分布。

其中， α ∈ (0,1)。α过大会降低均值的容忍度。如果α=0，目标则转化为求期望可译集方差的最大值。通常情况下，将α的取值范围设置为0到1之间，本文设置 α = 0 .25。

2) 有效吞吐量

另外一个重要因素是次用户链路的平均有效吞吐量，用作衡量认知无线电次用户链路保持系统的通信有效性。期望通过优化度分布来提高次用户链路的有效吞吐量并降低达到最大有效吞吐量所需的冗余子信道数量，所以需要找到有效吞吐量与度分布关联性。

根据LT码编译码原理可知，生成N个编码分组总共需要进行 N E[Ωd]次异或运算，即编码分组与输入分组之间总共存在 N E[Ωd]个连接关系。在一个随机编码过程中，每个输入分组未参与编码的概率为因此，可计算出输入分组的漏选概率为在所有参与编码的输入分组全部被译出的理想情况下，输入分组的漏选概率即无法避免的译码失败概率，因此，输入分组的漏选概率直接影响LT码译码性能。将 Pr(E| ne)近似为无法避免的译码失败概率，表达如下。

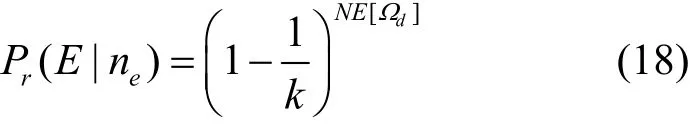
将式(18)代入式(1)得

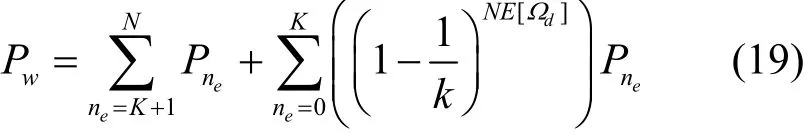
基于以上分析，与度分布相关的有效吞吐量可表示为

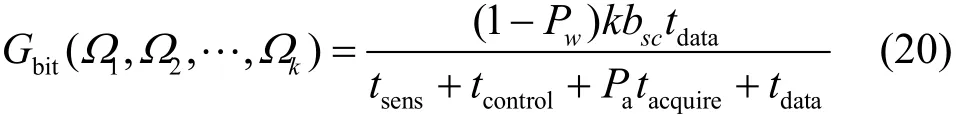
其中，

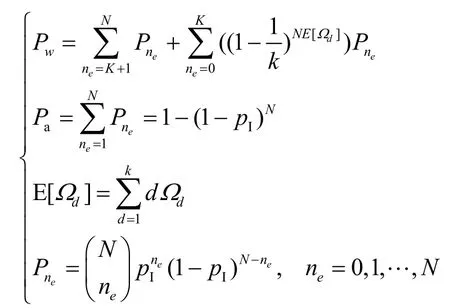
4.2.2 算法设计

为防止寻优过程中搜索结果超出边界而为负值，设计一种动态搜索算法（DSA,dynamic search algorithm），对寻优算法的每一步骤中的搜索域和步长进行动态调整，从而提高搜索能力和收敛性能。

DSA算法具体实现步骤如下。

Step1 基于IPD和RSD产生初始度分布，例如，集合大小为m，有k个待优化的参数，即要随机产生一个k行m列初始度分布集合{Ωj|j=1 ,2,…,m}。每个度分布表示为向量Ω= (Ω1,Ω2,… ,Ωk)，其中d= 1 ,2,3,… ,k。在第一次迭代中，

Step2 每个度分布Ω在Region内进行随机搜索nb个度分布{φi|i= 1 ,2,…,nb}。其中，每个度分布为φ= (φ1,φ2,… ,φk)，每个度数φd,d= 1 ,2,3,…,k的选取过程可以表示为

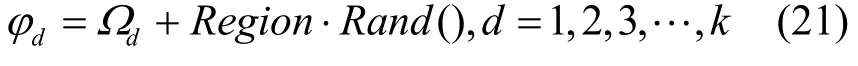
Step3 比较这nb个度分布的目标函数值，选取函数值最大/小者作为该集合{φi|i= 1 ,2,…,nb}的最优值φlocal。

Step4 比较φlocal和Ω的目标函数值，如果φlocal的目标函数值大于Ω的目标函数值，表明φlocal优于Ω，则Ω朝φlocal方向前进一步，否则保持不变，该过程可以表示为

其中，Step=0.5Region。

Step5 动态调整Region，该过程可以表示如下。

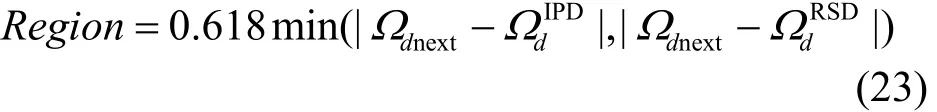
本节验证新型LT码度分布优化方法（简称为THOA度分布）对于认知无线电次用户链路保持的有效性。将分别从LT码的误比特率（BER）性能和次用户链路的有效吞吐量2个方面进行评估。假设该认知无线电系统模型有N= 1 00个信道，并且添加K个子信道用于保持次用户链路的通信质量。将一个长为10 000 bit的原始数据信息均分为100个输入分组。

选取参数c=0.1和δ=0.5，分别采用RSD和

Step6 如果迭代次数小于设定值，转移到步骤Step2；否则，度分布Ω搜索到其局部最优度分布Ωglobal。从而得到m个度分布各自的局部最优度分布 {Ωjglobal|j=1 ,2,…,m}。

Step7比较 {Ωjglobal|j=1 ,2,…,m}的目标函数值，得到全局最优度分布Ωbest。

设计THOA算法对度分布进行寻优，将LT码的纯理论研究过渡到认知无线电系统的实际应用中。主要思路是将搜索过程分为2层结构。首先在IPD和RSD的动态搜索域中选择合适的初始度分布集；接着进行第一层寻优，基于可译集特性搜索最优度分布；将第一层的优化结果用作第二层的输入集；随后进行第二层寻优，基于有效吞吐量特性获得最优度分布。THOA算法的过程如下。

Step1 构建M个初始度分布集合其中，通过

1,2,3,…,k选取初始集合。

Step3 采用 DSA算法作为寻优工具，以最大化式(17)为目标，搜索得到最优度分布Ωbest。从而得到这m个分组的最优度分布集合

Step4m个组的寻优结果用作第2层的输入集。

5 实验仿真

THOA对100个输入分组进行编码。基于1 000次编译码仿真结果，分析和比较这2种方法的BER。当 K = 3 0、40、50、60时，不同干扰概率下 RSD和THOA的BER比较如图5所示。

可明显看出，当冗余子信道的数量相同时，随着干扰概率减小，2种方法的BER都逐渐降低。相比RSD、THOA的BER性能始终表现较优。如图5(c)所示，假设链路存在 50个冗余子信道，当pI=0 .01时，THOA的BER仅为 3 .68×1 0-3，明显低于RSD；而当 pI= 0 .001时，THOA的BER降低到1.87×1 0-3，BER性能依旧优于RSD。并且，随着冗余子信道的数量增多，即接收端接收较多编码分组，2种方法的 BER都有明显降低，THOA的BER性能始终占有绝对优势。例如，在相同干扰概率 pI=0 .001下，当 K = 3 0时，THOA的 BER为2.49×1 0-2，RSD的BER为 3 .26×1 0-1；当 K = 6 0时，THOA的BER降低到 5 .10×1 0-4，RSD的BER为3.11×1 0-3。

图5 THOA和RSD误比特率

另一个重要的性能指标是次用户链路的有效吞吐量。文献[2]证实信息错误概率与链路保持概率之间存在一个折中。使用更多数量的冗余并不一定能带来更大的有效吞吐量。更多数量的冗余提高了链路保持概率，但是却降低了次用户链路的有效吞吐量。因此，为了获得可能的最大有效吞吐量，有必要选择最优的冗余子信道数量。本文假设每个子信道的

有效吞吐量随冗余子信道数量的变化情况如图6所示。可以看到，随着子信道数量增加，RSD和THOA这2种方法的次用户链路的有效吞吐量都逐渐增大。当达到最大有效吞吐量以后，再随着子信道数量增加，有效吞吐量则开始非常缓慢地下降，但几乎看不出。

随着干扰概率的增大，达到最大有效吞吐量所需的冗余子信道数量也增多。如图 6(b)所示，当pI= 0 .01时，采用RSD方法进行LT码编码，需要80个冗余子信道，次用户链路才能达到最大有效吞吐量，而THOA方法则只需35个。当 pI= 0 .05时，采用RSD方法进行LT码编码，需要90个冗余子信道，次用户链路才能达到最大有效吞吐量，而THOA方法则只需45个冗余子信道，降低了频谱资源消耗。可以明显看出，相比RSD、THOA方法达到最大有效吞吐量所需的冗余子信道数量最少。

6 结束语

本文研究了一种适用于认知无线电链路保持的新型LT码度分布设计方法，将译码开销较小时拥有高译码成功率的IPD与译码开销较大时拥有高译码成功率的RSD进行有机结合。基于LT码的期望可译集以及次用户链路的有效吞吐量与LT码度分布的相关性，构建双层优化目标，采用双层寻优算法作为寻优工具在2种度分布间进行寻优，实现了次用户通信可靠性和有效性的提高。

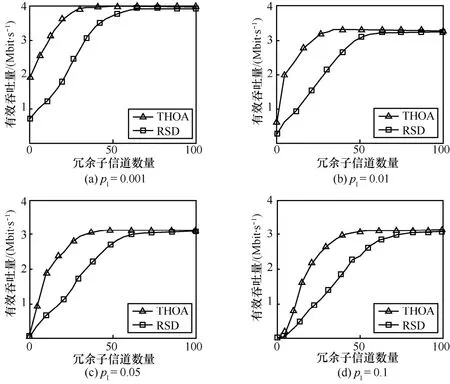
图6 THOA和RSD有效吞吐量

参考文献：

[1]张勇,滕颖蕾,宋梅. 认知无线电与认知网络[M]. 北京：北京邮电大学出版社,2012.ZHANG Y,TENG Y L,SONG M. Cognitive radio and cognitive networks[M]. Beijing: Beijing University of Posts and Telecommunications Press,2012.

[2]WILLKOMM D,GROSS J,WOLISZ A. Reliable link maintenance in cognitive radio systems[C]//2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. 2005: 371-378.

[3]LUBY M. LT codes[C]//43rd Annual IEEE Symposium on Foundations of Computer Science. 2002: 271-280

[4]YUE G,WANG X. Anti-jamming coding techniques with application to cognitive radio[J]. IEEE Transactions on Wireless Communications,2009,8(12):5996-6007.

[5]YUE G. Antijamming coding techniques[J]. IEEE Signal Processing Magazine,2008,25(6):35-45.

[6]LIAU A,YOUSEFI S,KIM I M. Binary soliton-like rateless coding for the Y-network[J]. IEEE Transactions on Communications,2011,59(12): 3217-3222.

[7]ETESAMI O,SHOKROLLAHI A. Raptor codes on binary memoryless symmetric channels[J]. IEEE Transactions on Information Theory,2006,52(5): 2033-2051.

[8]MACKAY D J C. Fountain codes[J]. IEEE Proceedings Communications,2005,152(6): 1062-1068.

[9]HYYTIÄ E,TIRRONEN T,VIRTAMO J. Optimizing the degree distribution of LT codes with an importance sampling approach[C]//6th International Workshop on Rare Event Simulation. 2006.

[10]SHOKROLLAHI A. Raptor codes[J]. IEEE Transactions on Information Theory,2006,52(6): 2551-2567.

[11]盛骤,谢式千,潘承毅. 概率论与数理统计(第四版)[M]. 北京: 高等教育出版社,2010.SHENG Z,XIE S Q,PAN C Y. Probability theory and mathematical statistics (4th ed) [M]. Beijing: Higher Education Press,2010.

[12]KARP R,LUBY M,SHOKROLLAHI A. Finite length analysis of LT codes[C]//International Symposium on Information Theory. 2004.

[13]YEN K K,LIAO Y C,CHEN C L,et al. Modified robust soliton distribution (MRSD) with improved ripple size for LT codes[J]. IEEE Communications Letters,2013,17(5): 976-979.

[14]焦健,杨志华,顾术实,等.基于随机置换展开与停止集的 LT 码联合编译码算法[J].通信学报,2013,34(2): 31-39.JIAO J,YANG Z H,GU S S,et al. Novel joint encoding/decoding algorithms of LT codes based on random permute egde-growth and stopping set[J]. Journal on Communications,2013,34(2): 31-39.