基于遗传算法优化参数SVM的备件需求预测研究
邱立军,付霖宇,董 琪,顾钧元
(海军航空工程学院 a.科研部; b.兵器科学与技术系, 山东 烟台 264001)
备件保障是装备维修保障非常重要的组成部分,随着对装备实战化要求的不断提高,越来越受到重视[1]。作为装备保障的关键部件,其特征是价格昂贵、使用量少、间隔期长、对可靠性要求高,历史需求数据的样本量有限。在需求预测的方法中,大多数预测方法要求预测数据充分大,只有这样预测精度才能保证。目前,指数平滑法在装备保障需求分析中得到广泛应用,因其对样本的规模要求比较小,按照处理程度扩展出一次法(简单指数平滑法)、二次法和三次法[2-5]。但指数平滑法受数据量大小的影响较为敏感,当备件样本量减少到一定程度,预测结果偏差较大。
支持向量机理论引入装备保障领域,主要解决了针对小样本和非线性问题,特别是分类和预测方面。文献[6]利用有向无环图支持向量机方法对装备不常用备件进行分类,取得了良好的效果。文献[7]通过支持向量机回归算法构建了备件需求模型,并利用十折交叉验证法进行精度测试。文献[8]研究了支持向量机回归算法,并与Croston方法、Bootstrap方法进行对比;文献[9]将最小二乘法与支持向量机相结合,均通过实例验证了方法的优势,但未对算法中的参数优化问题进行深入研究。
综上所述,为提高小样本备件预测精度,本文利用支持向量机回归原理,提出了基于支持向量机的备件预测方法,对其中的参数优化问题进行了重点研究,提出了利用遗传算法优化参数的方法,通过规划计算流程和编写相应程序,通过实例对某装备备件的需求量进行了预测,并分别与指数平滑法、网格搜索法优化参数的支持向量机方法进行对比分析。
1 指数平滑法
指数平滑法通过引入平滑系数,将输入数据对输出结果的影响在时间上映射为由近到远呈非线性递减的关系,利用“误差反馈”原理逐次对预测量进行“平滑”,达到减小预测误差的目的[10]。
预测模型为
(1)

由式(1)可知,指数平滑法计算的重点在于确定合理的α值。确定的原则可参考文献[11]。在工程实际应用中,宜选取多个α进行试算,通过误差对比确定最佳α值[11]。
2 备件需求预测模型构建
支持向量机理论在统计学的回归算法的研究中,体现出较好的拟合小样本的优点[12]。与神经网络等仿真方法相比,该方法通过求解转化的凸二次规划问题,得到全局最优解,有效地降低了计算维数,提高了运算效率[13-14]。备件需求预测问题在一定程度上可抽象为数据统计问题,因此,将该方法引入备件保障领域具有良好的应用前景。
以备件的历史需求数据作为输入,利用支持向量机理论,构建备件需求预测模型,步骤如下(流程见图1):
步骤1:提取备件需求x的历史数据{xi,x2,…,xn},xi表示第i期的备件需求,i=1,2,…,n;
步骤2:运用极差变换法将每期的备件需求量均变为属于[0,1]区间的值;
步骤3:利用RBF核函数对参数进行优化,获得最优参数;
步骤4:求解回归问题,得到SVM预测函数;
步骤5:根据SVM函数预测备件需求,并进行精度分析,若达不到精度要求,重新调整核函数,转步骤4;若达到精度要求,生成合适的SVM预测函数;
步骤6:将结果增加到备件需求的历史数据中,保存模型。
支持向量机核函数和预测函数的具体处理遵循常规处理方法,其中核函数选择RBF核函数,预测函数选择通过约束目标函数进行寻优,具体可参见参考文献[6-9]。
根据上述建模流程,通过Matlab2008a软件来设计并实现仿真程序,其中的支持向量机组件是由台湾大学林智仁教授编写的libsvm工具箱[15]。
为了适应支持向量机的对数据的要求,减少误差,更加准确的进行需求预测,采用极差变换法对输入数据进行归一化处理[16]:
步骤1:确定输入数据的两个最值,即MAX,MIN;
步骤2:利用式(3)得到第t年的需求量Xt。
(3)
3 需求量预测准确度评价
准确度评价可采用平均绝对误差(MAE,Mean Absolute Eror)、均方误差(MSE,Mean Squared Error)以及正则化均方误差(NMSE,Normalized Mean Squared Error)。
由于MSE计算较为简便,应用范围最广。因此,本文采用MSE作为需求预测的评价指标。公式如下:
(4)
4 实例分析
本节对某型装备备件消耗数据进行分析(如表1所示),由于该型装备数量少,历史消耗数据样本较小。
通过极差变换法[17],将表1数据转化为[0,1]区间的值,归一化处理后的数据如表2所示。
由表2数据拟合得到数据需求图,如图2所示。
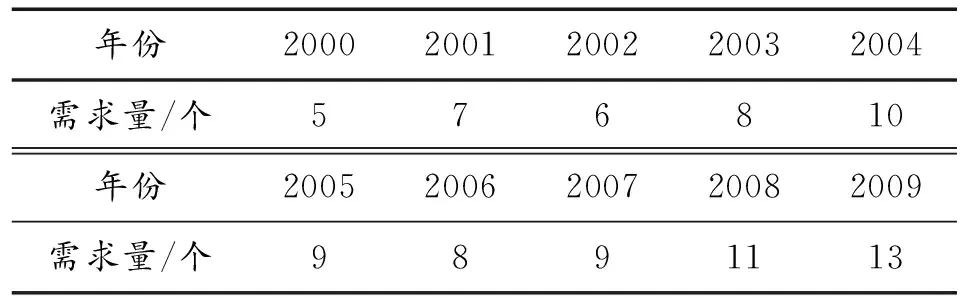
表1 备件历史需求数据
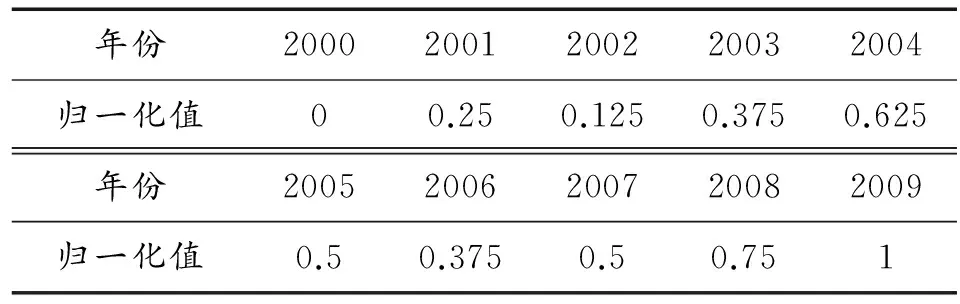
表2 归一化数据
由图2可知,通过极差变换归一化处理后的数据,并不改变各期需求量之间的相对关系。因此,不会影响到需求预测模型的构建。
若采用传统的指数平滑法,由于输入数据的波动幅度较大,α取0.8(α=0.8),并以2000年和2001年数据的平均值作为初始值。
由图3可知,预测曲线与实际数据的拟合性能不是很好,经计算得到MSE=26.54,2009年备件的实际需求量是13个,经指数平滑法预测得到的结果是10.45,取整后为11个,相差2个。
运用本文模型进行需求量预测[18-19]。选择RBF核函数,将惩罚系数C和核参数g作为寻优变量,使其值在一定范围划分网格并遍历网格内所有点进行取值,以均方误差(MSE)最小为优化目标,利用网格搜索法,采用libsvm工具箱对函数进行优化,选择C=1 024,g=0.031 5。得到参数寻优图及备件需求量预测,如图4和图5所示。
由图5可知,预测曲线与实际数据的拟合性能较好,经计算得到MSE=7.191,2009年备件的实际需求量是13个,经网格搜索法优化参数的支持向量机预测得到的结果是12.31,取整为13个。
若将参数优化的方法改为遗传算法,并选择C=121.034 5,g=0.498 3。适应度函数及备件需求量预测曲线如图6和图7所示。
由图7可知,预测曲线与实际数据的拟合性能很好,经计算得到MSE=5.398,2009年备件的实际需求量是13个,经遗传算法优化参数的支持向量机预测得到的结果是12.43,取整为13个。
最后,将3种方法进行对比分析,得到表3。
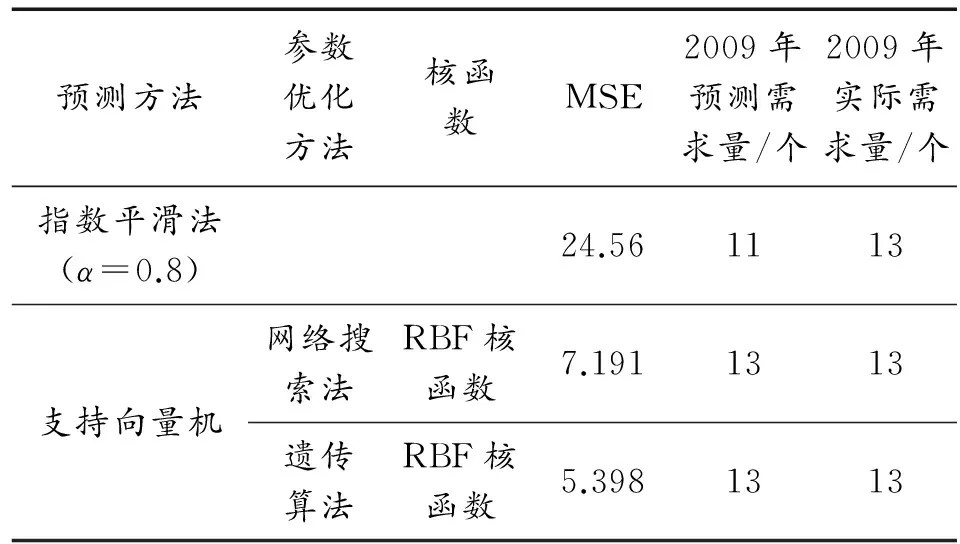
预测方法参数优化方法核函数MSE2009年预测需求量/个2009年实际需求量/个指数平滑法(α=0.8)24.561113支持向量机网络搜索法RBF核函数7.1911313遗传算法RBF核函数5.3981313
由表3可知,指数平滑法得到的MSE为24.56,远大于支持向量机方法结果,说明精度最差。支持向量机的预测效果很好,尽管预测量同为13个,但遗传算法得到的具体计算值更接近实际值。因此,当采用网格搜索法优化参数时,MSE为7.191,当采用遗传算法来优化参数时,支持向量机预测性能最好,MSE达到5.398。
5 结论
本文在分析指数平滑法预测备件需求量的基础上,通过引入SVM理论,构建了相应的备件需求预测模型,并利用遗传算法和网络搜索法对实例数据进行计算。通过三种方法对比分析,支持SVM模型预测精度远高于指数平滑法,且利用遗传算法优化后的SVM模型精度更高,说明本文所研究的方法能够有效解决装备备件小样本预测问题。下一步将对SVM的应用开展进一步研究,特别是选取不同核函数对预测结果的影响。
参考文献:
[1] 王金鹏,沈顺成.现代航材管理理念在我军航材管理上的应用[J].中国水运,2007,7(2):177-178.
[2] 程玉波,车建国,杨作宾,等.基于指数平滑法的装备维修器材需求量预测[J].指挥控制与仿真,2009,31(1):115-117.
[3] 王斌,王勤为,董科,等.基于二次指数平滑预测的虚拟机调度方法研究[J].计算机应用研究,2017,34(3):723-726.
[4] 夏贵进,张曦,张居梅,等.基于三次指数平滑法的光纤损耗预测研究[J].光通信技术,2014(1):90-94.
[5] 商兴华,马燕妮.航材可修件备用量需求优化研究[J].兵工自动化,2016(1):83-85.
[6] 姜晨,徐廷学,余仁波.基于DAGSVM的装备不常用备件分类方法[J].舰船科学技术,2011,33(7):135-139.
[7] 段鹏飞,周绍骑.支持向量机在装备维修备件需求量预测中的应用[J].物流科技,2010(4):67-69.
[8] 王文.基于支持向量机的不常用备件需求预测方法研究[D].武汉:华中科技大学,2006.
[9] 冯杨,尹迪,罗兵.基于LS-SVM的间断性需求备件预测[J].舰船电子工程,2010(6):67-69.
[10] TONG X.W,HU T,CUI H.J.Hazard regression with penalized spline:the smoothing parameter choice and asymptotics[J].Acta Mathematica Scientia,2010,30B(5):1759-1756.
[11] 金旭星,盛奎川.指数平滑参数与初值的选取研究[J].江南大学学报(自然科学版),2005,4(3):316-319.
[12] GAO J B,GUNN S R,HARRRIS C J,et al.A probabilistic Framework for SVM Regression and Error Bar Estimation[J].Machine Learning,2002:46(3):71-89.
[13] MYASNIKOVA E,SAMSONOVA A,SAMSONOVA M R J.Support vector regression applied to the determination of the developmental age of a drosophila embryo from its segementation gene expression patterns[J].Bioinformatics,2002,18:87-95.
[14] CHUN H W,JAN M H,LEE D T.Travel-time Prediction with support Vector[J].Regression.IEEE Transaction on Intelligent Transportation Systems,2004:5(4):276-281.
[15] 白鹏,张斌.支持向量机理论及工程应用实例[M].西安:西安电子科技大学出版社,2008:50-61.
[16] KREBEL U.Pairwise classification and support vector machines[C]//Schuolkopf B,Burges C J C,Smola A J.Advances in Kernel Methods:Support Vector Learning,pages,MIT Press,Cambridge,MA,1999:255-268.
[17] HYNDMAN R J. KOEHLER A B,SNYDER R D,et al.A state space framework for automatic forecasting using exponential smoothing methods[J].International Journal of Forecasting,2002:18(3):439-454.
[18] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,2000:33-46.
[19] 龚纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,2010:313-343.
[20] 卞艺杰,李杭. 基于 GM(1,1)模型的南京市电力需求预测与探究[J].重庆理工大学学报(自然科学),2016(7):69-73.

