基于梁单元和板壳单元混合建模的折叠椅轻量化设计
周美施,尹怀仙,张铁柱,张洪信,王楠
(青岛大学 机电工程学院,山东 青岛 266071)
0 引言
现今折叠椅生产企业越来越多,竞争愈发激烈,减轻折叠椅生产成本成为增强企业核心竞争力的关键。折叠椅骨架是主要承载构件,对其骨架结构进行轻量化设计,可以节省材料,降低折叠椅生产成本。目前对于折叠椅的有限元分析以及优化设计研究还相对较少。目前产品结构设计方法,主要有拓扑优化和尺寸优化,其中拓扑优化主要应用于产品开发设计阶段,对于已经成熟的产品结构没有太大的实际意义[1-3],因此本文对某折叠椅产品结构采用尺寸优化设计,减轻折叠椅质量。
传统的尺寸优化用壳单元模拟折叠椅结构,再针对其壳单元厚度进行尺寸优化,有一定效果,但建模复杂。由于厚度的变化,特别是管件厚度的变化受管件基本管径的约束,其变化的维度和方向受限,优化效果也受限制。而采用梁单元模拟管件,可以对梁单元管径和厚度进行优化设计,能在比较大的变量空间寻得最优解,优化效果更好[4-6]。
1 折叠椅有限元模型的建立
折叠椅骨架由材料为Q345的空心圆管、方管组成,Q345弹性模量为2.06×1011MPa,泊松比为0.28,密度为7 850 kg/m3,屈服强度为345 MPa。椅面材料为尼龙布,弹性模量为2.83×109MPa,泊松比为0.4,密度为1 100 kg/m3。通过对折叠椅结构力学特征和结构特征进行分析研究,在ANSYS中建立折叠椅有限元模型,其中折叠椅骨架结构由梁单元模拟,椅面采用壳单元模拟,对折叠椅进行网格划分,折叠椅有限元模型共有3 614个单元,3 484个节点。折叠椅的有限元模型如图1所示。
根据调查显示折叠椅在极限姿态下所受应力最大,因此对折叠在极限姿态下的模型进行有限元分析,其中假设114kg的重物从离椅面40cm高位置自由落体,从接触椅面到静止所用时间为0.2s,根据冲量定理计算椅面所受冲击载荷为1 718N。载荷均布加载到椅面所在节点(图2)。在有限元计算中,需要消除节点的刚性位移保证刚度矩阵的非奇异,求解出刚度位移矩阵,得到正确的数值解[7-8]。因此需要对折叠椅的模型施加正确的自由度约束,对折叠椅腿与地面接触的2根矩形梁所在节点施加固定约束。
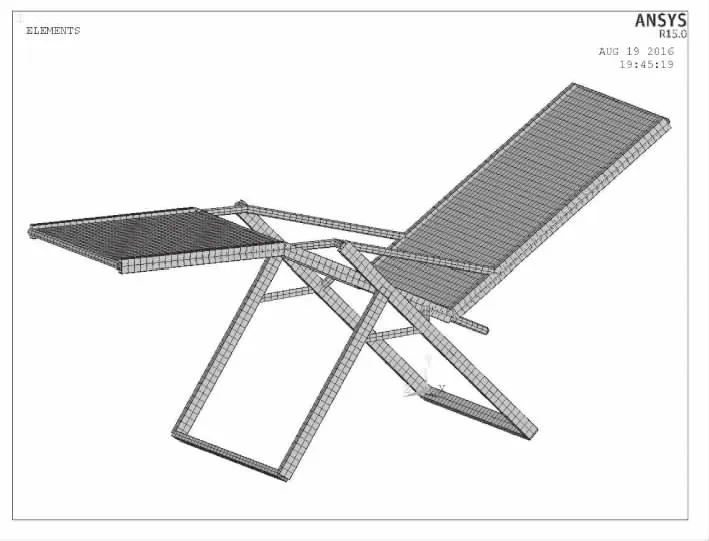
图1 折叠椅有限元模型

图2 约束和加载
2 有限元分析结果
通过有限元计算得到折叠椅有限元模型在极限姿态下的应力结果和变形结果。其等效应力云图如图3所示,变形云图如图4所示。最大等效应力为114MPa,最大应力节点出现在左后支腿与矩横梁连接位置,与企业实验得到破坏点一致,验证了次折叠椅有限元模型的正确性。从折叠椅等效应力云图可以看出椅面拐角骨架连接处有较小应力较高区域,如图5所示,其值约为150MPa左右,折叠椅骨架其他部分应力值都较低,根据材料力学中强度公式[9]。对于弹塑性材料,许用应力可用下列公式求解。
σ=σs/n
式中,σ代表折叠椅的许用应力,σs代表Q345的屈服强度,n代表材料的安全系数,其中取n=1.3,Q345的屈服强度为345MPa,因此可以得出折叠椅的许用应力为265MPa。
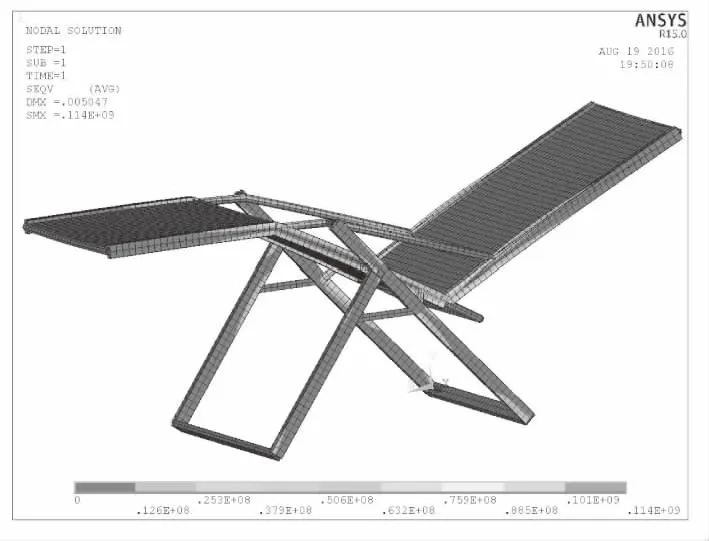
图3 折叠椅应力云图
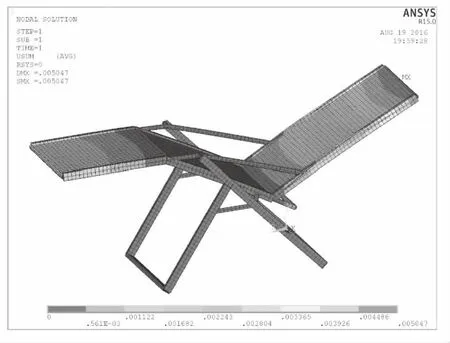
图4 折叠椅变形云图
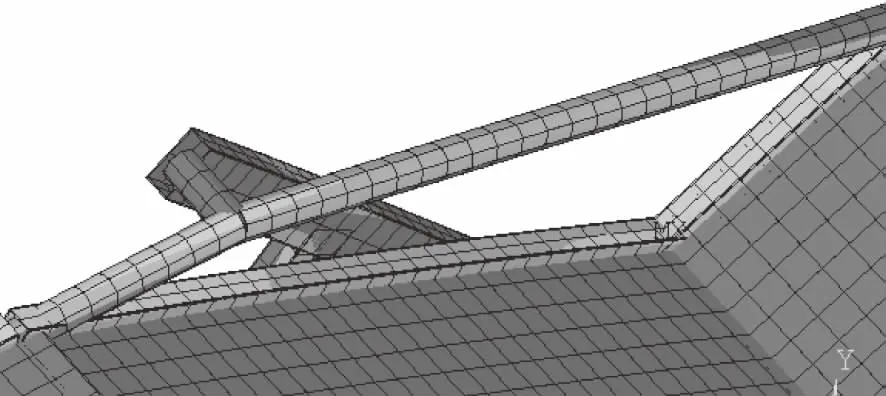
图5 骨架应力较高区域局部放大图
通过有限元计算与折叠椅的许用应力值对比可知,折叠椅骨架结构存在较大的强度冗余,可对折叠椅进行轻量化设计,增加材料使用率,降低生产成本。
3 轻量化设计
以折叠椅骨架质量最小作为优化目标。
折叠椅骨架主要由截面尺寸为38×18mm,壁厚为0.9mm的空心方管和外径为11mm,壁厚为1.1mm的空心圆管组成,选取空心方管的壁厚W1,空心圆管外径D1和空心圆管壁厚T1作为设计变量。设定空心方管壁厚变化范围为0.4mm~1mm,空心圆管外径变换范围为12mm~40mm,空心圆管壁厚变化范围为0.6mm~3mm。
约束条件选取折叠椅骨架最大等效应力小于折叠椅许用应力,折叠椅骨架最大变形小于许用变形δ,其中δ=50mm。
折叠椅轻量化设计的数学模型为:
利用Isight集成ANSYS,在Isight中设定好参数,利用全局优化算法[10]进行优化计算,优化迭代1 001次,完成优化计算,表1为优化前后各设计变量数值。图6为优化计算目标函数迭代曲线。优化后折叠椅骨架质量为5.88 kg,优化前折叠椅骨架质量为11.36 kg,通过优化设计折叠椅骨架质量减轻48.24%,达到轻量化设计要求。
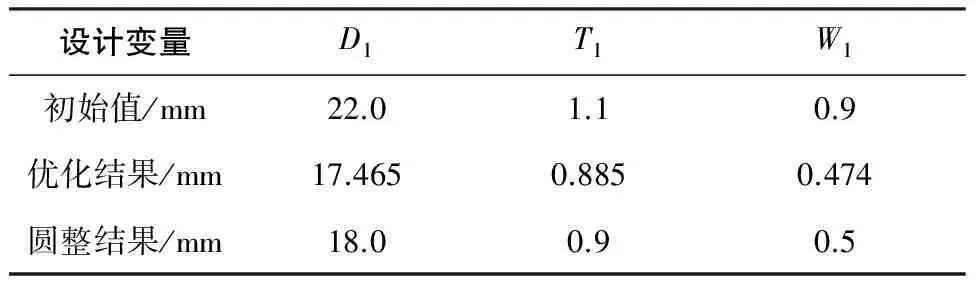
表1 优化前后各设计变量数值
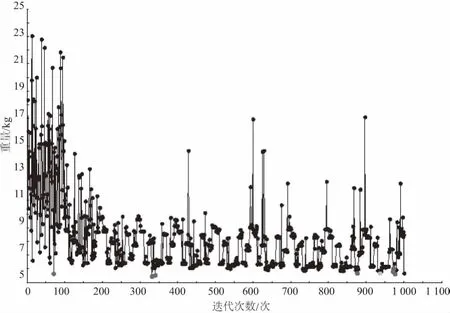
图6 目标函数迭代曲线
考虑加工工艺以及加工成本的需要,按圆整优化后各设计变量结果重建折叠椅有限元模型,得到圆整后折叠椅骨架质量为6.73kg,比优化前质量减轻40%。再次进行折叠椅有限元计算,得到优化后折叠椅有限元模型的应力云图和变形云图如图7和图8所示。其中折叠椅的最大等效应力为263.73MPa,小于折叠椅许用应力,最大变形为13mm小于许用变形值,说明优化后折叠椅结构满足强度、刚度要求,本次优化设计是可行的。
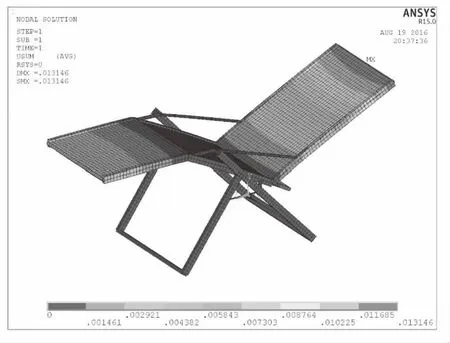
图7 优化后折叠椅应力云图
4 结语
1) 建立折叠椅的有限元模型,应用有限元分析方法
获得折叠椅在极限姿态下的应力分布情况,在此基础上,以折叠椅主要构件的截面尺寸为设计变量,以强度、刚度为约束条件,以折叠椅质量最轻为优化目标,对其进行尺寸优化设计,优化后折叠椅的质量减轻了40%,达到了轻量化的优化目标。
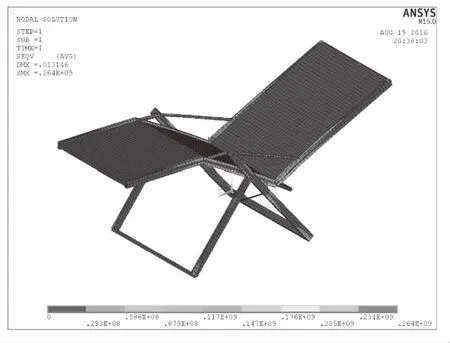
图8 优化后折叠椅变形云图
2) 提供了一种基于梁、板壳单元的折叠椅有限元建模方法,相比单利用壳体单元建模,增加折叠椅在较大的维度和方向上寻优,使得轻量化效果更为明显。
3) 为折叠椅结构改进提供了一种行之有效的优化方法。
参考文献:
[1] 马骊溟,朱智民,李伟光,等. 满意度动态加权法在自卸车车架拓扑优化中的应用[J]. 解放军理工大学学报(自然科学版),2013,14(4):436-440.
[2] 张君媛,徐婷婷,张秋实,等. 长纤维复合材料乘用车后排座椅骨架轻量化设计[J]. 汽车技术,2015(8):10-13.
[3] 张坤,丁晓红,倪维宇,等. 汽车座椅骨架构件布局设计方法[J]. 工程设计学报,2015(2):166-171.
[4] 贺岩松,黄深荣,张志飞,等. 摩托车车架基于梁单元的结构优化[J]. 机械科学与技术,2013,32(12):1748-1751.
[5] 哈斯巴根,朱凌,石琴,等. 轮胎有限元建模过程优化及刚度特性仿真研究[J]. 合肥工业大学学报(自然科学版),2015(7):944-948.
[6] 刘照麟. 基于梁单元重要性的杆件结构优化方法及应用研究[D]. 桂林:桂林电子科技大学,2014.
[7] 赵韩,钱德猛. 基于ANSYS的汽车结构轻量化设计[J]. 农业机械学报,2005,36(6):12-15.
[8] 唐进元,蒲太平. 基于有限元法的螺旋锥齿轮啮合刚度计算[J]. 机械工程学报,2011,47(11):23-29.
[9] 刘鸿文. 材料力学[M]. 北京:高等教育出版社,2004.
[10] 韩志强. 某发射装置上架的减重技术研究[D]. 南京:南京理工大学,2006.

