基于灵敏度分析的动车组转向架模型修正

贺斐洋，史治宇

(南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016)

0 引言

转向架是机车车辆最重要的组成部件之一，其结构是否合理直接影响机车车辆的运行品质、动力性能和行车安全。转向架技术是靠轮轨接触运行的现代机车得以生存发展的核心技术之一。转向架主要用于承受动车组的质量，并把轮轨接触处产生的轮周牵引力传递给车架牵引列车前进。当路面不够平整时缓冲路面带给列车的冲击；当铁轨转弯时引导列车顺利完成变向；当列车进站或者遇到紧急情况时能够产生制动力令列车停止。因此获得高精度的动车组转向架有限元模型对试验和生产都能够带来重要的指导意义。本文利用转向架模态试验的测试信息来修正初始有限元模型，使有限元模型和试验模型之间的误差在给定范围内达到最小，为后续的频响分析和疲劳分析提供了更加可靠的有限元模型，进一步提高了仿真的准确性。

根据修正对象的不同，模型修正方法可以划分为矩阵型修正方法[1]和参数型修正方法[2]两类。本文采用的修正方法是基于灵敏度分析的参数型修正法。其基本思路是通过构造理论模型与实际模型之间在相同条件下动力特性的误差，然后选择修正参数进行修正，使该误差最小化来达到修正的目的。其中，基于模态频率的修正方法修正精度较高，但试验模态技术通常只能获得结构低价模态特性，当修正参数较多时，方程亚定，Chen[3]对此类问题进行了研究。基于固有振型的修正，振型数据足够但识别精度较差，因此振型在模型修正中使用较少。基于模态置信度(MAC)的修正方法对噪声的敏感度小于振型，但可利用的数据数目同样不超过识别的模态数。Dascotte[4]对方程的性态问题做了深入研究，Friswell等[5-6]对基于模态参数的模型修正方法各个方面问题进行了研究，以推动模型修正技术向前发展。

本文通过MATLAB编程调用NASTRAN灵敏度计算分析结果，采用二次规划优化算法，以模型材料的弹性模量和模型各主要部分壳单元的厚度为修正对象进行了模型修正。进而获得了高精度的动车组转向架有限元模型。

1 模型修正理论

结构的有限元模型总共有n个设计参数，其中前m个为待修正的参数，设计参数可以表示为：

P=P1,P2…Pm…PnT

(1)

对应的特征量可以表示为：

f=FK,M=FfKp,fMp=fpp

(2)

其中f可以是结构任意的特征量，如模态频率、振型等。模型修正问题转化为如下的优化问题：

(3)

其中{fe}和{fpp}分别代表结构动态特性的试验值与分析值；Rp称之为残差项；VLB、VUB分别代表结构设计参数的上限和下限；而Wf代表结构各个特征量之间的加权矩阵。

一般情况下，{fpp}是设计参数的非线性函数。为了将非线性问题转化为线性问题，在初始设计点将{fpp}对待修正参数进行一阶泰勒展开为：

fpp=fpp0+SΔP

(4)

式中p0是设计参数初始值。

(5)

S代表结构特征量对设计参数的灵敏度矩阵。Δp=p-p0代表设计参数的误差。利用拉各朗日乘数法，式(3)的极值问题转化为如下的线性问题。

WfSΔp=Wffe-fpp0

(6)

式(6)就是常见的模型修正方程，且是一个迭代优化的过程。具体过程如图1所示。

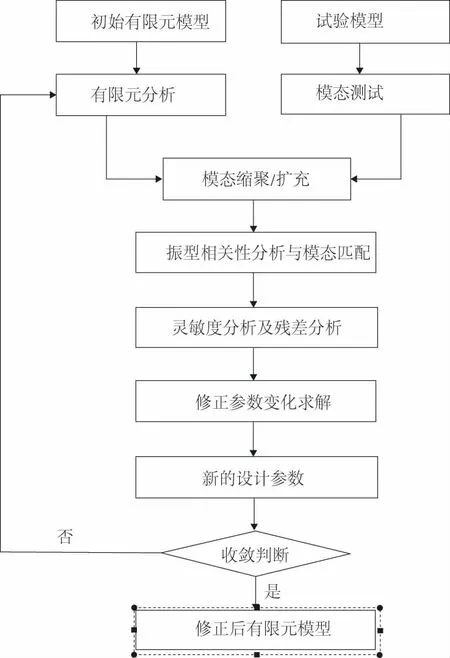
图1 模型修正流程图

2 灵敏度分析

本文中由于试验主要是得到了构件的固有频率和固有振型，所以重点介绍这两者的灵敏度[7]。特征值(固有频率的平方)的灵敏度可以直接获得解析式，在求解特征值灵敏度问题时，主要有2个重要的约束方程：特征方程和加权正交方程，即：

K-λrMφr=0

(7)

(8)

由式(7)和式(8)可推得结构的第r阶特征值对结构的第j个设计参数的导数为：

(9)

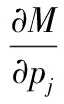
计算振型对设计参数的偏导数的典型方法是Nelson法。

令：

(10)

则：

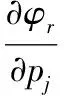
(11)

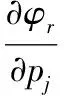
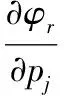
(12)

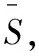
(13)

求得方程(11)的特解为：

(14)

(15)

将式(12)带入式(15)，得到：

(16)

这就求得模态振型关于设计参数的偏导数。

由于振型通常不作为修正目标，定义振型相关系数如下：第i阶试验振型与第j阶计算振型的振型相关系数即模态置信度MAC计算式为：

(17)

MAC值是一个介于0～1之间的量，MAC=1代表试验振型和有限元振型完全匹配，MAC=0代表试验振型和有限元振型完全不相关。将式(17)两端对结构的第n个设计参数求导得：

(18)

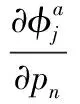
3 动车组转向架模型修正

3.1 模型介绍

动车组转向架有限元建模包括轮对、构架等关键部件，以及转向架各部件之间的连接。本文仅对转向架构架建立缩比模型，并对其进行了一定简化。该构架长700mm，宽780mm，高85mm，总重22.8kg。主体结构为钢制，不同部件通过焊接相连。构架模型如图2所示,A处是左右对称的2根等强度承重侧梁，这是转向架的主要承力构件，受力部分主要集中在侧梁两端的耳片上。B处是2根等截面横梁，这是构架的主要连接部件，C处代表左右2根空气弹簧梁，D处代表6个刹车悬挂板、E处代表2根纵向连接梁、F处代表2个齿轮盒。其中A，C，D，E，F都通过焊接的方法连接在横梁B上。

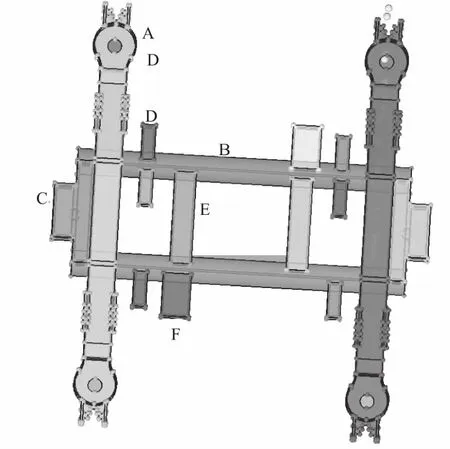
图2 动车组转向架模型

构架主要由薄壁结构组成，所以选用壳单元建模。首先在建模时，对模型进行几何处理，把倒角、圆角部分去除，一些次要边界、影响不大的细小孔洞、凹坑直接填满，使模型表面尽量光滑，以保证网格质量。之后抽取中面，抽取中面的过程中把厚度接近的部分赋予同一种属性，由于这些厚度属性所代表的薄壁部分经过了建模简化和几何处理，并不是严格意义上的等厚度，所以这些壳单元的厚度属性是主要修正目标。针对转向架模型，共设置了10个壳单元属性，如图3所示，图中不同的颜色代表不同的厚度属性。其中，由于左右2根侧梁是转向架的主要承力构件，所以属性的划分比较细致。侧梁截面上下板厚度、左右板厚度，侧梁两端截面厚度，侧梁两端耳片厚度，以及侧梁上表面突出的4个连接件厚度(绿色部分)分别赋予属性。另外2根横梁赋予一个属性，2个空气弹簧梁赋予一个属性，纵向连接梁，刹车悬挂板和齿轮盒赋予一个属性(本刊为黑白印刷，文中有色部分如有疑问，可咨询作者，下同)。

在四年的时间里，李丽经常和师兄师姐联系，并在假期的时候去他们的公司实习。很快所有的师兄师姐都喜欢上了这个勤奋爱学的师妹。李丽在师兄师姐的指导下，也学到了很多知识。在大四上半学期，当别的同学还在四处为工作奔波的时候，李丽已经接到了好几个师兄师姐入职的邀请。

图3 动车组转向架属性图

3.2 修正参数筛选

建立好初始有限元模型后，在Nastran中对转向架构架有限元模型进行模态分析。有限元模态分析和试验分析的匹配情况如图4所示。

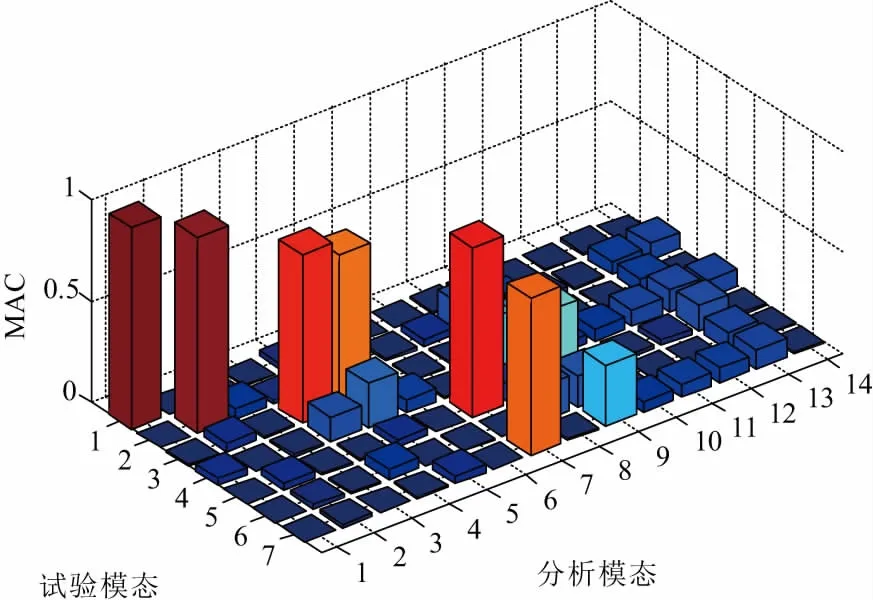
图4 构架模型试验/有限元模态匹配图

计算所有厚度属性以及材料杨氏模量的灵敏度，筛选其中灵敏度较大的量进行修正，最后确定了6个待修正参数，如表1所示。可以看出，影响转向架固有特性的量主要集中在侧梁和横梁上，而试验中用以测量振型的测点也主要布置在横梁和侧梁上，试验与有限元分析的结果相互吻合。

3.3 模型修正计算与分析

设置加权方法为：Wλ=0.8,WMAC=0.2。以1∶7阶固有频率和1∶7阶MAC值为目标，对转向架构架进行模型修正。修正结果如图5-图9所示。

表1 待修正参数

图5表示的是各个参数的倍数随着迭代步数增加的变化情况。因此修正之后，各参数的修正值是表1中各参数的初始值乘以图5中各参数最后一步的迭代结果。图6表示的是前7阶有限元分析模态频率和试验分析模态频率的误差随着迭代步数增加的变化关系。结合表2可以看出，修正前，模态频率最大误差是：11.8 %，最小误差：1.1 %，平均误差：5.3%。修正后，模态频率最大误差：3.8%，最小误差：0.2%，平均误差：2.0%。除了第1阶模态频率误差略有增大，其余阶次的模态频率误差都减小了。

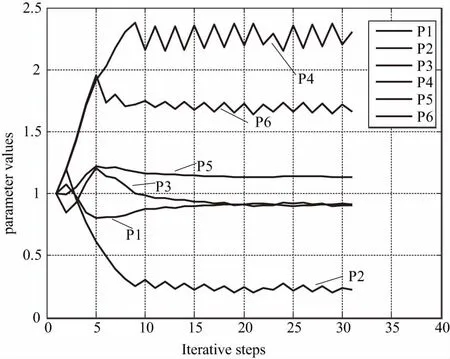
图5 参数收敛图(P1至P6依次代表表1中 从上到下第1至6个参数)

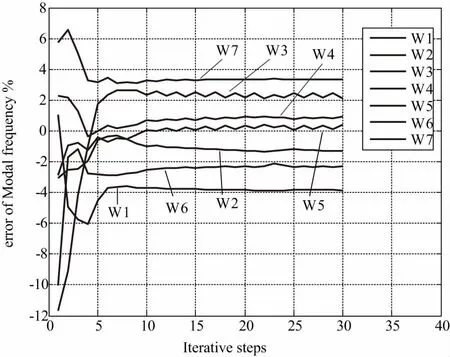
图6 前7阶模态频率收敛图(W1至W7依次表示 第1至第7阶固有频率)

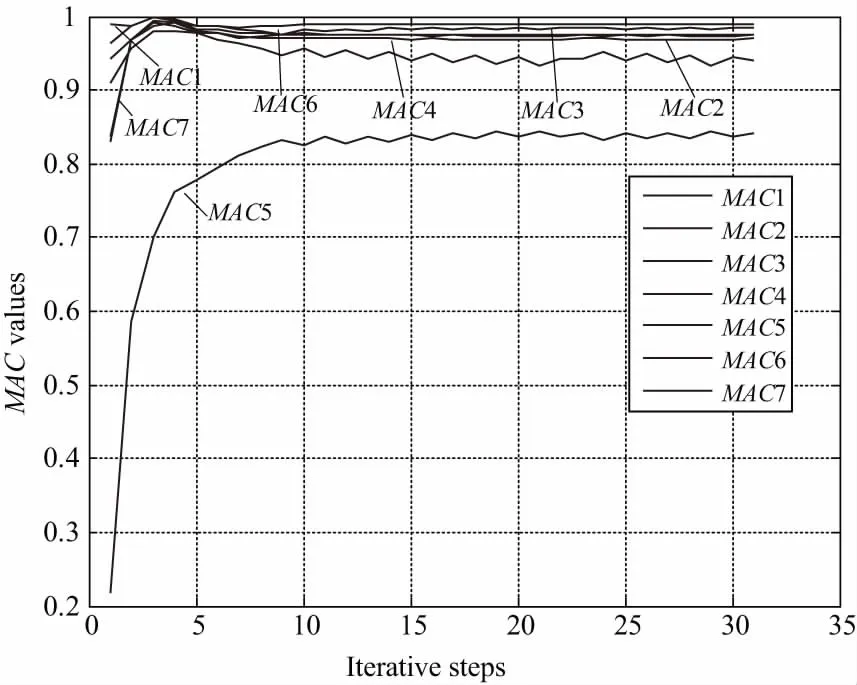
图7 MAC值收敛图(MAC1至MAC7依次表示 第1至7阶MAC值)

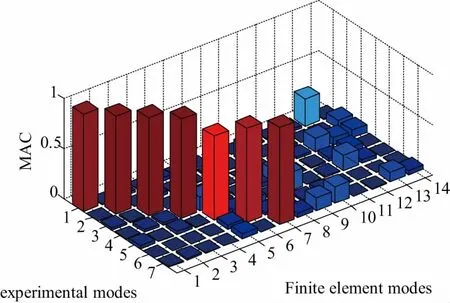
图8 修正后试验/有限元模型模态匹配图

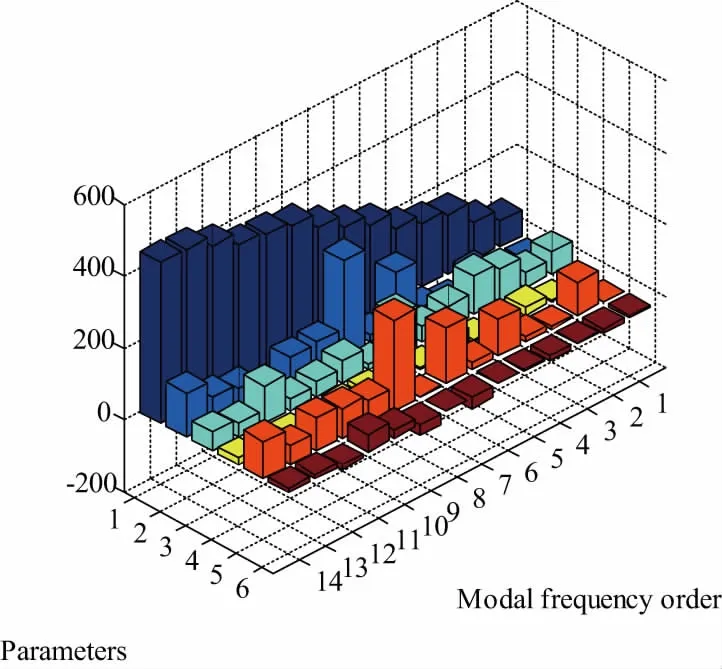
图9 灵敏度矩阵图

模型修正显著减小了模态频率的误差。图7表示的是前7阶MAC值随着迭代步数增加的变化关系。可以看出除了第5阶MAC值外其余MAC值都在0.9以上，第5阶MAC值也在0.8以上。前7阶有限元振型和试验振型匹配良好。图4和图8分别表示修改前后有限元模型和试验模型的模态匹配情况。可以发现，修正后模态匹配关系显著改善。图9表示的是有限元分析模态频率对各个参数的灵敏度。第1个参数的灵敏度最大，代表的是材料的弹性模量，其他的参数代表的都是壳单元的厚度。由于弹性模量的变化影响到所有单元的刚度矩阵，而壳单元厚度的变化只会影响到部分单元的刚度矩阵，所以第1个参数的灵敏度显著大于其他参数。另外，材料弹性模量一般可以通过试验获得，是比较可靠的数据，在模型修正中一般不产生变化，从图5中可以看出，参数1基本在1附近，变化很小。其余修正参数都代表各个部分壳单元的厚度，由于几何模型是通过抽中面的方式生成的，而模型各个部分并不是严格意义上的等厚度，所以其余参数的波动很明显。

转向架有限元模型和试验模型的差别主要在于有限元模型在建模过程中，为了保证网格的质量，会对工程结构中的孔槽、倒角、凹痕等结构进行几何处理、简化。另外各部件之间的连接方式也是产生差异的关键所在，试验模型中各个零件之间是焊接在一起的，而有限元模型中各零件之间是通过节点对节点的方式刚接在一起的，这样就不可避免地产生了误差。而通常对试验件进行模态分析又是必不可少的试验过程，所以用试验数据来修正有限元模型，为之后的频响分析、疲劳分析、损伤诊断等提供更加可靠的有限元模型是十分有必要的。

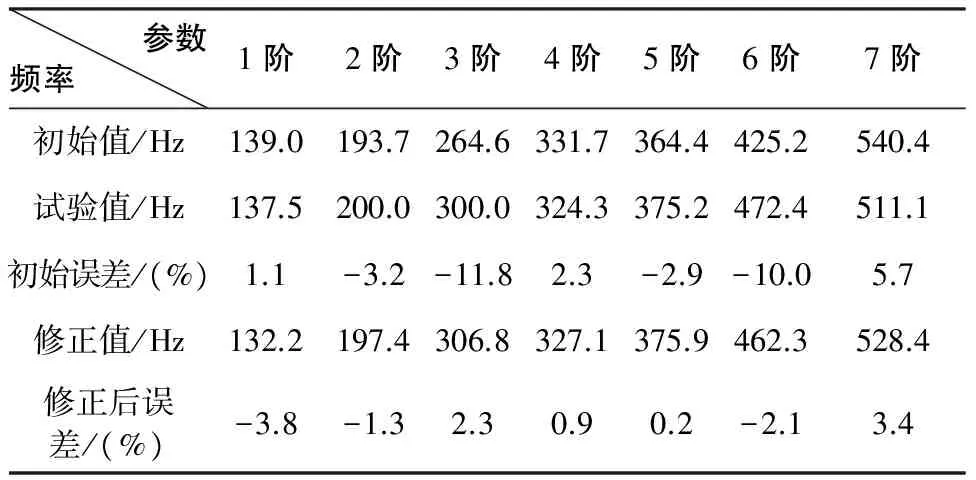
表2 模态频率初始值、修正值与目标频率对比

4 结语

本文基于灵敏度分析的模型修正方法对动车组转向架模型进行了模型修正。

1) 对基于灵敏度分析的模型修正技术进行了归纳和总结，介绍了振型相关分析，模态频率、模态振型和振型相关系数的灵敏度计算方法。

2) 本文利用Nastran可靠的模态分析和灵敏度分析功能，在Matlab的GUI平台上开发了模型修正软件ModelUpdating。

3) 基于灵敏度分析，运用模型修正软件ModelUpdating对动车组转向架模型进行了模型修正。修正之后，有限元模型前7阶频率与试验值的误差在5%以内，前7阶振型匹配良好，结构的固有特性能够收敛到试验模态，能够反映结构的振动特性，修正后的有限元模型满足工程精度需求。相比于初始有限元模型，修正后的动车组转向架有限元模型为工程上的进一步研究，诸如损伤诊断、疲劳分析等，提供了更高精度的有限元模型，对往后的试验和工程应用具有指导作用，可以减少试验成本。

参考文献:

[1] Wei F S. Stiffness matrix correction from incomplete test data[J]. AIAA,1980, 18(10): 1274-1275.

[2] Fox R L, Kapoor M P. Rates of change of eigenvalues and eigenvectors[J]. AIAA, 1968, 6(12): 2426-2429.

[3] Chen J. C, Garba J. A. Analytical Model Improvement Using Modal Test Results[J]. Journal of AIAA. 1980, 18(6):684-690.

[4] DascotteE, Strobbe J, Hua H. Sensitivity-based Model Updating Using Multiple Types of Simultaneous State Variables[J]. Proceeding of IMAC, 1995,2460(6):97-101.

[5] Mottershead J.E, Mares C, Friswell M.I. Selection and Updating of Parameters for an Aluminum Space-frame Model[J]. Mechanical System and Signal Processing, 2000,14(6):923-944.

[6] PrellsU, Friswell M.I. Application of the Variable Projection Method for Updating Models of Mechanical Systems[J]. Journal of sound and Vibration,1999,222(5):307-325.

[7] 李效法. 基于灵敏度分析的模型修正研究及其实现[D]. 南京：南京航空航天大学，2007.