乘积元素h1g0相关的Ext群

边俊鹏，王玉玉

(天津师范大学 数学科学学院，天津 300387)

令A为mod p Steenrod代数(p＞2)，P为A的由循环缩减幂p(ii≥0)生成的子代数.目前，低维球面稳定同伦群的计算进展较慢，且尚未有任何规律可循.从另一个角度来看，对于与球谱密切相关的Smith-Toda谱同伦群的非平凡元的研究就显得尤为重要，而对Smith-Toda谱上同调群的探究是发掘其同伦群非平凡元的必经之路，且仍然有大量未解决的问题.相关的结果请参见文献[1-5].本文考虑与h1g0相关的Ext群结果，得到

其中：r＞2，p＞7，q=2(p-1)，n=1、2.

Smith-Toda谱 V(n)的 Zp上同调群为 H*V(n)≌E[Q0，Q1，…，Qn]，其中Q(ii=0，…，n)是mod p Steenrod代数A的Minlor基元，E[]为外代数.由文献[6]，当 n=1、2、3且 p＞ 2n时，V(n)是可实现的，并且存在上纤维序列(V(-1)=S)

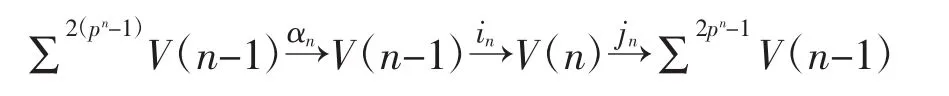
其中当 n=0、1、2、3 时 αn分别为 p、α、β、γ.此上纤维序列可以导出Zp上同调群的短正合序列，因此可导出下面的Ext群长正合序列

1 V(2)谱中的 Ext群

命题[7]，其中

推论

引理1当r≥2，p≥7时，Zp)=0.

证明由推论，并根据文献[6]的引理2.2可知

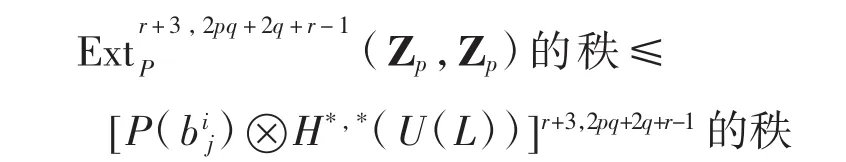
由文献[8]，当 t-r＜(p3+3p2+2p+1)q-4时，Hr，t(U(L))由以下上同调类(乘法)所生成

并且对于加法有

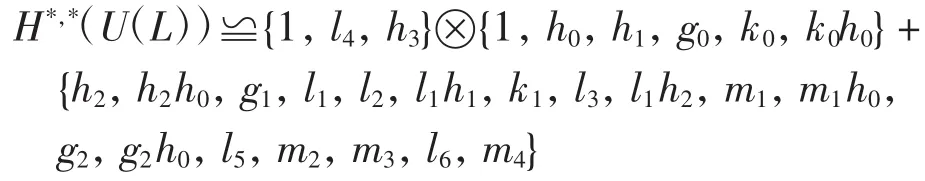
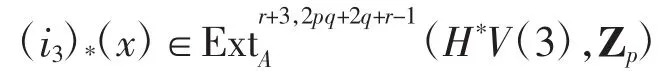
此时(i3)(*x)的全次数为2pq+2q-4≡2q mod pq-2.

由λ和λ*可知x可能为g0，对应全次数为pq+2q-2，而(i3)(*x)的全次数为2pq+2q-4，二者不相等，故(i3)(*x)=0.考虑下面长正合序列

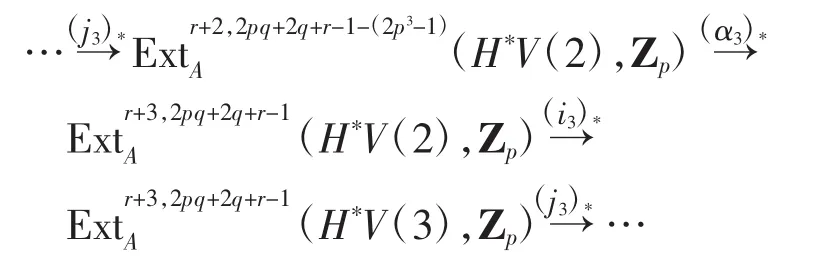
因此存在

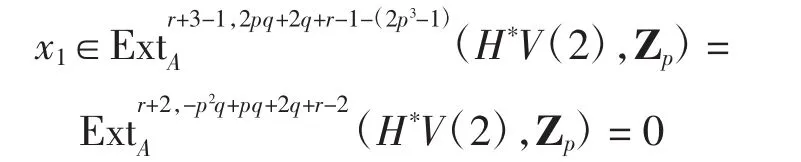
满足x=(α3)(*x1)=0，即

引理2当r≥2，p≥7时，Zp)=0.

证明当r≥3时，引理恒成立.下面仅考虑r=2的情况.

由正合性，存在

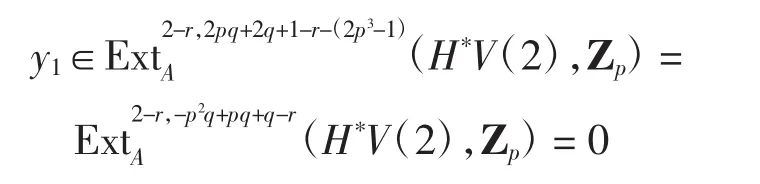
满足y=(α3)(*y1)=0，即

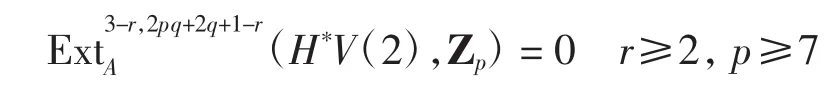
2 V(1)谱中的 Ext群

定理1当r≥2，p≥7时，Zp)=0.

证明由推论知

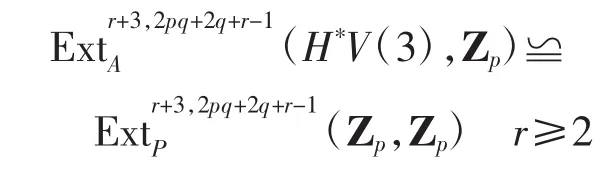
将[P(bi)j⊗H*，(*U(L))]r，t中全次数不大于2pq+2q-4的生成元记为λ，其全次数mod pq-2后的余数记为λ*，λ 和 λ*如下：

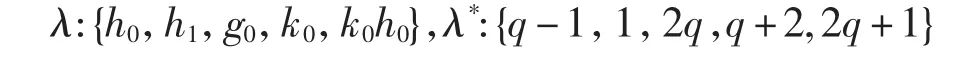
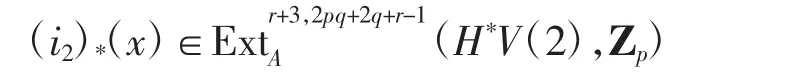
由下面的长正合序列

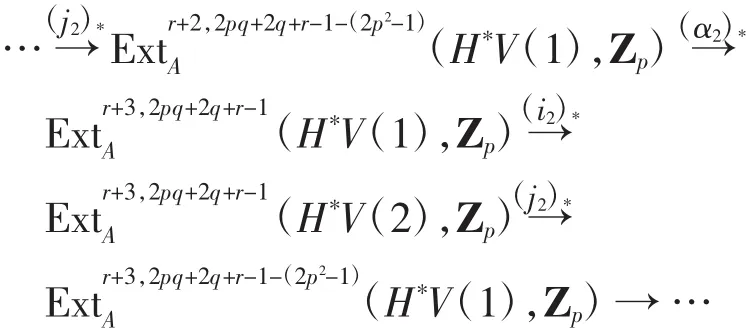
存在

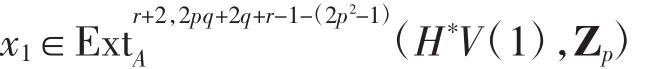
满足(α2)(*x1)=x.由正合性知存在

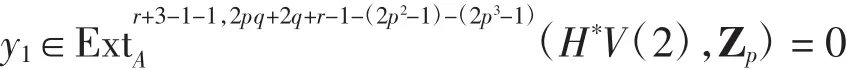
满足(α3)(*y1)=(i2)(*x1)=0.

同理，存在

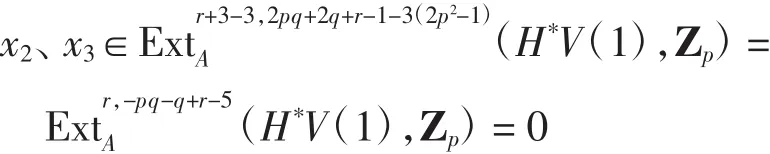
满足x=(α2)(*α2)(*α2)(*x3).因此x=(α2)(*α2)(*α2)*(x3)=0，即

定理2当r≥2，p≥7时，Ext3-r，2pq+2q+1-(rH*V(1)，AZp)=0.

证明当r≥3时，定理显然成立.下面仅考虑r=2的情形.

由引理2有

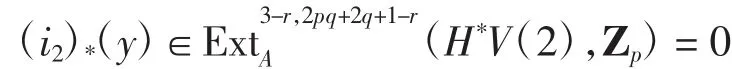
由正合性，存在

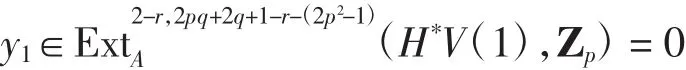
满足(α2)(*y1)=y=0.从而

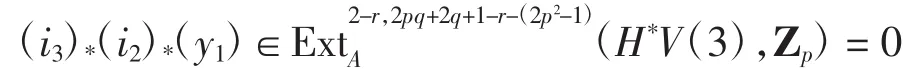
因此(i2)(*y1)=(α3)(*y′)=0，其中

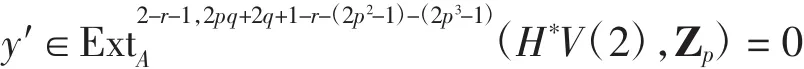
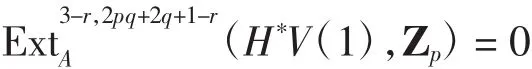
注1定理1与定理2可以为探究h1g0在谱V(1)同伦群的收敛性提供有力的依据.

注2由于中的可分解元素有kh=00?h1g0，因此本文的结论同样适用于对k0h0收敛性的讨论.

参考文献：

[1]ZHONG L N，WANG Y Y.Detection of a nontrivial product in the stable homotopy groups of spheres[J].AlgebraicandGeometricTopology，2013，13(5)：3009-3029.

[2]王玉玉，王健波.球面稳定同伦群中的ξn-相关元素的非平凡性[J].数学年刊，2014，35(5)：575-582.WANG Y Y，WANG J B.The non-triviality of ξn-related elements in thestablehomotopygroupsofsphere[J].Chinese Annals of Mathematics，2014，35(5)：575-582(in Chinese).

[3]WANG Y Y，WANG J B.The non-triviality of ζn-related elements in the stable homotopy groups of sphere[J].Mathematica Scandinavica，2015，117(2)：304-319.

[4]钟立楠，刘秀贵.Adams谱序列上的非平凡乘积b0k0δ軇s+4[J].数学物理学报，2014，34(2)：274-282.ZHONG L N，LIU X G.Non-triviality of the product b0k0δ軇s+4in the Adams spectral sequence[J].Acta Mathematica Scientia，2014，34(2)：274-282(in Chinese).

[5]ZHONG L N，PIAO Y J.A nontrivial product in the May spectral sequence[J].Journal of Mathematical Research and Exposition，2011，31(2)：359-365.

[6]TODA H.On spectra realizing exterior part of the Steenrod algebra[J].Topology，1971，10(1)：53-65.

[7]王健波，肖建明.h0b31在π*V(1)中的收敛性[J].南开大学学报(自然科学版)，2006，39(1)：43-48.WANG J B，XIAO J M.The convergence of h0b31in π*V(1)[J].Acta Scientiarum Naturalium Universitatis Nankaiensis，2006，39(1)：43-48(in Chinese).

[8]MAY J P.The cohomology of restricted Lie algebra and Hopf algebra[J].Journal of Algebra，1966，3(2)：123-146.