基于过完备字典的视频压缩采集算法

段宏伟

(山西职业技术学院 数控系， 山西 太原 030006)

视频图像具有可压缩性和稀疏性， 它们可以在特定的正交基或框架下稀疏表示. 然而， 传统的成像系统是对视频图像的所有数据进行采集， 然后再对其进行压缩. 在这个过程中， 视频图像的稀疏性被忽略， 浪费了有限而宝贵的资源. 研究表明， 压缩感知(Compressive Sensing, CS)[1]理论具有开发视频图像方面的潜力， 该技术将视频信号的采集和压缩结合在一起， 并可直接获取压缩过的信号. 与传统的成像系统不同， 该技术致力于最小化信号冗余的采集， 从而提高了采样效率.

压缩感知已成功应用于视频采集中. 文献[2]提出了将2D小波变换CS应用到视频中的每一帧， 并提出了逐帧压缩采样的方法， 视频中的每一帧被视为独立的图像. 这种方法利用视频帧的空域冗余， 提高了视频的采样效率， 然而， 其未涉及视频的空域冗余. 为了解决这个问题， 文献[3]提出了帧间差异压缩感知的方法， 对相邻帧之间的差异而非原始帧进行测量. 这种方法的缺点是， 所有的帧之间存在依赖性， 如果某一帧没有得到很好的恢复， 重建误差会扩散到后面的视频帧， 甚至整个视频.

视频压缩感知的另一种方法为三维变换压缩感知， 将整个视频看作一个数据块， 对整个视频同时进行处理[2]. 这种方法可以有效利用视频中的空域和时域稀疏性. 为了获得更高的稀疏性， 文献[4]中提出了使用Li-MAT[5]作为稀疏基的视频压缩感知方法， 该算法利用视频相邻帧之间的运动补偿， 获得比其他常规的三维变换更高的稀疏度. 但是这种方法需要在多个尺度上计算相邻帧的运动矢量， 计算复杂度大. 为了利用有限的测量值进行自适应采样， 一种基于视频块的采样框架在文献[6-7]中被提出， 首先每一帧被划分成不重叠的小块， 然后根据小块的时域变化对其进行分类. 然而实施小块分类和不同的采样策略增加了算法的时间成本， 而且该算法对分类器的设计过于敏感.

由于视频在不同稀疏基上的稀疏性并不相同， 本文设计了一个新的基于过完备字典的视频压缩感知系统. 在这个框架下， 视频同样被分为时间-空间的小块， 为每个小块采集相同数量的测量值. 为了视频的有效重构， 系统使用K-SVD方法为视频块训练了一种严格稀疏的过完备字典， 这样视频块的时间-空间稀疏性可以得到最大化的利用， 从而保证视频的高质量恢复.

1 压缩感知

假设x∈RN是一个可以在某个正交基或框架上稀疏表示的信号，x=Ψα，α∈RN只有K≪N个非零项， 则x是一个在稀疏基Ψ上K稀疏的信号. 压缩感知允许对信号进行非相干测量，y=Φx在随机投影域对信号进行采集. 根据压缩感知理论， 为了从采样值y重建原始信号x， 需要对下列问题进行求解，

min‖α‖1s.t. ‖s-Φx‖2≤ε,(1)

式中： ‖·‖1表示l1范数；ε为一个正常数. 各国研究者已经提过很多不同的算法来解决这个问题， 如正交匹配追踪(OMP)[8]， 分段正交匹配追踪(StOMP)[9]和基追踪(BP)[10]等. 此外， 对于图像来讲， 另一种还原方法是最小变分法. 设x为一个向量化后的图像， 那么重构问题可以写为

(2)

其中，

‖x‖TV=

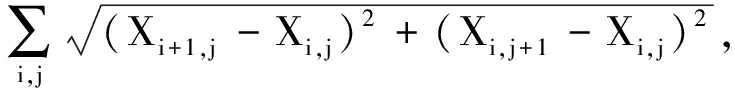
它可以看做图像l1范数的梯度.

2 视频压缩感知和过完备字典学习

不同于传统的视频采集系统， 本系统将视频采样和压缩结合在一起， 可以同时有效利用视频在空间和时间上的稀疏性. 此外， 所设计的算法还将视频场景内容的多样性和视频不同部分之间的差异性应用于过完备字典的自适应学习中.

2.1 框架

如图 1 所示， 视频中的每一帧图像被分为相同大小的n×n个不重叠的小块， 然后使用矩阵Φi对各个小块进行测量.

图 1 基于过完备字典的视频压缩感知结构图Fig.1 Block diagram of video compressive based on over-completed dictionary

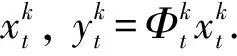
式中：Φ为测量矩阵.

2.2 视频块的过完备字典学习算法

本节讨论基于稀疏性约束的视频块过完备字典学习算法. 为了保证字典的通用性， 尽量使用具有复杂纹理和空域变化的视频块来对字典进行初始化， 本文选择了各种视频， 如运动的汽车， 流水， 骑马和其它不同的纹理变化. 在本文所设计的字典中， 任何视频的时间-空间小块都可以被表示为有限个字典元素的线性和.

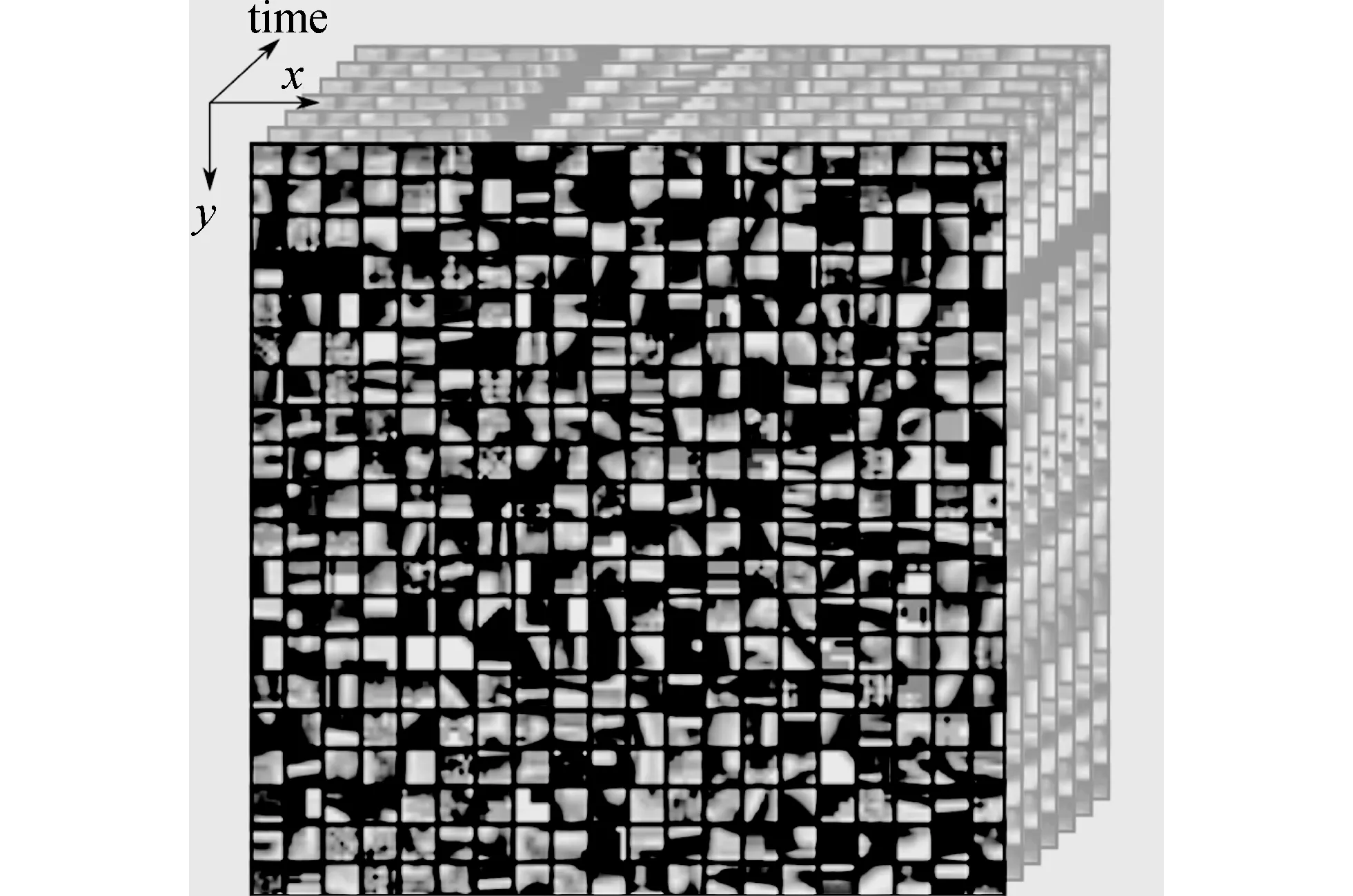
图 2 部分过完备稀疏字典Fig.2 Part of over-completed dictionary

在字典训练的初始阶段， 每个视频块都选自具有相同帧率的不同视频， 每个视频块被裁剪为大小8×8×8. 为了保证视频字典的多样性， 将每个视频字典原子进行8个方向的旋转并进行前向和后向的播放. 总共选择了100 000个原子作为初始字典并使用K-SVD训练方法[11]对字典进行训练， 图 2 展示了部分字典. 对于一个视频块E， 它将可以被表示为

E=Dα,(4)

式中：D为训练好的字典. 式(1)中所示的重构问题将变为

(5)

3 实验结果

为了测试系统的适应性， 实验在不同纹理复杂度和不同目标运动的视频上进行. 为了方便， 所有实验中的视频帧被裁剪为256×256， 它们被分割为8×8×8的时间-空间块. 使用采样比例来测量系统的有效性， 采样比例为测量值数目和总像素数目的比值. 实验对不同算法的视觉质量和峰值信噪比进行了比较， 每种算法都对相同的50个视频进行试验并计算出平均值. 对所有算法使用相同的采样比例和压缩感知重构算法， 系统使用“l1-magic”[12]工具箱中的内点法进行重构.

3.1 视觉质量比较

图 3 所示为不同采样比例下本文算法的重建结果. 很明显， 本文所提方法在即使测量比例低至5%的情况下依然可以获得令人满意的结果. 在采样比例逐渐提高的过程中， 重建结果获得了质量提升， 小块之间的不兼容性逐渐减少， 到达25%采样比例时几乎所有的块状效应都已经消失. 帧内部的纹理信息在低采样率的情况下依然可以得到较好的恢复.

图 3 不同采样比例下结果Fig.3 Visual comparison under different measurement ratio

图 4 和图 5 给出了在相同采样比例下不同算法的重构结果比较. 由于2.2节中所训练的字典可以使采集信号获得更高的稀疏性， 在相同的采样比例下， 本文算法可以获得比其他现有算法更加优秀的结果. 由图4可见， 本文算法可以有效恢复出视频的纹理和帧间的目标运动. 在采样比例为5%时本文算法虽有块状效应， 但基本轮廓和纹理信息可见， 其它算法很难辨别出恢复结果.

由图5可见， 在采样比例为25%时， 本文算法的结果基本为原图， 而其它算法的轮廓较为模糊， 内部纹理信息不如本文算法优秀.

图 4 采样比例为5%时不同算法相同采样比例下的结果Fig.4 Visual comparison for different methods when the measurement ratio is 5%

图 5 采样比例为25%时不同算法相同采样比例下的结果Fig.5 Visual comparison for different methods when the measurement ratio is 25%

3.2 不同方法的峰值信噪比

本节比较了相同采样比例下不同方法的峰值信噪比(PSNR). 使用了50个不同的视频作为实验对象并求平均值. 如图 6 所示， 本文算法达到了最好的PSNR， 尤其当采样率较低时， 由于采用稀疏基下的系数求解而后得到重构视频， 稀疏度的影响在此框架下非常重大.

三维视频字典的效率和效果非常明显， 远优于其他常规的标准正交基或分析基. 使用相同的测量值， 本文算法可以获得最少的误差， 同时可以获得最好的视觉质量.

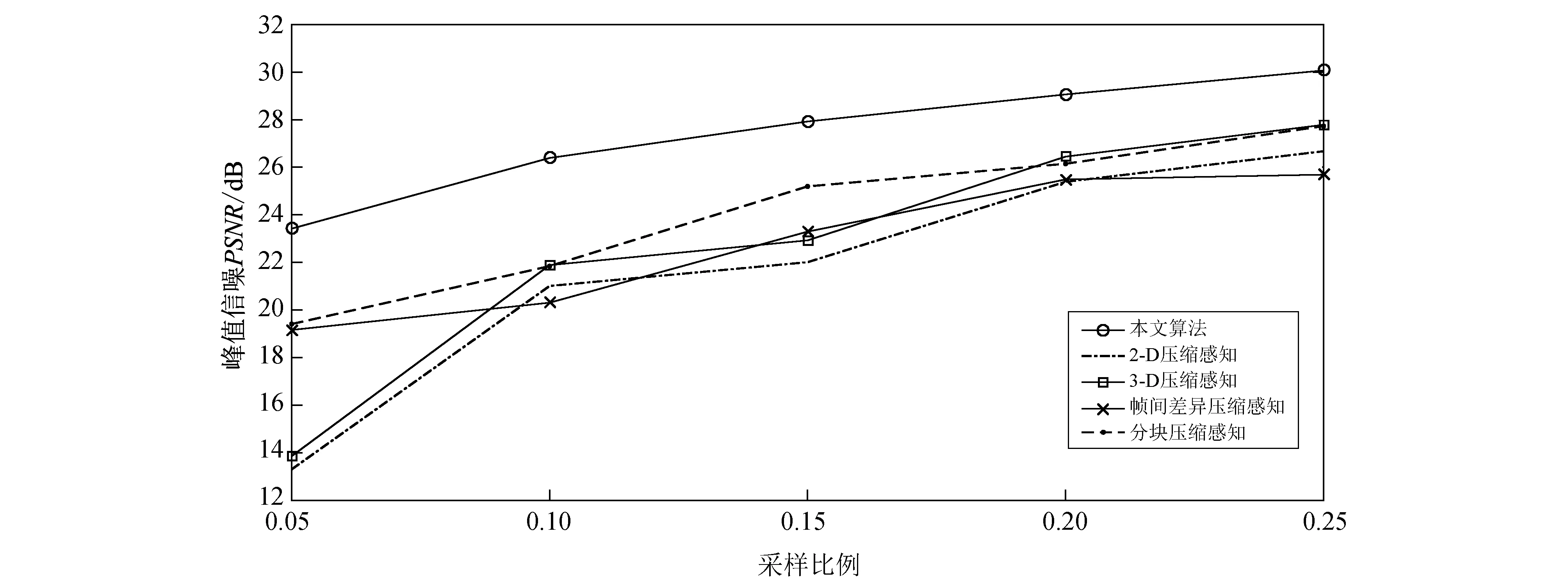
图 6 不同算法相同采样比例下的峰值信噪比比较Fig.6 PSNR of different methods under the same measurement ratio

4 结 论

本文提出了一种新的视频压缩感知系统， 该系统采用过完备字典作为稀疏基以获得更高的稀疏度. 在此框架下， 视频被分为不重叠的空间-时间小块， 并对其进行分别测量. 在重构阶段时间-空间小块可以进行联合重构， 实验表明重构结果在高稀疏度的影响下更加优化. 此外， 提出的视频压缩感知系统有效提高了视频的采样效率， 同时利用了视频时间和空间上的冗余， 在采样比例低至5%的情况下依然可以获得了令人满意的结果.

参考文献：

[1] Donoho D L. Compressive sensing[J]. IEEE Transactions on Information Theory, 2006, 52: 1289-1306.

[2] Wakin M, Laska J, Duarte M F, et al. Compressive imaging for video representation and coding[C]. Picture Coding Symp (PCS), Beijing, 2006: 716-731.

[3] Zheng J, Jacobs E L. Video compressive sensing using spatial domain sparsity[J]. Optical Engineering, 2010, 48(8): 1-10.

[4] Park J Y, Wakin M B. A multi-scale framework for compressive sensing of video[C]. Picture Coding Symp (PCS), Chicago, 2009: 1-4.

[5] Secker A, Taubman D. Lifting-based invertible motion adaptive transform framework for highly scalable video compression[J]. IEEE Transaction on Image Processing, 2003, 12(12): 1530-1542.

[6] Liu Z, Elezzabi A Y, Zhao H V, et al. Block-based adaptive compressed sensing for video[C]. IEEE International Conference on Image Processing (ICIP), HongKong, 2010: 133-142.

[7] Liu Z, Elezzabi A Y, Zhao H V, et al. Maximum frame rate video acquisition using adaptive compressed sensing[J]. IEEE Transaction on Circuits and Systems for Video Technology, 2011, 21(11): 1704-1718.

[8] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2008, 53(12): 4655-4666.

[9] Drori D D, Donoho D L, Tsaig Y， et al. Sparse solution of underdetermined linear equations by stage-wise orthogonal matching pursuit[C]. IEEE Transactions on Information Theory, 2012, 58: 1094-1121.

[10] Candes E, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[11] Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing over-complete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[12] Candes E, Romberg J. l1-magic: recovery of sparse signals via convex programming[EB/OL]. http:∥users.ece.gatech.edu/ justin/l1magic, 2011-10-11.