噪声协方差自适应控制下的双天线GNSS/INS初始对准方法

郝雨时，徐爱功，隋 心，王长强

辽宁工程技术大学，辽宁 阜新 123000

初始对准是捷联惯性导航系统(strapdown inertial navigation system，SINS)导航的重要环节，其对准精度直接影响后续导航精度。随着多源传感器组合导航技术的发展，GNSS(global navigation satellite system)/INS(inertial navigation system)组合导航及对准问题成为研究热点之一。GNSS可提供高精度位置和速度信息，但对准过程中单天线不提供姿态信息，姿态误差补偿能力受限。为此相关学者进行了探讨[1-4]，其中大部分双天线GNSS/INS初始对准方法均利用GNSS侧向结果辅助INS初始对准，忽略了GNSS观测噪声的影响。若两天线基线长度较短(如1 m)，基线平面精度2 cm，直接利用GNSS测向结果，最大可引入1.15°的航向角误差，不满足高精度测姿要求。因此，应从姿态误差模型角度出发，利用相关数据融合算法，不完全依赖GNSS测向结果辅助INS初始对准。

扩展卡尔曼滤波(extended Kalman filter，EKF)广泛应用于GNSS/INS组合导航数据处理，但大部分实际应用中，精确的数学模型、参数及噪声统计信息无法获取，仅采用EKF无法获取最优滤波解[5]。关于噪声特性未知情况下的Kalman滤波有Sage滤波[6-8]、基于方差分量估计的自适应滤波[9]、抗差自矫正Kalman滤波[10]等。关于控制异常误差影响的研究有抗差Kalman滤波[11]、自适应Kalman滤波和抗差自适应Kalman滤波[12-16]等。文献[8—11]提出将自适应滤波理论应用到GNSS/INS组合导航系统数据处理中，从不同角度对Kalman滤波进行了改进，取得了明显效果。关于异常控制方面的方法可以提高模型稳定性，并不意味着能完全提高姿态参数的绝对精度，绝对精度主要受观测值精度影响，需要相关观测噪声优化方法，以弱化低质量观测值对参数解算的影响。

针对上述问题，本文从系统噪声优化及观测噪声优化两方面对双天线GNSS/INS初始对准方法进行改进：优化系统噪声协方差，提升模型稳定性；优化GNSS观测噪声协方差，避免参数解算受较大观测噪声影响；通过分析天线间基线向量长度偏差，以偏差最小的基线向量解为观测值，进一步提高对准绝对精度，验证观测噪声优化的必要性。

本文首先说明双天线GNSS/INS组合导航初始对准模型，接着基于EKF说明系统噪声协方差自适应控制及观测噪声协方差自适应控制，然后利用试验，比较不同噪声自适应控制机制对对准模型稳定性及精度的影响。最后，总结本文所采用的基于噪声协方差自适应控制下双天线GNSS/INS初始对准方法优势。

1 双天线GNSS/INS初始对准

初始对准过程在静止基座上完成，并采用卡尔曼滤波实现最优初始对准和标定[5]。本文所讨论的双天线GNSS/INS初始对准模型结构如图1所示。本节介绍双天线GNSS/INS初始对准模型，包括系统模型及观测模型。

图1 双天线GNSS/INS初始对准模型结构Fig.1 The block diagram of the two antennas GNSS/SINS integrated alignment system

1.1 系统模型

双天线GNSS/INS初始对准系统模型如图1所示，初始对准速度、姿态系统误差模型采用载体速度相关参数置零后的惯性导航水平通道误差模型[17]。IMU(inertial measurement unit)陀螺零偏不符合高斯白噪声特性，建模为一阶高斯-马尔可夫过程[17]。

(1)

式中，状态参数δx中包含速度改正数、漂移误差角ψ及硬件零偏误差ε；F为系统矩阵[17]；w为系统噪声。

1.2 观测模型

1.2.1 速度误差观测方程

静基座对准条件下，速度误差观测方程为

Δv=δv+ζv

(2)

式中，ζv为速度观测噪声，由于真实速度的期望为0，则观测值Δv即为INS计算的速度。

1.2.2 姿态误差观测方程

IMU与GNSS1、GNSS2位置关系如图2所示，三者在载体坐标系下保持位置关系不变，l1、l2为天线杆臂，l12=l2-l1。

(3)

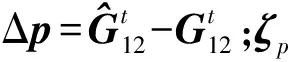
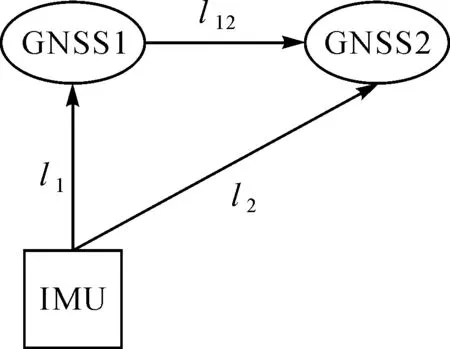
图2 载体坐标系下IMU及双天线结构Fig.2 Structure of two-antenna GNSS-SINS in body frame

综上，双天线GNSS/INS初始对准观测模型为

(4)

2 噪声协方差自适应控制下的卡尔曼滤波

Kalman滤波广泛应用于航空航天及目标跟踪等领域，是一种线性最小方差估计方法。相对于INS，GNSS自主性及抗差性较差，在实际应用中易受环境因素影响，如多路径、GNSS中断等。此时Kalman滤波解算精度依赖于系统模型的精度[19]。然而系统模型结构、状态参数及噪声统计信息存在未知部分，需优化Kalman滤波相关参数(如系统噪声协方差矩阵Q、观测噪声协方差矩阵R及误差协方差矩阵P)，以实现导航参数最优化解算。

P反映Kalman滤波初始状态误差水平，其影响局限在初始收敛过程中，对全局影响小，不作为参数优化重点，Q、R为参数优化的重点。Q表达状态参数的噪声强度，无法直接变换，采用衰退矩阵Γ控制P预测，并提出Γ获取方法；R反映观测值精度，需基于观测值质量对R进行调节。本节基于EKF说明噪声协方差预测优化方法。

2.1 EKF

EKF模型包含系统方程及观测方程两部分

(5)

EKF算法流程包括系统更新及测量更新。系统更新包括状态预测和误差协方差预测，如下

(6)

(7)

式中，I为单位矩阵。

2.2 系统噪声协方差优化

因无法直接控制Q[20]，可利用衰退因子fade放大协方差预测值，降低参数解算受系统模型误差的影响程度[21]。一步预测的协方差预测表达式为

Pfade(k|k-1)=fade(Pk|k-1)

(8)

速度、姿态及陀螺零偏为不同观测值，不应该采用同一衰退因子进行控制。则选择衰退矩阵Γ取代λ，即

Γ=diag[fadeV,fadeψ,fadeε]

(9)

式中

fadeV=diag[fadevNfadevE]

fadeψ=diag[fadeψNfadeψEfadeψD]

fadeε=diag[fadeεxfadeεy]

陀螺零偏为间接观测值，则fadeεx、fadeεy等于1[21]。令

(10)

式中，N为相关窗口[22]；vk和i0表达式如下

(11)

(12)

则λV、λε中对角线元素可利用式(13)计算，即

(13)

若fade′>1,说明系统模型不稳定；反之，系统模型稳定，Pk|k-1接近真实系统噪声特性[23]。

2.3 观测噪声协方差优化

Kalman滤波的噪声参数优化即寻求收敛速度与滤波稳定性之间的平衡，关键问题在于Kk的计算。若Pk|k-1/Rk偏小，Kk随之减小，状态参数回归真值的过程变慢；反之，Kk增大，状态参数解算更依赖观测值，扩大了观测噪声的影响，易导致滤波不稳定或产生估计偏差，观测噪声会通过系统模型对状态估计产生正反馈而导致滤波发散，状态参数远离真值[24]。在理想的Kalman滤波器中，对噪声模型进行调整并给出一致的估计误差与不确定度也能得到状态参数稳定估计[25]，考虑带宽限制下观测噪声时间相关性及同步误差，适当放大Rk是有必要的，一般要给比相应的标准差2到3倍的状态不确定度。令Rk表达形式如下

(14)

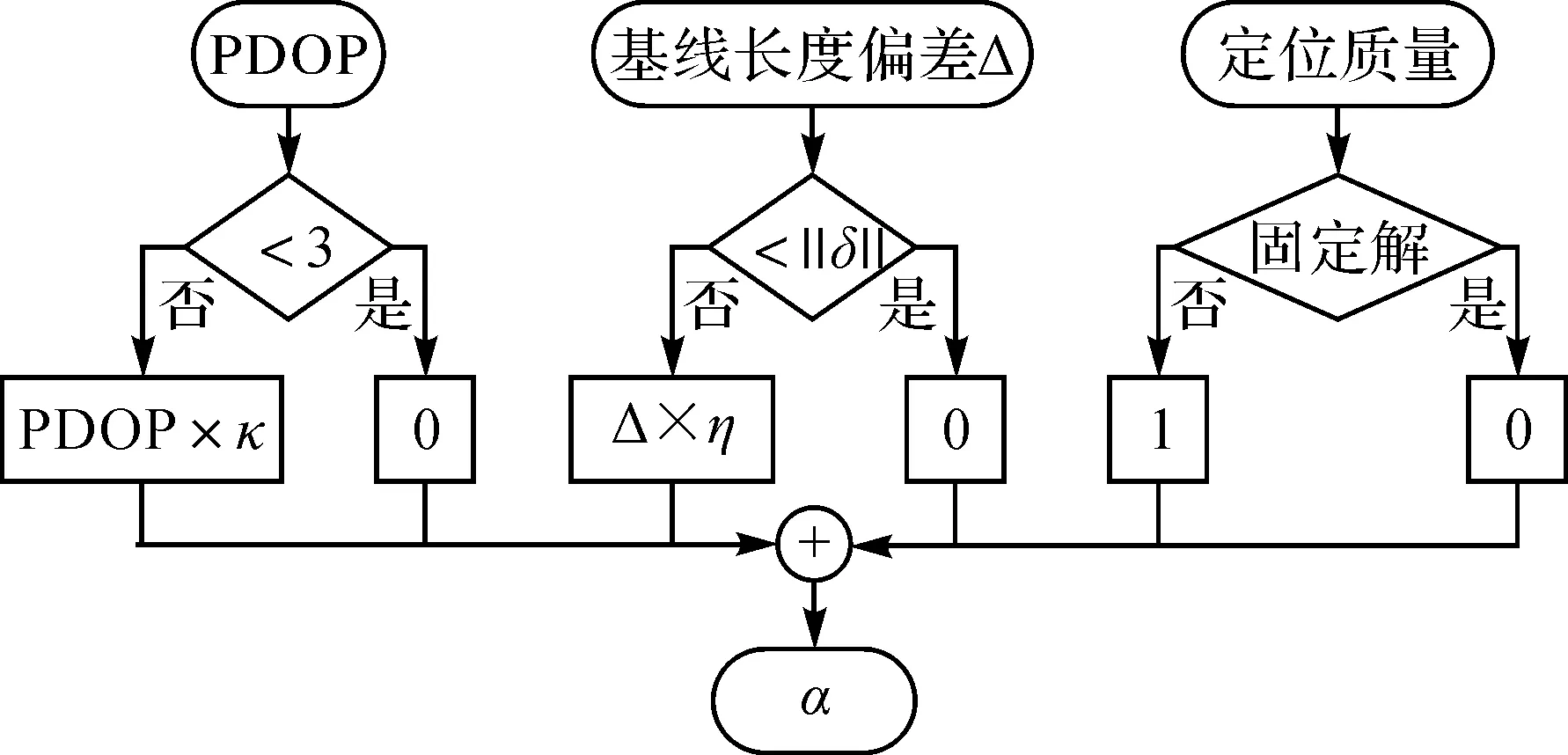
图3 GNSS数据质量模拟器Fig.3 Quality indicator of GNSS data

α的作用在于根据定位质量、PDOP值以及基线长度偏差调节Rk，在观测值精度较差时降低观测噪声的影响。κ、η用于量化观测数据质量，可取0.1～0.5，以保证Rk在适当的范围内调节。取值越大，对准模型的抗差性越强，但也会降低高精度观测值对姿态误差的补偿能力；取值越小，参数解算更依赖观测值精度，易放大观测噪声的影响。有关系统、观测噪声自适应机制对解算稳定性及精度的影响将在试验部分进行阐述。

3 试验分析

3.1 试验方案

为证明本文理论的可行性，设计4个方案，对比其速度、姿态参数协方差分布，利用国内成熟组合导航数据处理商用软件处理更高精度POS(position and orientation system)设备采集数据的对准结果，作为参考真值对比绝对精度，反映不同试验方案初始对准性能，参考POS设备对准结如表1。

表1 真实对准结果

(1) 方案1：基于EKF的双天线GNSS/INS初始对准。

(2) 方案2：基于系统噪声协方差自适应控制的双天线GNSS/INS初始对准。

(3) 方案3：基于系统、观测噪声协方差自适应控制下的双天线GNSS/INS初始对准。

(4) 方案4：基于方案3，加入天线间距约束条件下的双天线GNSS/INS初始对准。

4种方案均采用两精度等级POS 设备进行数据采集，IMU采样率均为200 Hz，GNSS采样率均为1 Hz，采样时间均为488 s，双天线间杆臂长度为0.70 m。为探究天线间基线矢量对姿态解算的辅助能力，采样环境开阔，可获取高精度天线间基线解。测试POS以及参考高精度POS相关技术指标如表2，其技术指标表明对应系统导航参数解算的稳定性，不代表绝对精度。

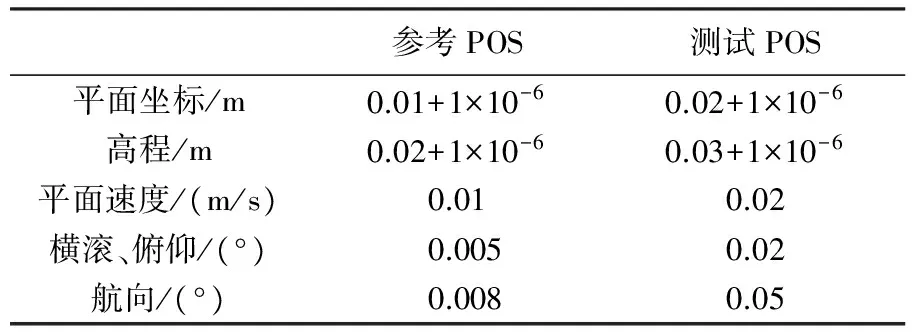
表2 相关技术指标

3.2 数据质量分析

根据图4，速度、姿态衰退因子二者均存在大于1的情况，表明Pk|k-1偏离真实的协方差预测值。为降低系统模型误差的影响，利用Γ放大Pk|k-1，以降低系统噪声对状态参数解算的影响。PDOP存在大于3的情况，认为此时卫星星座不利于位置解算，应适当放大观测噪声。

图4 衰退因子分布及PDOPFig.4 Distribution of fade factors and PDOP

图5为卫星定位质量，1代表固定解，0代表浮点解，对准过程中人为加入了时间为15 s、10 s、20 s及10 s的GNSS仿真中断，目的在于制造GNSS浮点解。

图5 定位质量Fig.5 Positioning quality

图6为基线长度偏差分布，一定程度上反映了对准模型中观测值的精度。基线解算后期存在较大的基线偏差，最大偏差可达0.021 cm。

对准过程中，出现系统预测异常及观测值精度较差时，利用Γ、α调节系统噪声与观测噪声对状态参数解算的干预程度，可降低以上模型误差对状态参数的影响。

3.3 试验结果分析

4种方案的对准误差如表3，滤波精度见图7。4种方案平面度滤波精度无明显差异，为

0.008 1 m/s；横滚角及俯仰角无明显差异，为0.006°；4种方案的航向角滤波精度分别为0.047°、0.022°、0.022°、0.020°。根据试验结果，可以得到如下结论：

(1) 相对于标准EKF，系统噪声协方差优化方法可提升对准滤波稳定性，降低收敛后稳态值，但未能提高所有姿态参数绝对精度，推测其原因为观测噪声模型不够精确。

(2) 加入观测噪声协方差优化机制，姿态角收敛速度稍微变慢，但滤波精度未受到影响。同时兼顾系统及观测噪声模型优化不仅维持了滤波稳定性，且能提高对准绝对精度，说明参数解算绝对精度同时受系统噪声统计信息及观测噪声统计信息影响，验证了结论(1)的推测。

(3) 基于方案3、方案4采用后处理的方式，利用基线长度偏差最小的基线结果辅助INS初始对准，对准绝对精度均有提升，航向角精度提升明显，可以认为对准后期，低质量GNSS基线结果影响了对准精度。说明参数解算绝对精度不仅受噪声统计信息影响，同时依赖于观测值精度。

图6 基线长度偏差分布Fig.6 Bias of baseline length distribution

(°)

图7 4种方案协方差分布Fig.7 Covariance distribution of four plans

4 结束语

本文讨论了一种基于噪声协方差自适应控制下的双天线GNSS/INS初始对准方法，该方法可降低系统模型误差及GNSS定向粗差等观测模型误差的影响，提升对准精度。试验结果表明，相对于标准EKF，系统噪声协方差自适应控制机制可提高系统的稳健性，提高对准的滤波精度，但受观测噪声影响，绝对精度没有明显提高；加入观测噪声自适应控制机制后，可以降低观测噪声对参数解算的影响，提高对准绝对精度；加入基线长度约束，对准绝对精度进一步提高，说明对准绝对精度受观测值精度影响较大，观测噪声模型优化及观测值质量控制是参数解算的关键。综上，利用本文方法，可提高GNSS/INS初始对准系统稳定性及对准绝对精度。

参考文献：

[1] 曹娟娟, 房建成, 盛蔚, 等. 低成本多传感器组合导航系统在小型无人机自主飞行中的研究与应用[J]. 航空学报, 2009, 30(10): 1923-1929.

CAO Juanjuan, FANG Jiancheng, SHENG Wei, et al. Study and Application of Low-cost Multi-sensor Integrated Navigation for Small UAV Autonomous Flight[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1923-1929.

[2] ZHANG Yufeng, GAO Yang. A Method to Improve the Alignment Performance for GPS-IMU System[J]. GPS Solutions, 2007, 11(2): 129-137.

[3] HONG S, CHANG Y S, HA S K, et al. Estimation of Alignment Errors in GPS/INS Integration[C]∥Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR: Oregon Convention Center, 2002: 24-27.

[4] 庞春雷, 赵修斌, 余永林, 等. 低精度SINS初始对准/GPS双天线测向互辅算法[J]. 西安电子科技大学学报, 2014, 41(6): 167-173.

PANG Chunlei, ZHAO Xiubin, YU Yonglin, et al. Interact Arithmetic of Low-accuracy SINS’ Initial Alignment and GPS Orientation Measurement with Two Antennas[J]. Journal of Xidian University, 2014, 41(6): 167-173.

[5] 何正斌. GPS/INS组合导航数据处理算法拓展研究[D]. 西安: 长安大学, 2012.

HE Zhengbin. Study on Algorithms Extension in GPS/INS Integrated Navigation[D]. Xi’an: Chang’an University, 2012.

[6] NARASIMHAPPA M, RANGABABU P, SABAT S L, et al. A Modified Sage-Husa Adaptive Kalman Filter for Denoising Fiber Optic Gyroscope Signal[C]∥Proceedings of 2012 Annual IEEE India Conference. Kochi, India: IEEE, 2012: 1266-1271.

[7] MOHAMED A H, SCHWARZ K P. Adaptive Kalman Filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73(4): 193-203.

[8] 杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293-298.

YANG Yuanxi, HE Haibo, XU Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 293-298.

[9] 杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版), 2003, 28(6): 714-718.

YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718.

[10] 张双成, 杨元喜, 张勤. 一种基于抗差自校正Kalman滤波的GPS导航算法[J]. 武汉大学学报(信息科学版), 2005, 30(10): 881-884.

ZHANG Shuangcheng, YANG Yuanxi, ZHANG Qin. An Algorithm of GPS Navigation Based on Robust Self-tuning Kalman Filtering[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 881-884.

[11] 杨元喜. 动态系统的抗差Kalman滤波[J]. 解放军测绘学院学报, 1997, 14(2): 79-84.

YANG Yuanxi. Robust Kalman Filter for Dynamic Systems[J]. Journal of the PLA Institute of Surveying and Mapping, 1997, 14(2): 79-84.

[12] 胡国荣, 欧吉坤. 改进的高动态GPS定位自适应卡尔曼滤波方法[J]. 测绘学报, 1999, 28(4): 290-294.

HU Guorong, OU Jikun. The Improved Method of Adaptive Kalman Filtering for GPS High Kinematic Positioning[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4): 290-294.

[13] 胡丛玮, 刘大杰. 基于方差分量估计原理的自适应卡尔曼滤波及其应用[J]. 测绘学院学报, 2002, 19(1): 15-18.

HU Congwei, LIU Dajie. Adaptive Kalman Filtering and Its Application Based on Variance Component Estimation[J]. Journal of Institute of Surveying and Mapping, 2002, 19(1): 15-18.

[14] YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353-358.

[15] YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components[J]. The Journal of Navigation, 2003, 56(2): 231-240.

[16] YANG Yuanxi, GAO Weiguang. A New Learning Statistic for Adaptive Filter Based on Predicted Residuals[J]. Progress in Natural Science, 2006, 16(8): 833-837.

[17] 高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.

GAO Zhongyu. Inertial Navigation System Technology[M]. Beijing: Tsinghua University Press, 2012.

[18] YANG Yunchun, FARRELL J A. Two Antennas GPS-aided INS for Attitude Determination[J]. IEEE Transactions on Control Systems Technology, 2003, 11(6): 905-918.

[19] GREWAL M S, ANDREWS A P, BARTONE C G. Global Navigation Satellite Systems, Inertial Navigation, and Integration[M]. 3rd ed. Hoboken, New Jersey: John Wiley & Sons, 2013.

[20] KIM J, LEE S. A Vehicular Positioning with GPS/IMU Using Adaptive Control of Filter Noise Covariance[J]. ICT Express, 2016, 2(1): 41-46.

[21] 甘雨, 隋立芬, 刘长建, 等. 自适应抗差Kalman滤波在多天线原始观测值瞬时姿态确定中的应用[J]. 测绘学报, 2015, 44(9): 945-951. DOI: 10.11947/j.AGCS.2015.20140492.

GAN Yu, SUI Lifen, LIU Changjian, et al. Instantaneous Attitude Determination Based on Original Multi-antenna Obser-vations Using Adaptively Robust Kalman Filtering[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 945-951. DOI: 10.11947/j.AGCS.2015.20140492.

[22] ROSS T J. Fuzzy Logic with Engineering Applications[M]. Hoboken, NJ: John Wiley & Sons, 2004.

[23] CHUI C K, CHEN Guanrong. Kalman Filtering with Real-time Applications[M]. Berlin: Springer, 1987.

[24] YANG Yuanxi, CUI Xianqiang. Adaptively Robust Filter with Multi Adaptive Factors[J]. Survey Review, 2008, 40(309): 260-270.

[25] GROVES P D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. Boston: Artech House, 2008.