联合EGM2008模型重力异常和GOCE观测数据构建超高阶地球重力场模型SGG-UGM-1

梁 伟，徐新禹,2，李建成,2，朱广彬

1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079； 3. 国家测绘地理信息局卫星测绘应用中心，北京 100048

构建超高阶地球重力场模型一直是物理大地测量学领域的热点研究问题。采用重力梯度测量技术的GOCE重力卫星于2009年成功发射，仅利用其观测数据恢复的全球重力场模型阶次达到了280阶[1]，模型中长波分量的精度更是有了2个数量级的提高，尤其在地面重力数据空白区，相比由GRACE和地面观测数据联合反演的EIGEN-5C等模型，在100 km空间分辨率上，GOCE任务反演的模型精度有了明显提升[2]。这一进展使得联合GOCE卫星观测数据和地面观测数据获得全球更高精度的超高阶重力场模型成为可能。反演的超高阶重力场模型可用于区域高精度大地水准面的确定[3]、全球高程基准的统一[4]、地球内部结构反演[5]等科学研究及应用。

基于球面重力异常数据反演超高阶全球重力场模型常用的方法主要有数值积分(numerical quadrature，NQ)方法、最小二乘配置(least squares collocation，LSC)方法和最小二乘(least squares，LS)方法[6]。NQ方法是基于面球谐函数的正交性，采用积分方法独立求解模型的每个系数，其计算简单，但无法直接给出模型系数的验后方差。相比NQ方法，LS方法不仅可评估模型系数的精度，而且可以联合解算多类观测数据。同时，在LS方法中，如果位系数按照特定的顺序排列，法方程矩阵会具有块对角特点，因此可以分块求解位系数，这种方法称为块对角最小二乘(block diagonal least squares，BDLS)方法[6]。该方法可避免超高维矩阵的构建及求逆，计算量大大减少，已成为目前求解超高阶重力场模型的主要方法，国际上精度得到认可的EGM96[7]、EGM2008[8]、EIGEN-6C4[9]等模型在构建时均使用了该方法。文献[10]分析了BDLS方法在重力场模型确定中的应用，并通过模拟试验比较了BDLS方法与NQ方法求解360阶重力场模型的精度。

考虑到卫星重力观测数据和重力异常数据在反演全球重力场模型时存在频谱互补性，前者对重力场的中长波信号更为敏感，后者对短波及甚短波信号更为敏感，因此联合卫星重力数据和重力异常数据可以反演得到高精度高分辨率的重力场模型，这也是当前求解超高阶重力场模型的主要方法。EGM2008模型构建时联合了GRACE卫星观测法方程和重力异常数据[8]，EIGEN-6C4模型不仅使用了这些数据，还使用了GOCE观测数据，相比EGM2008模型在一些区域的精度有明显提高[9]。文献[11]联合EGM2008模型和GOCE-TIM-R5模型解算了2160阶次重力场模型GECO；文献[12]采用全矩阵求逆的最小二乘方法解算了720阶次的GOCO05c模型，模型精度在15′的空间分辨率上(720阶次)与EIGEN-6C4相当；文献[13]基于卫星、陆地、海洋等观测数据，使用球谐分析方法确定了2159阶次的UGM08模型；文献[14]采用谱权组合方法联合EIGEN-6S卫星重力场模型和格网重力异常构建了2160阶次的重力场模型。

本文将研究BDLS方法的基本原理，并将OpenMP并行计算技术引入到BDLS方法的求解中，研制相应的软件模块，并基于数值模拟试验，分析BDLS方法求解2160阶重力场模型的精度及软件模块的可靠性。然后联合由GOCE任务独立建立的卫星观测法方程和EGM2008模型格网重力异常法方程，采用最小二乘方法估计一个2159阶次的重力场模型，并利用独立的GPS/水准数据对模型精度进行分析与检验。

1 基本原理

1.1 由重力异常数据快速求解模型系数的BDLS方法

格网平均重力异常观测值的观测方程为[6]

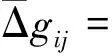
(1)

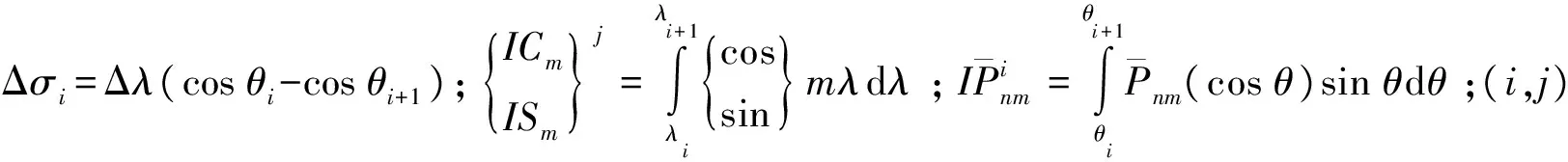
由式(1)，可以建立如下误差方程

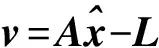
(2)

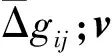
(3)

使用LS方法构建法方程时，当重力异常数据及其精度的空间分布满足下面4个条件时，法方程为稀疏矩阵，如按照一定顺序排列待求解参数，法方程矩阵N为块对角形式[16]：

(1) 格网数据分布于旋转曲面上(例如球面上)；

(2) 格网数据覆盖整个曲面且经度方向的分辨率一致；

(3) 格网数据的精度与经度无关，即数据的权重不依赖于经度的变化；

(4) 格网数据的精度关于赤道对称，即纬度θ与-θ处的数据精度相同。

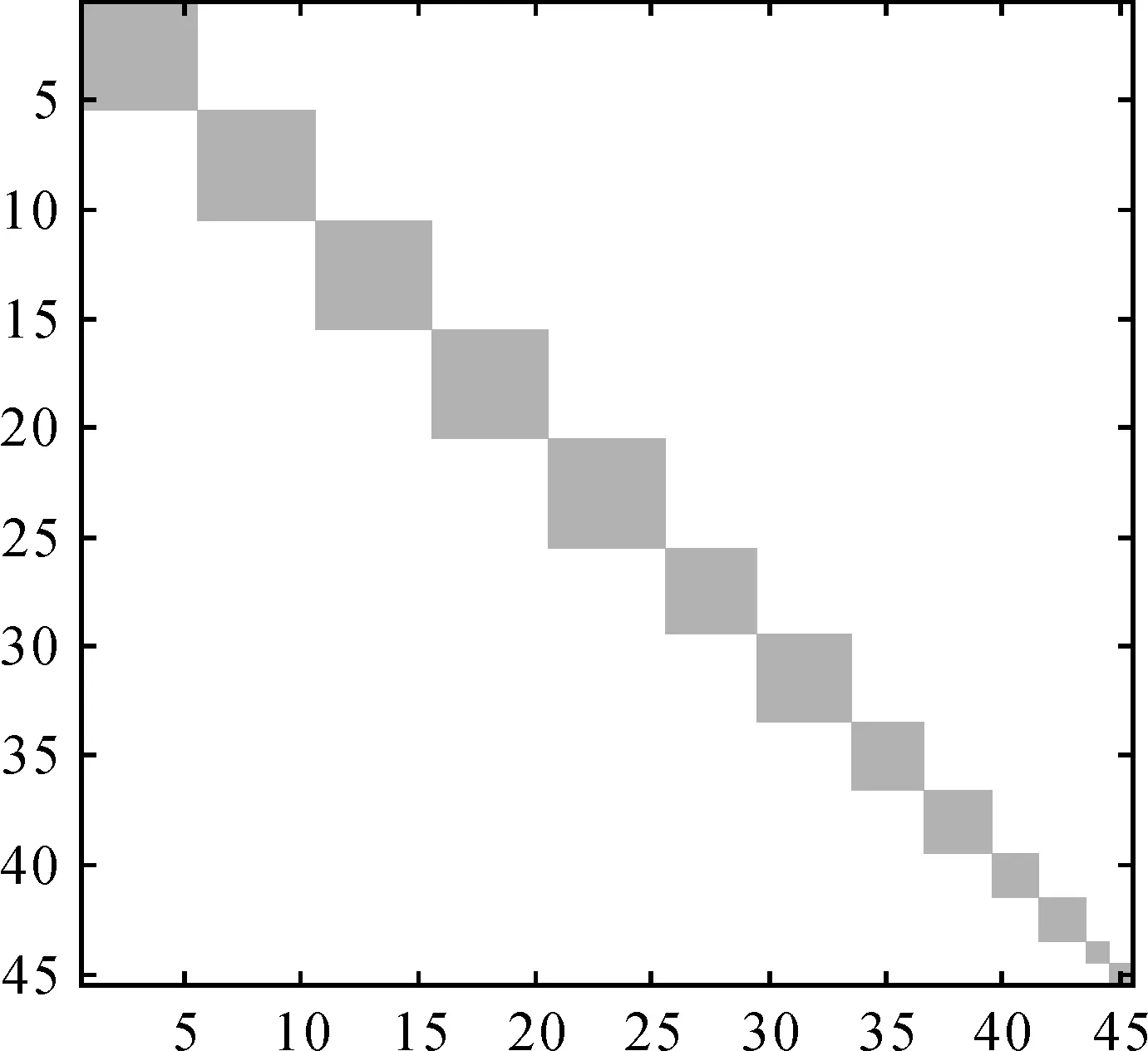
灰色部分代表非零元素，其余为零元素图1 法方程矩阵的结构示意图Fig.1 The schematic diagram of the normal matrix

如果法方程矩阵为块对角形式，求解参数时可以不构建和求解整个法方程，而是根据法方程具体的分块结构，单独构建法方程矩阵N中的每个块对角部分及与其对应的U，形成子法方程，对其单独求解，所有子法方程解的组合与原法方程的解完全一致。这种求解参数的方法称为块对角最小二乘(BDLS)方法。求解超高阶重力场模型时，参数个数较多，法方程庞大，现有的计算条件很难满足严格LS方法的计算需求，而BDLS方法可以避免大型矩阵的构建及求逆，计算量远小于LS方法。

值得注意的是，对于实际重力观测数据，可以对其进行处理使其满足条件(1)和(2)，但是处理后的数据的精度特点很难满足条件(3)和(4)，此时法方程不是严格块对角结构，而是块对角占优的结构。此时，如果仅取法方程的块对角部分采用BDLS方法会带来计算误差。文献[17]通过模拟试验探讨了重力异常数据精度的空间分布不满足条件(3)和(4)时BDLS方法的计算误差。结果表明，当全球重力异常数据精度的空间分布存在差异，且其差异达到10 mGal(1 mGal=10-5m/s2)的情况下，采用BDLS方法仍能以较高的精度求解重力场模型，因此本文将不考虑重力异常数据精度的空间差异性问题。

1.2 多源重力观测数据的最小二乘联合求解

本文联合重力异常数据和GOCE卫星重力数据的方法是最小二乘联合平差方法[18-19]，它的基本原理如下：

可以分别根据观测数据L1和L2的观测模型建立它们的误差方程如式(4)所示

(4)

在最小二乘准则下可以建立数据L1和L2的法方程如式(5)所示，求解法方程可以得到待求参数

(5)

式中，P1、P2分别为数据L1和L2的权阵。

同时也可联合数据L1和L2，建立它们联合观测的误差方程如下

(6)

式中，vC=[v1v2]T；AC=[A1A2]T；lC=[l1l2]T。

在最小二乘准则下可以建立它们的联合观测法方程，如式(7)所示

(7)

式中，PC为数据的权阵。

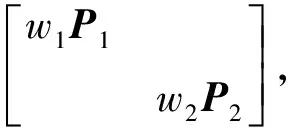
(8)

由式(8)可知，当数据L1和L2不相关时，使用最小二乘联合平差方法联合数据L1和L2构建的法方程和直接将各类观测数据构建的法方程按照加权因子相加形成的法方程相同[18-19]。即当观测数据不相关时，直接把法方程加权相加就可实现多源数据的最小二乘联合处理，这种方法简单有效。

在最小二乘联合平差中的一种特殊情况是数据L1和L2求解的参数x1和x2可能不完全一样，它们构建的法方程的参数和维数不同，这样不能直接将法方程相加。此时可以分别由数据L1和L2构建参数x1和x2的参数集合xC的误差方程。此时建立的参数xC的误差方程与原来参数x1和x2的误差方程的区别在于设计矩阵中增加了0元素，这些0元素是与观测量无关的参数的系数。进而建立参数xC的法方程，此时将法方程相加可以得到它们对参数xC的联合观测法方程。

2 基于OpenMP技术的块对角最小二乘软件模块设计及验证

构建超高阶重力场模型需要求解的参数较多，虽然BDLS方法的计算量远小于LS方法，但是一般计算机在单核单进程下使用BDLS方法求解2160阶重力场模型的时耗仍很长。为提高BDLS方法的计算效率，本文将OpenMP并行计算引入BDLS方法的解算中，在高性能计算平台上实现超高阶重力场模型的快速解算。

并行计算是指同时使用多种计算资源完成计算任务，是缩短计算时间的有效手段。常用的并行计算有OpenMP多线程技术和MPI多进程技术。OpenMP可为程序中的并行计算区域开辟多个线程，每个线程独立运行，多个线程协同完成并行计算区域的计算任务[20-21]。

使用BDLS方法求解超高阶重力场模型时，需要依次构建法方程矩阵N中的块对角部分和U中与其对应的部分，并对其单独求解。法方程的每个块对角部分的构建和求解可单独进行，在程序设计时一般用DO循环完成。OpenMP技术可以为相互独立的DO循环开辟多个线程，将多个循环分配到多个线程上运行，充分利用高性能计算平台的计算资源，以提高计算效率。

根据BDLS方法和OpenMP技术的特点，本文设计了求解超高阶重力场模型的OpenMP并行计算软件模块。为验证BDLS方法和编写软件模块的正确性，设计了以下模拟试验：使用EGM2008模型(截断到2159阶)模拟计算了半径为6 378 136.3 m球面上分辨率为5′×5′的格网重力异常平均值数据，基于该数据使用编写的BDLS并行计算软件模块求解了2159阶的重力场模型，命名为TestModel，它的系数阶误差RMS如图2所示(见后文)。试验使用的计算机为HP服务器，所用计算节点上有20个主频为2.4 GHz的Intel Xeon CPU，在单节点上运行，使用了80个线程，计算耗时7 h。从图2可以看出，求解的模型系数的误差小于10-11量级，试验结果验证了BDLS方法和相应软件模块的正确性，可以高效精确地求解超高阶重力场模型。

3 SGG-UGM-1超高阶重力场模型的求解

EGM2008重力场模型在构建时使用了精度较高且覆盖较全的地面重力数据集[8]，本文使用其计算球面上的全球重力异常格网平均值，并联合该数据和GOCE卫星数据解算了2159阶次重力场模型SGG-UGM-1。

3.1 超高阶重力场模型解算的数据处理流程

本文构建超高阶重力场模型的解算流程如图3 所示，具体描述如下：

(1) 使用EGM2008模型计算参考球面(球半径为6 378 136.3 m)上5′×5′格网分辨率的重力异常数据ΔgEGM；由该数据使用BDLS方法构建并求解2159阶块对角法方程，得到2～2159阶位系数，这部分系数命名为BDLS，使用BDLS方法构建法方程时认为格网数据的权相等。

(2) 根据步骤(1)求得系数中2～100阶以及251～2159阶系数计算重力异常，然后在数据ΔgEGM中减去这部分重力异常得到残余重力异常数据ΔgR。ΔgR数据中仅有101～250阶系数的贡献，再使用ΔgR数据构建101～250阶系数的块对角法方程。

(3) 使用GOCE卫星的卫星重力梯度(satellite gravity gradiometry，SGG)数据和卫星跟踪卫星(satellite-to-satellite tracking，SST)数据构建220阶卫星观测法方程，并求解得到220阶的卫星重力场模型，其数据处理方法的描述见下节。

(4) 步骤(2)建立了101～250阶系数的法方程，步骤(3)建立了2～220阶系数的法方程，使用1.2节描述的联合平差方法，联合这两个法方程得到2～250阶系数的联合观测法方程。3.3节中有关于法方程联合过程更为详细的描述。

(5) 求解步骤(4)建立的2～250阶系数联合观测法方程，可以得到2～250阶系数，这部分系数与步骤(1)中求解的系数中251～2159阶部分一同组成2～2159阶重力场模型系数。

3.2 GOCE 卫星观测法方程的构建

本文使用的GOCE卫星重力观测数据为2009年11月1日—2012年5月31日期间的SGG数据和2009年11月1日—2010年7月5日期间的SST数据，数据的采样间隔为1 s。其中包括：卫星重力梯度观测数据、梯度仪坐标系相对于惯性系之间的姿态数据(四元素)、精密卫星轨道数据、地固系与惯性系之间的转换矩阵、加速度观测数据、运动学轨道的方差-协方差数据等[18]。

基于上面的观测数据，建立GOCE卫星观测法方程的简要描述如下：首先，对原始数据进行粗差探测与剔除、时变重力场信号的分离、数据内插分段等预处理；直接利用沿轨的引力梯度对角线数据(Vxx，Vyy，Vzz)建立观测方程及相应的法方程，再使用方差分量估计方法估计引力梯度张量对角线分量各自的单位权中误差，3个分量的单位权中误差分别为2.5、3.3和4.3 mE。考虑到引力梯度观测值的有色噪声特点，在最小二乘过程中引入通带为0.005～0.041 Hz的ARMA(auto regressive moving-average)滤波器。采用点域加速度方法由PKI(precise kinematic orbit)轨道观测值建立相应的SST法方程，求解SST法方程得到观测值残差，并基于残差估计了单位权方差。基于SGG各分量的单位权方差以及SST的单位权方差，得到了它们之间的加权因子，最后基于加权因子将SGG数据各分量的法方程以及SST法方程相加得到GOCE卫星观测法方程，并求解得到相应的卫星重力场模型，求解时采用Tikhonov正则化方法解决极空白问题引起的法方程不稳定性问题。文献[18]中有更为详细的数据处理方法和过程的描述。

图3 SGG-UGM-1模型的解算流程Fig.3 Calculation process of SGG-UGM-1 model

3.3 GOCE 卫星观测法方程和格网重力异常法方程的联合解算

联合求解GOCE卫星法方程与重力异常块对角法方程可以得到最优的模型解，但是由于两个法方程在形式、阶次、频谱精度上有较大差异，联合解算时需要采取有效的策略。根据文献[9]，本文制定的法方程联合解算策略如图4所示。

使用EGM2008模型的系数误差信息，可以计算得到模型在2190阶的重力异常累计误差约为5 mGal。本文使用5 mGal作为重力异常数据的单位权中误差，并基于该单位中误差以及上文中GOCE 数据的单位权方差得到重力异常法方程与GOCE观测法方程的加权因子。

联合观测法方程分为两部分，其中251～2159阶系数法方程与重力异常法方程中对应部分相同，而2～250阶系数法方程是使用1.2节中的最小二乘联合平差方法联合101～250阶重力异常数据块对角法方程和GOCE全阶次法方程(220阶)得到的。构建重力异常数据101～250阶块对角法方程时需要在原始重力异常数据中移除2～100阶及251～2159阶系数的贡献。

模型的220～250阶系数是联合GOCE数据和重力异常数据联合求解的，这样可以保证联合模型的这部分系数及其验后方差的频谱有更好的连续性。重力异常数据求解低阶系数的精度较差，重力异常低阶次系数法方程与卫星法方程联合可能会“污染”卫星重力的低阶系数，所以为减弱其影响，2～250阶联合法方程中只采用了重力异常的101～250阶系数块对角法方程。

4 SGG-UGM-1超高阶重力场模型的精度分析

4.1 SGG-UGM-1模型的系数误差

EIGEN-6C4模型是当前精度较高的超高阶重力场模型[11]。本文以此为参考模型，认为该模型的系数为“真值”计算SGG-UGM-1、GOSG-EGM、EGM2008和EIGEN-6C2[22]模型的“误差”，并对它们的误差进行对比分析，以在频域内分析SGG-UGM-1的特性，评价模型的精度与合理性。

GOSG-EGM模型是利用本文计算得到的220阶卫星重力场模型与EGM2008重力场模型系数直接拼接得到的，其2～220阶系数来自卫星重力场模型，221～2159阶系数来自EGM2008模型。图5给出了SGG-UGM-1、GOSG-EGM、EGM2008和EIGEN-6C2模型系数的阶误差RMS。

由图5可知，在2～70阶的频率范围内，EIGEN-6C2的误差最小，EGM2008次之，而SGG-UGM-1和GOSG-EGM较大。这是由于EIGEN-6C2与EIGEN-6C4的2～70阶系数的计算方法和使用数据类似，都是联合LAGEOS、GRACE和GOCE 等数据求解的[9,22]，EGM2008的2～70阶次系数主要是来自于GRACE观测数据的贡献；而SGG-UGM-1和GOSG-EGM的2～70阶次系数主要由GOCE 数据求解，因此其与EIGEN-6C4模型的差异大于EGM2008、EIGEN-6C2。

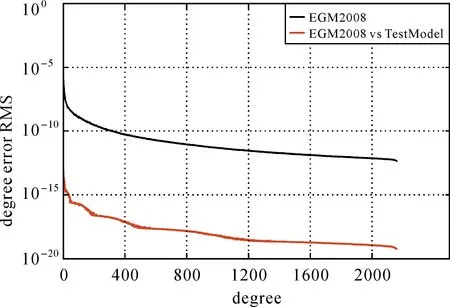
图2 模型的系数阶误差RMSFig.2 Degree error RMS of the model coefficients

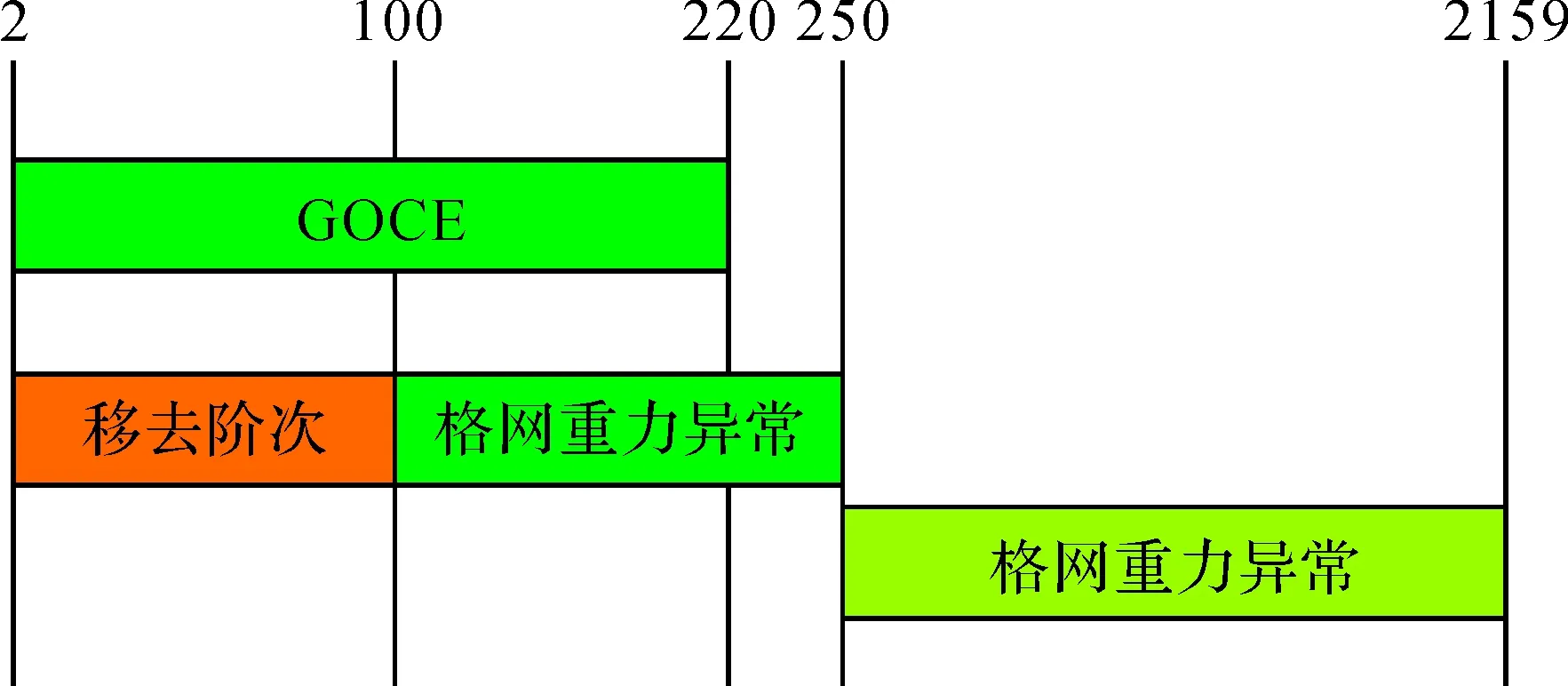
图4 SGG-UGM-1的法方程联合解算示意图Fig.4 The schematic diagram of normal equation combination in SGG-UGM-1

图5 重力场模型的系数阶误差RMSFig.5 Degree error RMS of the gravity field models

在70～220阶，SGG-UGM-1和EIGEN-6C2与EIGEN-6C4更为接近，主要原因是两个模型在此频段内均有GOCE和地面重力数据的贡献，而GOSG-EGM仅有GOCE卫星的贡献，从170阶开始它的误差迅速增大。同时，在170～220阶部分，因为SGG-UGM-1是联合GOCE和地面重力数据解算的，因此比GOSG-EGM模型的系数误差平滑，在220阶没有出现突变现象。

图6为SGG-UGM-1等重力场模型的大地水准面阶误差，反映了系数的误差。图6中模型的大地水准面系数误差与系数相对参考模型的系数误差呈现出了一定的相似性。由图6可知，SGG-UGM-1的系数误差在220阶附近达到最大，然后开始下降，它的误差谱连续，没有出现突变现象。相比EGM2008、GOCE-EGM、BDLS模型，SGG-UGM-1模型低阶次的系数误差得到了明显改善，这也说明了本文模型联合求解方法的合理性。

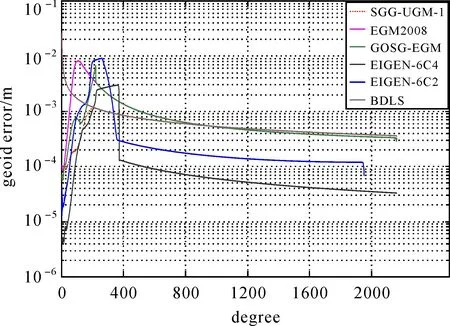
图6 重力场模型的大地水准面阶误差Fig.6 Degree geoid error of the gravity field models

频谱域的分析结果说明，本文求解的SGG-UGM-1模型精度可靠，且相比EGM2008模型在220阶次内的系数精度有了明显改善。

4.2 中国和美国GPS/水准数据的检核结果

为了分析SGG-UGM-1模型的外符合精度，本文使用中国区域的649个GPS/水准点数据[23]和美国区域的6169个GPS/水准点数据[24]对模型进行外部检核，并与GOSG-EGM、EGM2008、EIGEN-6C2及EIGEN-6C4模型的检核结果进行对比分析，结果见表1、表2。

表1中国区域的GPS/水准数据检核结果

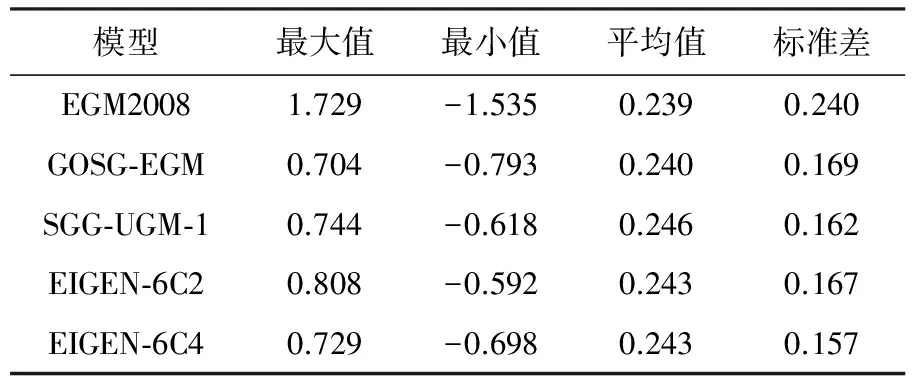
Tab.1 Validation of the gravity field models using GPS-leveling data in China m

表2美国区域的GPS/水准数据检核结果

Tab.2 Validation of the gravity field models using GPS-leveling data in America m

如表1所示，在中国区域SGG-UGM-1大地水准面的精度远优于EGM2008，略优于EIGEN-6C2和GOSG-EGM模型，略逊于EIGEN-6C4模型。如表2所示，在美国区域SGG-UGM-1模型的精度最高，但其他几个模型的精度基本相当。SGG-UGM-1模型在美国和中国区域的精度均优于EGM2008模型，这主要是因为SGG-UGM-1模型使用了GOCE数据，GOCE数据提高了模型低阶次系数的精度，这与上文的模型系数分析的结果一致。尤其与EGM2008模型在地面重力数据空白或稀疏区对比，SGG-UGM-1模型在这些区域(如中国大陆)的精度提升更为明显[25]。SGG-UGM-1模型的大地水准面在中国区域和美国区域的精度检核结果均优于GOSG-EGM，充分体现了最小二乘联合平差方法的优势。

4.3 毛乌素测区航空重力数据的检核结果

为了进一步分析SGG-UGM-1模型的外符合精度，本文使用毛乌素测区的航空重力扰动观测数据对模型进行外部检核，并与GOSG-EGM、EGM2008、EIGEN-6C2及EIGEN-6C4模型的检核结果进行对比分析，结果如表3示。毛乌素测区位于陕北地区，测区范围为38°48′N—39°16′N、109°17′E—110°27′E，测区大小为50 km×100 km。

表3航空重力数据的检核结果

如表3所示，在毛乌素测区，SGG-UGM-1模型计算重力扰动的精度略逊于EGM2008和EIGEN-6C4模型，优于GOSG-EGM和EIGEN-6C2模型，总体来说几个模型的精度相当。相比GPS水准检核的结果，虽然SGG-UGM-1模型的低阶次系数相较EGM2008模型有了较大提升，但由于其高阶次系数主要是由EGM2008模型重力异常求解的，且重力扰动的误差主要来自高阶次系数，所以SGG-UGM-1航空重力扰动的精度相较EGM2008没有提升。

5 总 结

本文使用EGM2008模型的5′×5′格网重力异常构建了2159阶次的块对角法方程，并使用最小二乘方法联合GOCE重力卫星任务220阶次的全阶次法方程求解了2159阶次的重力场模型SGG-UGM-1，使用EIGEN-6C4等重力场模型、中国与美国的GPS水准/数据和毛乌素测区的航空重力数据分析了SGG-UGM-1模型的内外符合精度。主要的结论如下：

(1) BDLS方法可以快速精确地确定超高阶重力场模型，采用OpenMP技术可以大幅度提高BDLS软件模块的计算效率。

(2) 采用最小二乘联合平差方法不仅可以保证求解模型在联合频段内信号和误差频谱的连续性，同时求解的模型SGG-UGM-1精度优于直接拼接获得的GOSG-EGM模型。

(3) 本文使用的GPS/水准数据对模型的检核结果表明，SGG-UGM-1大地水准面在中国区域的精度介于EIGEN-6C2和EIGEN-6C4两个模型之间，优于GOSG-EGM模型，远优于EGM2008模型；在美国区域这些模型的精度相当。

(4) 本文使用的毛乌素测区航空重力数据对模型的检核结果表明，SGG-UGM-1模型计算的重力扰动精度与EGM2008、EIGEN-6C4模型相当，优于GOSG-EGM模型和EIGEN-6C2模型。

模型的检核结果说明本文构建超高阶重力场模型策略的合理性，为进一步研究超高阶重力场模型的构建奠定了基础。但在联合卫星观测数据和重力异常数据时，本文参考了EIGEN-6C系列模型构建的经验，后续应该进一步深入研究重力异常法方程与卫星观测法方程的最优联合问题。SGG-UGM-1模型的低阶次系数的精度较EGM2008有了较大提升，但由于本文使用的重力异常数据是由EGM2008模型计算得到的，所以模型在高频段没有提升，且与EGM2008模型有很强的相关性。更为合理的做法是从全球高精度的地面重力、航空重力、卫星测高、地形等观测数据出发，完全独立自主处理各类数据得到全球高分辨率的重力异常格网数据集，然后据此反演超高阶重力场模型，这也是笔者后续的研究重点。

参考文献：

[1] BROCKMANN J M, ZEHENTNER N, HÖCK E, et al. EGM_TIM_RL05: An Independent Geoid with Centimeter Accuracy Purely Based on the GOCE Mission[J]. Geophysical Research Letters, 2014, 41(22): 8089-8099.

[2] PAIL R, GOIGINGER H, SCHUH W D, et al. Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE[J]. Geophysical Research Letters, 2010, 37(20): L20314.

[3] FEATHERSTONE W E. GNSS-based Heighting in Australia: Current, Emerging and Future Issues[J]. Journal of Spatial Science, 2008, 53(2): 115-133.

[4] RUMMEL R. Height Unification Using GOCE[J]. Journal of Geodetic Science, 2012, 2(4): 355-362.

[5] MCKENZIE D, YI Weiyong, RUMMEL R. Estimates ofTefrom GOCE Data[J]. Earth and Planetary Science Letters, 2014, 399(2): 116-127.

[6] PAVLIS N K. Modeling and Estimation of a Low Degree Geopotential Model from Terrestrial Gravity Data[R]. Report No.386. Columbus: The Ohio State University, 1988.

[7] LEMONIE F G, KENYON S C, FACTOR J K, et al. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96[R]. Greenbelt: NASA Goddard Space Flight Center, 1998.

[8] PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research, 2012, 117(3): 205-213.

[9] FÖRSTE C, BRUINSMA S L, ABRIKOSOV O, et al. EIGEN-6C4 the Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse[EB/OL]. http:∥doi.org/10.5880/icgem.2015.1.

[10] 李新星, 吴晓平, 李姗姗, 等. 块对角最小二乘方法在确定全球重力场模型中的应用[J]. 测绘学报, 2014, 43(8): 778-785. DOI:10.13485/j.cnki.11-2089.2014.0110.

LI Xinxing, WU Xiaoping, LI Shanshan, et al. The Application of Block-diagonal Least-squares Methods in Geopotential Model Determination[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 778-785. DOI:10.13485/j.cnki.11-2089.2014.0110.

[11] GILARDONI M, REGUZZONI M, SAMPIETRO D. GECO: A Global Gravity Model by Locally Combining GOCE Data and EGM2008[J]. Studia Geophysica et Geodaetica, 2016, 60(2): 228-247.

[12] FECHER T, PAIL R, GRUBER T, et al. GOCO05c: A New Combined Gravity Field Model Based on Full Normal Equations and Regionally Varying Weighting[J]. Surveys in Geophysics, 2017, 38(3): 571-590.

[13] 王正涛, 党亚民, 晁定波. 超高阶地球重力位模型确定的理论与方法[M]. 北京: 测绘出版社, 2011.

WANG Zhengtao, DANG Yamin, CHAO Dingbo. Theory and Methodology of Ultra-high-degree Geopotential Model Determination[M]. Beijing: Surveying and Mapping Press, 2011.

[14] 李新星. 超高阶地球重力场模型的构建[D]. 郑州: 信息工程大学, 2013.

LI Xinxing. Building of an Ultra-high-degree Geopotential Model[D]. Zhengzhou: Information Engineering University,

2013.

[15] 海斯卡涅W A, 莫里兹H. 物理大地测量学[M]. 卢福康, 胡国理, 译. 北京: 测绘出版社, 1979.

HEISKANEN W A, MORITZ H. Physical Geodesy[M]. LU Fukang, HU Guoli, trans. Beijing: Surveying and Mapping Press, 1979.

[16] COLOMBO O L. Numerical Methods for Harmonic Analysis on the Sphere[R]. Columbus: The Ohio State University,

1981.

[17] LIANG Wei, LI Jiancheng, XU Xinyu, et al. Analysis of the Impact on the Gravity Field Determination from the Data with the Ununiform Noise Distribution Using Block-diagonal Least Squares Method[J]. Geodesy and Geodynamics, 2016, 7(3): 194-201.

[18] XU Xinyu, ZHAO Yongqi, REUBELT T, et al. A GOCE Only Gravity Model GOSG01S and the Validation of GOCE Related Satellite Gravity Models[J]. Geodesy and Geodynamics, 2017, 8(4): 260-272.

[19] 钟波, 宁津生, 罗志才, 等. 联合GOCE卫星轨道和重力梯度数据严密求解重力场的模拟研究[J]. 武汉大学学报(信息科学版), 2012, 37(10): 1215-1220.

ZHONG Bo, NING Jinsheng, LUO Zhicai, et al. Simulation Study of Rigorous Gravity Field Recovery by Combining GOCE Satellite Orbit and Gravity Gradient Data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1215-1220.

[20] 陈国良. 并行计算: 结构·算法·编程[M]. 3版. 北京: 高等教育出版社, 2011.

CHEN Guoliang. Parallel Computing: Architecture, Algorithm and Programming[M]. 3rd ed. Beijing: Higher Education Press, 2011.

[21] 邹贤才, 李建成, 汪海洪, 等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报, 2010, 39(6): 636-641.

ZOU Xiancai, LI Jiancheng, WANG Haihong, et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 636-641.

[22] FÖERSTE C, BRUINSMA S L, FLECHTNER F, et al. A Preliminary Update of the Direct Approach GOCE Processing and a New Release of EIGEN-6C[C]∥Proceedings of American Geophysical Union 2012 Fall Meeting. San Francisco, USA: American Geophysical Union, 2012.

[23] LI Jiancheng, JIANG Weiping, ZOU Xiancai, et al. Evaluation of Recent GRACE and GOCE Satellite Gravity Models and Combined Models Using GPS/leveling and Gravity Data in China[M]∥MARTI U. Gravity, Geoid and Height Systems. Cham, Switzerland: Springer, 2014: 67-74.

[24] MILBERT D G. Documentation for the GPS Benchmark Data Set of 23-July-98[R]. Milan: IGeS International Geoid Service, 1998: 29-42.

[25] RUMMEL R, YI Weiyong, STUMMER C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777-790.