动态EIV模型及其总体卡尔曼滤波方法
余 航,王 坚,王乐洋,宁一鹏,刘志平
1. 中国矿业大学环境与测绘学院,江苏 徐州 221116; 2. 北京建筑大学测绘与城市空间信息学院,北京100044; 3. 东华理工大学测绘工程学院,江西 南昌 330013
卡尔曼滤波(Kalman filter,KF)方法已在组合导航、GPS定位及目标跟踪等方面取得了广泛应用,是一种处理动态模型获得时变参数的经典方法[1]。常用的卡尔曼滤波方法是基于最小二乘估计或最小方差估计的标准卡尔曼滤波方法[2]。此后,多种扩展方法相继提出,如抗差卡尔曼滤波、抗差自适应卡尔曼滤波、约束卡尔曼滤波,又如扩展卡尔曼滤波、无迹卡尔曼滤波、粒子滤波等[3]。然而,在某些导航应用中,动态模型中观测方程的系数矩阵及状态方程的状态转移矩阵均存在误差影响,严格意义上应考虑采用总体最小二乘(total least squares,TLS)平差方法。对于非动态系统,文献[4—6]首次将总体最小二乘方法的思想应用于求解大地测量领域中的坐标转换问题,此后许多学者对其进行了广泛研究[7-17]。对于动态系统,文献[18]同时顾及了动态系统的输入与输出项误差,将总体最小二乘方法转化为无约束非线性规划问题并用于航迹的微分平滑系统。由于绝大多数动态模型均呈现出非线性的特点,但变量间的非线性关系往往可通过线性化、变量变换等转化为线性关系,因此分析线性情况下的动态模型最为普遍。文献[19]在线性动态系统的条件下,首次提出的动态EIV(errors-in-variables,EIV)模型的概念,提出将总体最小二乘方法应用于求解动态EIV模型并谓之总体卡尔曼滤波(total Kalman filter,TKF)方法,但在推导过程中仅视观测方程的系数矩阵存在误差,且系数矩阵误差的方差-协方差阵须满足特定的结构,当观测方程存在粗差时,文献[20]将粗差探测方法应用于TKF方法中。文献[21]在文献[19]的基础上,去除了系数矩阵误差的方差-协方差阵的结构限制,给出了更为一般方差阵情况下的WTKF(weighted total Kalman filter,WTKF)方法。
本文在已有总体卡尔曼滤波方法的基础上,同时考虑了状态转移矩阵误差与系数矩阵误差的影响,给出了更为一般情况下的动态EIV模型。针对该模型的平差计算,采用虚拟观测法分别构建了预测部分与修正部分的TLS平差准则[22],推导了相应的总体卡尔曼滤波方法。以室内定位为背景,利用超宽带(ultra-wideband,UWB)提供的测距信息与惯性导航系统(inertial navigation system,INS)输出的角度信息和比力信息进行联合处理[23-25],将本文方法应用于确定室内载体的位置与姿态。算例结果表明了本文方法的有效性与可行性。
1 动态EIV模型及其总体卡尔曼滤波方法
1.1 动态EIV数学模型形式
在某一历元k,动态EIV模型的函数模型形式为
ξk=(φk-Eφk)ξk-1+fk+wk
(1)
yk=(Ak-EAk)ξk+Zk+eyk
(2)
式中,ξk为m×1维时变随机状态向量;φk为m×m状态转移矩阵;Eφk为φk的随机误差矩阵;yk为n×1维观测向量;Ak为n×m系数矩阵,其对应的随机误差矩阵为EAk;fk和Zk分别为状态方程和观测方程的控制向量;wk和eyk分别为m×1维随机系统噪声和n×1维观测噪声。
(3)
假设式(1)—式(3)中所有误差项在任意历元均互不相关,则动态EIV模型的随机模型为
(4)

(5)
(6)
1.2 动态EIV模型的总体卡尔曼滤波方法
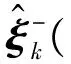
预测阶段,先对式(1)变换如下[14]
(7)
考虑矩阵运算
vec(ABC)=(CT⊗A)·vec(B)
(8)
式中,⊗表示Kronecker积。

(9)
(10)
(11)
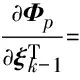
(12)
由式(11)可得如下等式成立
(13)
由式(12)可得
(14)
(15)
式中,ξk-1=[(ξk-1)1… (ξk-1)i… (ξk-1)m]T,i∈[1,m]。
式(15)中[8,14]
(16)

(17)
式中,Qφk=[(Qφk)1… (Qφk)i… (Qφk)m];(Qφk)i为Qφk中的第i个mm×m子矩阵。
因此,式(15)可推导得
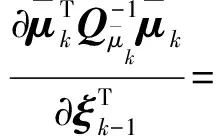
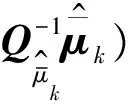
(18)
将式(14)和式(18)代入式(12),得到式(12)的具体表达式为

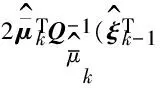
(19)
式(19)等价于
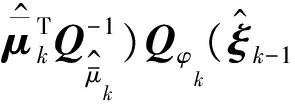
(20)


(21)
将式(21)代入式(20)得
(22)
上式等价于
(23)
结合式(13)与式(23)推导得
(24)
因此,一步预测值为
(25)
由式(1)、式(3)及式(25),计算一步预测残差

(26)

(27)
进而有


(28)
对式(28)采用协方差传播率,可得一步预测的方差-协方差阵为

(29)
式(25)与式(29)为修正计算提供了验前信息。在进行修正部分之前,同理对式(2)变换
(30)
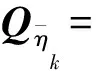


(31)
(32)
(33)
与预测部分的计算思路类似,可推导得到

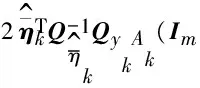

(34)
式(34)等价于

(35)


(36)
联立式(30)和式(36)得法方程如下
(37)
结合矩阵反演公式(V+CZD)-1=V-1-V-1C(Z-1+DV-1C)-1DV-1,并计算上述法方程得
(38)
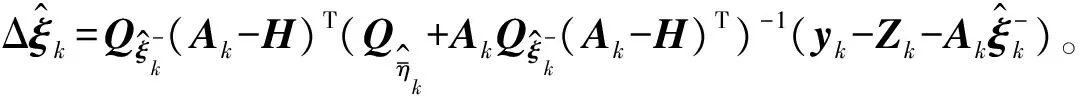
将式(38)的计算结果分别代入式(28)和式(30),得
(39)
(40)
采用条件平差法[14]得到相应误差改正项为

(41)
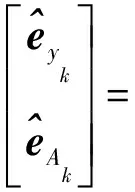
(42)

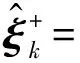
(43)

(44)
对式(44)采用协方差传播率可得验后状态估值的方差-协方差阵为
(45)
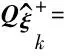
(46)
1.3 动态EIV模型总体卡尔曼滤波方法的迭代计算过程
动态EIV模型总体卡尔曼滤波方法的迭代计算过程如下:
(2) 历元k=k+1:输入观测数据φk、fk、Ak、yk、Zk、Qφk、θk和Qk。
(5) 计算:
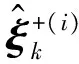
(8) 若k≤t(t表示总的历元数),重复步骤1-7,否则,迭代结束。
2 算例与分析
仿真试验:模拟室内轨迹(如图1所示),载体利用UWB给出的距离观测值与INS提供的角度及比力信息进行位置和载体姿态的确定。为了计算方便,设初始时刻载体系(xt,yt,zt)与导航系(xn,yn,zn)严格对齐(即初始姿态角为零),导航系采用东北天坐标系;为了计算方便,文中将轨迹及UWB基站的坐标均融入自定义的局部坐标系中。
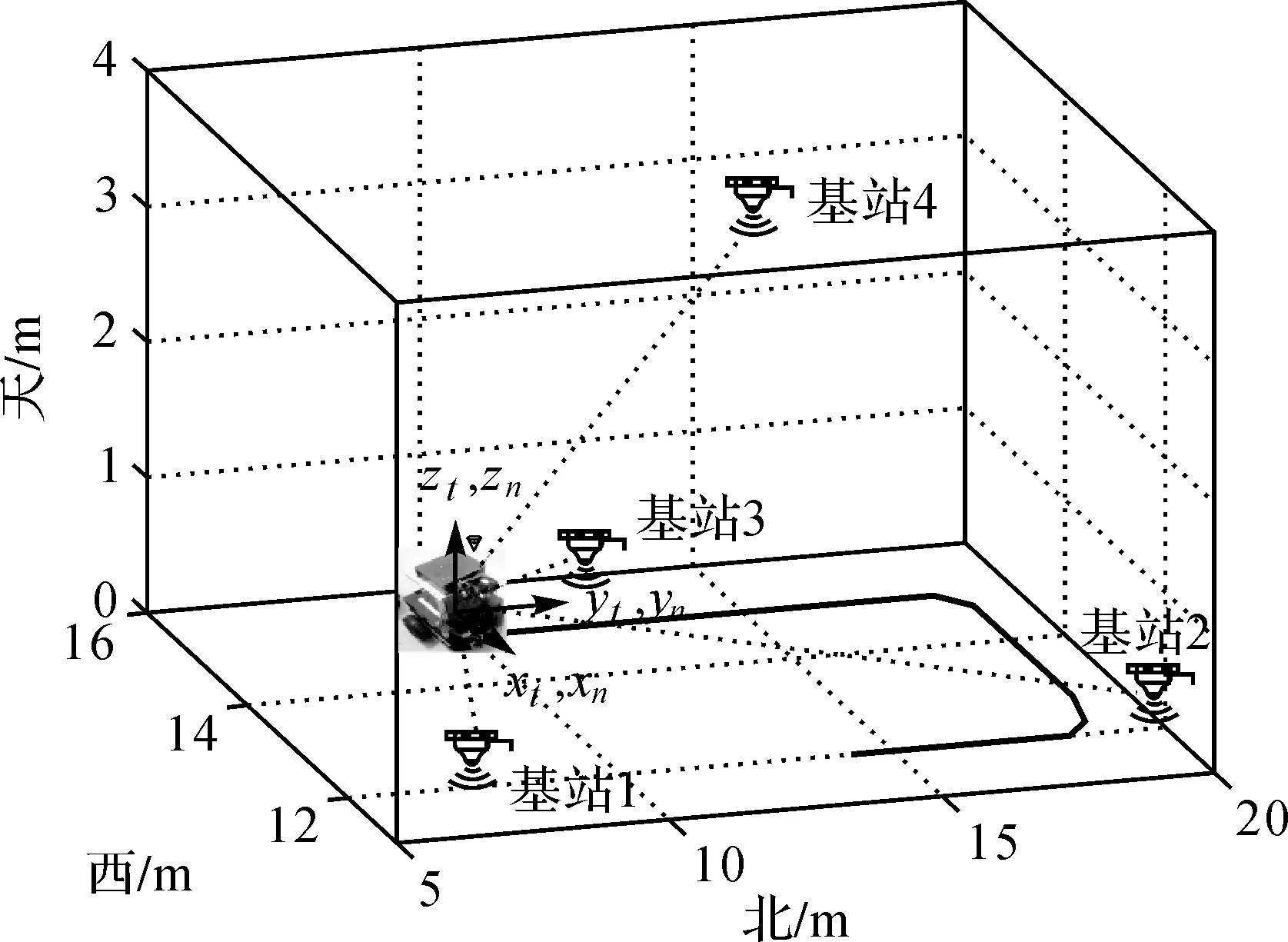
图1 载体轨迹示意图Fig.1 Sketch map of indoor carrier
误差模拟:现假设INS的陀螺与加速度计的常值零偏为零;模拟INS器件的陀螺随机游走误差为0.5°/s,加速度计的随机游走误差10 mg,UWB距离测量值的随机误差为0.01 m;视基站定位的时间测量误差为常值,可将由时间测量误差引起的测距误差作为系统误差,其大小分别为0.4 m、0.4 m、0.6 m、0.6 m;基站的位置误差为0.08 m。
对于姿态参数的计算,通常转化为四元素的更新,以避免航向角为90°时不可解的情况。姿态四元素更新方程为[25]
(47)


(48)

由UWB提供的测距信息以及姿态四元素观测值,建立观测方程为
(49)

初始历元的先验信息如下
Σ0=10-5·I7×7
各历元的系统噪声定为
对于式(48)的状态方程,令vec(φk)=h+Bφk[7],其中h对应于φk中的常值元素,B对应于φk中的个随机元素,则状态转移矩阵φk的方差-协方差阵为
Qφk=BQφkBT
(50)
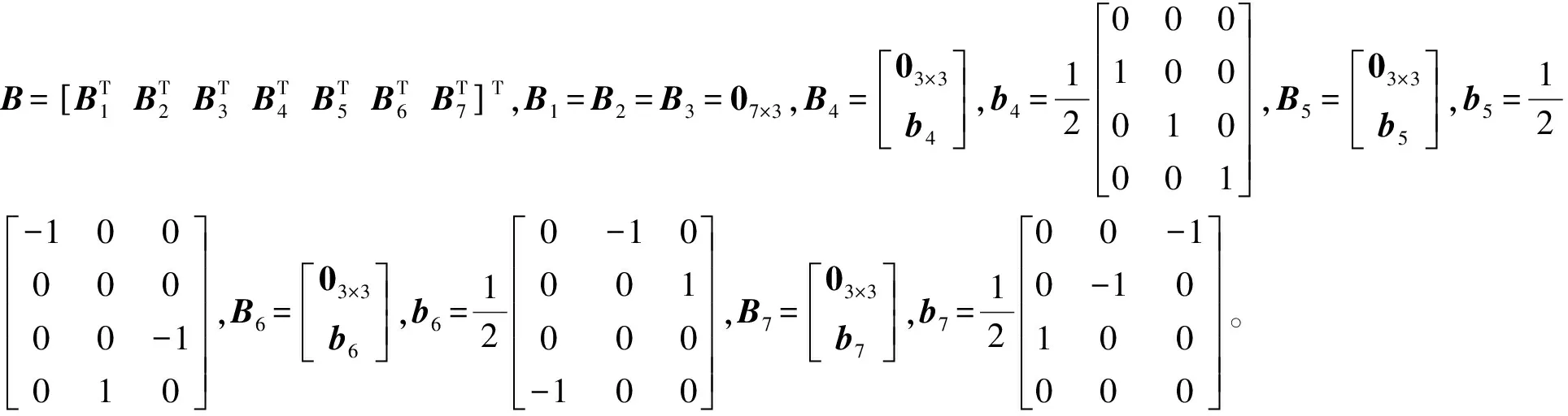
对于式(49)的观测方程,其系数矩阵与观测向量的方差-协方差阵可由文献[10]方法确定,观测向量中的四元素的方差协方差阵设为diag([0.03 0.03 0.03 0.03])。
给真实轨迹与姿态模拟误差,由式(48)、式(49)建立各历元的状态方程与观测方程;采用标准Kalman滤波方法(KF法)、文献[21]方法(WTKF法)与本文方法作对比试验;随机模拟一次误差情况下,不同方法得到的各历元三维位置及姿态参数结果如图2,其中姿态结果由最终估计得到的四元素结果转换而得。

图2 各方法的参数估值Fig.2 The adjustment results of each method
为了更好地进行对比分析,对上述试验模拟计算10 000次,并将各历元载体位置和姿态的平差结果与真值求差并取绝对值,获得平差结果与真值的绝对误差,将10 000次各历元平差参数的实际偏差取均值。三维位置及姿态的绝对误差均值结果见图3。
分析仿真算例的平差结果,可得如下结论:
(1) 由随机模拟一次误差所得结果图2可知,无论是各历元的三维位置估值或是姿态估值,3种方法均能在一定程度上反映真实轨迹与姿态的变化趋势;然而,整体上从各历元的估值结果来看,本文方法所得位置与姿态结果均优于KF法与WTKF法。从图2(a)可知,在位置估值方面,本文方法在北向和西向与KF法和WTKF法所得结果近似度较高;在天向上KF法与WTKF法的结果较差,而本文方法始终能保持较高的解算精度。从图2(b)可知,3种方法的解算结果较好地反映了航向的变化,而在俯仰角和横滚角方面,本文方法的估值结果较优。
(2) 由10 000次试验的均值结果(图3)可知,本文方法估计的各历元位置绝对误差均值与姿态绝对误差均值结果整体上优于KF法与WTKF法,从统计的角度表明了本文方法的有效性;随着历元的增加,3种方法的位置与姿态误差均存在变大的趋势。虽然在某一特定历元,本文方法的误差较之KF法或TKF法要大,但从此历元后所有历元上分析,这并未在很大程度上影响到本文方法对后续历元的解算,可见,由于本文方法同时顾及了状态方程中状态转移矩阵与观测方程中系数矩阵的误差项,相对于只顾及观测方程系数矩阵误差的WTKF法有了一定的改善,平差结果的有效性表明了本文方法是可行的。
(3) 从上述分析可知,由于同时顾及状态方程中状态转移矩阵与观测方程中系数矩阵的误差项,本文方法的数值计算结果优于已有KF和WTKF的结果。由于文献[19]的TKF方法中观测方程系数矩阵的方差-协方差阵须满足特定结构Im⊗Qyk,因此不适合本算例的数值计算。下面从公式推导的角度进行简单说明。假设不考虑状态方程中状态转移矩阵的误差项及状态方程和观测方程中的控制向量,且QAk=Im⊗Qyk,QykAk=QAkyk=0[19]。顾及到符号表达的不同,由文献[19]中式(47)可知,参数估值为
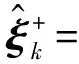
(51)
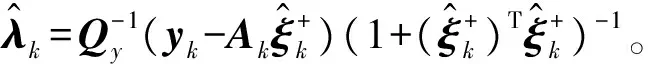
(52)
通过对式(52)进行适当数学变换得

(53)
由矩阵反演公式,式(53)中
(54)
在满足上述假设条件下,结合式(52)—式(54),不难得出式(51)与式(38)相等,也即本文方法参数估值式(38)等价于文献[19]中参数估值式(47)。因此,TKF方法可视为本文方法在满足某些假设情况下的特例。同理,若不顾及状态方程中系数阵误差的影响,不难证明本文方法等价于文献[21]的WTKF方法。
(4) 为了更好地分析,假设状态方程和观测方程中的控制向量为零,在本文动态EIV模型的基础上,分以下4种情况进行对比与归纳:
情况1:不考虑状态转移矩阵误差项影响。
情况2:不考虑状态转移矩阵误差项影响,且观测方程的方差-协方差阵满足特定结构。
情况3:不考虑状态方程。
情况4:不考虑状态方程及参数的先验信息。

综合上述分析,已有TKF须假设观测方程系数矩阵满足特定结构且未顾及状态方程系数阵的误差项,因而其应用范围有限;WTKF方法较之TKF方法,虽然其可处理观测方程中随机元素为一般方差阵的情况,但由于未顾及状态方程中状态转移矩阵的误差,限制了该方法的应用;在某些应用场景中,观测方程的系数阵和状态方程中状态转移矩阵可同时存在误差项影响,因此采用本文方法更为合理。TKF、WTKF与加权总体最小二乘平差结果可视为是本文方法在满足某种条件下的特例,可见本文推导的总体卡尔曼滤波方法是计算状态方程与观测方程均为线性情况下更为通用的一种总体卡尔曼滤波方法。
表1本文方法与已有TKF和WTLS平差方法的对比结果
Tab.1ComparisonoftheproposedmethodwiththeexistingTKFandWTLSmethods

情况对比结果1等价于文献[21]方法2等价于文献[19]方法3等价于文献[8]中方法64等价于文献[8]中方法3及文献[14]方法
3 结 论
本文在已有的动态EIV模型基础上,考虑了状态方程中状态转移矩阵的误差项影响,推导了能够同时顾及状态方程中状态转移矩阵与观测方程中系数矩阵误差的总体卡尔曼滤波方法。本文从公式推导的角度证明了,当观测方程系数矩阵的方差-协方差阵满足特定结构,且不顾及状态方程中状态转移矩阵的误差情况下,本文方法等价于TKF方法;本文推导的参数估值公式具有与标准Kalman滤波公式相似的结构,平差结果简单、易于理解;算例试验验证了本文方法较之WTKF方法与KF方法能取得更优的平差结果,表明了本文方法可行性与有效性。然而本文推导方法仅适用于状态方程与观测方程均为线性的情况,在实际情况下,绝大多数动态模型均呈现非线性的特点,推导适用于非线性动态EIV模型的总体卡尔曼滤波方法将是下一步研究的重点。

图3 各方法绝对误差均值Fig.3 The average values of absolute error by each method
参考文献:
[1] CHANG Guobin. Alternative Formulation of the Kalman Filter for Correlated Process and Observation Noise[J]. IET Science, Measurement & Technology, 2014, 8(5): 310-318.
[2] 杨元喜. 自适应动态导航定位[M]. 2版. 北京: 测绘出版社, 2017.
YANG Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. 2nd ed. Beijing: Surveying and Mapping Press, 2017.
[3] CRASSIDIS J L, JUNKINS J L. Optimal Estimation of Dynamic Systems[M]. 2nd ed. Boca Raton, FL: CRC Press, 2011.
[4] 刘经南. 卫星网与地面网联合平差坐标转换模型的等价性[J]. 武汉测绘学院学报, 1983, 8(1): 37-50.
LIU Jingnan. The Equivalence of Mathematical Models for Coordinate Systems Transformation in the Adjustment for the Combination of Satellite and Terrestrial Network[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1983, 8(1): 37-50.
[5] 刘经南, 刘大杰. 大地坐标和地心坐标精度对联合平差的精度影响[J]. 测绘学报, 1985, 14(2): 133-144.
LIU Jingnan, LIU Dajie. The Influence of the Accuracy in Geodetic and Geocentric Coordinates on the Accuracy in the Results of Simultaneous Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 1985, 14(2): 133-144.
[6] 刘经南, 刘大杰, 崔希璋. 卫星网与地面网联合平差的理论和应用[J]. 武汉测绘科技大学学报, 1987, 12(4): 1-9.
LIU Jingnan, LIU Dajie, CUI Xizhang. Theory and Application of the Combined Adjustment of Satellite and Terrestrial Network[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1987, 12(4): 1-9.
[7] XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675.
[8] FANG Xing. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749.
[9] 曾文宪, 方兴, 刘经南, 等. 通用EIV平差模型及其加权整体最小二乘估计[J]. 测绘学报, 2016, 45(8): 890-894, 903. DOI: 10.11947/j.AGCS.2016.20150156.
ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted Total Least Squares of Universal EIV Adjustment Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 890-894, 903. DOI: 10.11947/j.AGCS.2016.20150156.
[10] JAZAERI S, AMIRI-SIMKOOEI A. Weighted Total Least Squares for Solving Non-linear Problem: GNSS Point Positioning[J]. Survey Review, 2015, 47(343): 265-271.
[11] FANG Xing. Weighted Total Least-squares with Constraints: A Universal Formula for Geodetic Symmetrical Transformations[J]. Journal of Geodesy, 2015, 89(5): 459-469.
[12] FANG Xing, WANG Jin, LI Bofeng, et al. On Total Least Squares for Quadratic form Estimation[J]. Studia Geophysica et Geodaetica, 2015, 59(3): 366-379.
[13] 王乐洋, 余航, 陈晓勇. Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22-29. DOI: 10.11947/j.AGCS.2016.20140560.
WANG Leyang, YU Hang, CHEN Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22-29. DOI: 10.11947/j.AGCS.2016.20140560.
[14] 王乐洋, 余航, 李毅. 一种加权总体最小二乘问题的解法[J]. 中国矿业大学学报, 2016, 45(6): 1263-1270.
WANG Leyang, YU Hang, LI Yi. A Method for Weighted Total Least Squares Problem[J]. Journal of China University of Mining & Technology, 2016, 45(6): 1263-1270.
[15] FANG Xing, LI Bofeng, ALKHATIB H, et al. Bayesian Inference for the Errors-in-variables Model[J]. Studia Geophysica et Geodaetica, 2017, 61(1): 35-52.
[16] WANG Bin, LI Jiancheng, LIU Chao, et al. Generalized Total Least Squares Prediction Algorithm for Universal 3D Similarity Transformation[J]. Advances in Space Research, 2017, 59(3): 815-823.
[17] ZHOU Yongjun, GONG Jinghai, FANG Xing. Accurate Coupled Lines Fitting in an Errors-in-variables Framework[J]. Survey Review, 2017. DOI: 10.1080/00396265.2017.1281095.
[18] LIU Ji, MENDOZA S, LI Guang, et al. Efficient Total Least Squares State and Parameter Estimation for Differentially Flat Systems[C]∥Proceedings of 2016 American Control Conference. Boston, MA: IEEE, 2016: 5419-5424.
[19] SCHAFFRIN B, IZ H B. Towards Total Kalman Filtering for Mobile Mapping[C]∥Proceedings of the 5th International Symposium on Mobile Mapping Technology. Padua, Italy: ISPRS, 2007: 270-275.
[20] SCHAFFRIN B, UZUN S. Errors-in-variables for Mobile Mapping Algorithms in the Presence of Outliers[J]. Archives of Photogrammetry, Cartography and Remote Sensing, 2011, 22(3): 377-387.
[21] MAHBOUB V, SAADATSERESHT M, ARDALAN A A. A General Weighted Total Kalman Filter Algorithm with Numerical Evaluation[J]. Studia Geophysica et Geodaetica, 2017, 61(1): 19-34. DOI: 10.1007/s11200-016-0815-7.
[22] 崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 2版. 武汉: 武汉大学出版社, 2009.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. 2nd ed. Wuhan: Wuhan University Press, 2009.
[23] LI Zengke, CHANG Guobin, GAO Jingxiang, et al. GPS/UWB/MEMS-IMU Tightly Coupled Navigation with Improved Robust Kalman Filter[J]. Advances in Space Research, 2016, 58(11): 2424-2434.
[24] FARRELL J. Aided Navigation: GPS with High Rate Sensors[M]. New York: McGraw-Hill, Inc., 2008.
[25] YUAN Xuebing, YU Shuai, ZHANG Shengzhi, et al. Quaternion-based Unscented Kalman Filter for Accurate Indoor Heading Estimation Using Wearable Multi-sensor System[J]. Sensors, 2015, 15(5): 10872-10890.

