利用微纳结构提高太阳能薄膜电池效率
,
(上海电力学院 能源与机械工程学院,上海 200090)
能源需求与环境保护之间具有一定的冲突,使用可再生能源是一种较好的解决途径[1]。太阳能能量可观,并具有经济性、环境友好性及安全性的特点,使其有潜力成为未来能源[2]。
太阳能电池是目前利用太阳能的最普遍的手段,但吸收率较低一直制约其发展,为解决此问题多种方法被提出[3-4]。目前,大部分方法(如化学腐蚀法、表面粗糙法等)都只能运用于单、多晶硅等厚度较大的太阳能电池,对于厚度只有几微米的太阳能薄膜电池,这些方法不再适用。因此,微纳结构以其独特的光学特性被应用于太阳能薄膜电池来提高效率[5]。微纳结构能激发局域表面等离子体共振(Localized Surface Plasmon Resonance,LSPR)效应以及表面等离子体共振(Surface Plasmon Resonance,SPR)效应,可在特定的波段有效地提高太阳能电池的吸收效率,但依然有些波段无法有效吸收,因此需要其他方法将未能吸收的光利用起来。磁极子激元(Magnetic Polaritons,MPs)效应在光电发射器[6]中已得到应用,并取得了良好的效果。通过调节结构参数,MPs效应可以对LSPR和SPR效应进行有效补充。因此,本文采用Ag圆盘与Ag圆柱结构激发MPs效应,并进一步发现MPs可形成新的吸收峰,可以与LSPR和SPR及光子模式耦合,拓宽吸收峰面积,进一步提升太阳能电池的吸收率。
1 结构设计及模拟方法
本文所提出的Ag圆盘与Ag圆柱结构如图1所示。
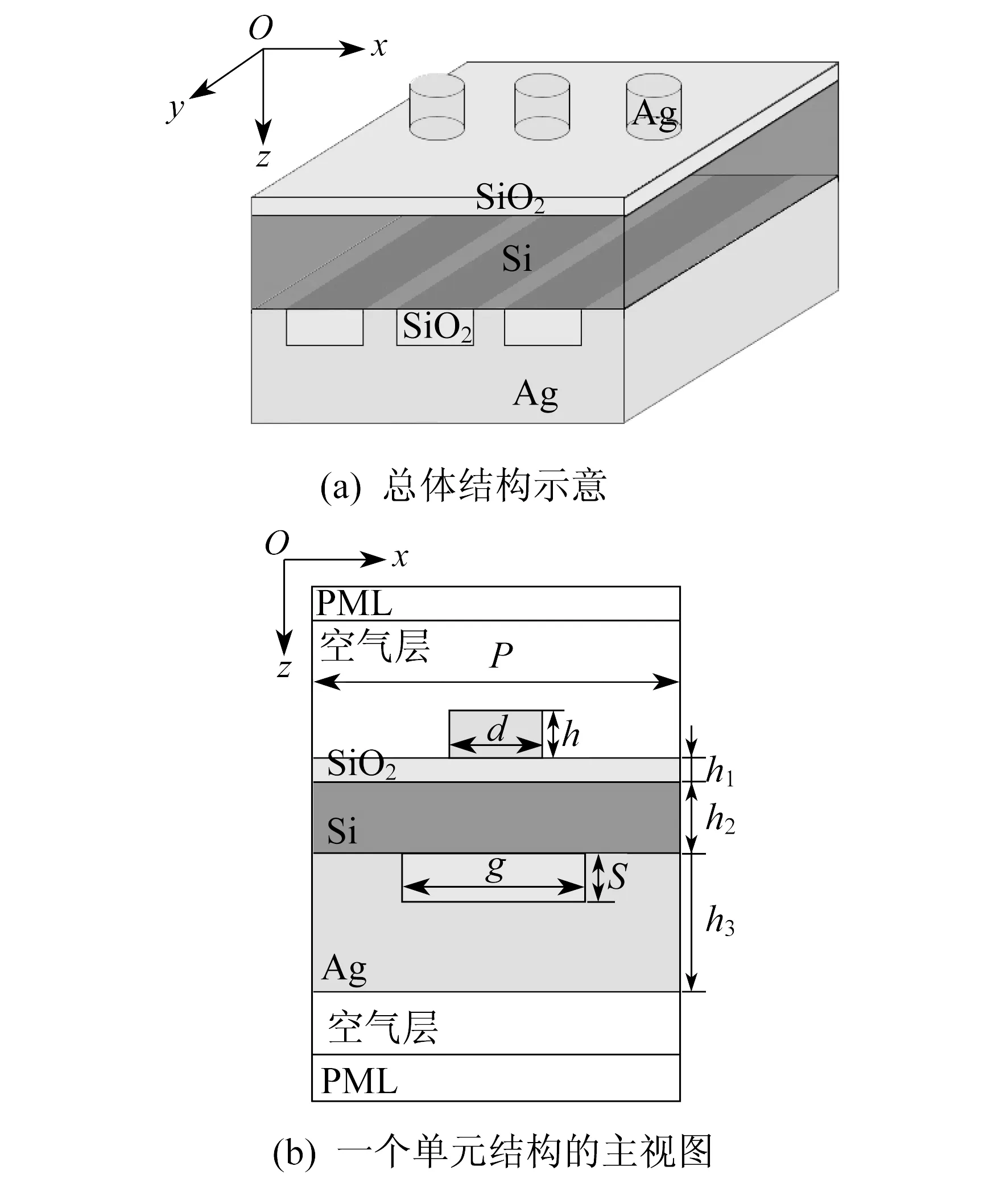
图1 Ag圆盘与Ag圆柱结构示意
由图1(a)可知,该结构从上到下分别为周期性Ag圆柱、SiO2电介质层、Ag圆柱、Si吸收层、周期性Ag光栅结构。图1(b)中,该结构在x轴和y轴上的周期都为P,圆柱直径为d,圆柱半径为r,圆柱高为h,SiO2电介质层厚度为h1,Si吸收层厚度为h2,Ag光栅结构占空比通过SiO2块的宽度g调控,深度通过SiO2长条块的高度S调控,Ag光栅的总高度为h3。因为Si层表面会反射大部分入射光,因此需要加一层SiO2电介质层作为减反层。
通过应用时域有限差分法(Finite Difference Time Domain,FDTD)对模型进行三维数值模拟。在此选择h1=5 nm,h2=80 nm,h3=100 nm,g=150 nm,S=40 nm。为了模拟周期性结构,在x轴和y轴上设置周期性边界条件,在z方向上方和下方设置完美匹配层(Perfectly Matched Layer,PML),使该层介质的波阻抗与相邻介质的波阻抗完全匹配,从而使入射波可以无反射地穿过PML分界面,以此来防止非物理性反射干扰模拟结果。光源为垂直该结构表面入射的太阳光,即电场平行x轴的TM波与电场平行y轴的TE波的混合波。为了确保是Si吸收层而不是上面的纳米结构吸收了太阳光,计算的吸收率都是Si层吸收率。
为了研究该结构的提升效果,将Si吸收层吸收率与大气质量(AM)1.5G条件下太阳辐射强度结合起来考虑,在某一波段下Si吸收层的吸收系数定义为[7]
(1)
式中:A(ω)——Si吸收层某一波段的吸收率;
F(ω)——某一波段的太阳能辐照强度。
这样整体提升系数定义为
(2)
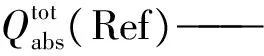
2 结果及讨论
2.1 圆柱尺寸的优化
为了更准确区分各个峰的激发机理,先研究没有加圆盘、周期为280 nm及TM波入射时的情况。首先,研究圆柱对整个结构提升的机理,纳米级圆柱可以激发LSPR效应。为了预测LSPR的激发波长,将尺寸远远小于入射波长λ的圆柱(h=90 nm,d=60 nm),近似为半径r′小于等于40 nm的球体,由于r′/λ<0.1,因此本文对麦克斯韦方程采用准静态近似,从而可以用如下公式计算LSPR的激发波长[8]
(3)
式中:N——有限极化因子;
εout——外部环境的介电常数;
εr,εi——金属介电常数的实数和虚数部分;
χ——形状参数,根据不同的纵横比取不同的值,对于球来说取2。
结合式(3)与FDTD模拟结果分析机理,吸收率随圆柱尺寸的变化趋势如图2所示。
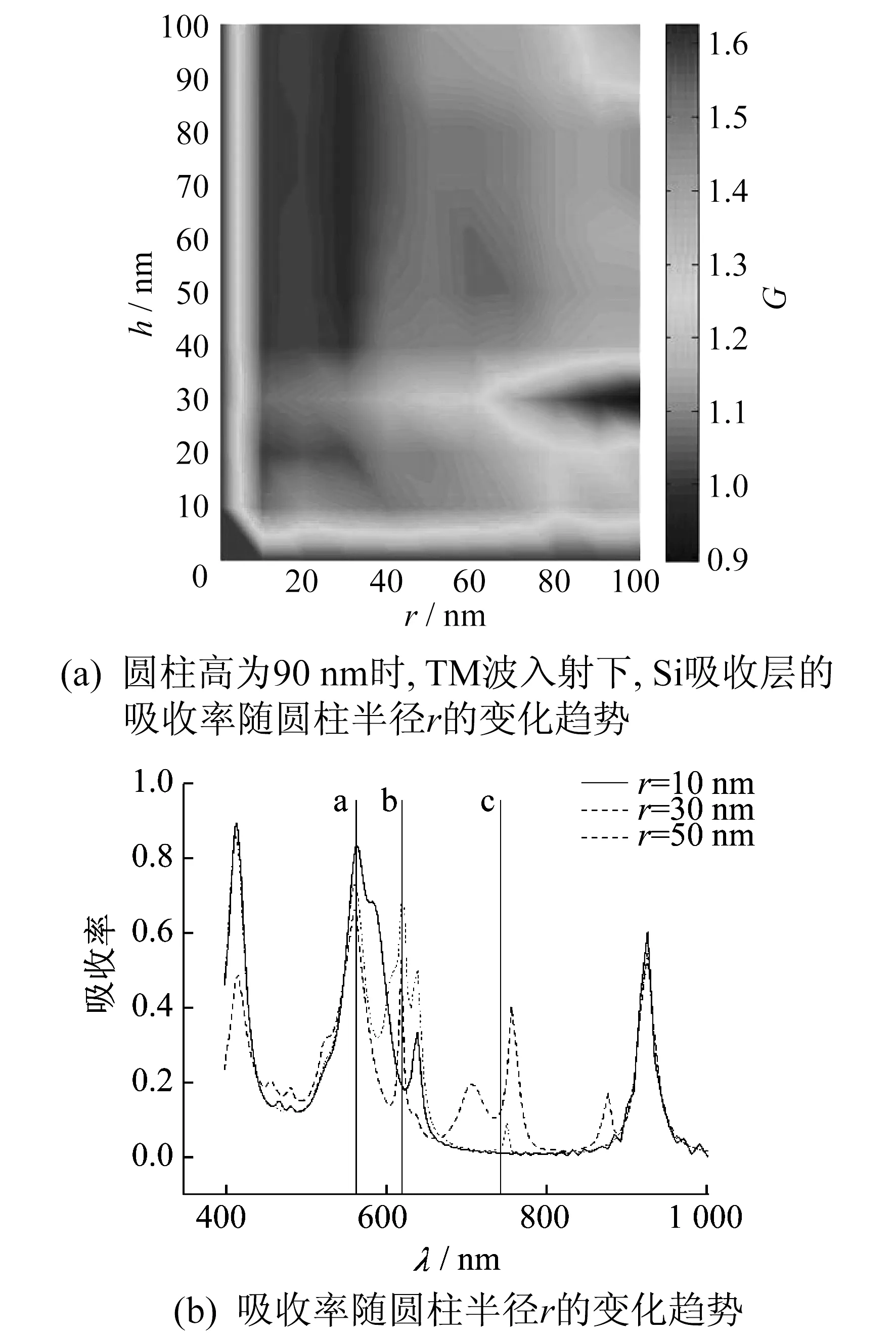
图2 吸收率随圆柱尺寸的变化趋势
由图2(a)可知,在h不变的情况下,G随着r的增加先增加,并在r=30 nm时达到最大值,即颜色达到最深处,然后随着r的增加而减小。结合图2(b),分析产生这一现象的原因:当r=10 nm时,由于圆柱太细,导致LSPR效应所激发的峰矮小,使其对吸收率的增加效果没有那么明显;随着r增大到30 nm,LSPR所激发的峰(b线处)开始变宽且吸收峰扩展到太阳能辐照强度比较强的580~620 nm波段;当r增大到50 nm时,由于圆柱过大影响了Si层本身的吸收率,导致400 nm波段处的吸收率降低,而且由于圆柱变大后不能近似成球形粒子,使得入射光的散射场用矢量球谐波级数展开时高阶多极模式渐显,从而导致了四极子共振模式[9],除了主峰还出现了次峰,同时χ和r′值发生了变化,导致主峰发生了红移(从b线处移至c线处),在此波段的太阳辐射强度相较于600 nm波段较小,因此导致图2(a)中G值下降;当r变得更大时,Si层吸收率更低,峰红移到更长波段,因此在r=30 nm以后,G值随着r的增大而减小。最后本文将圆柱尺寸定为h=90 nm,r=30 nm。
2.2 周期优化及提升机理
2.2.1 TM波
为了使提升系数G达到最大值,模拟Si层吸收率随x方向和y方向结构周期变化的趋势图,同时探究各个峰产生的机理。图3(a)是在TM波入射、400~1 000 nm波段下,Si层吸收率随周期P变化的趋势图,其中周期指的是x轴与y轴周期同时按同一规律变化。图3(a)中,在a,b,c处出现吸收峰,λ=400 nm处的峰是Si本身的吸收峰。
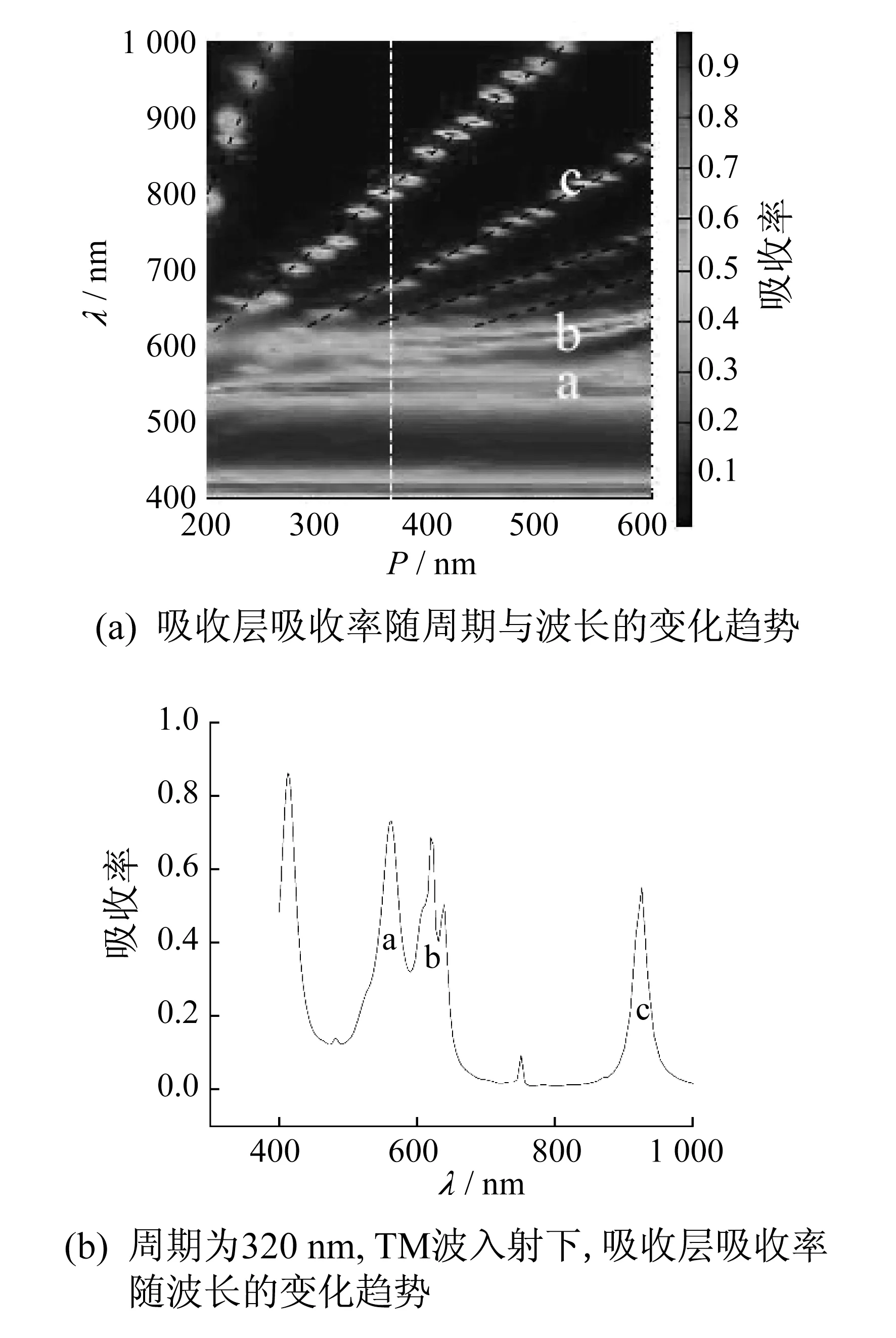
图3 吸收率随周期的变化趋势
由图3(b)可知,a处(λ=550 nm)和b处(λ=600 nm)吸收峰基本不随周期变化而变化。根据式(1)可知,LSPR激发波长与周期关系不大,与圆柱尺寸关系较大。通过观察图3(a)可知,当改变Ag圆柱时,b峰激发波长发生了较大的改变,而a峰激发波长基本没有改变,由此可以确定b峰是LSPR效应所激发的吸收峰,a峰是光子模式[10]所激发的吸收峰,光子模式类似于有限厚度电介质平板中的平面波导模式,其特性取决于Si层厚度。b峰附近(λ=630 nm处)出现了一个b峰的次峰,这是由圆柱产生的四极子共振效应所激发的次峰。c处所形成的吸收峰是由SPR效应产生,该效应会导致表面波在金属与电介质交界处传播。图3(a)中,c线上的吸收峰随着周期的变化并不连续,这是因为沿光栅表面产生SPR的条件如下
(4)
(5)
式中:kx——入射光波长;
ω——入射光的频率;
c——光速;
θ——入射光从空气中照射至光栅的角度;
ε——介电常数;
kSPR——SPR波的波长;
v——任意整数;
A——光栅常数。
图3(a)中黑色虚线分别代表SPR效应的1,2,3,4,5阶,可以看出c处吸收峰是由结构底部的Ag光栅所激发的SPR效应引起的。图3(a)中白色虚线处(P=380 nm)使吸收层在TM波照射下的吸收光子数达到最大值。
2.2.2 TE波
太阳光是TM波和TE波的结合体,因此探究TE波入射时结构的表现非常必要。 当TE波入射时,光栅结构只在x轴方向有周期性,在y轴方向无法形成光栅结构,因此SPR效应无法激发。由于圆柱在x-y轴的对称性,TM波和TE波都能激发LSPR效应。光子效应特性取决于Si层厚度,因此也能够激发。TE波入射下吸收率随周期的变化趋势如图4所示。图4(a)中,黑色虚线1和2处的吸收峰产生的原因,无法用LSPR和光子效应解释,为了解释这些吸收峰,用相同条件对不带光栅的结构做了模拟,结果如图4(b)所示。由图4(b)可以确定这是由光子效应与LSPR效应造成的。因此,我们认为光栅是造成图4(a)中吸收峰的主要原因。
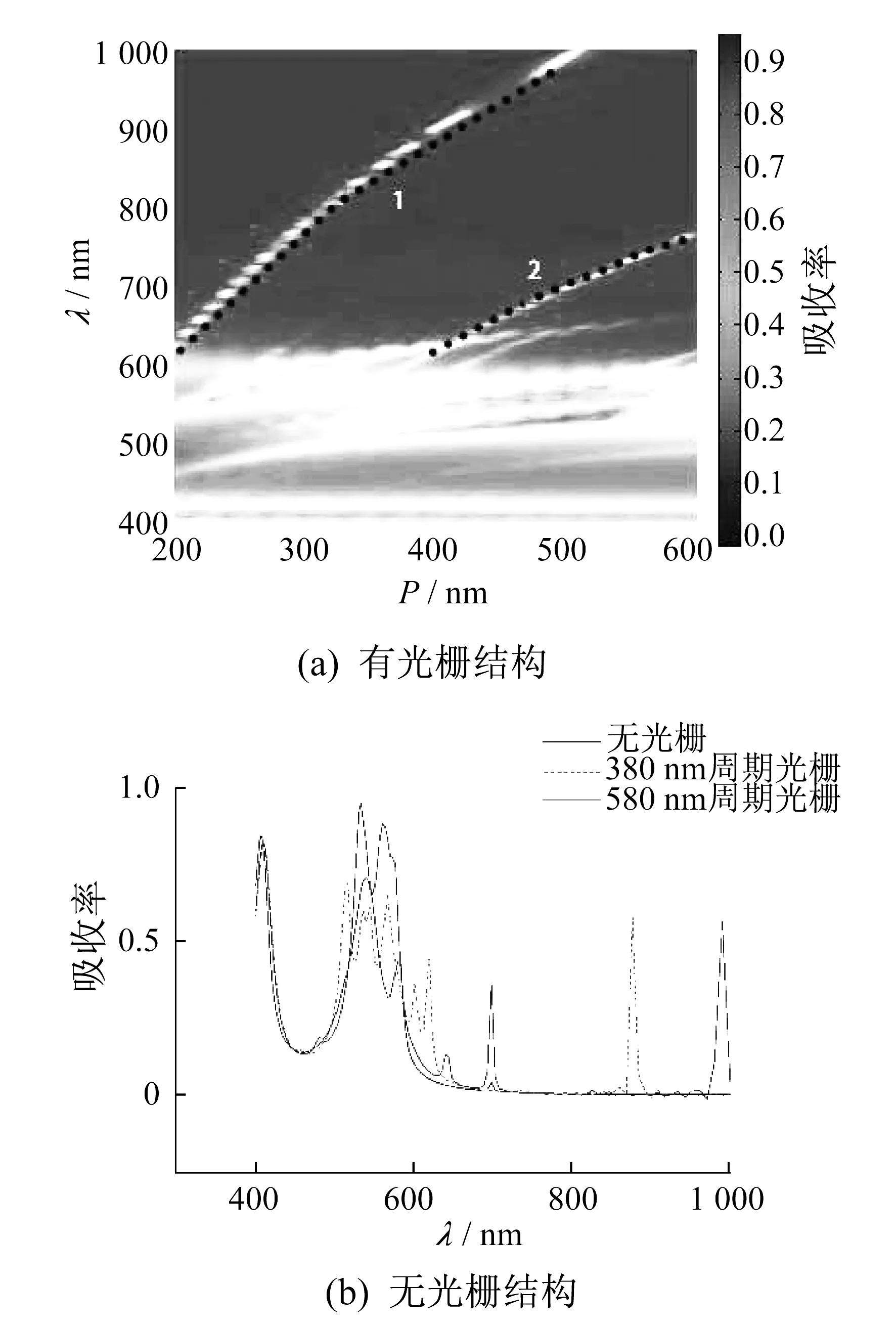
图4 TE波入射下吸收率随周期的变化趋势
为了研究形成机理,对500 nm周期、波长1 000 nm、x轴为250 nm时带光栅结构和不带光栅结构的电场y-z截面图进行分析。由于SiO2光栅两边都是Ag金属,可以将一个光栅周期看做对称双面金属包裹介质波导,这种结构会引发类Farber腔谐振[11],从而可以用以下公式来预测谐振激发波长
(6)
式中:H——光栅的长度;
neff——有效折射率,在此取1.422。
根据式(6)可计算出当周期为500 nm时Farber腔谐振波长为947 nm,710 nm,且激发波长随着周期减小而减小,该结果与FDTD方法模拟出的结果基本一致,由此可知图4(a)中黑线1和2处的吸收峰是由类Farber腔谐振造成的。
2.3 MPs效应的激发
MPs效应指的是微/纳米结构与外电磁波互相耦合从而引发强烈磁共振的现象。为了激发MPs效应,需要加入Ag圆盘。本文中的结构尺寸如下:圆柱半径r=30 nm,圆柱高度h=90 nm,周期P=380 nm。加入圆盘后Si层吸收率随圆盘高度及波长的变化趋势如图5所示。
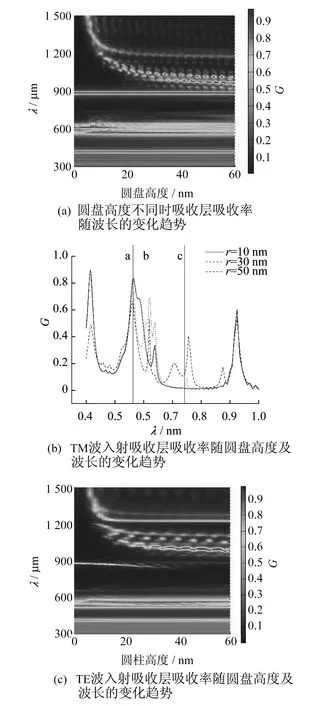
图5 MPs效应对吸收率影响示意
通过观察图5(a)和图5(b)可知,随着圆盘高度的增加,MPs效应所激发的吸收峰将会蓝移,文献[12]中LC模型很好地模拟了MPs的激发波长,因此本文也用LC模型结合FDTD模拟结果解释这一变化的原因。LC模型如图6所示。
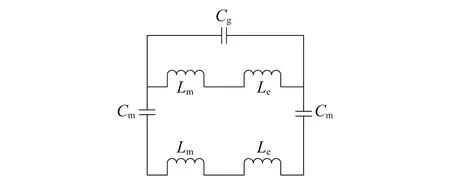
图6 LC模型等效电路
其中介质层可等效为电容Cm,相邻圆柱间的空气间隔可以等效为电容Cg,Ag圆盘和Ag圆柱可等效为电感,电感由自感Le与互感Lm组成,自感主要由电子漂移引起,公式如下
(7)
Lm=0.5μ0t
(8)
(9)
(10)
式中:μ0——真空磁导率;
t——圆盘高度;
R——圆柱的有效截面积,由于电流在圆柱中的不对称性和趋肤深度引起圆柱的截面积只能取有效值,其值小于1,在此取2/3[12];
ωp——Ag的共振频率;
ε0——为真空介电常数;
C1——电荷分布情况,在此取值0.222;
εd——SiO2层的介电常数。
总阻抗公式如下
(11)
当总阻抗为零时,MPs效应发生。根据LC模型预测圆盘高度为58 nm时,吸收峰在974 nm左右出现,模拟结果与FDTD相近。通过LC模型可知,随着圆盘高度的增加,吸收峰将会蓝移,与图5(b)相符,当圆盘高度高于40 nm后,蓝移趋势减缓,吸收峰趋于980 nm左右。当圆盘高度大于30 nm后,由于MPs吸收峰和SPR吸收峰靠近,两种效应互相耦合,会在两峰之间(t为58 nm和40 nm,λ为900 nm处)产生许多次峰,从而使吸收率进一步提高。无圆盘结构(t为零)与有圆盘结构(圆盘高度分别为20 nm,40 nm,58 nm)在580 nm波段时进行比较,可以看出LSPR吸收峰与波导效应吸收峰也受到MPs效应的干扰,使两峰之间产生了若干次峰,提高了吸收效率。圆盘高度为58 nm时吸收效果最好。由图5(c)可知,TE波入射时因为结构对称,依然可以激发MPs效应,但是由于圆盘的加入,破坏了类Farber腔谐振产生的条件,因此无类Farber腔谐振峰,由于是TE波入射,在波长900 nm左右被TM波激发的SPR峰也没有出现。
2.4 最终效果
本文所提出的结构成功激发了LSPR,SPR,光子模式,MPs效应,使太阳能薄膜电池的吸收率得到了提高。为了研究该结构具体的提升效果,本文用总体提升系数Gtot评估系统。由于太阳光中TM波和TE波占比一样,因此总体提升系数Gtot计算式为
(12)
式中:GTM,GTE——在TM波和TE波入射下,波段为400~10 000 nm时,加了圆盘结构的提升系数。
由式(2)计算得到GTM为2.6,GTE为2.18。因此,总体提升系数Gtot为2.39。
3 结 论
(1) 本文通过将LSPR,SPR,光子模式以及MPs效应应用在太阳能非晶硅电池中,使电池吸收率提高2.39倍。
(2) 当将Ag圆柱置于太阳能电池顶部时,Ag圆柱会激发LSPR效应从而使能量被捕捉,LSPR的激发波段可以通过Ag圆柱的半径及周期调节,但是Ag圆柱的高对LSPR的激发波长影响不大。
(3) TM波入射底部Ag光栅时可以激发SPR效应,可以通过调节底部光栅的周期来调节SPR的激发波段,同时底部光栅还会起到波导作用从而使吸收率提升。当TE波入射时,SPR效应无法激发,但会激发一种类似Farber腔谐振的效应,使光波在光栅之间震荡,从而出现一个吸收峰。
(4) 当在太阳能电池中部加一个Ag圆盘后,其与结构上部的Ag圆柱及二氧化硅构成了一个金属-电介质-金属的结构,从而可以激发MPs效应。MPs效应的激发峰主要与两个Ag结构的尺寸有关,可以通过LC等效模型对其激发波段进行预测并指导优化。
参考文献:
[2] JAMAR A,MAJID Z A A,AZMI W H,et al.A review of water heating system for solar energy applications[J].International Communications in Heat and Mass Transfer,2016,76:178-187.
[3] GREEN M A.Lambertian light trapping in textured solar cells and light-emitting diodes:Analytical solutions[J].Progress in Photovoltaics Research & Application,2002,10(4):235-241.
[4] FAHR S,ROCKSTUHL C,LEDERER F.Engineering the randomness for enhanced absorption in solar cells[J].Applied Physics Letters,2008,92(17):65.
[5] ATWATER H A,POLMAN A.Plasmonics for improved photovoltaic devices[J].Nature Materials,2010(9):205-213.
[6] XIA M,ZHANG P,QIAO K,et al.Coupling SPP with LSPR for enhanced field confinement:a simulation study[J].Journal of Physical Chemistry,2016,120(1):527-533.
[7] ZHAO B,WANG L,SHUAI Y,et al.Thermophotovoltaic emitters based on a two-dimensional grating/thin-film nanostructure[J].International Journal of Heat and Mass Transfer,2013,67(12):637-645.
[8] AKIMOV Y A,KOH W S.Design of plasmonic nanoparticles for efficient subwavelength light trapping in thin-film solar cells[J].Plasmonics,2011,6(1):155-161.
[9] WILLETS K A,VAN DUYNE R P.Localized surface plasmon resonance spectroscopy and sensing[J].Annu.Rev.Phys.Chem.,2007,58(1):267-297.
[10] KELLY K L,CORONADO E,ZHAO L L,et al.The optical properties of metal nanoparticles:the influence of size,shape,and dielectric environment[J].Journal of Physical Chemistry B,2003,107(3):668-677.
[11] FERRY V E,SAWEATLOCK L A,PACIFICI D,et al.Plasmonic nanostructure design for efficient light coupling into solar cells[J].Nano Letters,2008,8(12):4391-4397.
[12] WANG Y W,LIU M L,LIU R J,et al.Fabry-perot resonance on extraordinary transmission through one-dimensional metallic gratings with sub-wavelength under transverse electric wave excitation[J].Acta Physica Sinica,2011,60(2):4030-4035.

