弯管内纳米流体非线性特性模拟与分析

, ,,

(上海电力学院 能源与机械工程学院,上海 200090)

随着科学技术的发展,实际生产过程的分析日益精密,各种精确的分析和科学实验的结果表明,任何一个实际的物理系统都是非线性的。传热学各相关学科领域存在着丰富的非线性特性。弯管作为一种特殊的管道,应用在工业生产的方方面面,通过对弯管内流动和非线性特性的研究,可以丰富传热学的物理机理。大量的研究表明,当某个控制参数变化时,非线性特性会出现局部失稳、振荡、多解等复杂的现象。

20世纪中叶,研究者通过模拟和实验的方法发现弯管内存在四涡形式的二次流动,并展开了对弯管内流动分叉、振荡等非线性现象的研究[1-2]。LUO W J[3]分析了长宽比为1及曲率半径为1.5的弯管内的流动,找到了2涡、4涡、6涡及不对称的4种流场状态。张昆等人[4]采用紧致方法对方腔内Rayleigh-Benard对流(自然对流)及其静态分岔现象进行了模拟研究。数值计算结果显示,当长宽比为8时,不同的初场可以得出3种不同的流场和温度场。郑建城等人[5]对封闭圆内开缝圆自然对流的非线性特性进行了研究,结果表明,在不同参数下流动和换热存在稳态定常解、周期性振荡解、拟周期性振荡解和非周期性振荡解。LIU F等人[6]研究了小弯曲曲率矩形通道内充分发展段强制对流的分岔和稳定性,结果发现了7个对称解分枝和4个非对称解分枝,而且随De数(De数为无量纲控制参数)的增加,有限随机扰动导致流体经历从稳态到另一个稳态、周期振荡、间歇振荡、另一个周期振荡、混沌振荡的非线性流动状态。薛雷[7]采用伽辽金方法模拟了方形弯管内充分发展的稳态、层流流动,结果得出曲率为0.2的方形弯管内二次流出现4涡结构的分叉点是Re为300.1。

本文采用欧拉-拉格朗日两相流法模拟了方形弯管内两种不同形状的氧化铝-水纳米流体的非线性特性。在两相流法中,直接设置颗粒和基液的物性参数,同时考虑血小板形和球形的实际尺寸,分析两种不同颗粒形状的非线性特性。

1 数值模型

1.1 几何模型

本文以文献[8]中的方形弯管为几何模型进行对流换热模拟。模型为三维270°截面为方形的弯曲管道。其尺寸如下:水力直径Dh=8 mm,弯管半径Rc=400 mm,曲率δ=Dh/Rc=0.02,半径比Rc/Dh=50。对方形弯管建立环形坐标系(R,Z,θ),其中R和Z表示弯管截面上的坐标,θ表示沿弯管轴线方向的转动角度。弯管的几何结构如图1所示。a表示方形弯管截面的边长。

弯管内采用体积分数为0.5%的γ-Al2O3-去离子水纳米流体作为流动工质,纳米颗粒分别为血小板形和球形的γ-Al2O3,颗粒粒径均为30 nm。本文假设方形弯管内的去离子水与氧化铝纳米颗粒处于热平衡状态,同时纳米流体为牛顿不可压缩流体而且流动状态为层流;纳米流体的热物性为常量;液体在壁面处无滑移。纳米颗粒和去离子水的物性参数如表1所示。血小板形和球形纳米颗粒的不同尺寸如表2所示。

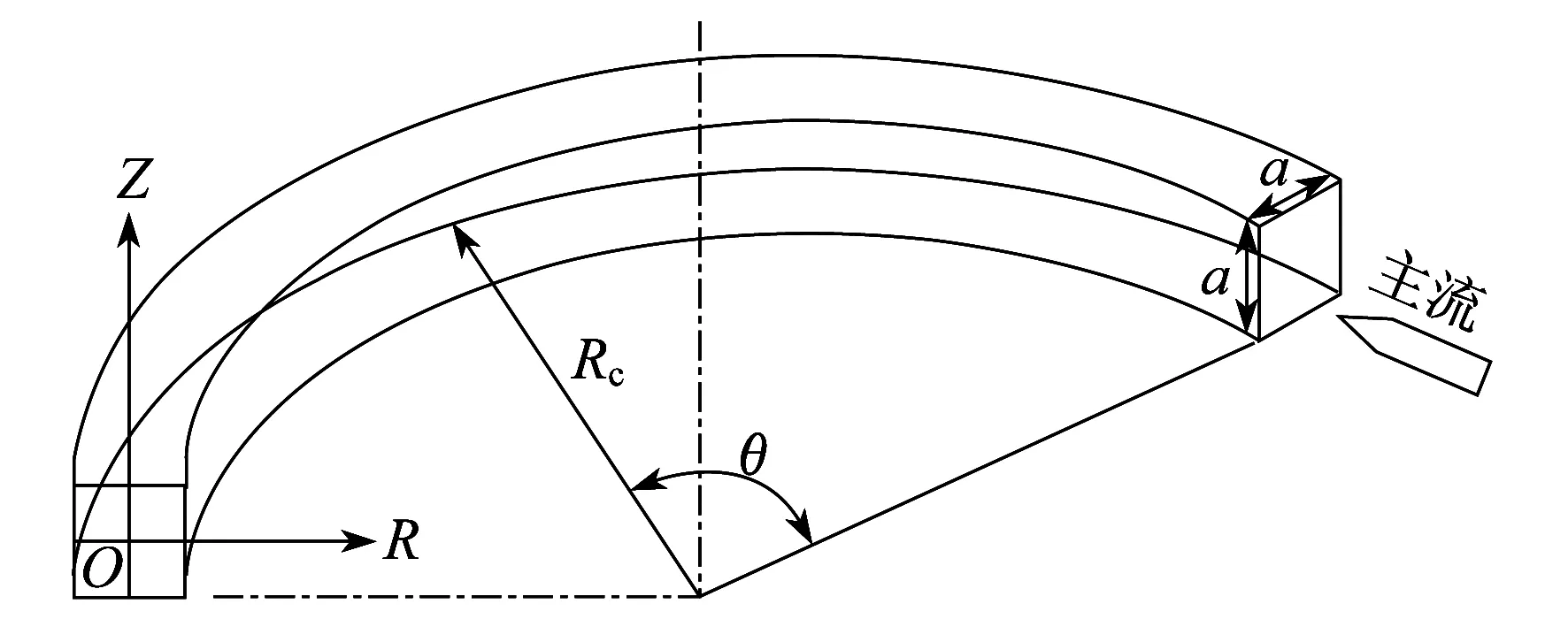
图1 方形截面弯管结构示意

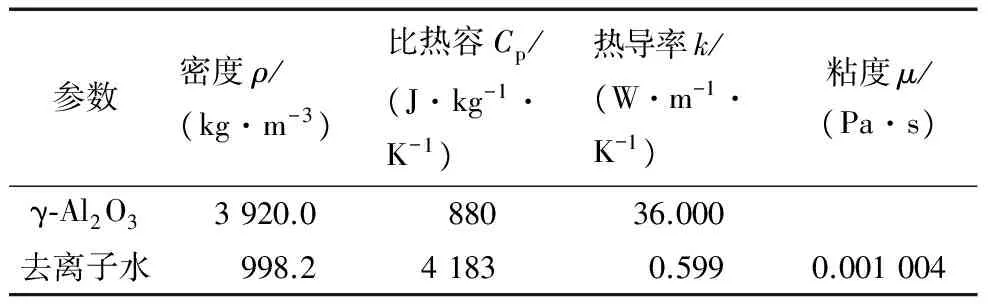
表1 γ-Al2O3和水的物性参数

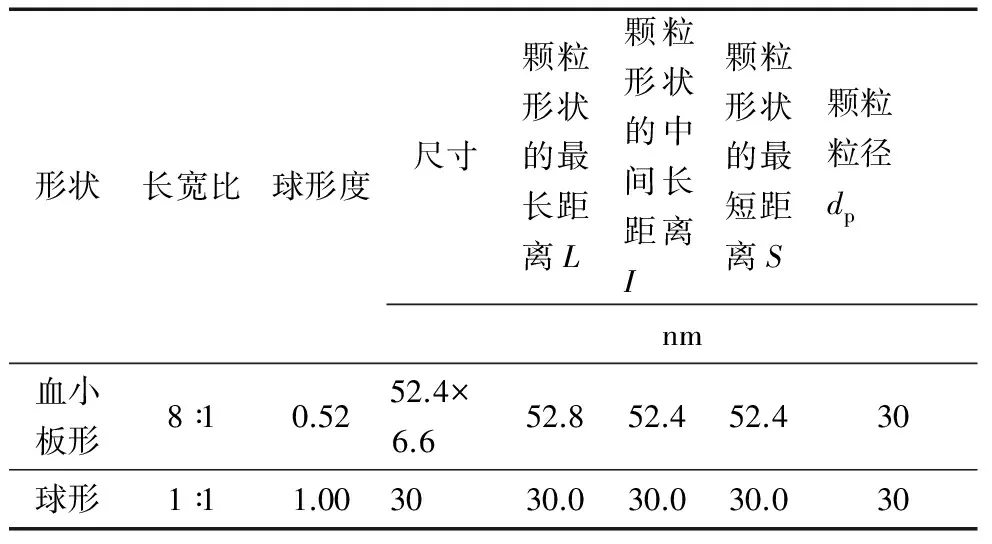
表2 血小板形和球形纳米颗粒的尺寸

1.2 控制方程

质量方程为

(1)

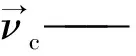
动量方程为

(2)

(3)

式中:ρc——液体密度,kg/m3;

g——重力加速度,m/s2;

μc——液体粘度,Pa·S;

Sm——动量源相;

δV——单元体内颗粒的数量;

mp——颗粒质量,kg;

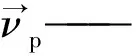
能量方程为

ρc(λcTc)+Sh

(4)

(5)

式中:cpc——液体比热容,J/(kg·K);

Tc——液体温度,K;

λc——液体导热系数,W/(m·K);

Sh——能量源相;

hcp——颗粒表面传热系数,W/(m2·K);

Tp——颗粒温度,K。

1.3 数值模拟方法

本文利用FLUENT14.5软件在层流范围内对方形弯管进行数值模拟,采用欧拉-拉格朗日法的离散项模型(Discrete Phase Model,DPM)对方形弯管内的纳米流体对流换热进行模拟计算。依据血小板形纳米颗粒的实际尺寸,通过编写相应的编程文件,导入到FLUENT中进行模拟计算。

对所研究模型的无量纲控制方程采用SIMPLE算法进行求解,动量方程和能量方程采用二阶迎风格式,使计算具有较高的精度。对于所研究的问题,当能量方程的残差小于10-7时视为计算收敛。

1.4 边界条件

边界条件设置如下:进口条件设置为速度入口,速度大小依据Re来确定,其方向垂直于弯管的截面;出口条件采用压力出口;壁面条件为无滑移边界条件,方形弯管壁面的热流密度设置为5 000 W/m2,弯管的材质为铜管。

2 模拟计算结果与讨论

本文模拟分析弯管内纳米流体对流换热在充分发展段内的非线性特性。文献[2]研究了层流范围内5种不同形状的纳米颗粒对弯管内传热和流动的影响,并指出血小板形的换热能力最强。本文以血小板形纳米流体为例进行了非线性研究,同时与球形纳米流体进行对比,旨在研究弯管内不同De数下不同形状纳米颗粒对流换热在充分发展段内的非线性特性。其中,De数的计算公式为

(6)

式中:δ——曲率。

2.1 血小板形纳米流体的非线性特性

2.1.1 血小板形纳米流体不同解分枝的结构

本文对De数从84.85到325.3(Re范围为600～2 300)的各个工况进行了模拟计算,分析了弯管内充分发展段的分岔和多解结构。结果得出,弯管内血小板形纳米流体存在3个不同的解分枝。为了清楚分析管内充分发展段的流动结构情况,选取了管内某点的速度值v随控制参数De数变化明显的点进行观察监测。本文选取了充分发展段内的某个点(R=0.7 mm,Z=-0.25 mm)的速度值进行观察分析。

图2为点(0.7,-0.25)的速度v随De数的变化情况。从图2可以明显看出,相同De数下,弯管内血小板形纳米流体对流换热存在3种不同的解。随着De数的增大,在7个不同De数下出现了3种不同的解。

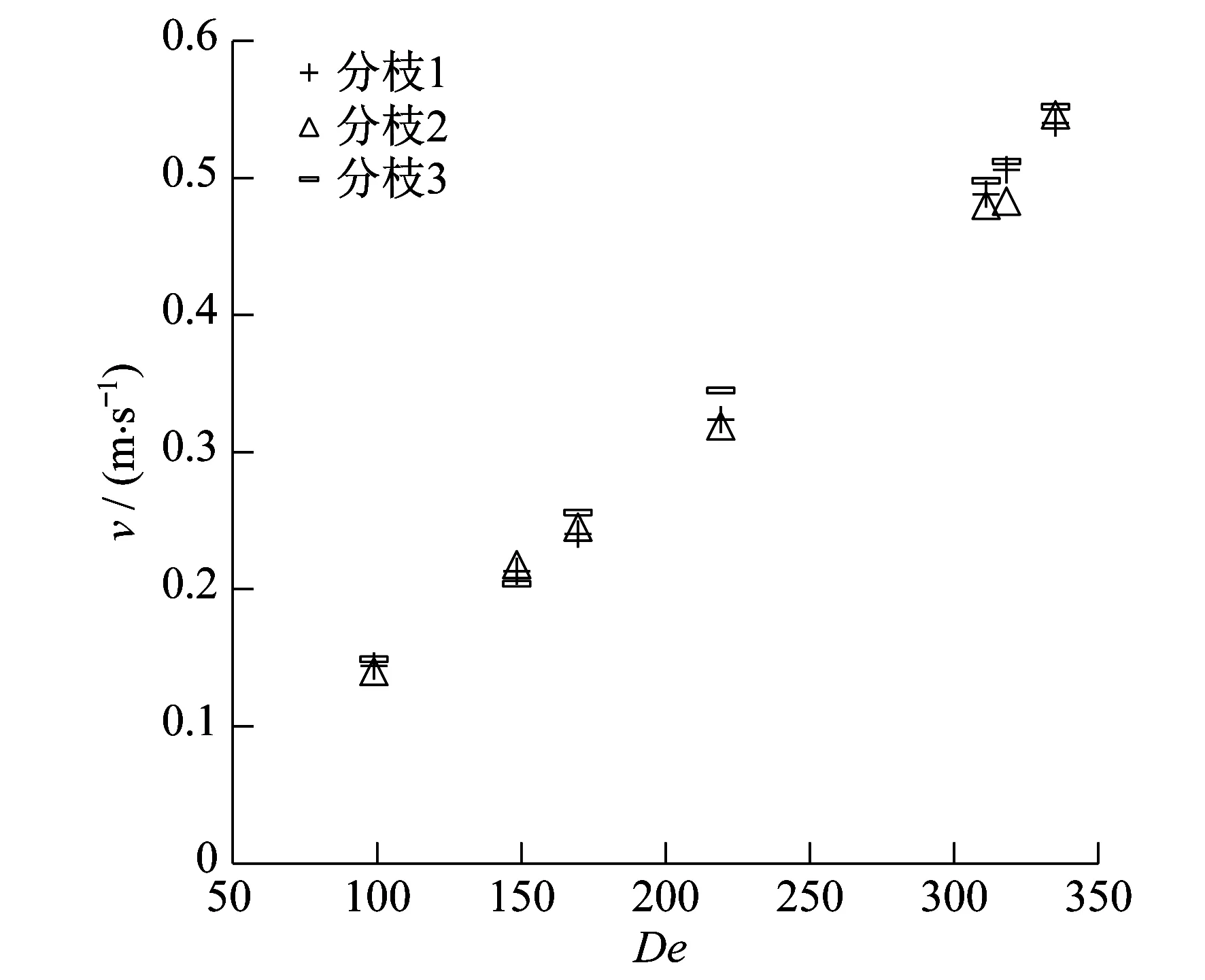
图2 方形弯管内血小板形纳米流体对流换热的不同解分枝

2.1.2 血小板形纳米流体的努塞尔数和摩擦系数

在弯曲通道内,旋涡的位置、形状、大小对轴向速度和温度分布具有很大的影响。由于努塞尔数和摩擦系数依赖于流场和温度场,它们的局部分布和平均值将受到流动多解性的强烈影响。多样性的流动结构导致努赛尔数和摩擦系数在相同De数下的分布可能不同。以下将对努塞尔数和摩擦系数的平均分布和局部分布进行分析。

首先,分析努塞尔数和摩擦系数的平均分布。

图3为血小板形纳米流体3种不同解分枝上的平均努塞尔数Num和平均摩擦系数fm的分布图。由图3中可以看出,相同De数下,弯管内血小板形纳米流体对流换热的Num和fm出现了不同解的分枝,这是由于纳米流体对流换热过程中,纳米流体的局部轴向速度和温度梯度处在不断的变化中,导致同一De数下存在不同的解,表明弯管内血小板形纳米流体对流换热存在多解的非线性。

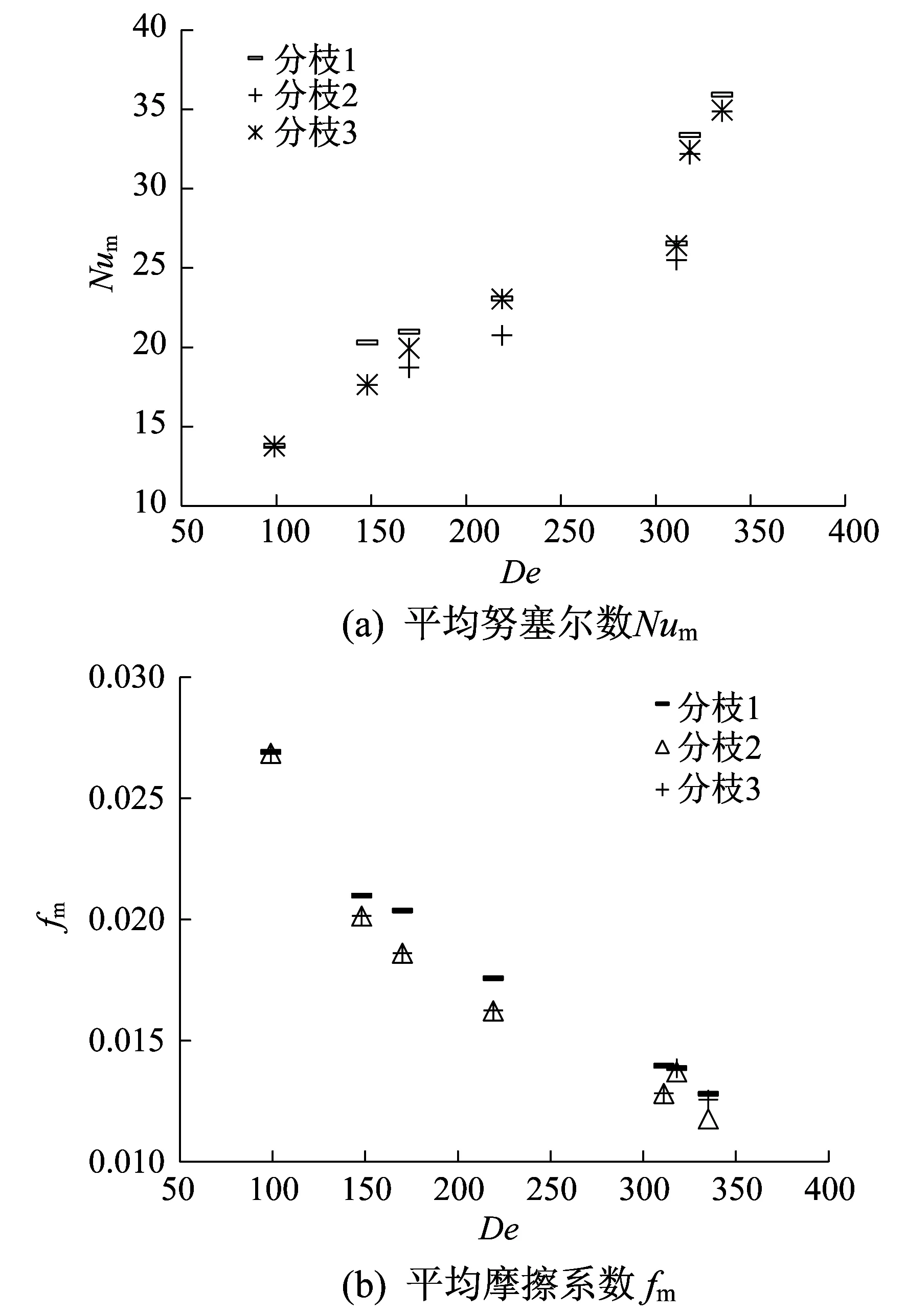
图3 弯管内血小板形纳米流体平均努塞尔数Num和平均摩擦系数fm随De数的变化情况

分析图3(a)中的3个不同解的分枝可知,分枝1的Num最高,分枝2的Num最低。当De数分别为148(Re=1 050),170(Re=1 200),219(Re=1 550)时,分枝1的Num比分枝2分别提高了15.2%,12.1%,11.2%;分枝3的Num比分枝2分别提高了0.2%,6.6%,11%。

图3(b)中,分枝1的fm最高,分枝2的最低。当De数分别为148(Re=1 050),170(Re=1 200),219(Re=1 550)时,分枝1的fm比分枝2分别提高了4.2%,9.4%,8.3%;分枝3的fm比分枝2分别提高了0.05%,0.01%,0.12%。

其次,分析努塞尔数和摩擦系数的局部分布。

图4为血小板形纳米流体解分枝1上的弯管出口截面沿外壁面的局部努塞尔数NuL和局部摩擦系数fL的分布图,横坐标z为无量纲坐标,表示出口截面外壁面坐标Z与弯管水力半径(Dh/2)的比值。

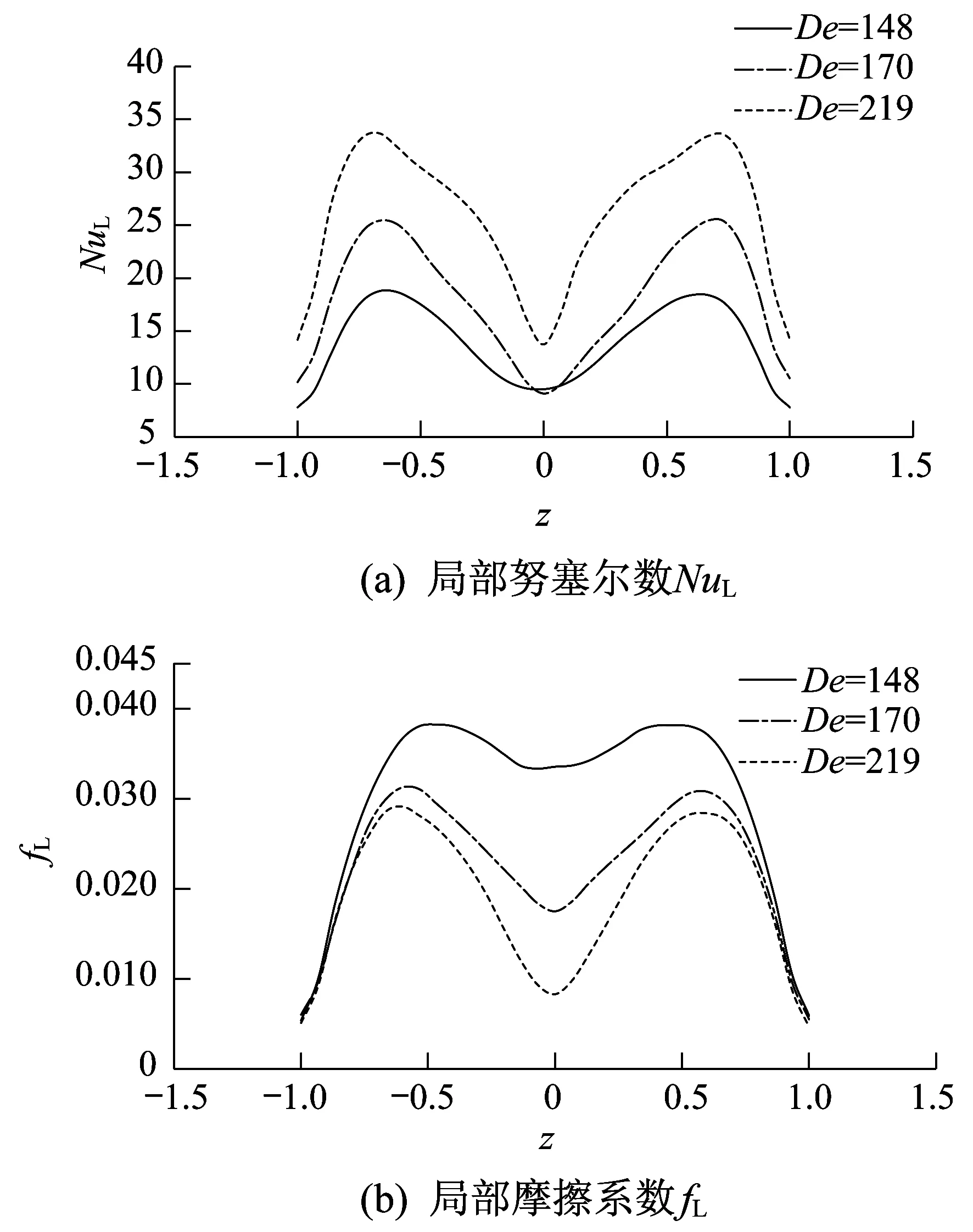
图4 血小板形纳米流体弯管出口截面沿外壁面的局部努塞尔数NuL和局部摩擦系数fL的分布

从图4(a)来看,沿外壁方向,弯管出口截面外壁面的NuL基本呈对称分布,外壁中心处的NuL较低。因弯管二次流和外壁面附近迪恩涡的作用,导致弯管外壁面NuL出现两个峰值,随着De数的增大,两个峰值也相应变大。这是由于随着De数的增大,弯管出口截面中心处的速度也在变大,弯管转弯处的外侧管壁附近速度下降,离心力减小,引起流体从管中心向外侧的附加流动(即二次流),二次流的作用也相应地增强,从而导致峰值随De数增加而变大。

图4(b)显示出了与图4(a)相似的变化情况。沿外壁方向,出口截面沿外壁面的fL呈对称分布,弯管管壁中心处的fL较低,上下壁面附近的密集等速线以及外壁面附近的迪恩涡共同作用使得fL出现两个峰值。

2.2 球形纳米流体的非线性特性

2.2.1 球形纳米流体不同解分枝的结构

图5为球形纳米流体对流换热的点(0.7,-0.25)的速度v随De数的变化情况。图5显示出了3种不同的解分枝。随着De数的增大,在7个不同的De数下出现了3个解分枝。

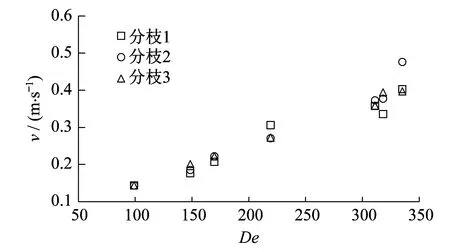
图5 方形弯管内球形纳米流体对流换热的不同解分枝

2.2.2 球形纳米流体的努塞尔数和摩擦系数

图6和图7分别为弯管内球形纳米流体平均努塞尔数Num和平均摩擦系数fm随De数的变化情况。

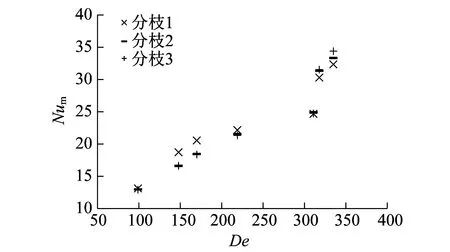
图6 弯管内球形纳米流体平均努塞尔数Num随De数的变化情况

与图5的对比类似,球形纳米流体的Num在7个不同的De数下出现了3个解分枝。并且通过对比图3,图6和图7可以看出,同一De数下,血小板形纳米流体的平均努塞尔数和平均摩擦系数均高于球形纳米流体,这也同文献[2]中的研究结果相符合。

由于血小板形纳米颗粒的实际尺寸要大于球形,因此在对流换热过程中血小板形纳米颗粒与基液之间的相互作用要强于球形,从而血小板形纳米流体的Num和fm要高于球形。

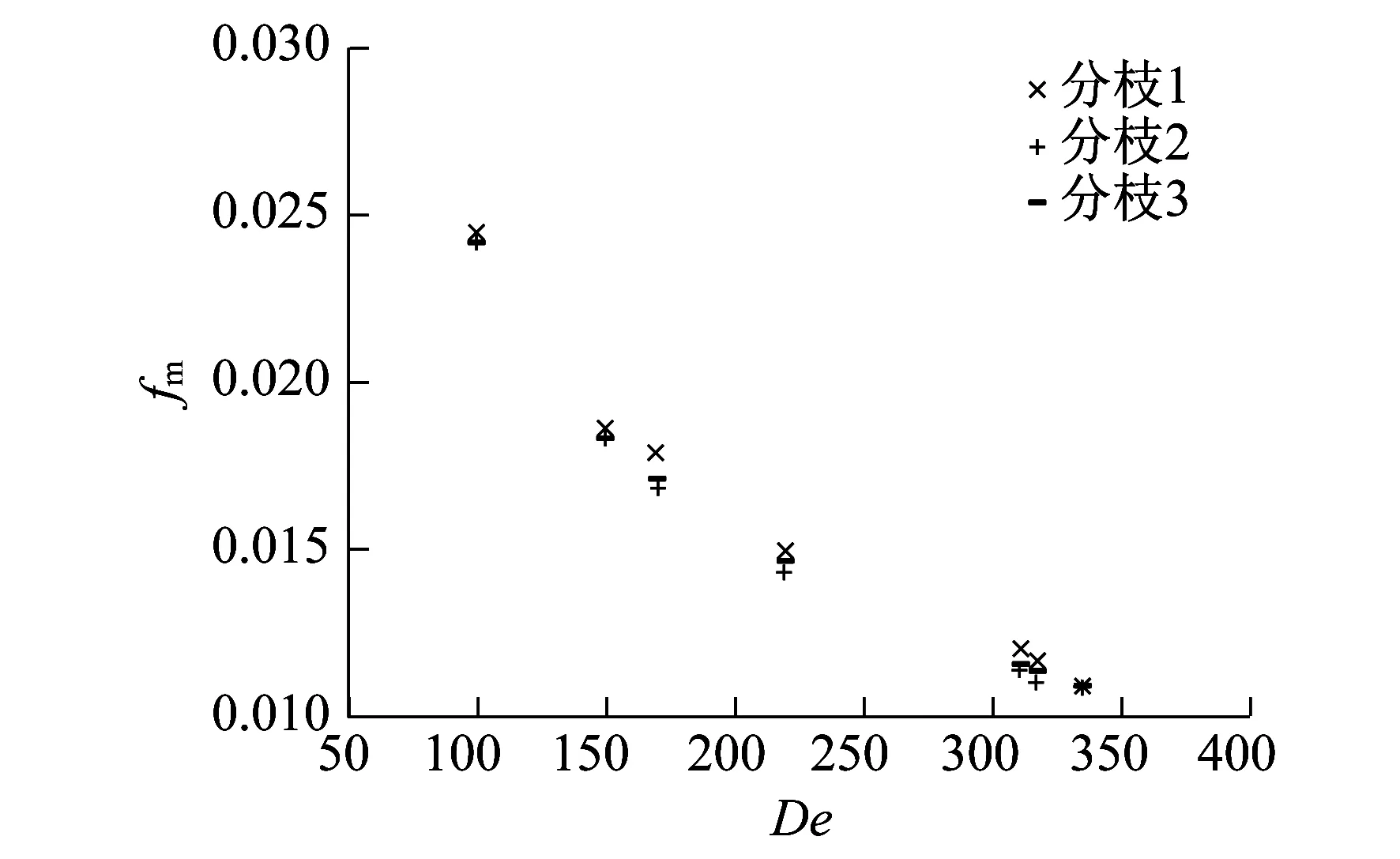
图7 弯管内球形纳米流体平均摩擦系数fm随De数的变化情况

3 结 论

运用FLUENT软件,完成对方形弯管层流范围内血小板形和球形纳米流体的数值模拟计算,得到了弯管内血小板形和球形的非线性特性。结论如下:

(1) 随着De数的变化,血小板形和球形纳米流体都存在3种不同的解分枝结构。

(2) 血小板形和球形纳米流体在7个不同的De数下存在分枝结构,并且在同一De数下,血小板形纳米流体的平均努塞尔数和平均摩擦系数均高于球形纳米流体。

(3) 弯管出口截面外壁面的局部努塞尔数和摩擦系数基本呈对称分布,沿外壁方向,外壁中心处的局部努塞尔数和局部摩擦系数较低。

参考文献：

[1] JOSEPH B,SMITH E P,ADLER R J.Numerical treatment of laminar flow in helically coiled tubes of square cross section.Part I.Stationary helically coiled tubes[J].Journal,1975,21:965-974.

[2] WINTERS K H.A bifurcation study of laminar flow in a curved tube of rectangular cross-section[J].Journal of Fluid Mechanics,1987,180:343-369.

[3] LUO W J.Flow bifurcations in a square curved tube for small curvature ratio[J].Transaction of the Aeronautical and Astronautical Society of the Republic of China,2004,36(2):163-170.

[4] 张昆,杨茉.紧致方法对流动换热及静态分岔的模拟[J].工程热物理学报,2012,33(1):109-112.

[5] 郑建城,杨茉,黄夫泉,等.封闭圆内开缝圆自然对流的非线性特性研究[J].工程热物理学报,2012,33(2):308-310.

[6] LIU F,WANG L.Analysis on multiplicity and stability of convective heat transfer in tightly curved rectangular ducts[J].International Journal of Heat & Mass Transfer,2009,52(25):5849-5866.

[7] 薛雷.方形截面弯管内的二次流动及其分叉[J].厦门理工学院学报,2013,21(1):55-59.

[8] LIU F,CAI Y,WANG L,et al.Effects of nanoparticle shapes on laminar forced convective heat transfer in curved ducts using two-phase model[J].International Journal of Heat & Mass Transfer,2018,116:292-305.