流体横掠圆柱体传热特性数值模拟的流态模型选择

,

(上海电力学院 能源与机械工程学院,上海 200090)

流体横掠圆柱体是工程中换热器最常见的流动工况。长期以来,国内外的科学家和工程技术人员对此流动工况进行了大量的研究,研究手段有试验和数值模拟两种。由于试验的条件常会受到限制,因此随着计算机的发展,自20世纪80年代以来,数值模拟成为常用的研究手段。

流体横掠圆柱体的工况极其复杂,涵盖了层流、紊流、旋涡脱落、宏观流体掺混动量交换及复杂的列结构等。通常认为,横掠圆柱体的流态主要由来流雷诺数(Re)决定。在非常低的Re下,圆柱尾部会出现不脱落的附着涡;随着Re增大,附着涡脱落,形成周期性层流涡街;当Re继续增大,流态会发生转捩,分别从远尾迹区、近尾迹区和圆柱面上开始转捩为湍流。

国内外学者对流体横掠圆柱体做了许多试验研究,分别得出不同Re下圆柱扰流的流动特征和旋涡的斯特罗哈数(St)、柱体阻力系数(Cd)以及分离角的位置等[1-8]。

采用直接模拟、大涡模拟和雷诺时均模拟等方法对亚临界雷诺数范围内的圆柱扰流进行了数值模拟,得到了各雷诺数下圆柱后的尾流流动特性[9-19]。

在紊流工况下,数值模拟的难度大大增加,现有的处理紊流的数学方法均存在各种各样的限制,还不能很好地模拟流体横掠圆柱体的所有紊流工况。采用层流方法可以大大降低计算难度和计算量,然而数值计算中的流态选择和临界雷诺数还未有明确的标准。可以确定的是,临界雷诺数不应是2 300,这是用来判断紊流的雷诺数值。根据边界层理论,边界层外流体可作为层流处理。在边界层内,从前缘点开始计算,沿流动方向长度为特征长度的雷诺数大于100 000时,边界层内的流动为紊流[20]。

对于传热方面而言,工程上更加注重平均换热的情况,所以有学者用试验关联式的方式对不同Re下的换热情况进行了总结[21-23]。

本文运用计算机流体软件,分别用层流模型、RNGk-ε紊流模型、标准k-ε紊流模型对亚临界雷诺数下的流体横掠圆柱体进行了数值模拟,计算得出了3种流态模型下不同雷诺数时的平均努塞尔数,并与试验数据进行了对比,得出了不同雷诺数工况下,流体横掠圆柱体数值模拟传热特性的流态模型选择。

1 流体横掠圆柱体工况模型的建立

1.1 物理模型

本文的研究对象是内部有一圆柱的矩形通道中的流体(空气)。圆柱的直径为D,圆柱距离流体入口15D,距离出口50D,距离上下边界面均为20D,具体如图1所示。

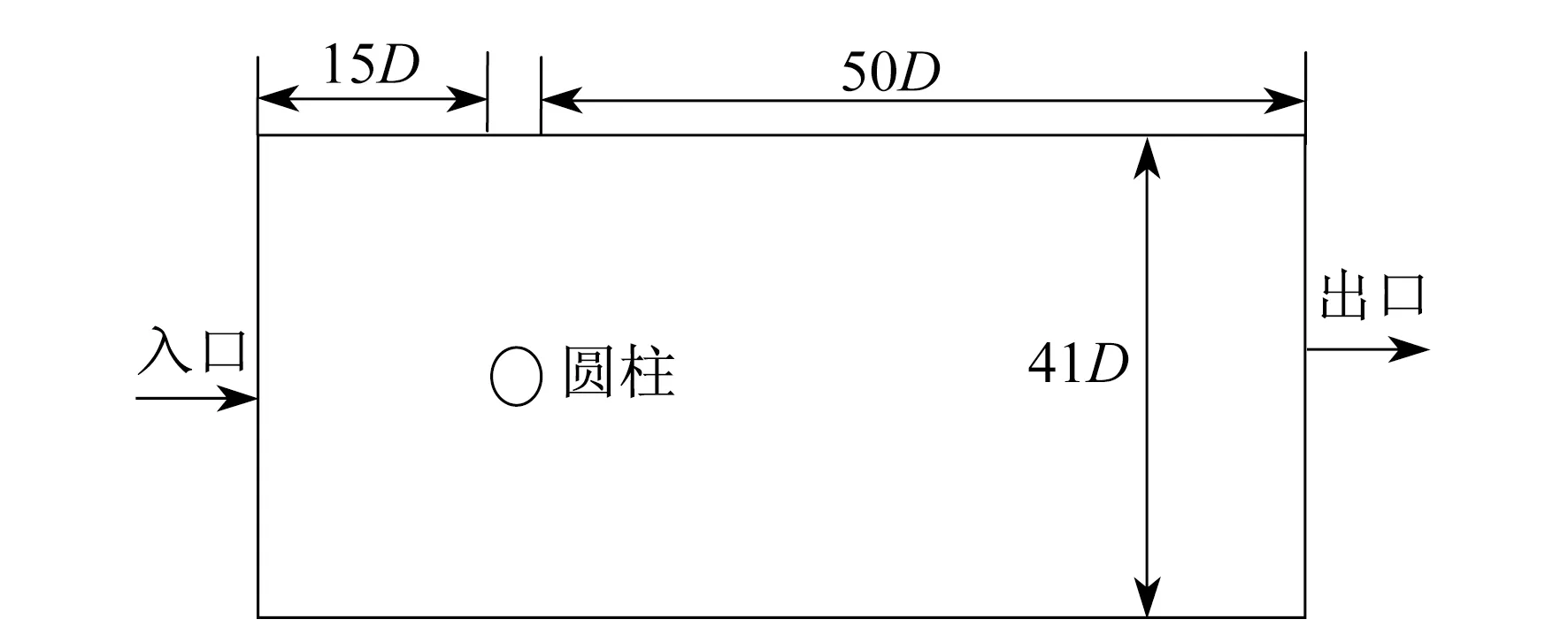
图1 流体横掠圆柱示意

通道入口的来流均匀,圆柱表面为定热流密度,冷流体对其进行冷却(即第二类热边界条件)。

1.2 相关假设

为了简化模型和减小计算量,做出以下假设:流体为不可压缩流体;忽略重力影响;物理量在管轴方向上的变量忽略不计(即简化为二维模型);所有界面和接触表面不变形,流-固接触面为无滑移边界。

1.3 数学模型

连续性方程为

(1)

式中:ρ——流体密度;

t——流动时间;

u,v——x方向和y方向的速度分量,m/s。

动量方程为[24]

(2)

式中:pxx,pyx,pxy,pyy——流体内部内应力张量分量;

Fx,Fy——单位质量力分别在x方向和y方向的分量。

能量方程为

ρdivuf+div(λgradT)+Φ+Sh

ρdivuf+div(λgradT)+Φ+Sh

(3)

式中:h——表面换热系数;

uf——流体粘度;

λ——流体的导热系数;

T——流体温度;

Φ——由于粘性作用,机械能转换为热能的部分;

Sh——流体的内热源。

1.4 边界条件

(1) 进口边界条件 计算区域进口边界条件选用速度进口边界条件,流体介质选取空气,温度T0=300 K。u=constant,v=0。

(2) 出口边界条件 计算区域空气出口边界条件选用压力出口边界条件,流动出口压力是大气压力,p=101 325 Pa。

(3) 圆柱面设置 圆柱面为无滑移固壁边界,壁面恒热流加热,u=v=0,圆柱壁面的热流密度qw=5 000 W/m2。

(4) 上下边界面的边界条件 计算区域上下边界面采用对称边界条件。

2 数值模拟

2.1 近壁区处理

壁面区可以分为粘性底层、过渡层和对数律层3个子层。在粘性底层区,流态几乎是层流,紊流应力作用极小,而标准k-ε模型只能用于求解处于紊流核心区的流动,不能处理壁面区的流动[25]。因此,本文采用壁面函数法。

2.2 网格划分和模拟工况

(1) 网格划分 采用二维模型进行计算。计算区域和全局网格、近壁面网格分别如图2和图3所示。流场网格使用分块结构化网格,壁面边界层网格采用20层膨胀比为1.05的边界层网格。

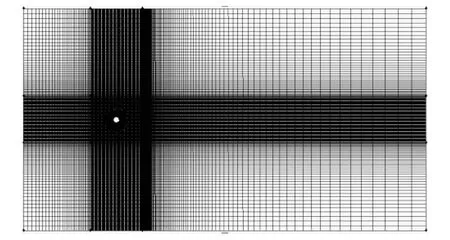
图2 计算区域和全局网格

图3 近壁面网格

(2) 模拟工况 不同Re不同模型下的时间步长如表1所示。为保证流动充分发展,每种工况均计算10 000个时间步长。为便于比较,各工况下圆柱面的热流密度均取50 000 W/m2。

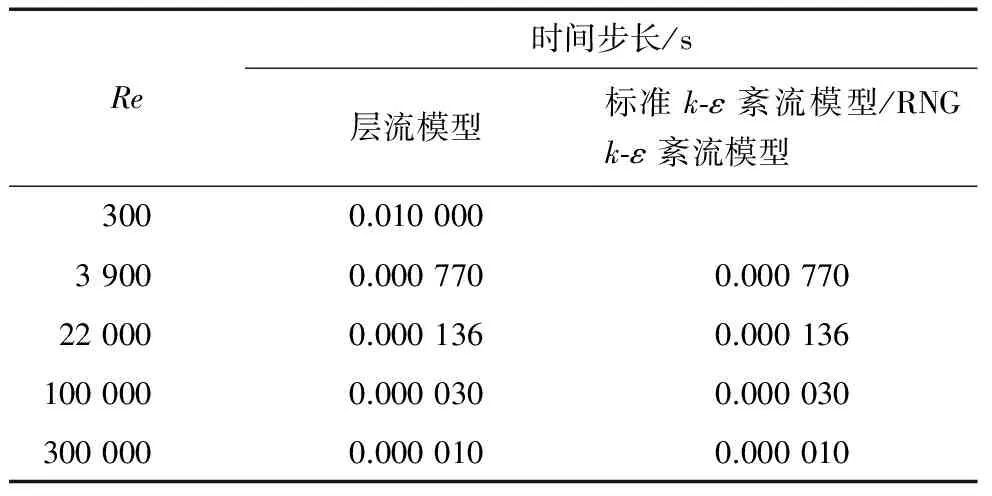
表1 不同Re不同模型下的时间步长

3 换热特性模拟结果及分析

虽然横掠圆柱体的流动局部换热系数变化非常复杂,但平均换热系数的渐变规律性很强,CHURCHILL S W和BERNSTEIN M通过试验得出了努塞尔数(Nu)的关系式[23]为

(4)

流体的定性温度为(tw+tf)/2;特征尺度选取管外径;Re计算式中的特征速度按通道来流速度计算。在低雷诺数时,主流区和边界层的流体均为层流,因此对Re=300的工况,只采用层流模型计算。在高雷诺数时,分别采用两种紊流模型计算。表2为模拟计算得出的圆柱壁面的平均Nu。

由表2可以看出,当Re大于3 900时,采用紊流计算与试验值更接近;当Re为3 900～22 000时,采用标准k-ε紊流模型更合适;当Re为100 000～300 000时,采用RNGk-ε紊流模型更合适。当Re为3 900时,用流体分子脉动模型已不能反映热交换的本质。需要注意的是,不同紊流模型下,计算结果有较大差异,这与紊流模型建立时的假设条件有关。这一问题仍在研究中。

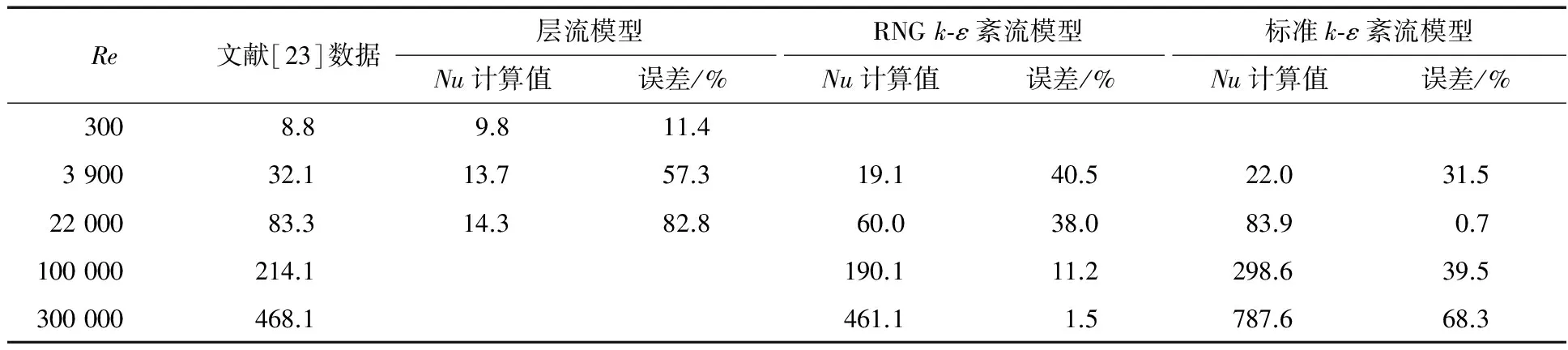
表2 平均努塞尔数Nu模拟计算结果

4 结 论

(1) 当Re≤3 900时,采用层流模型较合适,误差为11.4%～57.3%。在此范围内,Re越小则误差越小。

(2) 当3 900≤Re≤22 000时,采用标准k-ε紊流模型较合适,误差为0.7%～31.5%。在此范围内,Re越大则误差越小。

(3) 当22 000≤Re≤300 000时,采用RNGk-ε紊流模型较合适,误差为1.5%～38.0%。在此范围内,Re越大则误差越小。

参考文献：

[1] WHITE F M.Viscous fluid flow[M].New York:McGraw-Hill Inc.,1974:76-81.

[2] ZDRAVKOVICH M M.Flow around circular cylinders,Vol.I:Fundamental[M].New York:Oxford University Press,1997:201-213.

[3] ONG L,WALLACE J.The velocity field of the turbulent very near wake of a circular cylinder[R].Washington DC:NASA TM 110513,1995.

[4] JONES G W,CINCOTTA J,WALKER W.Aerodynamic forces on a stationary and oscillating circular cylinder at high Reynolds numbers[R].Washington DC:NASA TR R-300,1969.

[5] SON J,HANRATTY T J.Velocity gradients at the wall for flow around a cylinder at Reynolds numbers 5×103to 105[J].Journal Fluid Mechanics,1969,35:353.

[6] NIEMANN H J,HOLSCHER N.A review of recent experiments on the flow past circular cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics,1990,33(1):197-209.

[7] ACHENBACH E.Distribution of local pressure and skin friction around a circular cylinder in cross-flow up toRe=5×106[J].Journal of Fluid Mechanics,1968,34(4):625-639.

[8] 史里希廷 H.边界层理论[M].徐燕侯,译.北京:科学出版社,1988:62-66.

[9] 李兆辉,张剑飞,陶文铨.DES湍流模型计算Re=3 900的圆柱扰流[J].工程热物理学报,2013,34(9):1703-1706.

[10] 陈禹,李强,郭廷凯.不同雷诺数下的圆柱绕流数值模拟研究[J].中国水运(下半月),2015,15(7):88-90.

[11] 张群峰,何鸿涛,吕志咏.二维圆柱层流绕流及其控制数值模拟[J].科学技术与工程,2009,9(5):1187-1193.

[12] 赵萌,毛军,郗艳红.高雷诺数下有限长圆柱绕流阻力特性研究[J].机械工程学报,2015,51(22):176-182.

[13] 沈立龙,刘明维,吴林键,等.亚临界雷诺数下圆柱和方柱绕流数值模拟[J].水道港口,2014,35(3):227-233.

[14] 张群峰,何鸿涛.不同湍流模型数值模拟三维轴对称凸体分离流动的比较[J].科学技术与工程,2009,9(13):3693-3697.

[15] 翟明,董芃,王希影,等.圆管湍流脉动流动与换热的数值模拟[J].中国电机工程学报,2009,29(20):85-91.

[16] 潘维,池作和,斯东波,等.匀速流体横掠管束的流场数值模拟[J].浙江大学学报(工学版),2004(8):110-113.

[17] 季魁玉,费昕阳,周子杰,等.带扰流圆柱肋楔形通道的流动与换热数值研究[J].燃气轮机技术,2016,29(1):36-40.

[18] 曹丰产,项海帆.圆柱非定常绕流及涡激振动的数值计算[J].水动力学研究与进展(A辑),2001,16(1):111-118.

[19] 詹吴,李万平,方秦汉,等.不同雷诺数下圆柱绕流仿真计算[J].武汉理工大学学报,2008(12):33-35.

[20] 孔珑.工程流体力学[M].北京:中国电力出版社,2006:18-110.

[21] 杨世铭.传热学[M].4版.北京:高等教育出版社,2006:389-403.

[22] 杨春.不同边界条件下园管对流换热系数的研究[D].重庆:重庆大学,2006.

[23] CHURCHILL S W,BERNSTEIN M.A correlating equation for forced convection from gases and liquids to a circular cylinderincrossflow[J].ASMEJ Heat Transfer,1997,99(1):300-306.

[24] 张鸣远.高等流体力学[M].西安:西安交通大学出版社,2006:56-57.

[25] 冯沧.泵站前池进水流态数据模拟研究[D].上海:同济大学,2001.