纳米颗粒形状对螺旋管强化传热的影响

, ,

(上海电力学院 能源与机械工程学院,上海 200090)

换热装置的高效强化传热问题一直备受关注,将螺旋管设备与纳米流体工质相结合的强化传热技术已经得到广泛研究及应用。目前,螺旋管强化传热的研究主要集中于探讨螺旋管尺寸、雷诺数大小、纳米流体浓度、颗粒粒径对其传热性能的影响[1-3]。过去的研究主要分析球形纳米流体在螺旋管内的传热特性,而对非球形颗粒(如棒状形、砖形、刀片形等)纳米流体在螺旋管内传热性能的研究较少。颗粒形状对纳米流体的导热系数和粘度存在不同的影响[4-5],同样对纳米流体传热性能的影响也不同,因此研究纳米颗粒形状对螺旋管传热特性的影响具有重要的意义。

HWANG K S等人[6]实验研究了不同形状的Al2O3-水纳米流体在圆管内的对流换热特性,结果表明,不同形状纳米流体的压降随纳米颗粒尺寸的增大而降低;纳米流体传热强度与颗粒形状、尺寸有关。FERROUILLAT S等人[7]实验研究了球形、香蕉形SiO2-水纳米流体和多边形、棒状形ZnO-水纳米流体在水平圆管内冷却或加热的传热特性,结果表明,香蕉形、棒状形纳米流体的压降分别低于球形、多边形的压降,而多边形氧化锌纳米流体的传热强度大于棒状形。VANAKI S M等人[8]采用单相流法模拟了不同形状SiO2-EG纳米流体在波壁管内的热传递特性,结果表明,血小板形状纳米流体的强化传热强度最高。YU L等人[9]实验研究了球形和非球形Al2O3-PAO纳米流体在圆管内的对流换热,结果表明,在相同体积浓度下,非球形纳米流体的传热强度大于球形纳米流体;非球形纳米流体的压降高于球形纳米流体的压降。

目前对不同颗粒形状纳米流体强化换热的研究主要是采用实验和单相流模拟的方法,单相流法是将纳米流体视为单一的均匀流体,需要通过理论公式来求解纳米流体的物性参数。本文采用欧拉-拉格朗日两相流的方法模拟螺旋管内不同颗粒形状Al2O3-水纳米流体的传热性能,在两相流法中,直接设置颗粒和基液的物性参数,考虑颗粒球形度和近似球形粒径的因素,分析不同颗粒形状对螺旋管传热性能的影响。

1 数值模型

1.1 物理模型

图1为螺旋管的物理模型,螺旋直径D为120 mm,螺距P为30 mm,螺旋圈数8圈,管径d为10 mm。螺旋管入口温度设定为293.15 K,入口速度的大小随雷诺数Re的变化而变化(Re范围为750～1 750),采用速度入口和压力出口边界条件;采用定热流密度的壁面条件,热流量为5 000 W/m2,壁面无滑移。

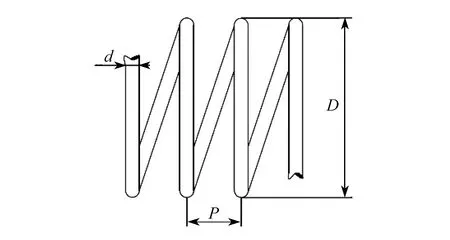
图1 螺旋管物理模型

1.2 控制方程

采用离散相模型进行数值模拟。将纳米流体视为液体相和颗粒相,液体相处理为连续介质,考虑两相间的相互作用力,作用力中考虑颗粒球形度和近似球形粒径。模拟过程中假设:管内流动为稳态层流;流体为不可压缩流体;流体物性参数为常数。那么,螺旋管内流动和传热的控制方程如下。

液体相质量方程为

(1)

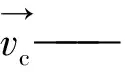
液体相动量方程为

ρcp+

(2)

(3)

式中:ρc——液体密度;

g——重力加速度;

μc——液体粘度;

Sm——动量源相;

δV——单元体内颗粒的数量;

mp——颗粒质量;

液体相能量方程为

ρc(λcTc)+Sh

(4)

(5)

式中:cpc——液体比热容;

Tc——液体温度;

λc——液体导热系数;

Sh——能量源相;

hcp——颗粒表面传热系数;

dp——颗粒粒径;

Tp——颗粒温度。

在拉格朗日坐标下,颗粒相中单位颗粒质量下的运动方程为

(6)

(7)

(8)

(9)

式中:ρp——颗粒密度;

μ——动力粘度;

CD——阻力系数;

Recp——相对雷诺数;

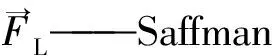
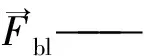
当颗粒形状为球形时,则CD的表达式[10]为

(10)

其中,a1,a2,a3是常数,根据Recp的范围来取值,由于纳米颗粒粒径比较小,即Recp<<1,则a1=a3=0,a2=24。

当颗粒形状为非球形时,则CD的表达式[11]为

(11)

其中,

b1=exp(2.328 8-6.458 1φ+2.448 6φ2)

(12)

b2=0.096 4+0.556 5φ

(13)

b3=exp(4.905-13.894 4φ+18.422 2φ2-

10.259 9φ3)

(14)

b4=exp(1.468 1+12.258 4φ-20.732 2φ2+

15.885 5φ3)

(15)

式中:Resph——与颗粒具有相同体积的球形的雷诺数;

φ——颗粒的球形度。

文献[11]中非球形的CD值是通过将球形度在0.123～0.906之间的实验数据值与理论值进行比较验证所得到的,两者误差在4.9%以内,吻合较好。本文的球形度在0.36～0.81之间,因此满足文献[11]中CD计算公式的球形度要求。

颗粒相的能量方程为

(16)

式中:cpp——颗粒比热容;

Ap——颗粒表面积。

颗粒表面传热系数hcp的计算公式为

(17)

式中:Rep——颗粒雷诺数;

Pr——普朗特数。

1.3 数值方法

本文选用5种不同形状的勃姆石(Al2O3)纳米颗粒,分别为血小板形、圆柱形、刀片形、砖形、球形,其形状如图2所示。采用有限体积的离散方法求解以上氧化铝纳米颗粒的质量、动量、能量等控制方程;压力和速度求解采用压力耦合方程的SIMPLE算法;对流项和扩散相采用二价迎风格式。

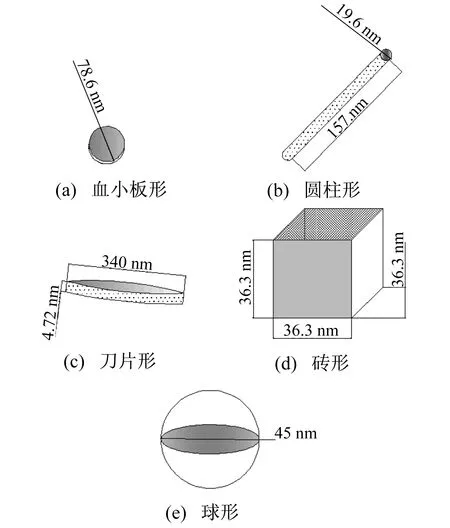
图2 氧化铝纳米颗粒形状

液体相选用纯水,纳米颗粒和水的物性参数如表1所示。纳米颗粒的形状尺寸如表2所示[12]。

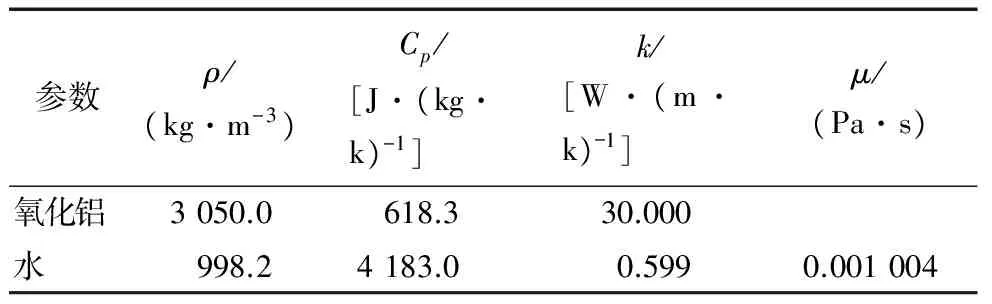
表1 氧化铝和水的物性参数

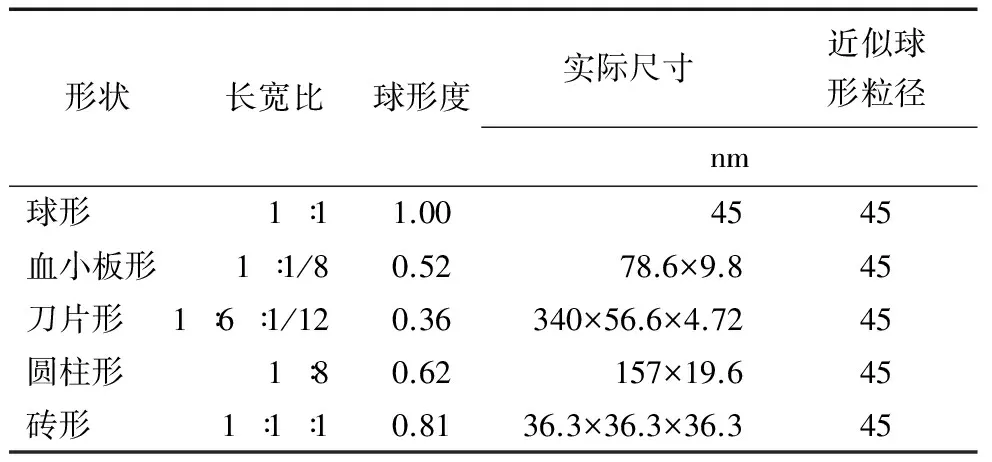
表2 纳米颗粒形状及尺寸

1.4 网格无关性验证

采用结构化网格对计算域进行网格划分,设置了180万到477万个不同的网格数对体积浓度为1%的圆柱形纳米流体进行对流换热模拟。结果表明:努塞尔数Nu随网格数的增加而增大,其中网格数为3 420 684时,Nu=20.68;网格数为4 778 676时,Nu=20.71,两者相差0.15%,考虑到计算精度和计算机性能,故最终采用3 420 684个的网格数进行模拟计算。

1.5 模型验证

本文采用文献[13]中螺旋管内球形TiO2-水纳米流体对流传热的实验结果对以上的数值方法进行验证。模拟与实验结果如图3(a)所示。由图3(a)可知:当Re分别为在560,700,1 250时,模拟结果与文献中的实验数据吻合较好,误差在6%之内;当Re分别为1 750,2 750,3 400时,模拟结果低于文献中的实验结果,但误差在8.7%之内。

另外,本文还将以上的数值方法对文献[9]中的棒状形Al2O3-PAO纳米流体在圆形管内的对流换热进行了验证,结果如图3(b)所示,数值模拟结果与文献中实验数据吻合较好,误差在6%之内。

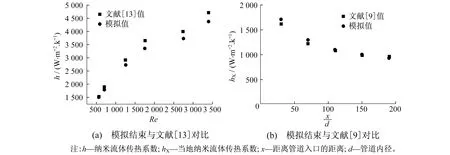
图3 模拟结果与参考文献中实验结果对比

2 结果与讨论

本文主要分析5种不同纳米颗粒形状对螺旋管内纳米流体的努塞尔数Nu,压降和热力性能的影响。纳米颗粒形状的影响主要从两方面考虑:一是颗粒的球形度和近似球形粒径;二是颗粒形状对纳米流体的粘度、导热系数的影响也不同,与颗粒形状有着复杂的关系。因此,本文引用文献[12,14]中不同纳米颗粒形状的导热系数、粘度系数的理论公式进行计算,比较分析在近似球形粒径相同条件下,不同颗粒形状对螺旋管内纳米流体传热性能的影响情况。

压降为相应管段内进口静压与出口静压之差;而Nu的计算公式为

(18)

式中:hnf——纳米流体传热系数;

λnf——纳米流体有效导热系数。

球形纳米流体有效导热系数[13]为

(19)

式中:λp——颗粒导热系数;

φ——颗粒体积浓度。

球形纳米流体有效粘度[13]为

(20)

式中:μnf——纳米流体有效粘度;

μC——液体水的粘度。

本文设定不同形状纳米颗粒的近似球形粒径相同,则纳米流体的有效导热系数采用Hamilton-Crosser模型[14]进行计算:

(21)

式中:n——形状因子。

对于非球形纳米流体有效粘度的计算,采用文献[12]中非球形纳米流体粘度系数的经验公式。因为纳米流体的有效粘度在一定的体积浓度下,其颗粒体积浓度的影响比粒径的影响更为明显,文献[15]中得出纳米颗粒体积浓度小于4%时,不同粒径Al2O3氧化铝-水纳米流体的粘度系数大致相同。本文模拟的纳米颗粒体积浓度为0.5%～2%,因此引用非球形纳米流体有效粘度系数[12]的公式为

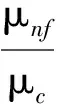
(22)

其中A1和A2的值如表3所示。

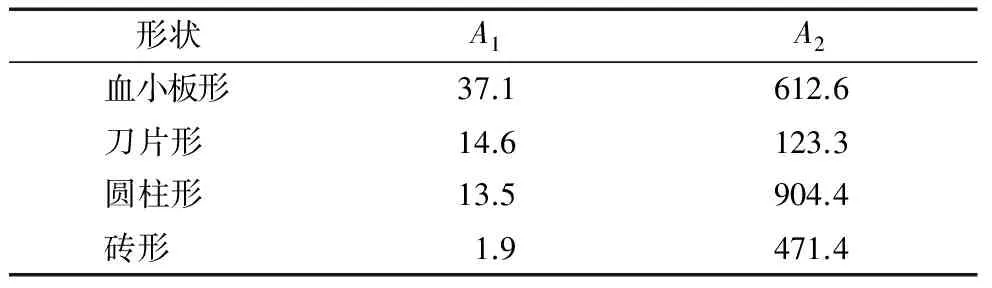
表3 不同形状纳米流体的A1和A2的值

摩擦系数[13]为

(23)

式中:ΔP——压降;

L——管道周长;

ρ——流体密度;

v——流体速度。

2.1 不同颗粒形状对螺旋管入口段的传热影响

当Re为1 000,体积浓度为1%时,不同颗粒形状的努塞尔数Nu和摩擦系数f沿管长方向的变化如图4所示。其中,θ为相对于入口截面的旋转角度。从图4(a)可以看出,Nu在螺旋管入口段内出现振荡,振荡幅度沿管长的增加而减小,最后,这种振荡随着纳米流体的流动进入充分发展段而受到抑制。这是由于沿螺旋管方向,管内流体高流速区域的振荡引起Nu的波动。该模拟结果与文献[2]中研究的结果一致。从图4(b)可以看出,不同颗粒形状纳米流体和纯水的摩擦系数均在入口段内出现振荡,而在θ为360°之后摩擦系数波动减小,摩擦系数基本恒定。

2.2 不同颗粒形状对螺旋管充分发展段的传热影响

2.2.1 体积浓度

图5模拟了体积浓度φ为0.5%～2%的Al2O3-水纳米流体在Re=1 000时的对流传热情况。从图5(a)可以看出,随着体积浓度的增加,充分发展段内纳米流体的平均努塞尔数Num均增大。其中,血小板的传热强度增幅最大,其在体积浓度为2%时比纯水提高了27.2%,这与血小板的尺寸(78.6 nm×9.8 nm)有关。在体积浓度一定的情况下,小尺寸颗粒间的扩散和相对运动将热量迅速传递给流体,从而强化了换热。其他形状的传热能力依次降低的顺序为圆柱形、刀片形、球形、砖形。图5(b)中,随颗粒体积浓度的增大,不同形状纳米流体的压降均增大。其中,血小板形的压降增幅最大,在体积浓度为2%时比纯水的压降增加了73.7%,其他形状的压降增幅依次降低的顺序为圆柱形、刀片形、球形、砖形。

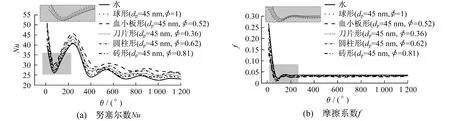
图4 不同颗粒形状纳米流体的努塞尔数和摩擦系数沿管长方向的变化

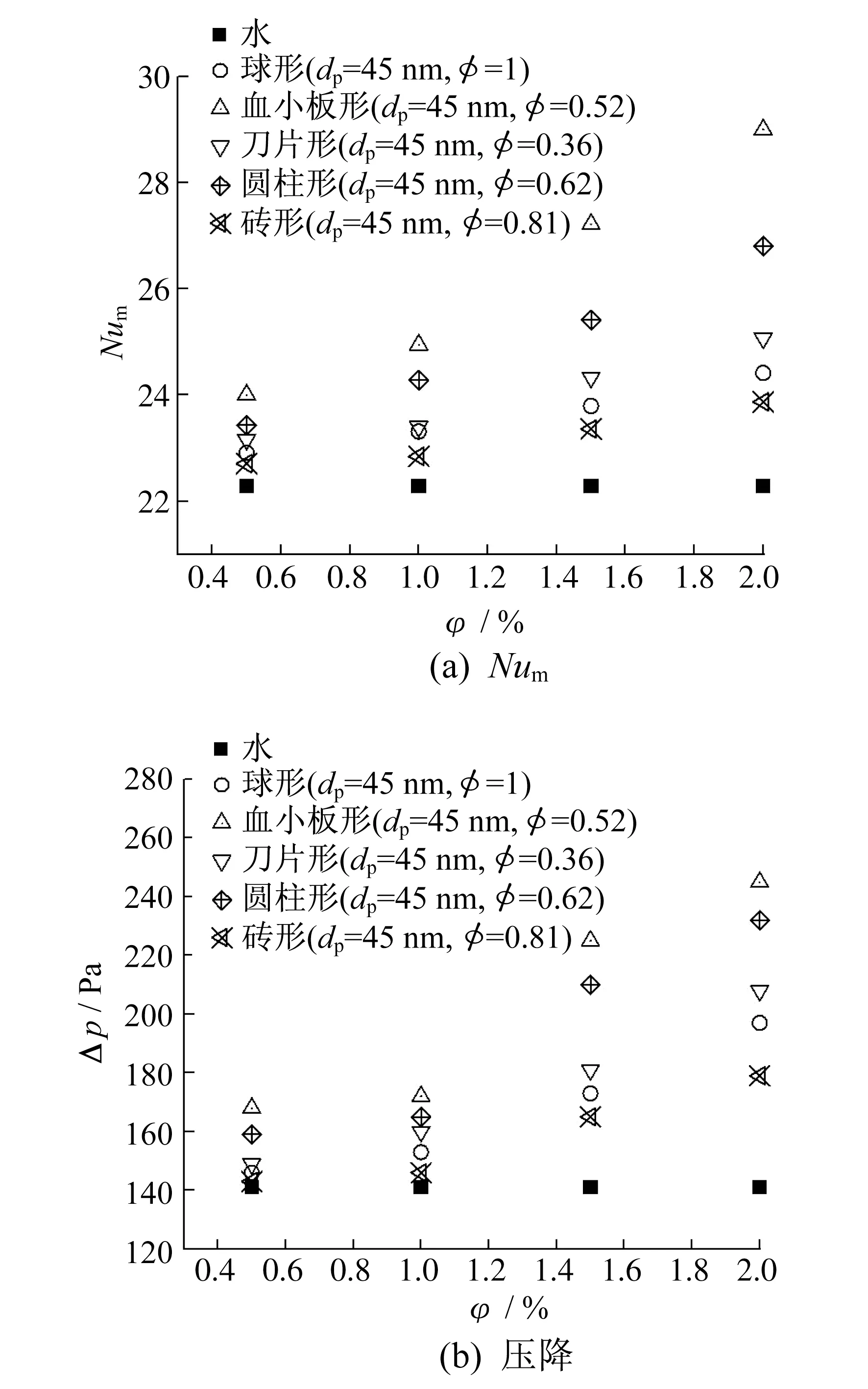
图5 不同颗粒形状纳米流体Num和压降随体积浓度的变化

2.2.2 颗粒形状及尺寸

当Re为1 000,体积浓度为1%时,颗粒形状及尺寸对传热性能的影响如图6所示。图6(a)中,在颗粒形状一定的情况下,随着粒径的增大,纳米流体的Num减小,这是由于粒径越小的颗粒在基液中的布朗运动越激烈,热量传递的速率越快,则对流强度随之增大。图6(b)中,在颗粒球形度一定时,粒径越小,压降越大。粒径越小,颗粒的布朗运动越剧烈,在管道壁面处的扰动增大引起颗粒间的动量交换增强,从而引起轴向压降增大。

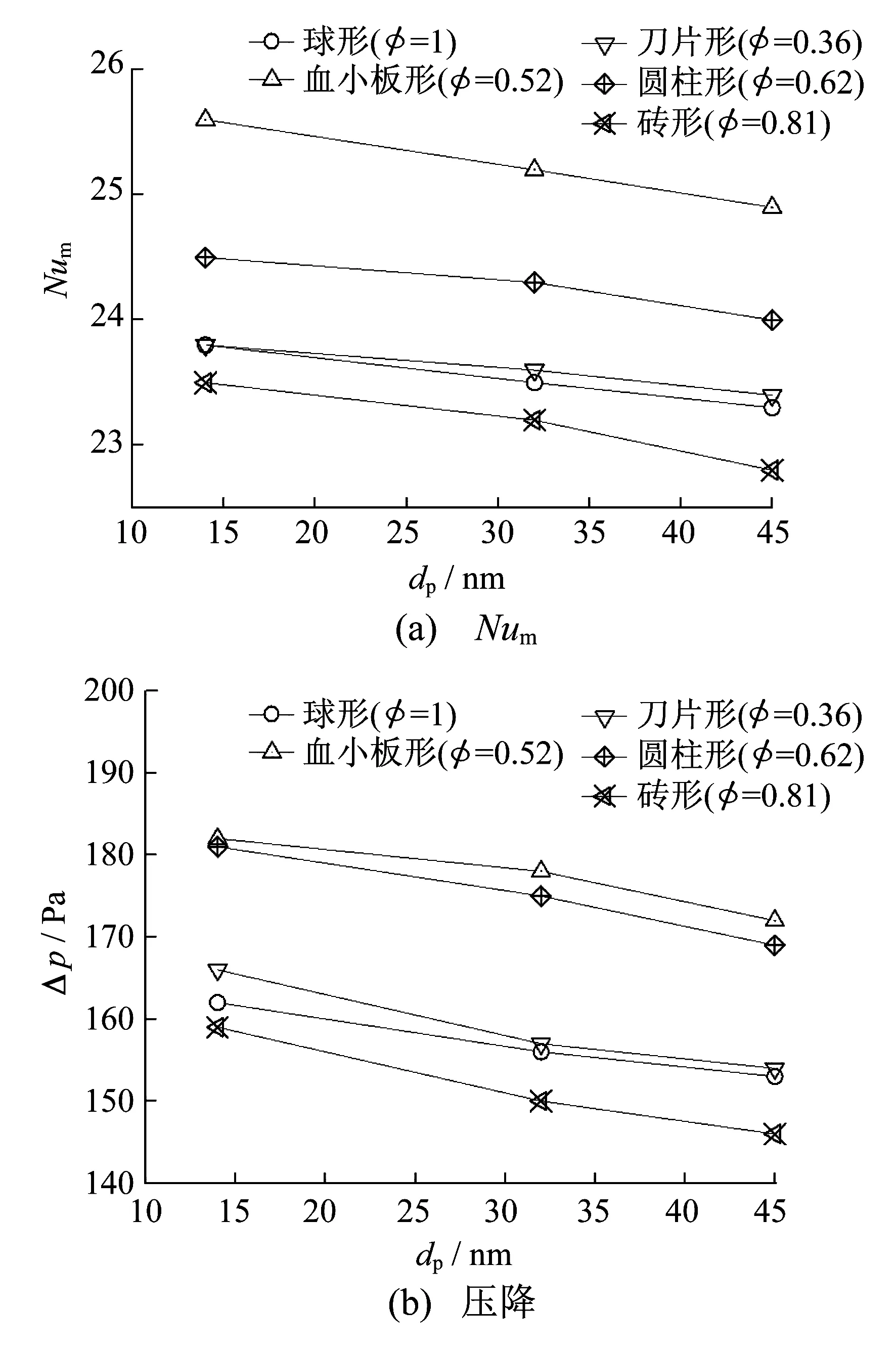
图6 不同颗粒形状纳米流体Num和压降随粒径的变化

2.2.3 雷诺数

当体积浓度为1%时,不同雷诺数下颗粒形状对螺旋管传热性能的影响如图7所示。图7(a)中,随着Re增加,不同形状纳米流体的平均努塞尔数Num均增大。在Re=1 750时,血小板形、圆柱形、刀片形、球形、砖形比纯水的Nu分别数提高了16.6%,10.4%,7.3%,5.1%,4.0%。根据模拟结果,采用MATLAB多元回归法拟合Num数随雷诺数Re,球形度φ,普朗特数Pr,体积浓度φ的变化关系,拟合公式为

Num=0.4364Re0.370 3Pr0.406 2φ0.067 2(2.491+

0.131φ-0.085 7φ2)

(24)

拟合相关系数为96.61%。

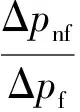
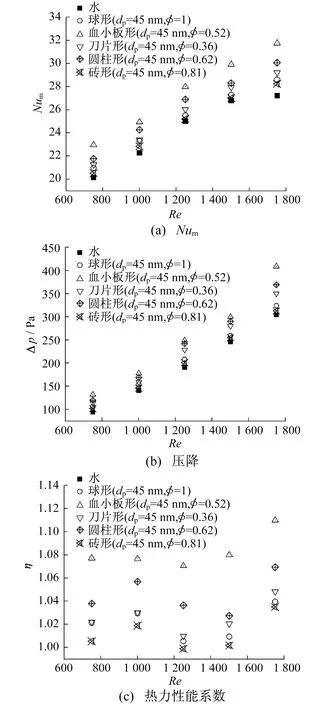
图7 不同颗粒形状纳米流体Num和压降及热力性能系数随Re的变化

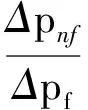
3.136φ-3.23φ2)

(25)

拟合相关数为90.46%。

颗粒形状对螺旋管内的传热和压降同时存在影响,对此,引用热力性能系数对传热和压降的共同作用进行评价。纳米流体的热力性能系数[16]定义为

(26)

式中:Nunf,Nuf——纳米流体和纯水的努塞尔数。

从图7(c)可以看出,血小板形纳米流体的传热性能高于其他形状,且在Re=1 750时,热力性能系数η达到最大值1.11;其他形状的强化传热性能依次降低的顺序为:圆柱形、刀片形、球形、砖形。

2.2.4 颗粒浓度分布

当体积浓度为1%,Re为1 000时,不同颗粒形状纳米流体螺旋管出口截面上的颗粒浓度图、速度图和温度图如图8和图9所示。从图8可以看出,纳米颗粒浓度在管内的分布是不均匀的,由于受到离心力的作用,不同形状纳米流体的颗粒浓度分布均呈旋涡状,旋涡中心处的颗粒浓度分布较低,而流体核心区和靠近壁面处的颗粒浓度相对较高。从图9可以看出,在管道壁面处,由于牛顿内摩擦力的影响使得流体在靠近壁面处的速度减小,而颗粒在此处的浓度相对较大,由于颗粒导热系数较大,能够迅速将热量从高温区传向低温区,使得此处的温度分布较高。

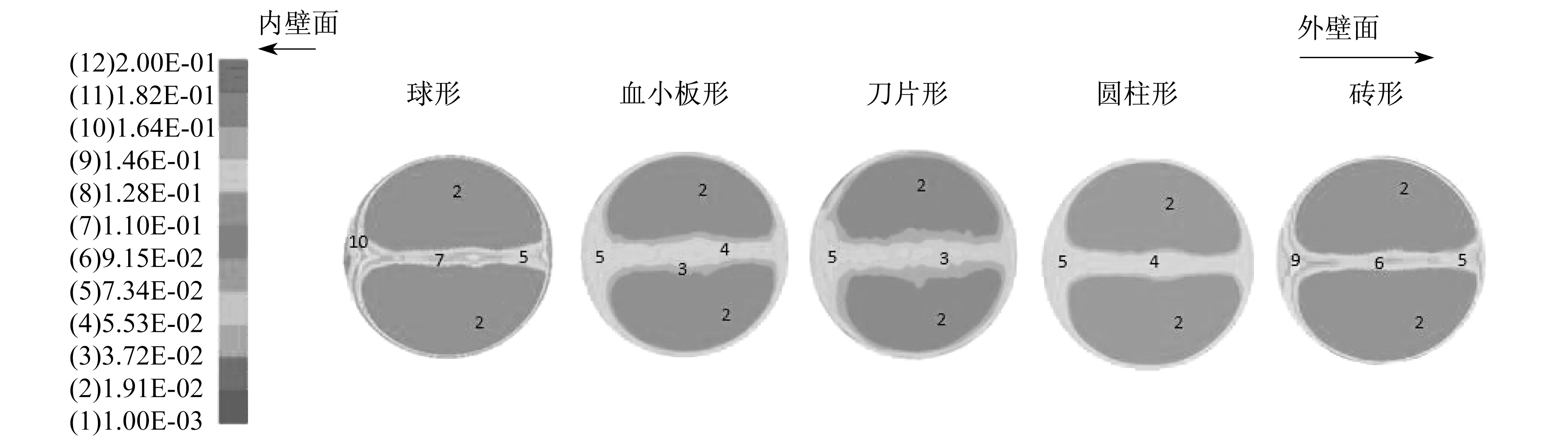
图8 不同颗粒形状纳米流体出口截面上的颗粒浓度分布

图9 不同颗粒形状纳米流体出口截面上的速度和温度分布

在颗粒浓度分布较低的旋涡中心区域,温度分布也较低,这是因为颗粒分布少的区域热量传递速率减慢。

3 结 论

(1) 在螺旋管入口段内,不同形状纳米流体的努塞尔数、摩擦系数出现振荡,振荡幅度随管长的增大而减小,并随流动进入充分发展段而受到抑制。

(2) 随着体积浓度的增加,纳米流体的平均努塞尔数和压降均增大;不同形状纳米流体的平均努塞尔数和压降增幅由高到低的顺序为血小板形、圆柱形、刀片形、球形、砖形。

(3) 在颗粒形状一定的情况下,粒径越小,传热强度越大,压降也越大。

(4) 随着雷诺数的增加,纳米流体的传热强度和压降均增大;不同形状纳米流体的传热强度和压降由高到低的顺序为血小板形、圆柱形、刀片形、球形、砖形。血小板形的热力性能优于其他形状,在Re=1 750时,热力性能系数η达到最大值1.11。

(5) 颗粒浓度的分布与温度、速度分布相关,在颗粒浓度分布较高的壁面处,流体速度较低而温度较高;在颗粒浓度分布较低的区域,流体温度分布较低。

参考文献：

[1] RAKHSHA M,AKBARIDOUST F,ABBASSI A,et al.Experimental and numerical investigations of turbulent forced convection flow of nano-fluid in helical coiled tubes at constant surface temperature[J].Powder Technology,2015,283(4):178-189.

[2] MIRFENDERESKI S,ABBASSI A,SAFFAR-AWAL M.Experimental and numerical investigation of nanofluid heat transfer in helically coiled tubes at constant wall heat flux[J].Advanced Powder Technology,2015,26(5):1483-1494.

[3] KUMAR P C M,KUMAR J,TAMILARASAN R,et al.Heat transfer enhancement and pressure drop analysis in a helically coiled tube using Al2O3/water nanofluid[J].Journal of Mechanical Science and Technology,2014,28(5):1841-1847.

[4] KIM H J,LEE S H,LEE J H,et al.Effect of particle shape on suspension stability and thermal conductivities of water-based bohemite alumina nanofluids[J].Energy,2015,90(S1):1290-1297.

[5] JEONG J,LI C G,KWON Y H,et al.Particle shape effect on the viscosity and thermal conductivity of ZnO nanofluids[J].International Journal of Refrigeration,2013,36(8):2233-2241.

[6] HWAMG K S,HA H J,LEE S H,et al.Flow and convective heat transfer characteristics of nanofluids with various shapes of alumina nanoparticles[C]//ASME 2009 Second International Conference on Micro/Nanoscale Heat and Mass Transfer,2010:455-460.

[7] FERROUILLAT S,BONTEMPS A,PONCELET O,et al.Influence of nanoparticle shape factor on convective heat transfer and energetic performance of water-based SiO2and ZnO nanofluids[J].Applied Thermal Engineering,2013,51(S1-2):839-851.

[8] VANAKI S M,MOHAMMED H A,ABDOLLAHI A,et al.Effect of nanoparticle shapes on the heat transfer enhancement in a wavy channel with different phase shifts[J].Journal of Molecular Liquids,2014,196(8):32-42.

[9] YU L,LIU D,BOTZ F.Laminar convective heat transfer of alumina-polyalphaolefin nanofluids containing spherical and non-spherical nanoparticles[J].Experimental Thermal & Fluid Science,2011,37(1):72-83.

[10] MAHDAVI M,SHARIFOUR M,MEYER J P.CFD modelling of heat transfer and pressure drops for nanofluids through vertical tubes in laminar flow by Lagrangian and Eulerian approaches[J].International Journal of Heat & Mass Transfer,2015,88:803-813.

[11] HAIDER A,LEVENSPIEL O.Drag Coeffieient and terminal velocity of spherical and nonspherical particles[J].Power Technology,1989,58(1):63-70.

[12] TIMOFEEVA E V,ROUTBORT J L,SINGH D.Particle shape effects on thermophysical properties of alumina nanofluids[J].Journal of Applied Physics,2009,106(1):KN-11.

[13] KAHANI M,HERIS S Z,MOUSAVI S M.Experimental investigation of TiO2/water nanofluid laminar forced convective heat transfer through helical coiled tube[J].Heat and Mass Transfer,2014,50(11):1563-1573.

[14] AZMI W H,SHARMA K V,MAMAT R,et al.The enhancement of effective thermal conductivity and effective dynamic viscosity of nanofluids-A review[J].Renewable & Sustainable Energy Reviews,2016,53:1046-1058.

[15] NGUYEN C T,DESGRANGES F,ROY G,et al.Temperature and particle-size dependent viscosity data for water-based nanofluids-Hysteresis phenomenon[J].International Journal of Heat & Fluid Flow,2007,28(6):1492-1506.

[16] KAHANI M,HERIS S Z,MOUSAVI S M.Comparative study between metal oxide nanopowders on thermal characteristics of nanofluid flow through helical coils[J].Powder Technology,2013,246(9):82-92.