真空环境下C形密封圈力学性能和泄漏率的有限元分析

张伟政，席喜林，丁雪兴，李水平

(兰州理工大学石油化工学院，甘肃 兰州 730050)

辅助密封圈中用得最早、最多、最普遍的是O形密封圈(简称O形圈)[1]，虽然O形圈有许多优点，但随着工业的发展，人们对密封的要求越来越苛刻，同时受到O形圈自身的橡胶材料特性限制，O形圈已经很难满足人们对密封性能的需求。C形密封圈(简称C形圈)由俗称“塑料王”的聚四氟乙烯(PTFE)包裹弹簧制成，因而用PTFE制作的C形圈比用橡胶制作的O形圈具有更好的力学特性和润滑特性。同时，因为C形圈可以通过弹簧施加预紧力，所以C形圈比O形圈在结构上具有较好的自紧特性。目前国内外对O形圈的研究很多，但对C形圈的研究基本没有，只是对PTFE及其相关产品做了大量的研究[2-4]。国内外学者利用各种有限元软件对O形圈的力学性能进行了大量的分析研究[5-8]，得出不同工况条件下的O形圈的应力应变以及接触应力的分布规律；学者们也对O形圈进行了许多摩擦磨损方面的实验研究[9-11]，得出了不同工况对O形圈摩擦性能的影响；此外人们对O形圈的泄漏也做了一些研究[12-13]。同时，人们还对D形密封圈[14]、矩形密

封圈[15]、Y形密封圈[16]、Yx形密封圈[17]等不同形状的密封圈进行了有限元分析和结构优化。考虑到之前学者们对C形圈的研究较少，故本文对C形圈在真空环境下的力学性能和泄漏率进行有限元模拟分析。

1 C形圈密封的机理

在未受介质压力作用时，将C形圈装入密封槽中，如图1所示。由于C形圈的主材料PTFE自身的特性，通过作为C形圈骨架的弹簧产生了一定的预紧反弹力，使得整个C形圈与被密封件紧密接触，从而产生一定的接触应力。

图1 C形圈的几何模型

在介质压力作用下，C形圈外部的PTFE将会向密封槽两侧发生弹性滑移和微量蠕动，直到C形圈整个外边缘与密封腔体侧面紧密贴合，这一过程是由线接触向面接触转化的过程。同时，C形圈骨架弹簧在介质压力作用下发生变形，产生一定的反弹力。在弹簧预紧反弹力和介质压力作用所产生反弹力的共同作用下，密封面间产生大于被密封流体介质压力的接触应力，C形圈从而完成了密封的使命。

2 有限元模型的建立

本文分析所用的C形圈内径为225.4mm，宽为5.5mm，高为3.4mm。考虑到C形圈复杂的边界条件，用有限元方法分析C形圈的力学性能时，将C形圈及其密封结构的轴套、密封槽进行整体分析。根据整个密封结构的特性，本文选取C形圈密封结构的1/96作为研究对象。PTFE为大变形的非线性材料，其材料参数通常通过单轴拉伸试验来确定。弹簧材料为304不锈钢，弹性模量为193GPa。C形圈采用六面体单元，弹簧采用六面体和四面体混合单元。用HyperMesh进行网格划分，其中划分节点数为7 734，单元数为5 214。密封沟槽、轴套与C形圈主材料PTFE的接触定义为rigid-deformable，即定义密封沟槽、轴套为刚体(不可变形体)，而C形圈主材料PTFE为柔体(可变形体)。虽然C形圈弹簧是由不锈钢制成，但由于弹簧的预紧作用，弹簧的变形量较大，故将弹簧定义为可变形体，即C形圈主材料PTFE与弹簧的接触定义为deformable-deformable (即为柔-柔接触)。C形圈密封结构的有限元模型如图2所示。

图2 C形圈的有限元分析模型

C形圈力学性能的有限元分析涉及到材料非线性、接触非线性和几何非线性三重非线性问题。C形圈与轴套及密封槽的接触属于高度非线性接触。因此，必须满足接触无穿透约束条件，即满足下式：

ΔuA·n≤D

(1)

式中：ΔuA为A点增量位移向量；n为单位法向量；D为接触距离容限。本文采用具有普遍适应性的直接约束法来求解无穿透接触约束问题，该方法具有对接触描述精度高、不需要增加特殊的界面单元也不涉及复杂边界条件变化的优点。

3 C形圈材料参数的确定

C形圈由俗称“塑料王”的PTFE包裹弹簧制成，PTFE具有耐腐蚀性、耐老化、自润滑以及不粘性等优点，在密封材料领域得到了广泛的应用。PTFE作为典型的非线性大变形固体材料，常通过单轴拉伸试验来确定其材料参数。拉伸试样尺寸及形状如图3所示。按照GB/T1040—2006进行拉伸试验，试样厚度为2mm，标距为25mm。

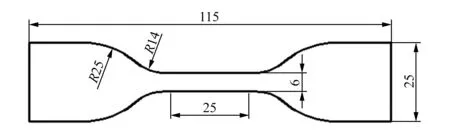
图3 单轴拉伸试样

利用有限元软件Marc中的材料试验拟合功能，将所得的拉伸试验数据进行拟合，发现二阶Mooney-Rivlin模型能够很好地拟合拉伸试验数据，并得出材料常数C01=10.7MPa，C10=0MPa。拟合结果如图4所示。

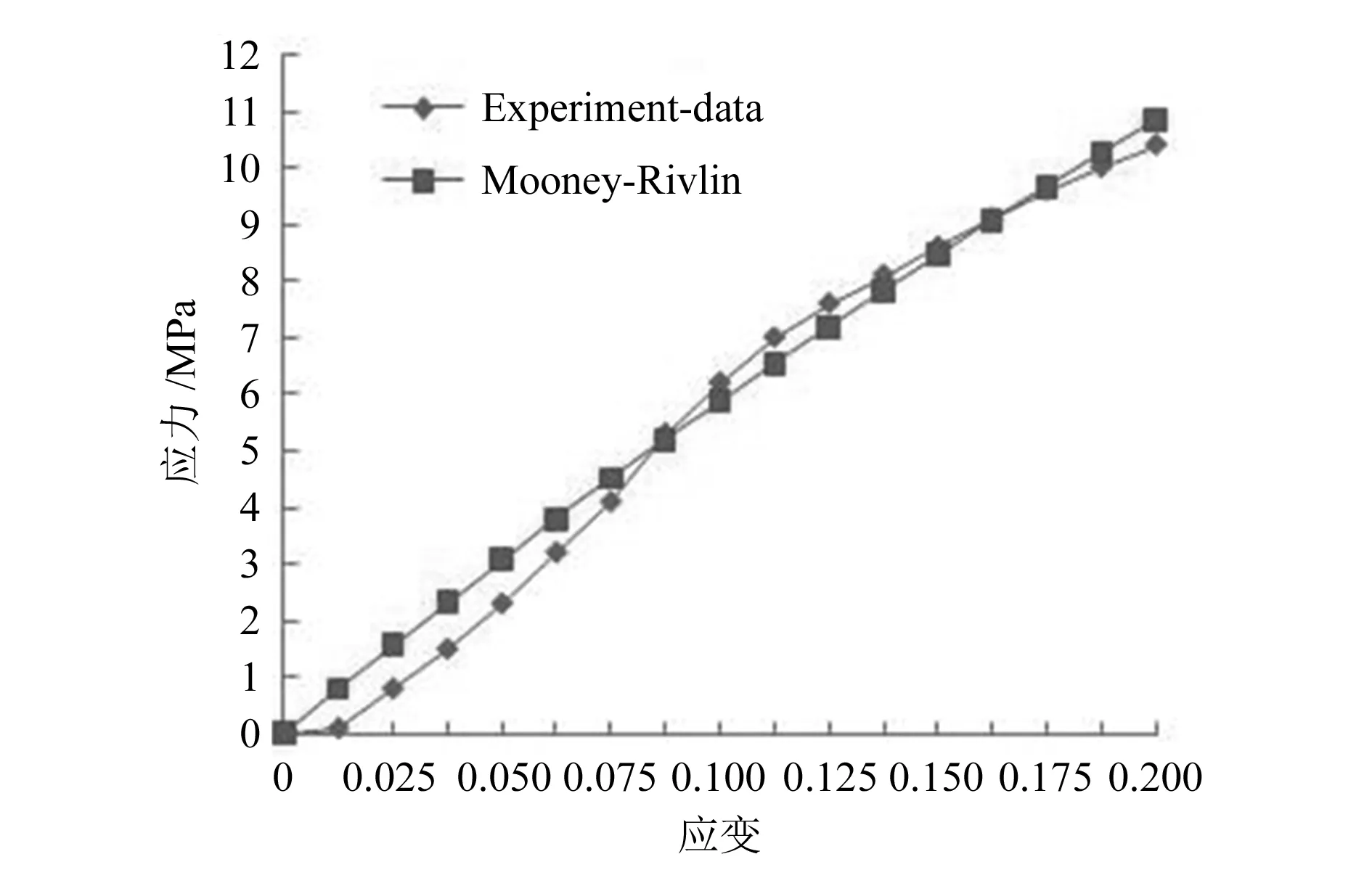
图4 Mooney-Rivlin模型拟合结果

4 边界约束条件和加载方式

用PTFE制作的C形圈密封结构的力学特性研究由两个分析步组成：第一步，通过给轴套施加Y方向的位移来实现预压缩；第二步，在第一步计算结果的基础上，在被密封的介质侧未发生接触的单元上施加垂直于边界的介质压力。

5 静力学计算结果分析

本文利用有限元软件Marc对C形圈主材料PTFE部分(以下简称C形圈)在不同压缩率ε(1.2%、1.8%、2.4%、2.9%、3.5%、4.4%)、不同介质压力P(0.5，1.0，2.0，5.0，8.0，10.0MPa)下的Von Mises应力和接触应力进行研究。

5.1 不同介质压力与最大Von Mises应力的关系

等效Von Mises应力反映了C形圈各方向上的主应力之差，它的表达式为：

(2)

式中：σ1，σ2，σ3分别为C形圈3个方向上的主应力。

一般来说，Von Mises应力值越大的区域，C形圈在该区域出现裂纹的可能性就越大，并且在该区域内会使材料刚度下降，导致密封圈的应力松弛加速，进而导致密封失效。

C形圈压缩率为4.4%时，最大Von Mises应力随介质压力变化曲线如图5所示。从图中可以得出，介质压力在0.5～2.0MPa时，随着介质压力的增大，C形圈的最大Von Mises应力值基本保持不变；当介质压力大于2.0MPa时，C形圈的最大Von Mises应力总体呈增大状态，并且增长速度较快。

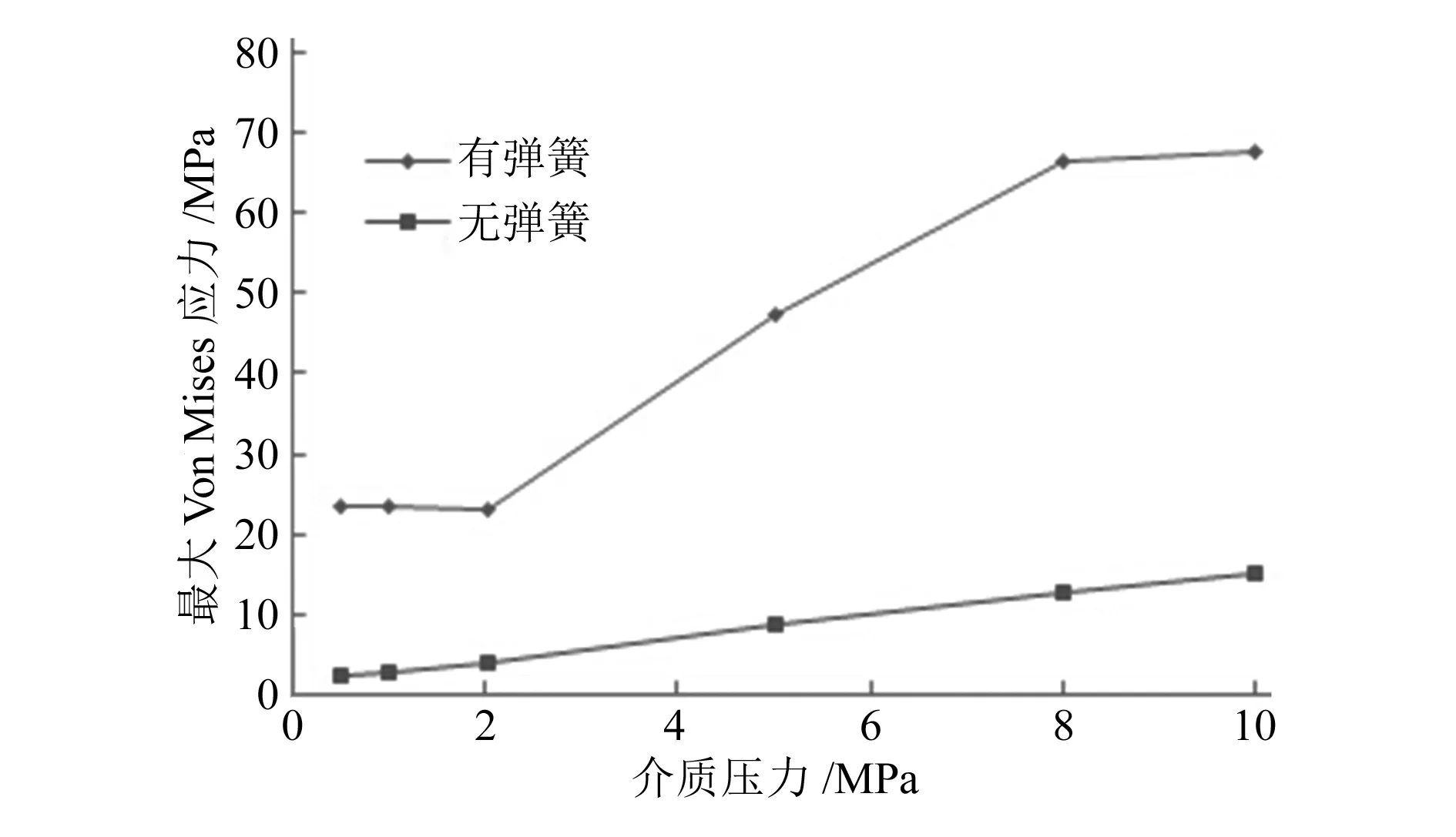
图5 C形圈最大Von Mises应力与介质压力的关系曲线

5.2 弹簧对C形圈的最大Von Mises应力的影响

去掉C形圈中的骨架弹簧对其Von Mises应力进行有限元分析，结果如图6所示。从图中可以看出，没有弹簧作用的C形圈在密封过程中产生的最大Von Mises应力明显地小于有弹簧作用的C形圈。从Von Mises应力分布云图(图6)上可以看到，没有骨架弹簧作用的C形圈Von Mises应力分布较为均匀，而有弹簧作用的C形圈Von Mises应力较为集中。说明弹簧对C形圈Von Mises应力的数值和分布影响都非常大。

图6 C形圈有弹簧和无弹簧作用下的 Von Mises应力分布云图

5.3 不同压缩率下介质压力对接触应力的影响

根据满足密封的条件，提取如图1所示主密封面2在不同介质压力和压缩率下每个横截面上的法向接触应力最大值，然后选取其中的最小值绘制如图7所示的接触应力随介质压力变化曲线。从图中曲线可知，在C形圈的压缩率一定时，此接触应力值随着介质压力的增大近似呈线性增大；同时当介质压力一定时，随着C形圈压缩率的增加，此保证密封的接触应力值也在增加。但当压缩率小于1.8%时，此接触应力小于介质压力，不能满足密封条件；当压缩率大于等于1.8%时，随着介质压力的增大，此接触应力值总是大于介质压力，能很好地满足密封条件。

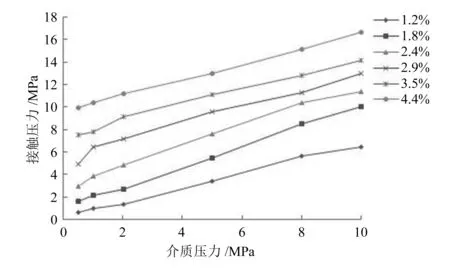
图7 接触应力与介质压力的关系曲线

6 辅助C形圈泄漏通道的形成

辅助C形圈密封结构，其密封效果是C形圈外部PTFE与被密封件接触形成接触面，通过两个接触的表面相互挤压产生接触应力而产生的。也就是说，两密封件在被相互挤压时，由于PTFE材料比较柔软，而被密封件表面不可能完全平整，总是有一定的粗糙度，因此在挤压过程中被填充在密封槽等密封部件表面的凹陷部分。在每一个密封阶段，气体泄漏的途径包括密封件表面之间的各种通道。在密封过程中，泄漏气体可通过的孔径逐渐地减小。按照泄漏通道孔径的形状，密封过程可分为3个阶段，如图8所示。

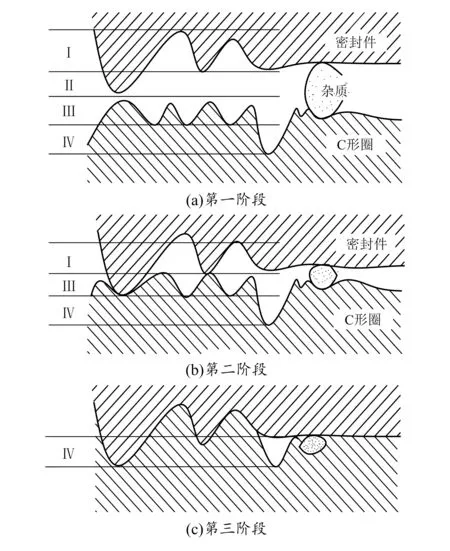
图8 C形圈的密封机理

第一阶段，作用的压紧力较小，泄漏通道孔径包括4个空间，如图8(a)所示。空间Ⅰ由被密封件表面的峰谷幅值决定。空间Ⅱ由被密封件表面加工不规则、外部杂质颗粒等能够在密封件表面产生一定空隙的因素决定。空间Ⅲ由C形圈表面的峰谷的幅值决定。空间Ⅳ由密封件表面诸如裂纹、划痕等局部缺陷决定。

第二阶段，随着压紧力的逐渐增大，表面的凸峰逐渐被压平或者嵌入到较软的C形圈里，所以空间Ⅱ消失，如图8(b)所示。由于密封件所受的压紧力较大，促使密封件表面的凸峰轮廓相互接触。

第三阶段，随着压紧力的进一步增大，两部件表面的凸峰被压平或者相互贯穿，空间Ⅰ和Ⅲ也逐渐消失，如图8(c)所示，只有空间Ⅳ部分还存在。此时要想进一步缩小泄漏通道孔径就比较困难，需要非常大的压紧力。

由此可以发现，当C形圈处于正常密封状态时，主要的泄漏通道是由C形圈表面裂纹、划痕等造成的。同时，研究发现由同心机械加工的物件表面上，径向和切向呈现出不同的剖面形状。切向的表面峰值小于径向的表面峰值。

前人用表面粗糙度记录仪观察机械加工表面粗糙度时发现，可以用波长为l、波幅为A/2的三角波表示机械加工表面轮廓，如图9(a)所示。此三角波的封闭角α一般在170°～180°范围之内，而且不可能出现小于150°的情况。同时研究还发现，可以用四面体角元素构成的规则阵列来表示由均匀机械加工所加工出来的表面痕迹，如图9(b)所示。

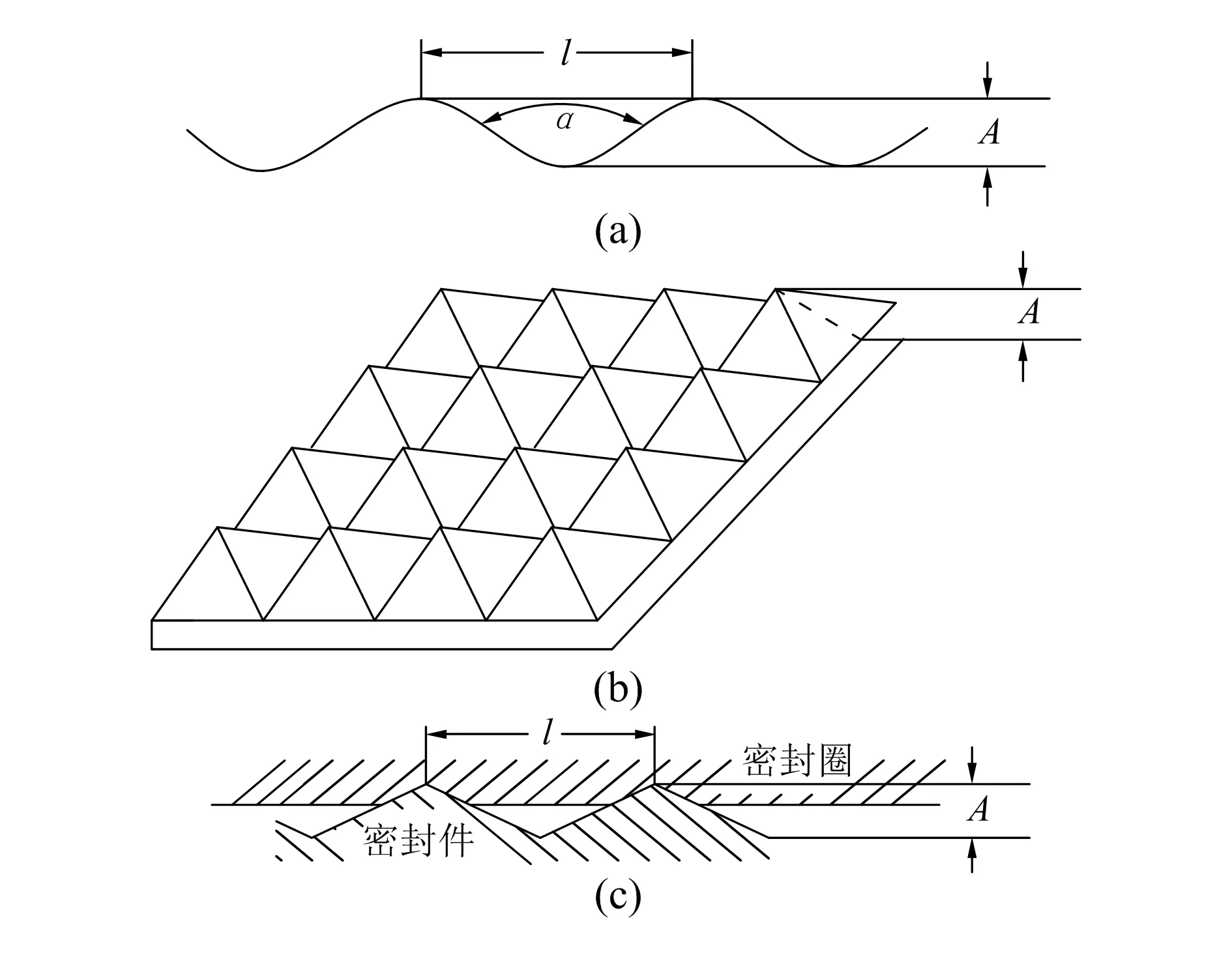
图9 被密封件表面粗糙度轮廓图

基于前人对机械加工表面粗糙度的分析，可以认为C形圈密封过程中密封表面是由被压平的等边角锥阵列或者已经嵌入较软表面中的等边角锥阵列构成，因而可以认为泄漏通道是由这些等边角锥间的间隙所形成的，如图9(c)所示。每相邻两个角锥之间的泄漏通道通常称之为单元槽。因此，在密封过程中整个密封面的泄漏通道即为所有单元槽以串联和并联方式组成的。

根据上述思想，罗思[18]基于分子流假设，提出了任何气体泄漏的总流导计算公式：

(3)

式中：T为气体的绝对温度；M为气体的分子量；A为被密封件表面粗糙度，与被密封件表面的加工精度有关；L为密封面长度，可近似为C形圈的周长；ω为密封面宽度；F为接触密封面上的总压紧力；R为密封系数，与较软材料(即密封圈材料)性质有关，经常由实验或者有限元方法求得，PTFE的密封系数R=150kg/cm2。

假设C形圈两端的介质压差为ΔP,则C形圈的泄漏率为：

Q=C·ΔP

(4)

将式(3)代入式(4)中，可得：

(5)

根据式(5)可知，要计算C形圈的泄漏量，只需知道C形圈在密封时接触密封面之间的压紧力F、接触面宽度ω以及接触长度L即可。这些未知量可通过有限元模拟的方法获得。在利用Marc软件分析结果时，提取C形圈接触表面每一节点上的接触应力，然后求其平均值得到平均接触应力。同时提取接触面的宽度，用平均接触应力乘接触面积即可得到压紧力。

6.1 压缩率对C形圈泄漏率的影响

表1为介质压力为2.0MPa时，不同压缩率下单位接触长度的数值模拟结果。

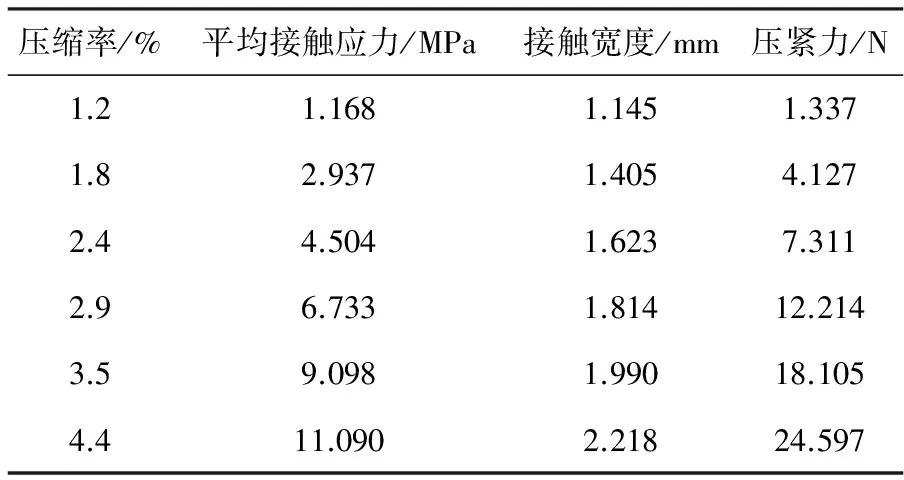
表1 不同压缩率下的数值模拟结果

由表1的数值模拟结果和式(5)，可以得到常温下C形圈泄漏率与压缩率的关系曲线，如图10所示，C形圈的泄漏率与压缩率之间近似呈双曲线关系。从图中可以看到C形圈的泄漏率随着压缩率的增加而减小，并且随着C形圈压缩率的增大,C形圈泄漏率的减小速度也越来越慢。由此可知，在保证C形圈不被破坏的情况下，适当加大C形圈的压缩率更有助于增强C形圈的密封效果。

图10 C形圈泄漏率与压缩率的关系曲线

6.2 密封件表面粗糙度对C形圈泄漏率的影响

图11为常温下被密封件粗糙度与C形圈泄漏率的关系曲线图。从图中可以看到，C形圈泄漏率随着被密封件粗糙度的增加而增加，并且泄漏率的增长速度也随着被密封件表面粗糙度的增加而增加。这是由于被密封件的粗糙度增大即表面的凸峰过高，C形圈材料PTFE不能充分地填充到被密封件的凹陷部分，使得被密封介质的泄漏通道增大，从而使得C形圈的泄漏率增加。

7 结束语

介质压力和压缩率对C形圈的Von Mises应力和接触应力的大小和分布都有很大的影响，因此在使用C形圈做密封件时，应根据不同的介质压力选择合适的压缩率，才能达到更好的密封效果，C形圈的使用寿命也会更长。本文仅利用有限元软件对C形圈的力学性能和泄漏率进行了模拟分析，在模拟过程中对C形圈的实际工况进行了简化，故与C形圈工作过程中的力学性能还是有一定的误差。由于条件的限制，本文只对C形圈进行了相关的理论研究，并没有进行实验验证，故在后续研究中，将对C形圈的密封性能进行实验研究。

参考文献：

[1] 蔡仁良，顾伯勤，宋鹏云. 过程装备密封技术[M]. 北京：化学工业出版社，2006：143.

[2] 郝一舒，祝标，赵星龙. 基于Marc对塑料—金属斜齿轮副黏弹性的有限元分析[J]. 机械传动，2014, 38(1)：67-70.

[3] 吴兴彬，李大永，唐伟琴. 聚四氟乙烯复合材料力学性能研究与有限元分析[J]. 工程塑料应用，2014,42(2)：74-77.

[4] 许珊珊，张营营，张其林. PTFE 膜材的应力松弛性能及预测模型分析[J]. 应用数学和力学，2016, 37(3)：266-276.

[5] KLAMECKI B E, SEFKOW R B, MACIEJEWSKI N J. Design of O-Rings as an example of passive structures[C]//Conference on Smart Materials, Adptive Structures and Intelligent Systems. Ellicott City, Maryland, USA: American Society of Mechanical Engineers, 2008: 439-445.

[6] MACIEJEWSKI N J, SEFKOW R B, KLAMECKI B E. Composite structure design of O-Rings using material behavior to behavior to decrease strain energy and permanent deformation[J]. Journal of Tribology, 2009, 131(4): 1-10.

[7] 吴琼，索双富，刘向锋，等. 丁腈橡胶 O形圈的静密封及微动密封特性[J]. 润滑与密封，2012, 37(11)：5-11.

[8] 杨家义，孔建，李振环，等. 全氟醚橡胶O型圈在旋转接头上的应用研究[J]. 流体机械，2011,39(6)：19-21.

[9] 马春红，白少先，康盼. 氟橡胶O型圈低压气体密封黏滞摩擦特性实验[J]. 摩擦学学报，2014, 34(2)：160-164.

[10] 沈明学，郑金鹏，孟祥铠，等. 往复轴封氟橡胶O型圈微动摩擦学特性[J].机械工程学报，2015, 49(6)：89-96.

[11] 于焕光，张秋翔，蔡纪宁，等. 机械密封补偿机构中辅助O形密封圈摩擦磨损性能的试验研究[J].流体机械，2012,40(6)：1-4.

[12] 关文锦，杜群贵.真空环境中O形密封圈泄漏分析[J].机械设计与制造，2013(4)：66-69.

[13] 李斌，刘玉魁.真空环境中受内压双重橡胶圈密封结构漏率的计算[J].真空与低温，2000,6(1)：48-53.

[14] 莫丽，王军. D形橡胶密封圈的有限元分析和改进[J]. 机械科学与技术，2016,35(7)：1018-1022.

[15] 韩传军，张杰. 矩形橡胶密封圈的有限元分析及优化[J].橡胶工业，2013,60(2):98-103.

[16] 刘明，陆军，段栋. Y型密封圈密封原理探讨与结构优化设计[J].特种橡胶制品，2012,33(3)：57-59.

[17] 于润生，杨秀萍. Yx形液压密封圈的有限元分析及结构优化[J]. 润滑与密封，2011,36(7)：66-69.

[18] 罗思·A. 真空技术[M].北京：机械工业出版社，1979.