基于装配难度计算的装配序列生成方法研究
方叶祥,汤文成,樊树海,蒋南云
(1.东南大学机械工程学院,江苏 南京 211102) (2.南京工业大学经济与管理学院,江苏 南京 211816)
装配序列优化可以提高装配效率、降低试错成本,一直是虚拟装配研究的重点。虚拟装配软件虽然具备一定的建模能力,但对装配建模、评价的能力不足;一些商用软件虽然也能进行运动干涉检验,但依然只能检验其空间几何信息之间是否相容,不能对装配过程实现量化评价[1],因而不能优化。而通过定量评价实现装配序列优化是解决此类问题的基本思路。
就现有的文献来看,对装配序列优化的研究主要是在两个阶段:第一个阶段是设计阶段的装配性评价,主要目的是通过研究可装配性来改进设计,从而得到优化的目标。许多的研究皆处于此阶段,主要采用的是智能算法,如神经网络、遗传算法、粒子群算法、规则[2]等。第二个阶段是装配过程评价。王孝义等[3]从装配操作方便性、装配精度保证性、装配工艺简单性、装配状态稳定性4个方面来评价同层装配单元的装配序列质量情况,同时建立了基础指标与准则(二级指标)之间的关系。影响产品装配序列质量的因素很多,既有定性的,也有定量的。可以将影响产品装配序列质量的因素归结为以下10个:总装配操作数、辅助装配操作数、聚合性、装配操作的并行性、装配方向、装配时间、装配成本、装配资源、零件的设计水平、零件的制造工艺水平[4]。但是这些装配评价方法在评价指标上过于关注装配序列本身,忽略了装配序列与作业人员之间的相互影响。马红占等[5]基于人因工程学的原理从人体装配需求角度出发,建立了定性和定量相结合的装配序列人因性能综合评价指标体系。另外对装配序列优化的研究还有灰色关联理论、建模法[6-8]等,但是所有的研究都只有序列的综合评价,没有给出某个动作的评价方法,对动作的可行性没有进行深入的研究。
实际装配与在图纸上虚拟装配的不同之处在于:实际装配要考虑零件的获取方式、质量、形状、运动轨迹、先后关系、空间约束以及装配需要的力量、精确程度等因素,只有每个动作都做到优化、可行,才能保证最后整个装配序列的优化。本文将装配序列评价细化到动作评价层次,建立相应的计算公式并作推论,以便在实践中快速形成装配序列方案。
1 包含动作分析的装配过程决策模型
装配序列生成是一个多层次决策问题,而传统的装配序列研究只关注一个层次上的问题,故生成的装配序列很难在实际中应用。本文将构建一个多层次装配序列决策模式以明确装配问题的内部结构,指出动作难度计算公式对整个装配序列生成的基础性作用。
装配包括由多部件构成的系统级装配以及由零件构成的部件装配。一般虚拟环境下的装配研究停留在部件组装层面。当有多个部件时,部件的装配顺序除了遵循工艺约束之外,还需要考虑前面的装配对后面装配的影响,如可能会造成后面装配的难度加大甚至装配空间不够等情形。部件的自装配也存在这样的问题。因此,必须对每个零件装配过程进行动作分析、建模、计算,才有望得到优化的装配序列。
装配过程一般是由选择零件、抓取、移动、对准、定位、组装、返回等几部分组成。其中选择零件的时候,就已经事先有了装配序列草案,这个草案遵循着一些习惯,如先下后上,先重后轻,先大后小,这些习惯实质上是解决装配的稳定性问题,即在多个变量同时存在的情况下,人们习惯于先稳定一些变量,这些变量之所以要先稳定,在于这些变量如果反复试错、优化的话,需要耗费很多时间和精力,成本会很高。在选择零件时,必须遵循一些硬约束(如工艺上的配合),通常,由图纸可以得到这样的工艺约束矩阵。
从装配工作量的角度来看,影响工作量大小的因素有零件数量、质量、主要尺寸、连接点的数量、形状等。从装配的等待时间来看,影响因素主要是与其他部件的连接特征,如可接近性、视野障碍、连接辅助等。综上,建立的装配决策过程如图1所示。
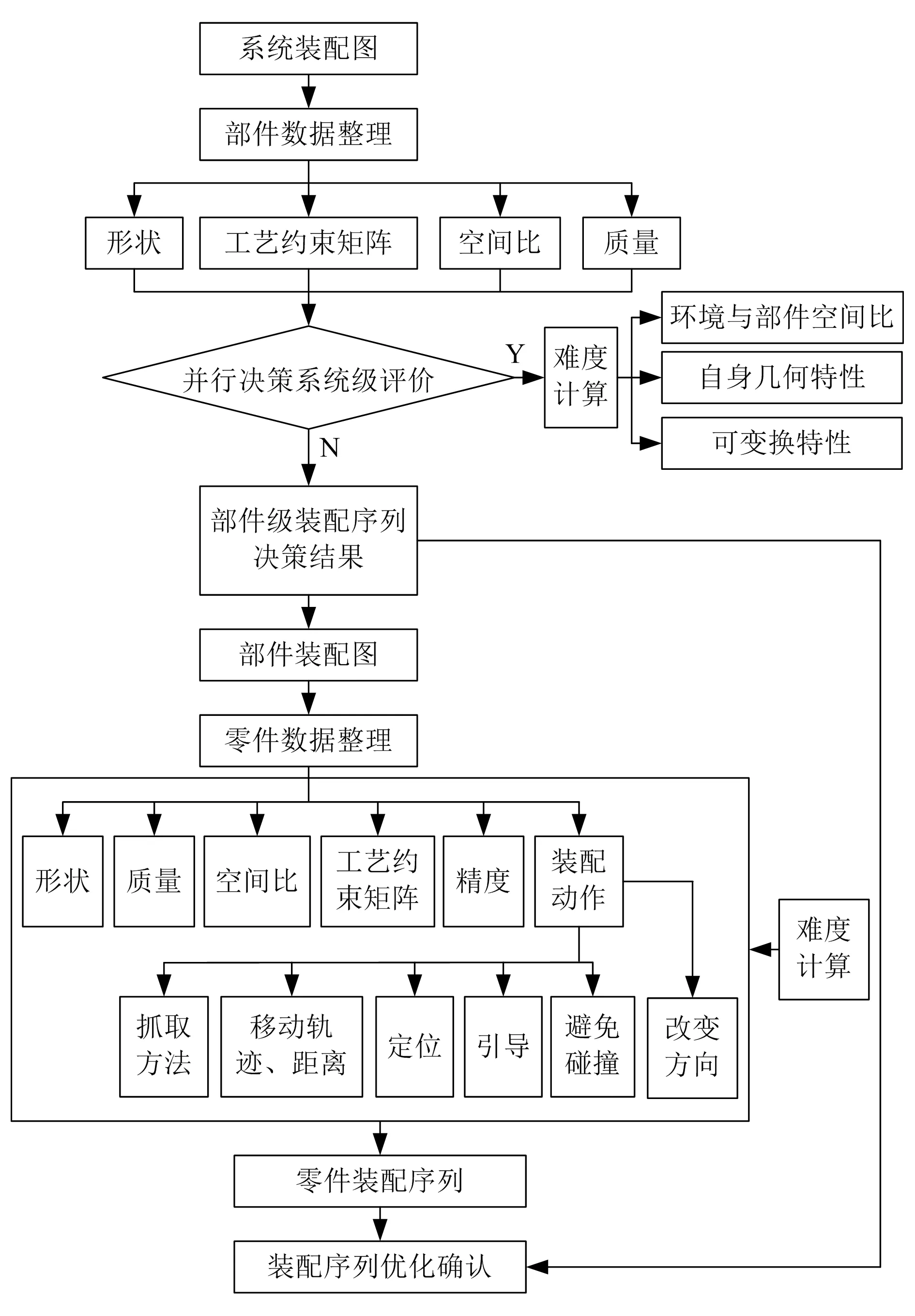
图1 装配决策过程
图中部件级的空间比是指部件体积与整个产品所占空间的比例,零件级的空间比是指零件体积与零件将被装配区域空间的比例。空间比越大装配难度越大。
2 装配难度评价方法
从工业工程实践出发,严峻[9]给出了基于装配难度的可装配性评价,文中将质量、形状大小、连接点数、有无障碍(视觉、空间)、无定位辅助、是否调整、使用工具数量作为难度考核对象。本文在此基础上,增加了动作影响因素和动作难度特征,分别为:空间比、精度、停止、方向调节、注意和方向变更、位置(包含高度、对中心的分离度)。
2.1 装配合理性原则
动作是由装配序列决定的,动作的难度反过来可以判定序列的合理性。优化的装配序列应使动作难度总和最小、能量消耗最少。从系统的角度应该追求装配难度总和最小。
2.2 基于动作的难度评价方法
鉴于装配方法会从空间、注意力、方向、姿态等多个方面影响动作执行难度和装配序列生成,因此动作难度是装配方法的函数。本文令f()表示装配方法,Ai表示第i个零件或部件的装配难度,构建如下零、部件的装配难度计算公式:
Ai=f(质量,空间比,连接点数,有无障碍(包括视觉、空间),有无定位辅助,使用工具数量,工具精度,相对于基准的高度,动作停止(即持续时间),动作方向调节,注意力(包括精度、碰撞)和方向变更,与中心位置的距离)。
(1)
式中:Kj(j=1,2,…,13)为权重;Wi为第i个零件的质量;W为所有零件质量总和;Vi为第i个零件的体积;V为部件或系统总体积;ni为连接点数量;ei,si为判断值(有为1,无为0);di为辅助定位个数;D为辅助定位总数;tn为工具数量;ci为装配精度;C为装配精度基准值;h为重物所在位置的高度;H为产品的高度;t为持有重物的时间;T为总的装配时间,aift为动作方向调节数量;dri为方向变更次数;DR为方向变更总次数;NL为精度等级,完好性等级,用努力系数表达;li为零件到对称中心(或轴)的距离;L为产品形状边缘距对称中心线(中心)的距离。
式(1)的好处在于它以动态的形式表达了不同的装配序列会产生不同的装配难度。
3 基于装配难度的装配序列推论
根据装配难度公式可以得到如下推论。
1)最优装配序列遵循难度越大越靠前原则。
证明:设有一个装配序列B1={A1,A2,A3,…,Ap,Aq,…,An},难度由大到小,假设做一个调整,将Aq提到Ap前面,序列变为B2={A1,A2,A3,…,Aq,Ap,…,An},由于Aq提前,导致Ap的空间比、增加视觉障碍和动作方向调节数量等增加,使得Ap值上升,导致序列B2的难度总和大于序列B1,因此B2不是最优序列,它劣于B1。
2)在其他条件相同的情况下,装配序列应由低到高;同一高度,应该由里向外,由中间向两边。

②当从外向里操作时,存在视觉障碍、方向变更以及持有重物的时间,因此里面零件所具有的装配难度要大于外面零件的装配难度。根据推论1,装配顺序应该自里而外。
3)先重后轻。
证明:假设有两个零件其质量分别为W1,W2,若W1>W2,则A1第一项(K1·Wi/W)的值就大于A2相应的值,A1>A2,A1就应排在A2的前面。
4) 先小后大。
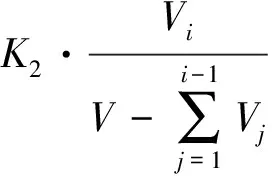
在有多个要素同时存在的情况下,基于动作完成可能性考虑,得到如下装配优先序列推论。
1) 若零件的空间比和高度比相等,则两个不同零件相比,若装配高度小于空间比倒数的平方,则高度越低越优先;否则,空间比越大越优先。
证明:设有零件J1和J2,J2的高度是J1高度的M(M>1)倍,J2的空间比也是J1的M倍,且空间比和高度比数值相同,其他条件相同,则
因零件空间比和高度比数值相同,不妨设为Z(0 根据题给条件K2=K8,得 得证。 2) 若零件的空间比和质量比相同,在其他参数相同的条件下,则空间比小、质量大的零件优先装配。 证明:设有零件J1和J2,J1的空间比是J2的M倍,J2的质量是J1的M倍,其他条件相同,则 3)零件的位置重要性由内向外逐渐降低。 以组装电脑为例,要装配的零件有内存、散热器(风扇)、硬盘、光驱、电源、CPU、显卡、机架(机箱)和主板,其装配图如图2所示,装配参数见表1,约束工艺矩阵见表2。表1、表2中,1代表有,0代表没有。 图2 台式电脑组件和装配图 表1 电脑组装件参数 零件名称质量/kg空间比连接点数距中心距离/mm有无定位辅助工具精度动作停止动作方向调节注意力(精度、碰撞)动作方向变更高度/mmCPU0.011/10004400010108散热器0.0550/100042010101010内存0.011/100012000101015主板1.001/21300100005显卡0.011/100013000101015硬盘0.501/848011000050光驱1.001/848011000070电源1.001/848011001060机架1.001/100002000100001 表2 工艺约束矩阵 根据前文推论,在排序时不需要对每个零件的难度都进行计算,只需要对不宜比较的少数零件在排序时根据公式计算、比较即可,这样可以大大节省时间。具体做法如下: 第一步,按照由低到高顺序排列。机架(1mm)→主板(5mm)→CPU(8mm)→散热器(10mm)→内存(15mm)、显卡(15mm)→硬盘(50mm)→电源(60mm)→光驱(70mm)。在这个排列顺序中,只有内存和显卡的顺序待定。 第二步,应用推论2(由内向外排列顺序)确定内存和显卡的顺序为内存(20mm)→显卡(30mm)。 根据上述两步得到装配优先序列:机架→主板→CPU→散热器→内存→显卡→硬盘→电源→光驱。但是,如果参考推论3,则电源应排在硬盘的前面,因此有必要进行一次难度值计算。由表1中参数可得:W=4 580,N=55,D=4,L=80,T=0,DR=0,令Ki=(1,2,3,…,13)=1计算得到电源的难度值为2.282 734 551,硬盘的难度值为2.156 897 578,从而得到最终装配序列为:机架→主板→CPU→散热器→内存→显卡→电源→硬盘→光驱。 为了检验上述方法的正确性,将表中参数代入式(1)分别计算各个零件的装配难度值,求解结果见表3。按照难度由大到小的顺序是:机架(71.782 976 970)→主板(16.154 704 250)→CPU(9.825 910 679) →散热器(8.633 644 303) →内存(5.938 031 891)→显卡(5.813 031 891)→电源(2.282 734 551)→硬盘(2.156 897 578)→光驱(1.866 067 884),所得结果和推论一致。推论计算的复杂度比装配难度值计算大大降低,便于在实时环境下快速给出结果,提高工作效率。 表3 各个零件装配难度值计算结果 本文对13个装配动作难度考核对象进行研究,给出了装配难度的定量化定义,然后进行推论、证明,得到最优装配序列的7个推论,并以电脑组装为例,说明了推论的可行性和其具有较低的计算复杂度。限于篇幅,本文暂未对系数的取值作研究,实际工作中,可将这些系数看作权重,由企业自己确定其大小。 参考文献: [1] 李慧,毛君,白金. 基于Web的产品装配评价建模研究[J]. 四川大学学报(工程科学版), 2007,39(增刊1):146-150. [2] 祁新梅. 基于规则的可装配性评价及其接口技术[J]. 机械与电子,1999(6):22-23. [3] 王孝义,张友良,张 帆. 装配序列评价研究[J]. 中国机械工程,2005(13):1165-1170. [4] 周开俊,李东波,许焕敏. 一种产品装配序列的评价方法[J]. 计算机集成制造系统,2006(4):563-567. [5] 马红占,褚学宁,刘振华,等. 基于人因仿真分析的装配序列评价模型及应用[J]. 中国机械工程, 2015(5): 652-657. [6] 朱晓林,黄敏纯,章嘉琼,等. 基于灰色关联理论的装配序列评价研究[J]. 盐城工学院学报(自然科学版),2011(1): 44-47. [7] 张刚,侯强,李火生,等. 复杂结构产品装配序列评价方法研究[J]. 机械设计与制造,2007(1): 132-134. [8] 张嘉易,王成恩,马明旭,等. 产品装配序列评价方法建模[J]. 机械工程学报, 2009(11): 218-224. [9] 严 骏. 基于装配难度指标的可装配性评价系统[J]. 上海汽车,2013(3):39-43.



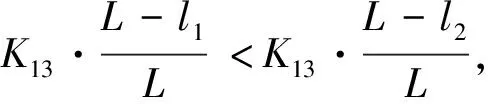
4 应用案例



5 结束语

