UP50工业机器人加工大直径螺纹的运动学分析

张永贵，邹 琰，黄中秋，程 兵

(兰州理工大学机电工程学院，甘肃 兰州 730050)

工业机器人是现代工厂实现生产自动化、信息化的重要装备，可用于焊接、喷涂和搬运等作业。如果在工业机器人末端装上相关驱动装置和刀具，即可代替机床的加工进给运动，这将有助于解决传统机床在施工现场加工大型零部件时存在的装夹困难、运输成本高、耗费时间长等问题。如大直径螺纹[1]在施工现场损坏后，如运用机器人可实现现场直接加工修复，那么以上的问题将会得到较好的解决。本文以机器人在不同进给速度下，加工不同大直径螺纹为实例，分析总结机器人各关节在关节空间的变化情况，以便为进行关节空间螺旋轨迹规划获得更好的基础条件。

由于现在大部分工业机器人采用的插补方式是直线插补和圆弧插补，很少采用螺旋插补，因此可以借鉴工业机器人在笛卡尔空间的轨迹规划方法和数控机床螺旋插补原理，对螺旋线进行插入节点分割，在保证一定精度要求的前提下，在两个分割节点之间运用机器人现有插补方式进行插补，以达到运用工业机器人进行螺旋插补的目的。

1 工业机器人Motoman UP50模型的建立

1.1 机器人运动学正解

采用D-H法[2]建立机器人的运动学方程。定义机器人不同位姿时，坐标系{i+1}与坐标系{i}的变换矩阵为：

(1)

式中：zi为坐标系{i}中的z轴；θi为机器人第i个关节角；βi，di，αi，ai为机器人零位时的连杆参数值。本文采用后置坐标系方法[3]建立机器人坐标系，如图1所示，得到的Motoman UP50对应连杆参数[4]见表1。

图1 D-H坐标系 表1 机器人连杆参数表

αi/(°)βi/(°)ai/mmdi/mmθi/(°)-90-901450θ118008700θ2-9001100θ39000-1025θ4-90000θ518000-175θ6

表中：αi为zi-1轴绕xi-1轴旋转至zi轴时的扭角，正负通过右手法则判断；βi为机器人在零位时各关节的关节角度；ai为zi-1轴与zi轴之间的公垂线长度，正向与xi一致；di为xi-1轴沿zi轴移动至xi轴时的位移，正向与zi一致；θi为xi-1轴绕zi轴旋转至xi时的转角，正负通过右手法则判断。

将表1的连杆参数代入式(1)，得到各连杆变换矩阵：

式中c1为cosθ1，s1为sinθ1，以此类推。

根据以上连杆变换，即可推导机器人末端坐标系与基坐标系之间的变换矩阵，如式(2)所示：

(2)

即：

(3)

式中：p为刚体在固定坐标系中位置的齐次坐标表示形式；n，o，a为刚体坐标系的轴和固定坐标系的轴之间的方向余弦，并用齐次坐标形式的(4×1)列阵分别表示。式(3)即为UP50型机器人运动学的正解。

1.2 机器人运动学逆解

求解机器人运动学逆解的方法有很多，在此应用代数法[5]来求解Motoman UP50工业机器人运动学逆解。

θ1=arctan[2(175ay-py,175ax-px)]

(4)

θ2=arctan[2(A2,B2)]-arctan{2[C2/ρ,

(5)

式(5)中正负号对应于θ2的2个解，在求解具体工业机器人运动学逆解时，可通过数据验证确定正负号[6]。

θ3=arctan[2(110B3+1 025A3,110A3-1 025B3)]

(6)

θ4=arctan[2(B4,A4)]

(7)

θ5=arctan[2(-A4,175B5c4)]

(8)

θ6=arctan[2(B6,A6)]

(9)

2 普通螺旋线

设螺旋线的半径r=50mm，螺距p=6mm(以下如不特殊说明，都是以mm为单位)，螺旋倾角为ψ0。假设螺旋线轴线与工件坐标系{W}的z轴重合，且起始点从其x轴开始，螺旋线的空间坐标原点为(xt，yt，zt)=(0，0，0)，则螺旋线在工件坐标系{W}中的参数方程[7]如式(10)所示。

(10)

式中：φ为参数变量。

螺旋倾角ψ0可由式(11)得出：

(11)

φ从0到p变化一次，生成一个螺距的螺旋线。运用MATLAB可显示在基坐标系{o}下的螺旋线图形，如图2所示。

图2 螺旋线

3 倾斜螺旋线各节点的位姿

3.1 截取节点

螺旋线是机器人末端执行器的运动路径，如果要对螺旋线轨迹进行规划，就必须在螺旋线上截取一系列的路径节点，而且这些节点的位姿需用齐次矩阵的形式表示出来。

采用折线拟合螺旋线的方法[8]，向xoy平面投影(如图3所示)。设步进角为αc，控制误差为δmax(普通数控加工误差可取0.01mm)[9]。

在xoy平面上：

即：

αc≤2·arccos(1-δmax/r)

(12)

根据步进角选取节点，节点数为：

n=ceil(2·π/αc)

式中：ceil为MATLAB函数。向正无穷取整得到的n为158。

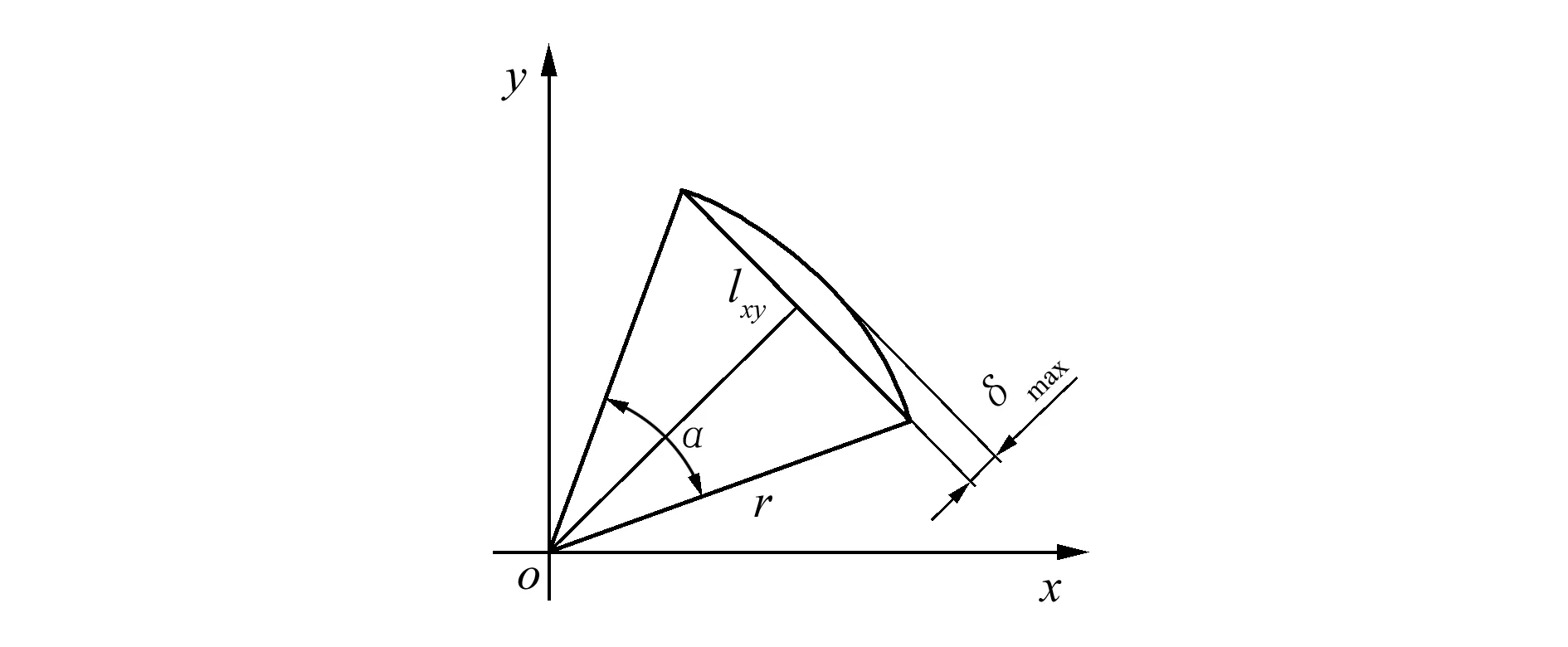
图3 投影图

3.2 节点姿态和位置

为了得到更精确的分析结果，取3个螺距的螺旋线进行分析、研究。

3.2.1节点位置

由上可知，在螺旋线上截取的节点数为n，则螺旋线方程式(10)中变量φ的步进为p/n。现假设φ从0每隔p/n取点，到3p为止，然后通过螺旋线方程式(10)可得各节点在工件坐标系的位置坐标(xW(i),yW(i),zW(i))。机器人末端坐标系原点的齐次矩阵序列TW(:,:,i)如式(13)所示：

(13)

(14)

3.2.2节点姿态

假设在开始控制机器人时，机器人末端刀具上空间直角坐标系3个坐标轴的方向与参考坐标系各坐标轴的方向对应一致。已知刀具旋转轴线与关节6轴线夹角为90°，末端坐标系yoz平面是砂轮所在平面，末端坐标系的x轴方向是电主轴所在方向。具体变换如下：

1)空间直角参考坐标系固定不动，使与机器人末端刀具固接的空间直角坐标系绕空间直角参考坐标系的y轴旋转-π/2，这样会让机器人的末端坐标系轴x与空间直角参考坐标系的z轴重合，此时呈竖直向上的形状。

2)将与机器人末端执行器固接的直角坐标系再绕空间直角参考坐标系的z轴旋转π，这样会让机器人的末端坐标系z轴方向与空间直角参考坐标系的x轴重合。

4)以上已经假设过此空间螺旋线的倾角为ψ0，因此使机器人末端坐标系绕空间螺旋轴k旋转ψ0，最终可得到机器人末端坐标系姿态矩阵Tr。

经过以上4步变换后，可以得到与机器人末端执行器固接的空间直角坐标系姿态矩阵Tr。调用MATLAB函数angvec2tr()可得节点姿态矩阵Tr，具体表达式如式(15)所示：

Tr=angvec2tr(ψ0,k(i,:))·Rot(x,π/6)·Rot(z,π)·Rot(y,-π/2)

(15)

式中空间螺旋轴k是在空间螺旋线上随着机器人末端位置改变而不断变化的单位方向向量(机器人末端沿螺旋线上升过程中，出现在每个节点所处圆平面上的圆半径方向，方向朝里)，k的数学计算公式在MATLAB中可用数学函数reshape()[10]得到。具体表达式如式(16)所示：

zeros(1,3n+1)],3n+1,3}

(16)

由此可知，k是一个(3n+1)×3阶矩阵，矩阵的每一个行向量代表对应节点的螺旋轴单位方向向量。

最后，在得到节点位置矩阵和姿态矩阵后，运用MATLAB循环程序将两者融合成节点位姿矩阵T(:,:,i)，矩阵T是4×4×(3n+1)阶矩阵，即(3n+1)个节点在基坐标系{o}的位姿矩阵序列，节点位置如图4所示。

图4 节点位置

4 验证机器人模型

因为本实验取3个螺距的螺旋线进行分析、研究，所以总节点数为3×158+1=475。

取第一个节点来验证机器人模型正、逆解准确性，并确定唯一逆解。由以上MATLAB程序可得前两个点的位姿序列如下：

求节点1在关节空间对应的位移向量。在式(5)的计算中，分别取负号、正号，可得：

将q1代入式(3)中，得

将q2代入式(3)中，得

经过比较发现：取正号时，求解的位姿与实际位姿相差非常大；而取负号时，误差则非常小。综上可知：在求解θ2的式(5)中，取负号满足计算要求。

5 螺旋线各节点的位移、速度、加速度向量图像

5.1 各节点关节空间的位移向量

对运动学逆解表达式(4)～(9)进行编程，可得475个节点在关节空间的位移向量。通过MATLAB可分别显示6个关节在各节点关节角的连线，使6个关节在关节空间的关节角变化更直观，如图5所示。

图5 关节角

5.2 各节点关节空间的速度向量

关节速度求解公式，如式(17)所示：

(17)

式中：J(q)为机器人雅克比矩阵，是6×n的偏导数矩阵。

工业机器人末端在工作空间的速度表示为：

设机器人末端在z轴方向为恒速：

vz=0.2mm/s

(18)

则第i个节点的其余速度分量可表示为：

vx(i)=wz(i)·r·sin[(i-1)·αc]

vy(i)=wz(i)·r·cos[(i-1)·αc]

用矢量积法计算Motoman UP50工业机器人的速度雅克比矩阵，并用特殊点验证雅克比矩阵的准确性。

计算J内元素的方法相同，本文只给出J1各元素：

J=[J1J2J3J4J5J6]

J1=[j11j21j31j41j51j61]

(19)

j11=-145s1-870s1s2-110s1s(2-3)-1 025s1c(2-3)-175s1c(2-3)c5-175c1s4s5-175s1s(2-3)c4s5,j21=145c1+870c1s2+110c1s(2-3)+1 025c1c(2-3)+175c1c(2-3)c5-175s1s4s5+175c1s(2-3)c4s5,j31=0,j41=0,j51=0,j61=1。

为了验证得到的速度雅克比的准确性，计算q=[0 0 0 0 0 π/2 0]时的机器人雅克比，结果为：

如J的第一列为[0 1 170×dθ10 0 0 dθ1]，则表示在位姿q=[0 0 0 0 π/2 0]时，关节1的微分转动dθ1反映到末端在基坐标系下的微分运动为[0 0 0 0 π/2 0]，由此可知速度雅克比是准确的。

已知速度雅克比矩阵、操作空间的机器人末端速度，可获得475个节点在关节空间的速度向量。通过MATLAB可分别显示6个关节在各节点角速度的连线，使6个关节在关节空间的角速度变化更加直观。

图6 关节角速度

5.3 各节点关节空间加速度向量

机器人末端加速度方程为：

(20)

其中：

(21)

式中：Hmn为雅克比矩阵J的第m行n列元素Jmn对q的偏导数，为6×1矩阵。

引进矩阵层如下所示：

(22)

称H为二阶系数矩阵，并规定

(23)

结合式(20)～(23)有：

(24)

根据式(24)可算得Hmn，最后可得二阶系数矩阵H。

对式(24)编程，求得475个节点在关节空间的加速度向量。通过MATLAB可分别显示6个关节在各节点角加速度的连线，使6个关节在关节空间的角加速度变化更加直观，如图7所示。

5.4 不同加工速度加工不同直径螺纹

采用上述计算、仿真过程，得到以不同速度vz加工不同直径螺纹的全部结果。例如：用vz=0.1mm/s的速度分别加工直径64mm～280mm的螺纹，其他亦是如此。

vz分别取0.1mm/s、0.2mm/s、0.4mm/s、0.5mm/s、0.8mm/s、2mm/s、3mm/s、4mm/s、5mm/s。

图7 关节角加速度

普通大直径螺纹参数见表2。

表2 螺纹参数 mm

6 结论

1)相同的速度(vz)下，随着加工螺纹直径的增大，各关节位移变化幅度增大，速度变化幅度增大，加速度变化幅度减小。

2)相同加工直径下，随着加工速度的增大，各关节速度增大，加速度也增大。

3)机器人有针对地修复加工大直径螺纹，可大大提高其加工精度和效率。

参考文献：

[1] 彭成勇，楼一珊，曹元平，等.钻铤螺纹连接疲劳失效研究[J].石油钻探技术，2006，34(6)：20-22.

[2] HAYATI S A. Robot arm geometric link parameter estimation[C]//Decision and Control. [S.l.]:IEEE,1983:1477-1483.

[3] 龚振邦，王勤悫. 机器人机械设计[M]. 北京：电子工业出版社,1995:44-111.

[4] 熊有伦. 机器人技术基础[M]. 武汉：华中科技大学出版社,1996:15-30,94-115.

[5] MAYER G E. Differential kinematic control equations for simple manipulators[J]. IEEE Translation on Systems,Man,and Cybernetics,1981,11(6):456-460.

[6] 张永贵，刘晨荣，刘鹏.工业机器人运动学逆向建模[J]. 机械设计与制造,2014,11(3):123-126.

[7] 罗良玲，刘旭波.基于时间分割法的圆柱螺旋线直接插补算法[J].南昌大学学报(工科版),2001,23(4):57-59.

[8] 黄建. 数控加工空间运动平滑路径的规划[D]. 扬州：扬州大学，2013：17.

[9] 陈萧. 大口径螺纹加工的分析和实现[J].南通职业大学学报，2009，23(2)：98-101.

[10] 陈富久. 基于Robotics Toolbox的工业机器人螺旋轨迹研究[D]. 兰州：兰州理工大学，2016：39-42.