基于动态剩余刚度的GFRP筋拉伸疲劳损伤研究

金清平，汪光波，于翰林

(1.武汉科技大学城市建设学院， 武汉 430065；2.中建五局第三建设有限公司，长沙 410007)

0 前言

在纤维增强聚合物(FRP)中，GFRP因其轻质高强、耐腐蚀、低成本得到了广泛应用，GFRP筋结构的疲劳损伤和破坏是工程应用中需要重点关注的问题。针对FRP材料的损伤定量定义有2种方法。一种是从微观角度出发，通过某区域内纤维脱胶、断裂的数量，以及基体裂纹的长度、密度、裂纹间隔，电阻抗，声发射等来实现；另一种是从宏观角度出发，通过剩余强度、剩余刚度、滞后能及阻尼系数等来定义损伤。材料微观结构的改变是其宏观性能改变的本质原因，微观模型仅能反映宏观尺度材料性能的趋势，可以帮助理解材料性能的劣化机理，但并不能定量精确描述其宏观尺度材料性能的改变，从微观角度出发需要比较尖端的设备及技术，不易实现。宏观特性的改变是微观结构改变的具体体现，而实际应用中更多的是需要从宏观上定量表征其损伤，故从宏观角度出发，既避免了上述难点又显得直接、高效、可靠。

剩余刚度[1-2]和剩余强度[3-4]是表征复合材料疲劳损伤的2个常用指标。文献[5-7]基于不同的损伤定义及理论提出了FRP层合板材料的疲劳损伤模型。采用剩余强度评价疲劳损伤虽然遵循了材料破坏的天然物理准则，但一个试件仅能得到一个实验数据，从试验角度看，要研究其损伤机理及规律需要大量的试验，往往不太现实。而采用剩余刚度，此指标易测量且易实现无损、全程、连续地测量，故众多学者建议采用剩余刚度定义疲劳损伤。

FRP复合材料疲劳损伤的研究主要集中在FRP层合板，而针对FRP筋材的研究相对较少，研究成果并不完善。孙志刚[8]研究了对碳纤维(CFRP)复合材料和锚具组装件开展疲劳试验，对疲劳寿命公式提出了修正。张新越、欧进萍等[9]进行了不同循环应力下CFRP筋的常温疲劳试验，CFRP筋具有很大的脆性,需要有足够的强度安全系数,才能发挥作用；根据试验拟合的疲劳寿命曲线，CFRP筋的疲劳性能远高于Q235光圆钢筋。有研究学者认为，纤维种类、环境条件、荷载类型等均是影响FRP筋抗疲劳性能的主要因素，其影响因素较多，目前比较缺乏系统性的研究。

本文对GFRP筋开展了不同应力水平、应力比下的低周反复荷载加载试验，结合FRP经典剩余刚度理论、模型和试验所得刚度退化曲线，探讨了不同加载参数对其损伤的影响，分析了GFRP筋损伤演化规律与机理。

1 实验部分

1.1 主要原料

聚乙烯基GFRP筋，材料密度为1.9～2.2 g/cm3，表面呈螺纹状，直径分别为16、20 mm，深圳海川新材料科技有限公司。

1.2 主要设备及仪器

电液伺服疲劳试验机，PLU-1000，最大荷载为-300～300 kN，加载频率为0.5 Hz。

1.3 样品制备

如图1所示，采用无缝钢套筒内填充膨胀水泥来固定GFRP筋体的两端，两端钢套筒的锚固长度均为200 mm，试样中间段的净长度为400 mm；套筒上焊接表面粗糙的钢片增大与夹具的摩擦力，试件中间段均匀喷上白漆便于观察。

图1 试验试件Fig.1 Test specimens

1.4 性能测试与结构表征

根据美国材料与试验协会(American Society for Testing and Materials，ASTM)的D3039/D3039M-14[10]以及D3479/D3479M-12[11]规范要求开展试验；试验应力水平(S，最大应力与静态拉伸极限强度之比)分别取0.3、0.5、0.6，应力比(R，最小应力与最大应力之比)分别为0.3、0.5；本试验在常温常压环境下，通过对同批次GFRP筋进行静态拉伸试验，得到其静载平均极限拉伸强度为676 MPa；按照试验设定的应力水平和应力比计算其所需的平均拉力(Pm)及拉力幅值(Pa)；试验开始前对筋体进行编号标记，“d16-R0.5-S0.6”表明对直径为16 mm的GFRP筋体采用R=0.5的应力比、S=0.6的应力水平进行试验。

2 结果与讨论

2.1 疲劳损伤理论模型

复合材料的力学性能存在较大的分散性，在相同循环荷载下的不同试件，其剩余刚度及寿命亦可能存在较大分散性。剩余刚度退化演化历程大体分为3个阶段[12-13]，如图2所示。以剩余刚度[E(n)]来定义GFRP筋在反复荷载下的损伤(D)，以寿命比(Nf，n/N)为自变量，E(n)可表示为寿命比的函数，如式(1)、式(2)所示。

(1)

(2)

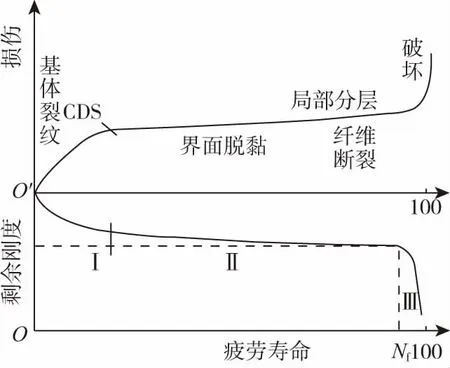
图2 复合材料疲劳损伤机制及刚度退化规律Fig.2 Fatigue damage mechanism and stiffnessdegradation law of the composites

式中E(0)——初始刚度

E(n)——n次荷载循环作用后的刚度

根据对FRP层合板的研究提出的众多刚度退化模型中，Yang[14-15]的模型考虑到了材料性能的分散性，结合了概率的方法，是一种较成功、适用性较强的模型，使用比较广泛。Echtermeyer等[16]根据大量试验数据提出其模型。2种刚度退化模型形式简单，参数较少，意义明确。2种模型表达式及参数等见表1。

表1 2种刚度退化模型Tab.1 Two stiffness degradation models

2.2 动态剩余刚度退化规律与筋体损伤分析2.2.1 动态剩余刚度退化规律

参照式(1)和(2)关于剩余刚度的表达式，比较在疲劳荷载作用下材料动态刚度的变化，以揭示疲劳对筋体材料的损伤规律。本文中用动态荷载每一周期起止段的割线刚度表示动态刚度，以寿命比(Nf)为自变量，初始刚度[以E′(0)表示]和破坏刚度[以E′(n)表示]分别为疲劳加载中的最大动态刚度和n次循环时的动态刚度，取值与前述E(0)，E(n)的取值有所区别。根据试验结果，绘制动态剩余刚度与寿命比曲线，如图3所示。

试验选用了16、20 mm 2种直径的GFRP筋体，直径16 mm的GFRP筋体采用的应力比、应力水平组合分别是R0.3～S0.6、R0.5～S0.3、R0.5～S0.5，直径20 mm的GFRP筋体采用的应力比、应力水平组合分别是R0.5～S0.3、R0.5～S0.5，其动态剩余刚度曲线分别对应为图3(a)～3(e)。从动态剩余刚度退化曲线可知：当采用相同的应力比、应力水平，不同的直径时，如图3(b)，直径16 mm的筋体在初期(0～0.1Nf段)，动态剩余刚度迅速硬化，在0.1Nf～Nf段，动态剩余刚度逐渐退化，直至破坏；如图3(d)，直径20 mm的筋体，在初期的动态剩余刚度硬化时间更短，在整个疲劳加载中剩余刚度变化平缓，主要呈现为逐渐退化，直至破坏。两者在初期的硬化时间均较短，在衰退过程中均表现比较平缓，直径16 mm筋体破坏前的动态剩余刚度约为最大动态剩余刚度的0.9倍，而直径20 mm约为0.92倍，相差不明显。由图3(c)、(e)，直径16 mm筋体的动态剩余刚度直接开始退化衰减，在0.8Nf以前，变化趋势较平缓，下降幅度小，在0.8Nf时，动态剩余刚度约为其最大值的0.9倍，在0.8Nf以后，刚度迅速减小，直至试件断裂；直径20 mm筋体的动态剩余刚度没有明显的硬化，但初期有较明显的退化，0.2Nf时，刚度退化到0.86，之后刚度退化趋势较缓，相对稳定，直至最终试件断裂，后期未出现明显的刚度陡降，与直径16 mm筋体刚度衰减趋势不同。

由上比较可知，在较小应力水平(S=0.3)、中等应力比(R=0.5)条件下，试件尺寸对疲劳性能影响较小，呈现相同的规律；在中等应力水平(S=0.5)、中等应力比(R=0.5)条件下，不同直径呈现不同的变化规律，直径16 mm与20 mm筋体的刚度退化明显不同。比较同一直径、应力比，不同应力水平下试件的疲劳性能，如图3(b)、(c)，两者在加载初期及后期呈现完全不同的退化规律，初期均出现逐渐衰减，在0.8Nf时，两者衰减幅度相差不大，均约为0.90，但在0.8Nf之后，应力水平S=0.5时的衰减比S=0.3时急剧。而直径20 mm的GFRP筋体在R=0.5，不同应力水平下，变化趋势均为逐渐退化，在S=0.5的加载条件下，破坏前衰减的幅度要大，达到0.84，而在S=0.3下，破坏前约为0.92。说明相同直径、相同应力比，不同应力水平疲劳加载时，GFRP筋体也呈现不同的刚度退化，在S较大的加载下，试样的刚度退化较严重。当用较小的应力比、较大的应力水平加载时[如图3(a)]，与中等应力比、较小应力水平加载[如图3(b)]时相比较，前期变化趋势相似，出现刚度短时间内硬化，然后逐渐衰减。较大的应力水平(S=0.6)下约达到0.8Nf时，对应的动态剩余刚度约为0.96，之后会出现急剧下降，说明较大应力水平对筋体的疲劳寿命影响大，在之前筋体的刚度反而衰减减小，说明较小的应力水平在疲劳加载中对筋体的损伤更小。

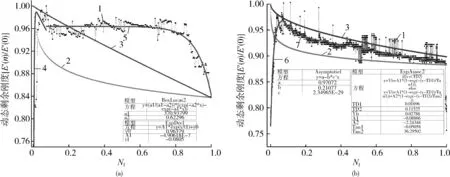
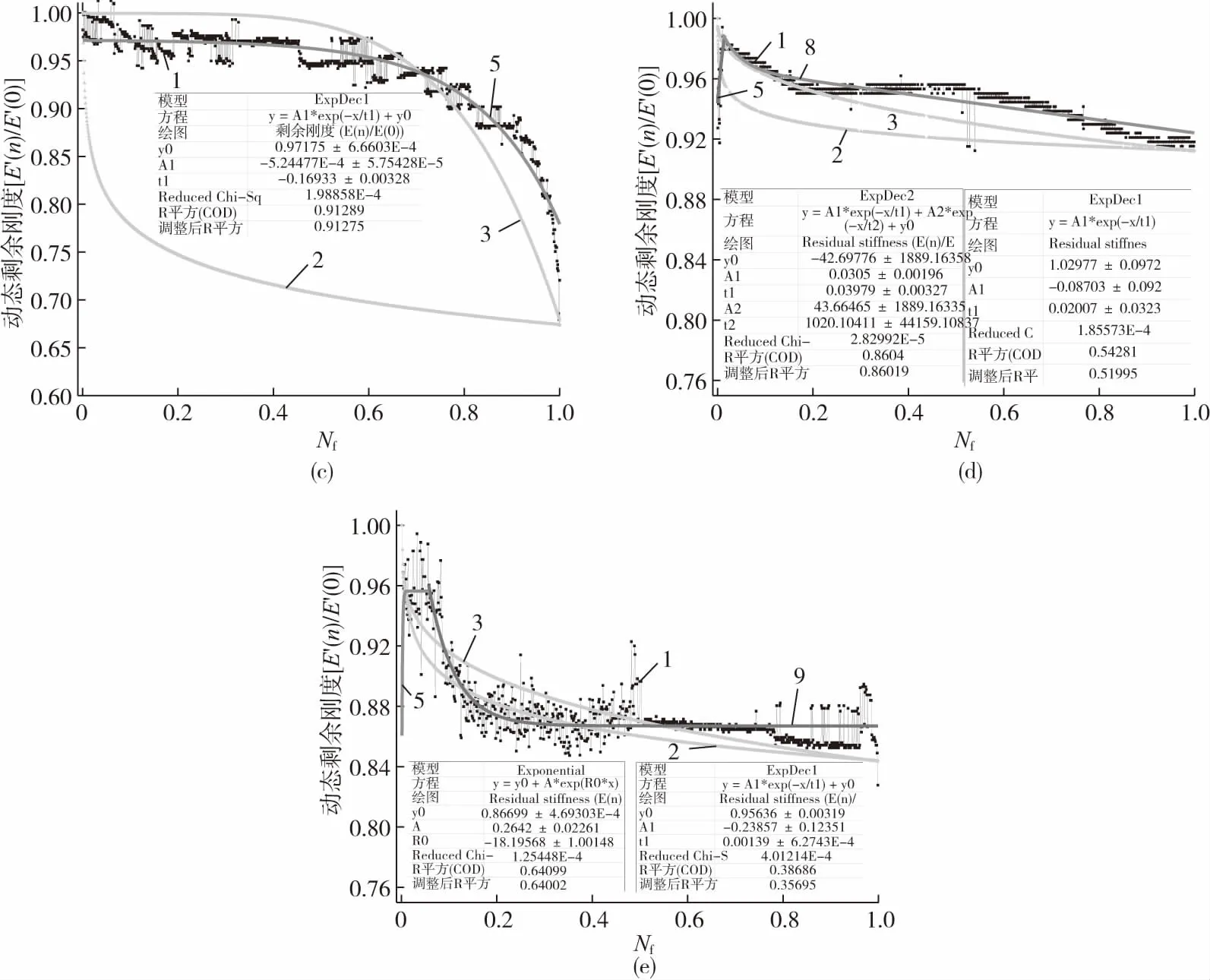
1—实验值 2—EEB模型 3—YLS模型 4—BoxLucas2模型 5—ExpDecl模型 6—Asymptoticl模型7—ExpAssoc2模型 8—ExpDec2模型 9—Exponential模型(a)d16-R0.3-S0.6 (b)d16-R0.5-S0.3 (c)d16-R0.5-S0.5 (d)d20-R0.5-S0.3 (e)d20-R0.5-S0.5图3 GFRP筋动态剩余刚度退化试验曲线及拟合曲线Fig.3 Test and fitting results of dynamic residual stiffness degradation curves for GFRP bars

2.2.2 材料损伤分析

本试验GFRP筋动态剩余刚度退化曲线来看，图3(a)、(b)、(d)、(e)均出现了刚度早期先增长的现象，与图2所示FRP层合板典型的正则化刚度曲线规律有所不同。结合拟合曲线，将动态反复荷载下GFRP筋的刚度退化演变规律分为3个阶段：第Ⅰ阶段，这一阶段因为不同的筋体会表现出有差异的刚度变化，有些筋体表现为表层基体薄弱部分产生微裂纹并沿周围扩展，筋体内部产生应力重分布，逐渐由纤维、基体复合体共同承担荷载作用，刚度达到最大时标志着此阶段的结束，此阶段内由于较少的荷载作用次数并未对筋体造成主要损伤，而是使得筋体各种缺陷得以消除，筋体性能复合性能达到最佳。同时，这一阶段中有些筋体表现出来的性能没有缺陷消除过程，刚度在荷载作用初期没有先增大再减小的现象，而是呈现出基体裂纹张开，伴随部分纤维断裂，在部分截面各微裂纹形成一定长度的纵向贯通裂纹，随着荷载反复作用，更多为裂纹贯通，筋体复合性能逐渐削弱，刚度迅速下降。第Ⅱ阶段，纤维与基体界面脱黏、剥离，纤维随机断裂等损伤耦合发展，刚度呈现出非线性缓慢下降趋势。第Ⅲ阶段，局部应力集中，耦合损伤集中演化并加剧，随之纤维大规模断裂，GFRP筋破坏。从各阶段所占寿命周期比例来看，第Ⅰ、Ⅱ阶段为筋体的有效寿命期，大约占整个寿命期的70 %左右，刚度相对稳定，在荷载作用下筋体损伤在不断累积，但并未造成筋体性能的明显退化。第Ⅲ阶段筋体性能退化较快，约占整个寿命周期的30 %左右，刚度极不稳定，会产生急剧变化并发生破坏。

2.3 动态剩余刚度与寿命关联模型

结合YLS、EEB模型，对试验结果进行分析，并拟合试验数据，如图3所示。EEB模型函数为对数函数，模型曲线本身能表达出复合材料刚度退化规律中先急剧下降后缓慢下降的规律，但模型曲线与试验曲线在下降阶段及幅度上吻合不佳，如图3(a)、(c)、(d)所示，模型曲线与试验曲线呈月牙形，曲线走势完全不同，图3(b)模型曲线与试验曲线在0～0.20Nf段位于试验曲线下方，开始时相差幅度较大，而后逐步减小，图3(e)模型曲线与试验曲线在0.20～0.60Nf段曲线演化规律一致，相差幅度较小，但在其他段模型曲线与试验曲线相差幅度较大，均位于试验曲线下方。YLS模型函数为幂函数，其吻合程度相对前者较好，图3(a)的吻合程度较差，图3(b)、(c)、(d)、(e)所示，在0.10～1.00Nf段模型曲线与试验曲线变化规律大体一致，但在增减幅度上有一定的差异。图3(b)、(c)、(d)、(e)的试验曲线在寿命初期较短时间段内出现了先增长的趋势，而两种模型曲线并无先增长的趋势。

从以上拟合结果看出：(1)YLS、EEB模型为FRP层合板静态条件下的剩余刚度与寿命关联模型，试验结果为动态剩余刚度与寿命的关系，虽然在模型适用上存在一定差异，但当应力水平S=0.3、0.5时，YLS模型能较好应用于GFRP筋动态剩余刚度的退化分析；当S=0.6时，YLS、EEB模型均不适用动态剩余刚度退化分析;(2)GFRP筋疲劳损伤演变存在着较强的阶段性规律，动态剩余刚度的退化规律亦是如此，从模型角度而言，仅用一个表达式囊括其整个寿命周期的演化规律较难实现;(3)结合试验曲线规律，采用指数函数对GFRP筋动态剩余刚度和寿命周期之间的关系分段拟合，拟合曲线能体现试验曲线规律，如图3所示。图3(a)、(b)中，以0.1Nf内一点为分段界限，分别拟合收敛得到整个寿命周期的试验拟合曲线。拟合结果表明，指数函数表征此试验数据是合理的，拟合优度高、效果好。

3 结论

(1)在较小应力水平(S=0.3)、中等应力比(R=0.5)条件下，试件尺寸对疲劳性能影响较小，呈现相同的规律；在中等应力水平(S=0.5)、中等应力比(R=0.5)条件下，不同直径呈现不同的变化规律，直径16 mm与20 mm筋体的刚度退化明显不同;

(2)应力水平较大疲劳加载时，试样的刚度退化较严重，较大应力水平对筋体的疲劳寿命影响更显著;

(3)YLS模型在应力水平S=0.3、0.5时在寿命初期(0.1Nf)与实际情况吻合不佳，其他寿命周期内能较好表征GFRP筋体的疲劳损伤特性;采用分段指数函数拟合曲线能更好表征试验中的疲劳损伤特性;

(4)用动态剩余刚度与寿命比关系曲线来评价GFRP筋体在疲劳荷载作用下的损伤是可行的;

(5)部分GFRP筋动态刚度退化规律与FRP层合板刚度退化三阶段规律相似，而另外一部分筋体在加载初期阶段(0.1Nf)出现动态刚度先迅速增长的现象;这一阶段的现象还需要从应力水平和应力比上开展大量样本试验研究。

参考文献：

[1] VALLONS K, ZONG M, LOMOV S V. Carbon Compo-sites Based on Multi-Axial Multi-Ply Stitched Preforms-Part 6. Fatigue Behaviour At Low Loads: Stiffness Degradation and Damage Development[J]. Composites Part A, 2007,38(7):1 633-1 645.

[2] 宗俊达, 姚卫星. FRP复合材料剩余刚度退化复合模型[J]. 复合材料学报, 2016,33(2):280-286.

ZONG J D,YAO W X.Compound Model of Residual Stiffness Degradation for FRP Composites[J]. Acta Materiae Compositae Sinica,2016,33(2):280-286.

[3] SHIRI S, POURGOL-MOHAMMAD M, Yazdani M. Effect of Strength Dispersion on Fatigue Life Prediction of Composites under Two-Stage Loading[J]. Materials & Design, 2014,65:1 189-1 195.

[4] ELIOPOULOS E N, PHILIPPIDIS T P. A Progressive Damage Simulation Algorithm for GFRP Composites Under Cyclic Loading. Part I: Material Constitutive Model[J]. Composites Science & Technology, 2011,71(5):742-749.

[5] 王成华, 杨 阳, 康 强, 等. 一种新型刚度退化模型及复合材料结构渐进损伤分析的通用方法实现[J]. 工程力学, 2016,33(4):17-23.

WANG C H,YANG Y,KANG Q, et al. A Stiffness Degradation Model and A General Method for Progressive Failure Analysis of Composite Structures[J].Engineering Mechanic,2016,33(4):17-23.

[6] 张承承, 王建军. 基于刚度退化的复合材料结构损伤研究进展[J]. 材料导报, 2016,30(21):8-13.

ZHANG C C,WANG J J. Research Advances in Damage of Composite Structures on Stiffness Degradation[J].Materials Review,2016,30(21):8-13.

[7] 沈浩杰, 姚卫星, 吴富强. 复合材料刚度性能表征的协同损伤力学模型[J]. 力学学报, 2014,46(2):255-263.

SHEN H J,YAO W X,WU F Q. Synergistic Damage Mechanic Model for Stiffness Properties of Composite Laminates[J].Chinese Journal of Theoretical and Applied Mechanics,2014,46(2):255-263.

[8] 孙志刚. 碳纤维预应力筋及拉索锚固系统抗疲劳性能的试验研究[D]. 长沙: 湖南大学, 2005.

[9] 张新越, 欧进萍. CFRP筋的疲劳性能[J]. 材料研究学报, 2006,20(6):565-570.

ZHANG X Y,OU J P. Experimental Study on Fatigue Behavior of CFRP Bars[J].Chinese Journal of Materials Research,2006,20(6):565-570.

[10] Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials: ASTM I. D3039/D3039M-14[S]. West Conshohocken: 2014.

[11] Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials: ASTM I. D3479/D3479M-12[S]. West Conshohocken: 2012.

[12] RAMESH T. Fatigue of Composite Materials[M]. Lancaster: Technomic Publishing Company, 1987.

[13] REIFSNIDER K L, HENNEKE E G, Stinchcomb W W, et al. Damage Mechanism and NDE of Composite Laminates[M]. New York: Pergamon Press, 1983.

[14] YANG J N, JONES D L, YANG S H, et al. A Stiffness Degradation Model for Graphite/Epoxy Laminates[J]. Journal of Composite Materials, 1990,24(7):753-769.

[15] YANG J N, LEE L J, SHEU D Y. Modulus Reduction and Fatigue Damage of Matrix Dominated Composite Laminates[J]. Composite Structures, 1992,21(2):91-100.

[16] ECHTERMEYER A T, ENGH B, BUENE L. Lifetime and Young ’s Modulus Changes of Glass/Phenolic and Glass/Polyester Composites Under Fatigue[J]. Compo-sites, 1995,26(1):10-16.