圆锥破碎机性能模型研究综述

俞 安,于向军,刘 刚,张 威

(1.昆明学院 自动控制与机械工程学院,昆明 650214; 2.北方重工集团有限公司,沈阳 110141;3.吉林大学 机械科学与工程学院,长春 130022)

随着我国各项建设的不断推进,建筑、道路、矿业等工程行业对于物料的碎磨处理需求也以几何级数速度增长.在当前国内外所倡导的“多碎少磨” “以碎代磨”大趋势下,圆锥破碎机因其破碎原理先进、运行可靠、高效节能等特点备受广大生产厂商及用户青睐[1].圆锥破碎机破碎性能的优劣则直接决定其工作效率、能耗情况、市场竞争力等诸多方面,因此寻找并建立合理有效的性能模型，对于圆锥破碎机的设计、研发、维护具有至关重要的作用及意义.

目前圆锥破碎机性能模型主要包含3类:尺寸缩减模型、流动模型以及磨损模型[2].性能模型不仅用于指导圆锥破碎机的设计,而且对于推进性能表征参数的相关研究也具有极为重要的意义.性能模型用途如图1所示.本文对圆锥破碎机3大性能模型的研究进行分析,并结合国内外相关研究进展以及发展趋势，提出了在未来研究中需要解决的问题.

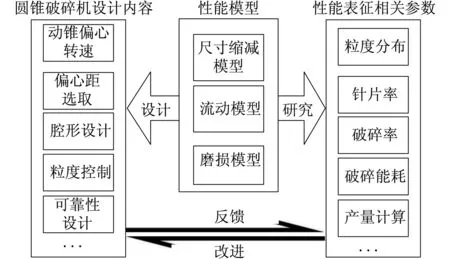
图1 性能模型用途Fig.1 The use of the performance model

1 圆锥破碎机性能模型

1.1 尺寸缩减模型

颗粒的尺寸缩减量是进行粒度分布估算、破碎率计算、产量评估等性能设计的重要指标.对于尺寸缩减模型的研究,单颗粒破碎是由于颗粒直接受作用于衬板,其发生条件是颗粒尺寸和动锥与破碎壁之间的距离相等或相近.有学者[3]对霍普金森压杆加以改进,通过实验观察单颗粒破碎过程,并给出了单颗粒破碎抗压强度及其损伤量的测量方法.然而圆锥破碎机实际作业过程中,并不仅仅出现单颗粒破碎一种机制,对于会出现“料床”的破碎设备,破碎过程同时伴随了大量的颗粒间作用,单颗粒破碎下的尺寸缩减模型对此无法进行有效描述.针对这一情况,Liu等[4]提出“层压破碎”概念,发生层压破碎的前提条件为颗粒与周围其他颗粒具有共同接触点,在颗粒崩碎时,这些接触点间的摩擦挤压促使更多破碎颗粒的产生.当入料颗粒尺寸小于排料口时,层压破碎则是一种非常重要的磨碎形式.多液压缸(高能)圆锥破碎机由于采用了层压破碎机制,其处理能力、破碎比以及动锥磨损均匀度等方面优于单缸圆锥破碎机.Evertsson等[5]建立了圆锥破碎机层压破碎过程中颗粒的尺寸缩减量数学模型:

pi=[BiSi+(I-Si)]pi-1

(1)

式中:Bi为颗粒破碎方式矩阵算子;Si为颗粒破碎概率矩阵算子.

在确定颗粒材料属性前提下,Bi,Si与无量纲参数压缩比以及颗粒在破碎腔中的位置有关.模型中通过破碎函数以及选择函数对层压破碎的描述较为理想,在此基础上加入单颗粒破碎机制,颗粒缩减模型得以进一步完善[6-7]:

(2)

(3)

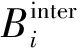
粒子粘合模型(the Bonded Particle Model)可以较好地体现颗粒破碎形态多样性,并且各个颗粒具备连续破碎能力,为离散元仿真分析模拟提取粒度分布以及产量值等数据提供了条件.由于物料颗粒的尺寸、形状不规则性,有必要将粘合模型中的球体粒子替换为非球体粒子[2,8],并通过落锤实验对模型颗粒破碎性质进行实证校准[9].因此在颗粒缩减模型研究过程中引入离散元素法,将有助于尺寸缩减模型在面向不同破碎对象时的处理能力.

1.2 流动模型

流动模型的发展是基于运动方程,通过3种运动机制来描述物料在破碎腔内的运动过程,分别为滑落、坠落以及坠落与滑动,如图2所示.当颗粒接触衬板时向下滑落,当衬板离开的加速度足够大时,颗粒发生坠落直至颗粒追赶上衬板并与其撞击.假设当颗粒接触到破碎壁表面并且衬板靠近时立即静止,在接下来挤压作用下颗粒发生破碎.

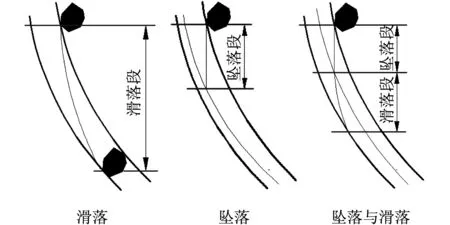
图2 颗粒的3种运动状态Fig.2 Three states of motion of particles

Eversson流动模型中的假设本质上规定破碎是在规定的自限机制条件下发生的.自限状态发生时颗粒相对于破碎壁表面静止.由于忽略了颗粒间的作用,对于假设的合理性有待考究.在实验观察中，发现圆锥破碎机工作过程中类似自限现象真实存在:物料颗粒在某一破碎带区间内出现停滞,阻碍上层物料下落并且出现带动上层物料反向抬升的趋势.经过进一步观察发现停滞带多位于轧臼壁与动锥衬板横截面最小间距所处水平面——阻塞点水平截面(the Choke Level)[10],如图3所示.

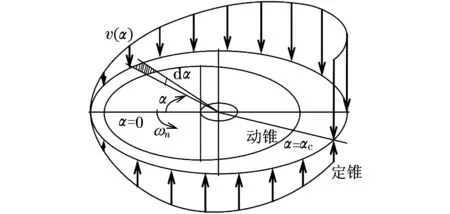
图3 阻塞点水平截面Fig.3 Horizontal section of the choke level

阻塞点水平截面将物料运动分为了上升、下落两类,且该面上两类运动同时存在,在已知物料填充密度的情况下，即可对图3中v(α)进行积分，阻塞点水平截面处对应单位时间参与两类运动的物料量[10]:

(4)

(5)

Rmin≤R(α)≤Rmax

式中:α为动锥摆角;ρ为阻塞点水平截面处沿α方向的物料密度;r为阻塞点水平截面处物料堆积带半径;Ri(α)为运动的物料以速度v(α)运动时到圆心的距离;R0为图中外圆半径;ac为物料处于下落阶段期间动锥转过角度.

将式(4)和式(5)对应参与两类运动的物料量相减，即可得到破碎机生产率Q:

Q=Qdown-Qup

(6)

新模型对粒度分布、颗粒堆积密度估算更加准确,阻塞点水平截面概念可以用于指导腔形设计以及动锥偏心速度优化，以提高效率、产量,但对系统动态特性、颗粒形态、颗粒流动速度和方向的影响考虑不充分,而过多条件的加入使得问题变得复杂,数学描述变得困难.有学者[9]转而通过离散元素法模拟颗粒下落过程,其结果能够较好地描述颗粒运动状态,但由于颗粒与衬板间的接触特性不明确，导致仿真结果与实验结果匹配度较低.

1.3 磨损模型

在1.2节介绍的3种运动状态下，颗粒对衬板会产生冲击、摩擦、挤压作用,而在上述综合作用下衬板的磨损较为迅速,导致破碎腔腔形出现变化，并且工啮角逐渐增大,进而导致粒度分布波动并降低破碎效率.因此有必要通过建立磨损模型，对衬板磨损机理进行描述.文献[11]介绍了一类适用于破碎机设计的磨损模型(Archard磨损模型)为

(7)

式中:W为磨损量;K为耐磨系数;s为滑动距离;p为外部载荷;pm为流动压力.

式(7)中考虑了导致磨损的两大因素:压力作用以及相对运动,并反映出磨损量与滑动距离以及压力成比例关系.而由于物料在轧臼壁以及破碎壁挤压、摩擦作用下发生了破碎,为耐磨系数K的确定带来困难.针对这一情况,有学者[12-13]通过反复试验，成功得到耐磨系数K,并且观察到了单颗粒破碎时衬板表面的微观破坏.Kivikytö-Reponen等[14]进一步利用全尺寸圆锥破碎机开展实验,得到衬板磨损行为与微观结构参数之间的联系:衬板材料的硬质相体积分数以及硬质相类型是影响磨损量的两个重要参数,并且即使物料与衬板间没有微观滑动,却依然观察到了磨损.Archard磨损模型显然与这一结果相悖.为了解释这一现象,Lindqvist等[15]对Archard磨损模型进行了改进,得

(8)

(9)

式中:W1,W2为结合衬板材料和耐磨度确定的材料参数;v为滑动速度.

式(8)为包含滑动、挤压复合作用的独立方程,式(9)为只有挤压作用下的独立方程.Lindqvist等[15]认为磨损量与破碎过程中出现的最大平均压力有关,式(9)考虑了无滑动情况下的磨损,却忽略了时间与磨损量之间的关系,Ma等[16]通过引入时间、破碎带压力等因素对磨损模型进一步改进,得

(10)

式中:Wi(t)为t小时后第i个破碎带的磨损量;Fn,i为第i个破碎带的压力;Fs,i为第i个破碎带的剪应力;Fn,p为第闭口附近第i个破碎带内的压力;Fs,p为第闭口附近第i个破碎带内的剪应力;Q为无滑动时剪切力影响下的模型参数;μ为衬板材料对应单位时间磨损率;m(t)为物料质量.

磨损量的新模型包含了时间变量对磨损量的影响,并且可以通过局部计算得到磨损分布形式.

2 未来发展趋势及待解决的问题

2.1 未来发展趋势

目前我国生产的破碎设备主要以低端产品为主,普遍存在着“高端不足,低端过剩”的现象.在我国产业结构调整期间,破碎行业面临着行业转型升级.对于圆锥破碎机,未来发展趋势可以概括为大型化、高效化、节能降耗以及绿色发展4个方面.产品的改进、升级、创新离不开理论支撑,而由于圆锥破碎机测试，实验成本较高,所以有必要充分结合计算机仿真技术对性能模型加以完善.

2.2 待解决的问题

关于圆锥破碎机性能模型的研究目前主要存在以下几方面问题:

(1) 多粒径表征指标的确定.目前尺寸缩减模型还无法有效描述物料尺寸缩减过程中出现的各种尺寸以及形态,寻找并确定多粒径表征指标，有助于针片率以及粒度分布的精确计算.

(2) 实验与仿真的规范、标准制定.近些年越来越多的学者通过仿真分析建立性能分析模型,配合加压床实验、落锤实验等，确定物料压缩比、接触特性可以大大提高性能模型的适应性、有效性以及准确性,然而由于缺少相关实验与仿真的规范及标准,状态标定与校准不统一,导致仿真结果间差异较大,从而严重影响结果的准确性、有效性以及可靠性.

(3) 性能模型适应性的提高.目前在已知物料破碎前的入料分布及其材料物理属性的前提下,利用性能模型已经可以实现对圆锥破碎机性能的最优化设计,而在实际生产过程中破碎对象的质地属性往往不同,导致优化效果不理想,有必要对性能模型进行完善以提高其对各类破碎对象的适应性及实用性,其中仿真分析的应用将大大提高模型分析效率,有助于性能模型的发展以及推广.

(4) 产量模型的改进.根据流动模型得到生产率计算方程,由于忽略了对于物料与衬板的摩擦作用，以及颗粒破碎时的能量释放对颗粒下落的影响,推导出的产量与实际测试结果误差较大.

(5) 机体质量优化.在“大型化”趋势下,机体质量将直接关系到设备制造加工、运输、安装、维修难度及成本.目前国内由于对产品性能设计经验欠缺,导致在结构优化过程中，对关键部位往往采取过于保守的约束条件,导致减重效果不理想,与国外同规格产品机重控制差距较大.因此有必要发展并完善性能模型,在优化过程中引入性能模型中的性能参数,实施机重的多目标优化策略,将有助于指导结构优化，从而进一步有效降低机体质量.

参考文献:

[1] WALKER S.Cone crushers:the suppliers’ perspective[J].Engineering and Mining Journal,2011,212(5):54-61.

[2] LI H.Discrete element method(DEM)modelling of rock flow and breakage within a cone crusher[D].Nottingham:University of Nottingham,2013：32-43.

[3] PRASHER C L.Crushing and grinding process handbook[M].New Jersey:John Wiley and Sons Ltd,1987:46-49.

[4] LIU J,SCHÖNERT K.Modelling of interparticle breakage[J].Intemational Journal of Mineral Processing,1996,44(3):101-115.

[5] EVERTSSON C M,BEARMAN R A.Investigation of interparticle breakage as applied to cone crushing[J].Minerals Engineering,1997,10(2):199-214.

[6] 马彦军,范秀敏,何其昌,等.圆锥破碎机破碎质量的粒度和粒形数学建模[J].机械工程学报,2013,49(6):95-102.

MA Y J,FAN X M,HE Q C,et al.Mathematical modeling of particle size and particle shape of crushing quality for cone crusher[J].Journal of Mechanical Engineering,2013,49(6):95-102.

[7] 张子龙,任廷志,程加远,等.考虑粒形转化特性的圆锥破碎机层压破碎行为研究[J].机械工程学报,2017,53(16):173-180.

ZHANG Z L,REN Y Z,CHENG J Y,et al.Research on the inter-particle breakage of cone crusher considering the characteristics of particle shape transformation[J].Journal of Mechanical Engineering,2017,53(16):173-180.

[8] DELANEY G W,MORRISON R D,SINNOTT M D,et al.DEM modelling of non-spherical particle breakage and flow in an industrial scale cone crusher[J].Minerals Engineering,2015,74:112-122.

[9] JOHANSSON M,QUIST J,EVERTSSON M,et al.Cone crusher performance evaluation using DEM simulations and laboratory experiments for model validation[J].Minerals Engineering,2017(1):93-103.

[10] EVERTSSON C M.Modelling of flow in cone crushers[J].Minerals Engineering,1999,12(12):1479-1499.

[11] SHEN F,HU W,VOYIADJIS G Z,et al.Effects of fatigue damage and wear on fretting fatigue under partial slip condition[J].Wear,2015,338/339:394-405.

[12] 李永堂,付建华,雷步芳,等.多元低合金耐磨钢破碎机衬板制造工艺研究[J].机械工程学报,2013,49(12):72-77.

LI Y T,FU J H,LEI B F,et al.Research on manufacturing process for complex low-alloyed wear-resisting crusher liner[J].Journal of Mechanical Engineering,2013,49(12):72-77.

[13] YAO M,PAGE N.Friction measurement on Ni-Hard 4 during high pressure crushing of silica[J].Wear,2001,249:117-126.

[14] KIVIKYTÖ-REPONEN P,ALA-KLEME S,HELLMAN J,et al.The correlation of material characteristics and wear in a laboratory scale cone crusher[J].Wear,2009,267:568-575.

[15] LINDQVIST M,EVERTSSON C M.Improved flow-and pressure model for cone crushers[J].Miner Eng,2004(17):1217-1225.

[16] MA Y,FAN X,HE Q.Prediction of cone crusher performance considering liner wear[J].Applied Sciences,2016,6(12):404.