最小二乘配置法优化的REHSM模型及应用

王东东，张 俊，邓小东，刘继庚，赵旭坤

(贵州大学矿业学院，贵州 贵阳 550025)

自板块构造运动理论提出以来，很多学者根据地球物理资料，基于欧拉定理，建立了一批全球板块运动模型[1-3]。这些早期的模型大多是将板块运动看作是一种刚性运动，认为板块运动时，其内部不发生变形，或者认为变形只发生在板块边缘一定条带范围。20世纪90年代以来，有关研究已经发现，板块边缘是发散的，板块具有弹塑性。地球物理学也表明，一点的运动或多或少都具有一定的弹性性质和塑性性质[1]，并且地球的岩石圈在几年到几十年的时间尺度上，表现为弹性性质，在这个时间尺度上进行研究，可以将块体视为弹性介质[4]。目前，大地测量技术可在几千千米的空间尺度中实现对地表位移的监测，精度达到毫米级[5]，可以精确地监测板块运动状况，使研究板内形变成为可能。一个板块受周围板块的作用常常发生板内形变，板内形变长期积累是地震发生的原因[6]，因此，研究板内形变，对于研究地震的发震机制具有很强的现实意义。李延兴等学者建立了板块的整体旋转与均匀应变模型(REHSM)[7]和整体旋转与线性应变模型(RELSM)[4]，对板块旋转参数和板内应变参数进行了统一解算，改变了以往两种参数分开解算的状态，它们是真正意义上的综合模型。由于顾及了板内形变，这两种模型对地壳运动的速度场拟合精度明显优于刚性运动模型[4]。但鉴于不同区域地质构造环境的差异和复杂性，简单假设板内形变应变随位置呈均匀或线性变化，可能与实际板块运动难以达到最佳的符合。为此，本文提出一种利用最小二乘配置模型(LSC)对REHSM模型进行优化的方案，即仍然假定板内各点的形变应变随位置大致呈均匀变化，但同时认为板块运动除遵循整体刚性旋转运动和均匀应变外，还存在板内非均匀应变。由于非均匀应变量级和形式都非常复杂，并受许多地质构造因素影响，故可利用LSC模型中的信号部分对偏离均匀应变的部分进行补偿，而将REHSM模型表达为LSC的主项，即趋势项，以此建立板块运动及形变模型，称为〗LSCREHSM模型。对最近几期中国大陆构造环境监测网络在环渤海区域的速度场数据进行拟合分析，结果表明LSCREHSM模型可以精确描述块体的整体运动和板内应变情况，其拟合结果明显优于REHSM模型。

1 刚性运动模型

传统板块构造理论认为板块是一个刚体，其运动模型为

(1)

式中，VE、VN分别为板块上任意一点在东西方向和南北方向的运动速率；λ、φ为经纬度；ωx、ωy、ωz为欧拉旋转参数；r为地球平均半径。

2 块体运动的整体旋转与均匀应变模型

在研究大范围的块体运动与应变时，常采用球面坐标系。以块体的几何中心(λ0，φ0)为坐标原点，以纬线为x轴、经线为y轴建立球面坐标系。其中，令块体上一点沿纬线到y轴的平行圈弧长为x坐标，沿经线到x轴的子午圈弧长为y坐标，则有

(2)

一个块体受到周围块体的碰撞和挤压，会使块体发生整体旋转和板内形变。以往大多数建立的是块体的刚性运动模型，认为形变只发生在块体的边缘，忽略了板内形变，这与块体的实际运动情况不符。大地测量技术得到的块体运动速率是块体整体运动和局部板内形变的综合。利用GPS速度场数据建立块体的刚性运动模型，不能描述板内形变情况。李延兴给出了顾及板内形变的块体运动模型，将块体的整体旋转和板内应变统一起来进行参数求解。当假设板内的应变是均匀变化的，其模型为

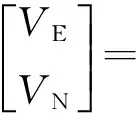
(3)

式中，εE、εEN、εN为应变参数；其他参数含义同式(1)、式(2)。

3 块体运动的整体旋转与线性应变模型

若进一步假设块体内部的形变是线性应变，则可得到块体的整体旋转与线性应变模型，其模型为

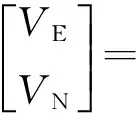
(4)

式中，第一项参数同式(1)；A0、B0、C0、A1、B1、C1、A2、B2、C2为应变参数。

4 最小二乘配置模型

最小二乘配置模型的一般形式为[5]

L=AX+Y+Δ

(5)

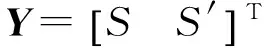
通过间接平差得到参数为

(6)

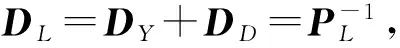
已测点和未测点的估值为

(7)

式中，Ds为已测点协方差阵；DS′S为已测点和未测点之间的协方差阵。

最小二乘配置的核心是协方差函数的确定和拟合，选择合适的协方差函数是得到最优结果的保障。许多学者在板块运动中使用LSC模型时，常常选择高斯指数函数作为协方差函数模型，并取得了良好的结果[5，8-13]，详见文献[11]。

5 块体运动的LSCREHSM模型

空间大地测量技术得到的数据是块体的整体运动与板内形变的综合，其中必然包含扩张形变的影响[14]。REHSM假设块体内部形变是均匀应变，而这种扩张形变必然会影响板内应变，破坏其对板内形变的均匀应变的假设，在块体运动活跃区域将会表现得更加明显。这种情况下建立的模型既不能精确描述块体的整体旋转运动，也不能精确描述板内形变情况。因此，采用最小二乘配置模型中的信号部分来描述板内应变偏离均匀应变的部分，从而建立一种改进模型，其形式为

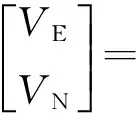
(8)

6 环渤海区域地壳形变分析

本文采用中国大陆构造环境监测网络在环渤海区域的GPS观测速度场数据。监测站空间分布范围为30.96°N—42.54°N、111.48°E—128.11°E，共有482个监测站，其中包括基准站32个，区域站450个。基准站数据采集时间为2010—2014年；区域站数据采集时间为2009年、2011年和2014年3期观测数据，每个测站连续观测3 d，采样间隔为30 s。通过对监测站观测资料的处理，得到环渤海区域统一速度场数据，精度优于2 mm/a。

鉴于块体运动整体上具有长期稳定性，其主要规律应遵循欧拉刚体整体旋转运动规律，为此，需要对明显偏离块体整体运动趋势的测站进行剔除。具体做法为：利用式(1)计算块体在东方向和北方向运动速率的残差，以块体测站速率分量标准差平均值的2倍作为选站的限差，逐步剔除那些明显偏离块体整体运动趋势的测站，直至剩余测站的速率残差绝对值均小于限差为止。经过以上方法对环渤海482个测站进行筛选，共剔除测站48个。

为验证本文方法，分别采用RRM、REHSM、RELSM和LSCREHSM这4种模型及拟合方案对环渤海区域GPS速度场进行拟合分析，结果列于表1，同时给出了4种模型解算的速度残差图，如图1所示。表中SΔv利用式(9)计算。

(9)

式中，ΔvEi、ΔvNi分别为块体第i个测站在东西方向和南北方向运动速率的残差；R为未知参数的个数；n为测站个数。

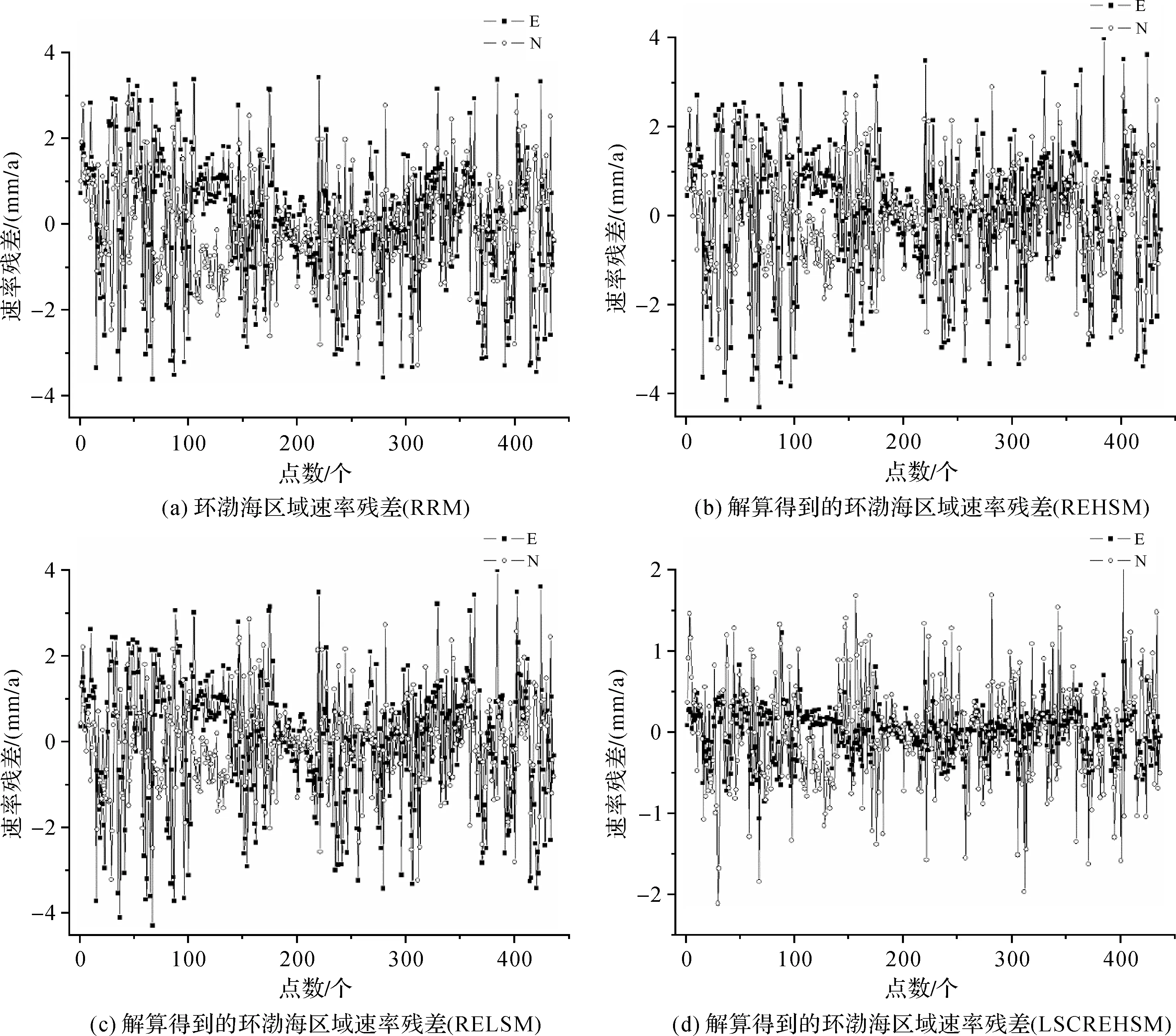
图1

块体名称模型欧拉运动参数λ/(°)φ/(°)ω/(°)速率残差标准差SΔv/(mm/a)环渤海区域RRM-127.0±3.3370.6±0.830.332±0.0041.32REHSM-120.8±2.9868.8±1.000.324±0.0041.28RELSM-119.6±3.3668.2±1.270.322±0.0051.28LSCREHSM52.1±0.00257.4±0.0020.11±0.00000.49

对计算结果进行分析如下：

(1) 从图1(a)—(c)可以看出，块体在东西方向和南北方向运动速率的残差均在4.5 mm以内，且图1(a)速率残差的波动要略微大于图1(b)和图1(c)；图1(b)和图1(c)中速率残差的波动相似；由图1(d)也可以看出，在东西方向和南北方向的运动速率残差均小于2.5 mm/a，表明了4种模型在描述板块长期趋势性运动都是有效的。从4种模型解算的运动速率残差可以得出，LSCREHSM模型拟合的效果明显优于其他3种模型。

(2) 从表1可以看出，RRM模型处理的效果最差，由于RRM模型只考虑到块体的整体旋转运动，没有顾及板块内部形变，其处理效果最差是可以预见的；REHSM模型和RELSM模型分别假设板内应变是均匀和线性的，其数据处理结果的精度相当，均优于RRM模型处理的结果，说明假设具有一定的合理性。

(3) 从表1也可以看出，LSCREHSM模型解算的效果优于REHSM模型和RELSM模型。这是因为环渤海区域块体运动活跃，呈现扩张状态，且有部分区域是陆地和海洋相接，其地质情况复杂[15]，在该区域对板内运动情况作任何假设都难以符合实际情况。在环渤海区域，假设板内应变是均匀应变或线性应变，显然很难描述板内实际应变状态。

(4) 本文假设板内应变以均匀应变为主，其次板内还存在偏离均匀应变的其他应变，将其看作信号。采用LSC模型对信号加以描述，试验结果表明LSC模型对偏离均匀应变的部分，处理是有效的，得到的结果更加符合本区域块体运动的实际情况。说明该模型不仅可以精确描述块体的整体旋转运动，而且还可以精确描述块体内部应变情况。

7 结 语

RRM模型仅能描述块体长期运动的平均趋势性运动，不能顾及板内形变。REHSM和RELSM模型虽然顾及了块体的内部形变，但这两种模型分别假设块体内部形变为均匀应变和线性应变，仍然具有相当的局限性。本文提出利用LSC中信号对偏离REHSM的板内形变进行补偿，建立了LSCREHSM地壳形变分析模型，取得了良好的效果，为地壳形变分析提供了一种新的思路。

利用LSCREHSM模型进行地壳形变分析涉及协方差函数的构建，协方差函数的好坏将直接影响形变分析结果。本文采用高斯指数函数进行协方差函数拟合，取得了较好的结果。说明假定地壳运动速度场各点间的联系随距离衰减是基本符合实际的。但在不同区域，因地质构造情况差异性较大，LSCREHSM模型的适用性尚需进一步验证。

参考文献：

[1] JIN S，ZHU W.A Revision of the Parameters of the NNR-NUVEL-1A Plate Velocity Model[J].Journal of Geodynamics，2004，38(1):85-92.

[2] DEMETS C，GORDON R G，ARGUS D F，et al.Current Plate Motions[J].Geophysical Journal International，1990，101(2):425-478.

[3] ARGUS D F，GORDON R G.No-net-rotation Model of Current Plate Velocities Incorporating Plate Motion Model NUVEL-1[J].Geophysical Research Letters，1991，18(11):2039-2042.

[4] 李延兴,张静华,何建坤,等.由空间大地测量得到的太平洋板块现今构造运动与板内形变应变场[J].地球物理学报，2007，50(2)：437-447.

[5] 江在森,刘经南.应用最小二乘配置建立地壳运动速度场与应变场的方法[J].地球物理学报，2010，53(5)：1109-1117.

[6] BURBIDGE D R.Thin Plate Neotectonic Models of the Australian Plate[J].Journal of Geophysical Research Solid Earth，2004，109(B10):1-15.

[7] 李延兴,胡新康,帅平,等.中国大陆地壳水平运动速度场与应变场[J].国际地震动态，2002(7)：1-9.

[8] 杨元喜,曾安敏,吴富梅.基于欧拉矢量的中国大陆地壳水平运动自适应拟合推估模型[J].中国科学:地球科学，2011，41(8)：1116-1125.

[9] 张贵钢,杨志强,王庆良,等.基于最小二乘配置模型探讨青藏高原巴彦喀拉块体的运动特征[J].地球科学与环境学报，2011，32(2)：213-216.

[10] 张希,江在森.考虑区域构造特征的最小二乘配置方法初步研究[J].中国地震，2001，17(4)：78-82.

[11] 柴洪洲,崔岳,翟天增,等.中国大陆主要块体水平运动协方差函数确定方法研究[J].大地测量与地球动力学，2009，29(4)：74-78.

[12] 赵丽华,曾安敏.自适应拟合推估在地壳形变分析中的应用[J].大地测量与地球动力学，2009，29(1)：132-134.

[13] 柴洪洲，崔岳,明锋.最小二乘配置方法确定中国大陆主要块体运动模型[J].测绘学报，2009，38(1)：61-65.

[14] 李延兴,张静华,何建坤,等.菲律宾海板块的整体旋转线性应变模型与板内形变-应变场[J].地球物理学报，2006，49(5)：1339-1346.

[15] 李延兴,马宗晋,张静华,等.渤海盆地的现今扩张运动[J].地球物理学报，2009，52(6)：1483-1489.

[16] 丁阿鹿,杨建华,张莞玲,等.基于自适应拟合推估的最小二乘配置改进模型在地壳形变分析中的应用研究[J].测绘通报,2013(1):19-21.

[17] 曾安敏,刘光明,秦显平,等.应用拟合推估法建立我国大陆地壳水平运动速度场的研究[J].测绘通报,2012(S1):11-15.