多系统GNSS RTK的改进卡尔曼滤波算法

范红平，周志峰，王永泉

(1. 上海工程技术大学机械工程学院，上海 201620； 2. 上海司南卫星导航技术股份有限公司，上海 201801)

实时动态差分法(real-time kinematic,RTK)是基于载波相位观测值来提高GNSS位置数据精度的技术，而多系统GNSS RTK融合了GPS、GLONASS、BDS和Galileo的4大卫星导航系统的定位数据，提供更多的可见卫星，实现更高的RTK定位精度[1]。Kalman滤波应用于RTK是通过动态推导，不存储过去的观测数据，只根据新的数据和前一时刻的估计量，借助状态转移方程不断迭代，逐步实现预测位置收敛于实际位置坐标即稳态值[2]。多系统GNSS增加了可见卫星数，使状态向量的维数急剧增加，这导致Kalman滤波方程乘法次数增加[3]。研究学者对其进行了多方面改进，赵占祥等提出一种矩阵外积法减少乘法运算次数，同时避免了矩阵求逆，占原算法CPU 1/8的时间[4]；胡朱林引用平方根协方差滤波，实现Q-R矩阵分解的自适应滤波，证明其可行性[5]；郭树人等利用稀疏矩阵、矩阵对称性及其求逆降维等方法，提出了快速Kalman算法，降低了1/6的乘法运算复杂度，并且CPU耗时降至原算法的1/3左右[6]。以上方法均证实有效，但对矩阵计算方法不足。

本文利用状态变量解算每颗卫星的整周模糊度和电离层延时，利用卫星数目与矩阵维数成正比[7]，提出一个改进Kalman滤波计算方法，推导出稀疏状态转移矩阵F，并且对协方差矩阵分块求解，最后利用对称性减少n(n+1)/2次乘法(n为矩阵维数)，大幅缩短CPU运行时间。

1 GNSS RTK的Kalman滤波模型

1.1 线性高斯系统的Kalman滤波方程

建立以下Kalman滤波的系统动态方程，式(1)、式(2)为一步预测过程，得出下一时刻最优预测值[8]。式(3)、式(4)和式(5)为一步更新过程，先计算出卡尔曼增益K，然后计算状态估计值。

(1)

(2)

(3)

(4)

Qk,k=[1-KkHk]Qk,k-1

(5)

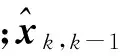
1.2 GNSS RTK的双差观测方程

假设用户接收机u和基准站接收机r同时跟踪卫星i和卫星j，则GNSS第k历元在L1和L2两个载波频率上双差载波相位和双差伪距的观测方程分别为

(6)

(7)

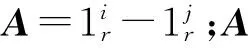
1.3 优化Kalman滤波运算的必要性

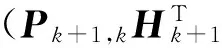
当前理想状态下，上海地区可见卫星数(高度角10°)为36颗(GPS、GLONASS、BDS和Galileo分别为12、8、12和4颗)，Kalman滤波方程的状态转移矩阵和协方差矩阵维数将达到117维[12]。仅一次迭代，式(2)的协方差矩阵的求解达到27 378次乘法，占用82 ms(32位系统一次乘法浮点运算占3 μs)。此外随可见卫星数的变化，Xk维数也随之变化，尤其当卫星数增加时，为保证滤波的连续性，应动态更新协方差阵Pk,k[13]。本文考虑以上因素，从两方面改进Kalman滤波方法。

2 改进型Kalman滤波方法

2.1 改进1：状态转移矩阵F模型

本文取三维直角坐标构建定常加速度动态模型，假设载体处于稳定加速状态，则状态参数需要增加3个加速度分量，则9+3i维状态变量为

(8)

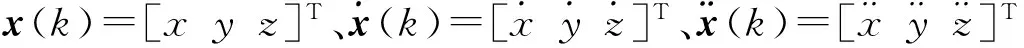
(9)

式中，τ表示k-1到k历元的时差；In为n维单位矩阵。

2.2 改进2：协方差矩阵Q计算

根据式(2)与式(8)，Qk,k为9+3i维矩阵[14]，可将其分为Q11、Q12、Q21和Q224块(阶数分别为9×9、9×3i、3i×9和3i×3i)，故Qk,k-1一步迭代计算

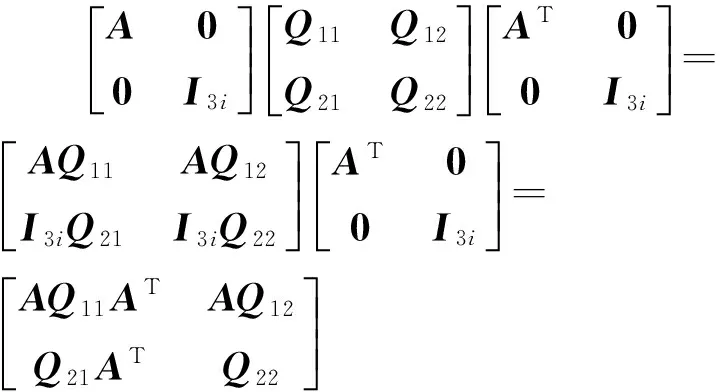
(10)

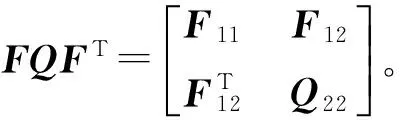
3 算例及分析

3.1 理论分析

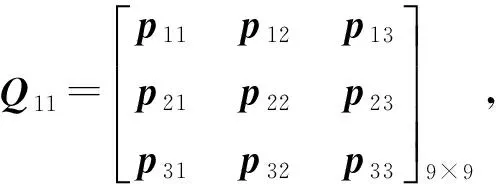
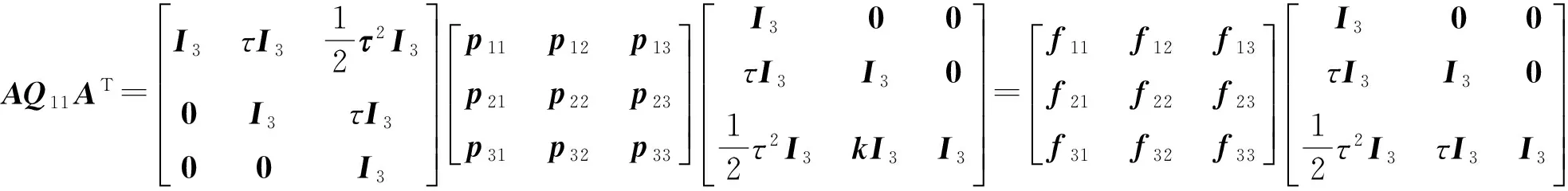
(11)

(12)

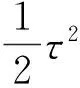
依据普通矩阵乘法[15]，Qk,k乘法次数为H2=2×(9+3i)3次， 以H1/H2百分比为纵坐标，卫星数为横坐标绘制柱状图如图1所示。

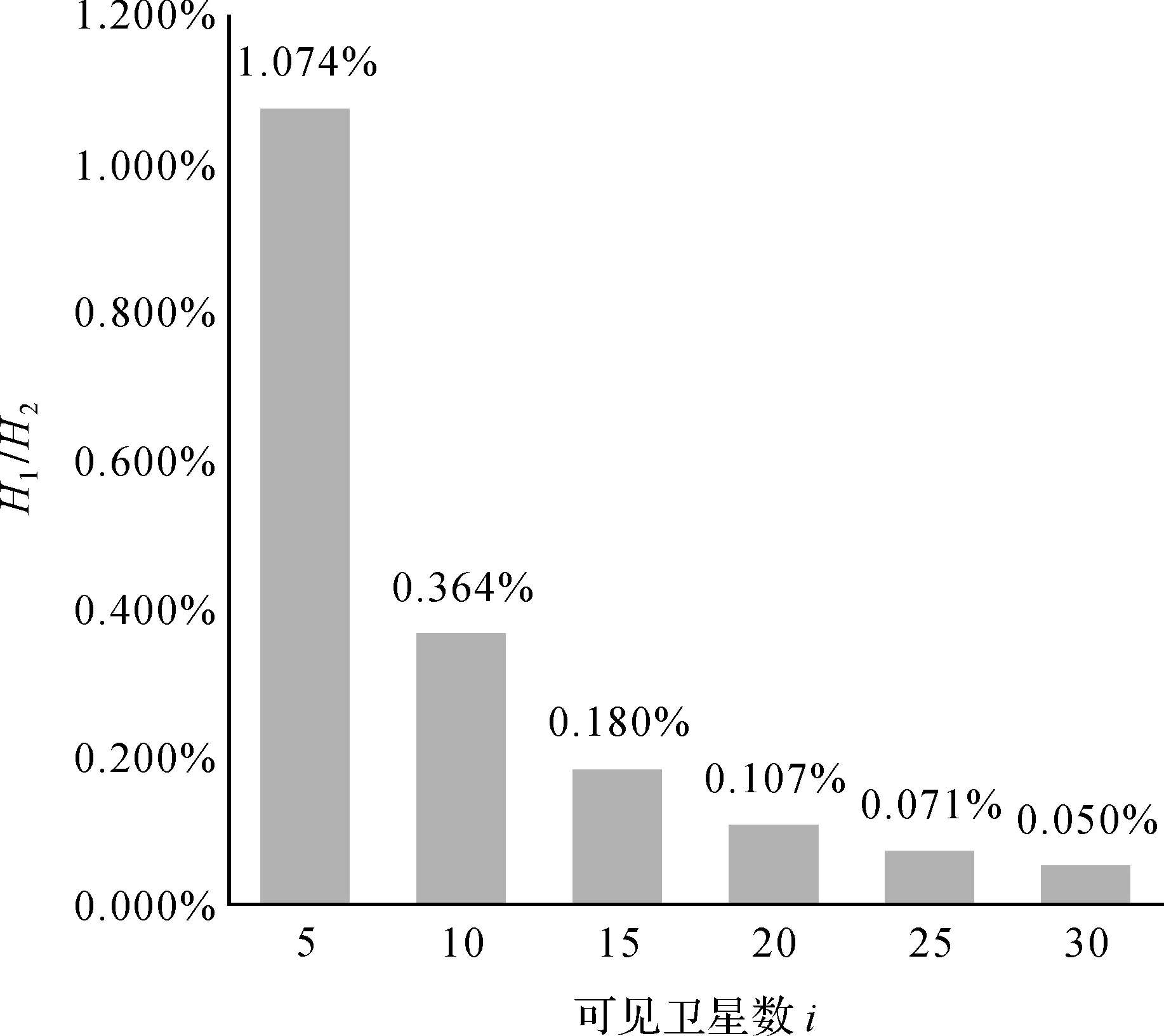
图1 改进算法优化比率

如图1所示，可见卫星多于4颗，其改进算法乘法次数H1均低于普通矩阵H2的1.2%，且随可见卫星数i增加，乘法次数提高到0.05%，达到了百倍的提升。

3.2 试验平台分析

为直观显示改进算法的特性，本次采用车载GNSS动态测量试验数据。2017年6月用3台SinoGNSS M600 GNSS接收机进行动态测量试验，如图2所示，其中一台接收机放置在基准站Location1，其他2号和3号放在速度为80 km/h的汽车车内(固定位置不变)。

图2 试验平台

本文采用CPU为2.9 GHz的联想计算机进行Matlab编程，对比两算法解算耗时分析。表1列出了不同的动态GNSS应用中，两算法的Kalman滤波循环一万次取平均值。

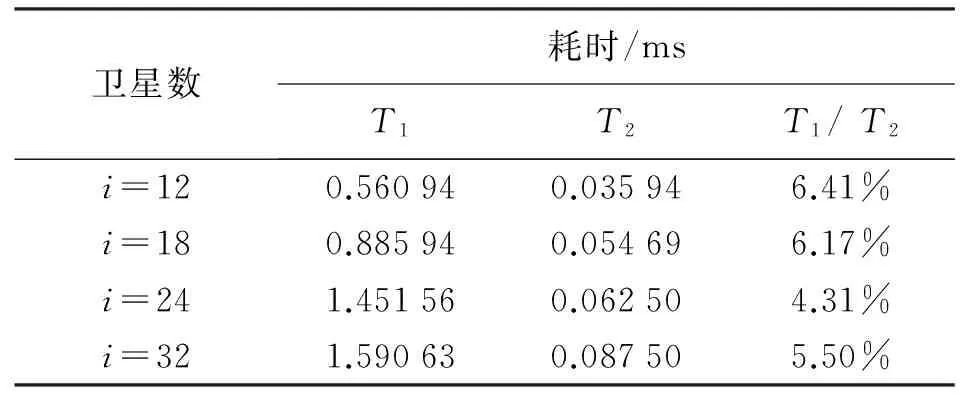
表1 不同参数下CPU运行时间

T1、T2分别代表普通算法和改进算法的Kalman滤波一次迭代所用时间，改进算法所用耗时均低于普通算法10%，最低可以达到4.31%。实际CPU处理器采用四级流水线技术，将几条指令并行处理，其对Kalman滤波算法总体上加快了指令流速度，缩短了程序执行时间，故实际Kalman滤波运算耗时高于一次迭代测量值T2/T1，故表1仅概略反应算法效率。

4 结 论

Kalman滤波迭代收敛过程中，经处理器的流水线技术处理，使实际计算耗时高于测量值。因此表1为估计数值，但可以确定CPU计算耗时低于普通算法的10%。该改进算法乘法次数降低到1%，故实现了算法的高效性。在动态GNSS数据处理中，通常Kalman滤波算法会采取适当优化，本文基于非优化算法求解双差整周模糊度，尤其在多系统产生的可见卫星数目增加情况下，有一定的参考价值。

致谢：上海司南卫星导航技术股份有限公司对本文的工作提供了试验平台和技术支持，在此表示衷心感谢。

参考文献：

[1] 任晓东,张柯柯,李星星,等.BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J].测绘学报,2015，44(12):1307-1313.

[2] MOURI A，KUBO Y，SUGIMOTO S.Detection and Correction of Doppler Biases in Kalman Filter-based Positioning[J].Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications,2015(10):156-164.

[3] WANG D，LV H，WU J.Augmented cubature Kalman Filter for Nonlinear RTK/MIMU Integrated Navigation with Non-additive Noise[J].Measurement，2017,97(2):111-125.

[4] 赵占祥,李兴国,娄国伟,等.矩阵外积法Kalman滤波器在动态GPS定位中的应用[J].火力与指挥控制,2006，31(4):27-29.

[5] 胡朱林.基于矩阵分解的卡尔曼滤波技术分析及应用[J].数字技术与应用,2016，(11):222.

[6] 郭树人,郭海荣,何海波,等.GPS动态数据处理中的快速Kalman滤波算法[J].测绘科学技术学报,2006,23(3):171-173.

[7] SAHMOUDI M，LANDRY R.A Nonlinear Filtering Approach for Robust Multi-GNSS RTK Positioning in Presence of Multipath and Ionospheric Delays[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):764-776.

[8] LI B，SHEN Y，FENG Y.GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J].Journal of Geodesy,2014,88(2):99-112.

[9] 孙红星,李德仁.使用双频相关法单历元解算GPS整周模糊值[J].测绘学报，2003,32(3):208-212.

[10] 董绪荣,陶大欣.一个快速Kalman滤波方法及其在GPS动态数据处理中的应用[J].测绘学报,1997(3):35-41.

[11] PROCHNIEWICZ D，SZPUNAR R，WALO J.A New Study of Describing the Reliability of GNSS Network RTK Positioning with the Use of Quality Indicators[J].Measurement Science and Technology,2017,28(1):12-15.

[12] 郭海荣,杨元喜,何海波,等.导航卫星原子钟Kalman滤波中噪声方差-协方差的确定[J].测绘学报,2010,39(2):146-150.

[13] Bartonek D，BURES J，SVABENSKY O.Optimization of Process Field Measurement GNSS-RTK for Railway Infrastructure[J].Solid State Phenomena，2017,25(8):481-484.

[14] PAZIEWSKI J，SIERADZKI R.Integrated GPS+BDS Instantaneous Medium Baseline RTK Positioning：Signal Analysis，Methodology and Performance Assessment[J].Advances in Space Research，2017，60(12):2561-2573.

[15] PAN V Y.Nearly Optimal Computations with Structured Matrices[J].Theoretical Computer Science，2017：953-962.