基于移动最小二乘法法矢估计的建筑物点云特征提取

裴书玉，杜 宁，王 莉，张春亢，刘继庚，徐光禹

(贵州大学矿业学院，贵州 贵阳 550025)

随着数字城市概念的提出和快速发展，大比例尺的三维城市模型成为近年来重建技术的研究热点[1-3]。三维激光扫描作为一种快速获取建筑物表面三维模型的新技术，能够提供丰富的关于建筑物立面的三维空间信息，如高精度的点云、RGB信息、反射强度及同轴相机拍摄的高清影像，从而为建筑物的重建研究提供了新的数据支持[4-6]。然而现实中建筑物结构的高度复杂性，给模型的重建工作特别是特征要素的提取工作带来了很大的麻烦。在整个建模周期中，特征要素的提取是最耗时的阶段，也是重建工作的灵魂，能否恢复具有高度真实感的模型，很大程度上取决于特征要素的恢复效果。因此，快速且准确地提取建筑物的特征要素显得极为重要。

在建筑物点云特征提取的研究中，针对不同的建筑物模型，相关学者提出了不同的特征提取算法。詹庆明等利用Hough变换和最小二乘法从古建筑点云中提取直线和圆，虽然精度较高，但提取的特征不够完整[7]。于海霞等针对立面基本垂直于地面、表面基本平滑、转角基本为直角的规则建筑物采用平面拟合算法提取特征点的方法，但对于结构复杂的建筑物模型并不适用[8]。杨林等提出影像辅助下的建筑物点云特征精细提取方法，该方法受影像与点云数据的配准误差、投影视差等误差的影响，且无法提取特征边缘存在曲线的特征[9]。陈朋等以点到其3个相邻邻域点所构成平面的距离平均值进行特征点的提取，点到平面的距离只能表征部分点的显著性而使得一些特征点不能被识别出来[10]。

针对上述问题，本文基于地面三维扫描的建筑物点云数据，提出一种建筑物点云特征提取方法，该方法首先采用移动最小二乘法进行法矢估计，然后将K邻域法矢夹角的均值作为点的显著性指标进行特征点判别，最后对特征点进行下采样得到清晰完整的特征线。

1 算法原理

1.1 移动最小二乘曲面

移动最小二乘法(moving-least square，MLS)是一种离散数据插值的方法，用其进行曲面拟合精度高，曲面表达简单[11]。基于移动最小二乘算法进行曲面拟合较传统最小二乘有两大改进：一是拟合函数的构建不同；二是引入紧支(compact support)概念。研究表明，最小二乘曲面拟合充分考虑了中心点的K邻域信息，且邻域大小可以根据不同模型进行调整，使散乱点云数据法矢估计更加准确和稳健[12]。故本文以基于投影的移动最小二乘曲面为基础进行法矢估计，将点的K近邻点拟合成局部二次曲面后得到该点的估计法矢。

1.1.1 拟合函数的建立

在局部区域内移动最小二乘拟合函数表示为

(1)

式中，α(x)=[α1(x)α2(x) …αm(x)]T为待求系数，它是坐标x的函数；p(x)=[p1(x)p2(x) …pm(x)]T，称为基函数，基函数p(x)是个k阶多项式，m为基函数的项数。线性和二次基的基函数分别为p(x)=[1xy]T和p(x)=[1xyx2xyy2]T。本文采用二次基以提高曲面拟合及法矢估计的精度。加权残差方程的表达式为

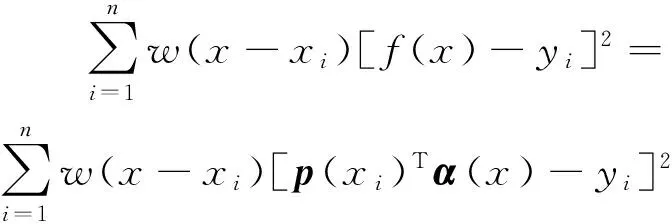
(2)

式中，w(x-xi)为节点xi的权函数。

为了求式(2)的系数α(x)，必须使其取极小值，即对α进行求导运算。求导后的计算结果为

(3)

式(3)经整理后可表示为

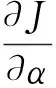
(4)

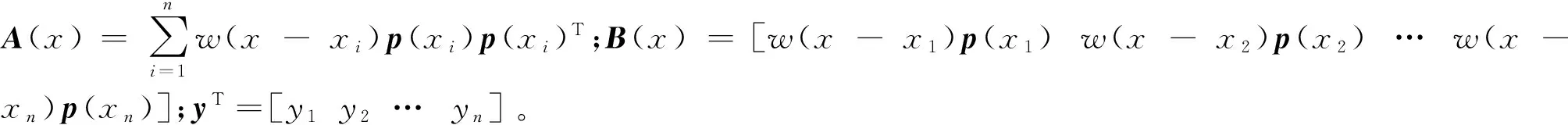
于是求得的拟合方程的系数为

α(x)=A-1(x)B(x)y

(5)

(6)

式中，φk(x)为形函数；k为基函数的阶次。

1.1.2 权函数

权函数作为控制移动最小二乘曲面特征拟合尺度的重要参数，其选取对拟合精度非常重要。移动最小二乘法中的权函数w(x-xi)应该具有紧支性，即权函数只受x周围一定区域内的影响，超出该区域后其权值很小，影响可以忽略，该区域称为权函数的影响区域。一般来说选择圆形作为权函数的支持域，其半径记为smax，如图1(a)所示。

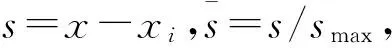
(7)

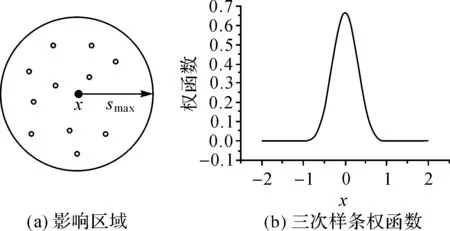
图1 影响区域和三次样条权函数

1.2 法矢计算及重定向

定义局部二次曲面为S(u,v)=S(u,v,h(u,v))则曲面在该点的一阶偏导计算公式为

(8)

其中，h(u,v)=au2+buv+cv2+du+ev+f。

故曲面在该点的法矢向量计算公式如下

(9)

式中，a、b、c、d、e、f为曲面方程系数。

移动最小二乘法计算出的法矢具有二义性，即只得到了法矢所在的直线，而没有确定以直线的哪个方向为法向量的最终方向。因此，需要为模型中点的法矢规定一个统一的方向，如所有法矢都指向模型的外部，即进行法矢方向一致化处理，以保证特征提取结果的准确。本文采用MST(minimum spanning tree)进行法矢方向的一致化调整[16]，算法首先为模型中点云定义一个成本函数

cost(p·q)=|d·np+d·nq|

(10)

式中，d为从点p指向点q的单位向量；np、nq分别为点p、q的法矢，p、q是邻接点。

首先从点云模型中选择z值最大的点，作为广度优先遍历的种子点，调整种子点的法矢方向，使得其与向量(0,0,1)的夹角余弦大于0，这样可以保证调整后所有点的法矢指向模型的外侧；接着以成本函数为权值，按广度优先遍历点云数据，由i点遍历到其邻接点j时，如果ni·nj<0，那么将j点的法矢乘以-1；否则nj方向不需要调整。

1.3 显著性指标计算

分析发现，在建筑物点云模型中，墙面等平坦区域点的法矢变化平缓，而起伏较大的区域如墙角等法向量变化剧烈。基于此，本文引入一个显著性指标f(vi)作为特征点判别的依据，f(vi)为中心点K近邻点法矢改变量的均值。即首先计算当前点P的法矢分别与其最近邻的K个点P1,P2,…,PK的法矢之间的夹角，然后计算这K个夹角的平均值作为点P的显著性度量指标。

定义θij为两个点P1和P2的法矢夹角，两个点的法向量分别记为n1(x1,y1,z1)和n2(x2,y2,z2)，则两点法矢夹角计算公式为

(11)

则对于当前点vi，与其K近邻点法矢夹角的平均值的计算方法按式(13)计算，结果即为该点的显著性度量指标值。

(12)

式中，K为以vi为中心点的邻点个数。

2 实例分析

本文试验的硬件环境为英特尔Xeon E3-1241处理器、8 GB内存，软件环境为Windows 7 64位操作系统、VS2013 C++、PCL1.8.0(Point cloud library，点云库)，试验所用数据清华大学校门模型的点云来自徕卡官网的示例数据库，在对数据进行滤波、去噪和对顶部等扫描不到而产生孔洞的地方进行填充等预处理后得到的完整模型点云数量约为90万。

在用移动最小二乘法进行法矢估计时，计算得到的法矢具有二义性会使后续显著性指标的计算出现错误，从而影响特征点的判别，故在计算显著性指标前需先进行法矢方向的调整。如图2所示为移动最小二乘法估计出的初始法矢，从图中可以看出法矢方向比较混乱，有的指向模型外部，有的指向模型内部。按本文方法进行法矢调整后的法矢一致朝向模型的外部，如图3所示。

图2 调整前的法矢

图3 调整后的法矢

分析发现，近邻点个数的选取对计算显著性指标f(vi)有很大影响，邻点个数选取不足或过多都会影响显著性指标计算的准确性，从而影响特征点的判断。如图4所示，本文选取建筑物模型中棱角、圆柱、墙面3个具有代表性位置的点来分析邻点个数的选取对显著性指标的影响。

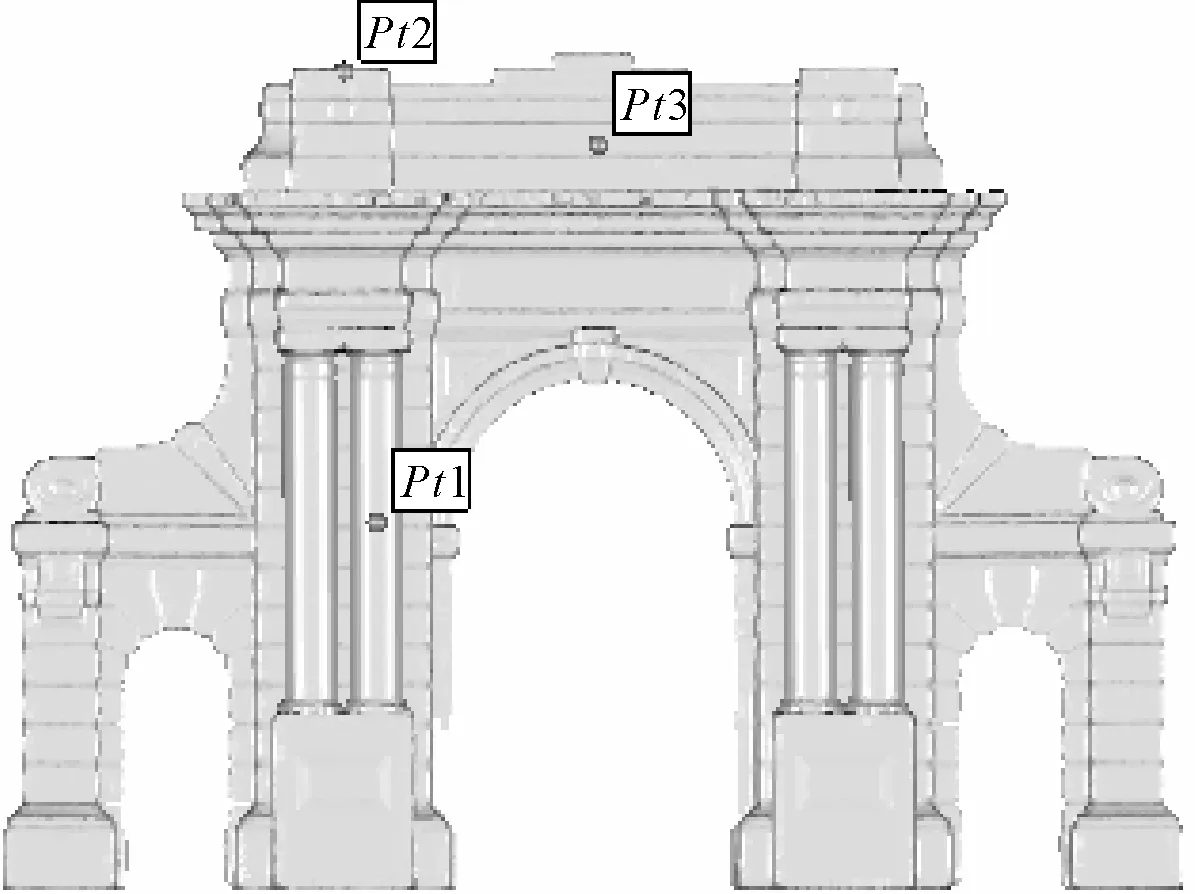
图4 点的位置

如图5所示，随着邻近点数量的增加，墙面上点的显著性指标一直接近于0，但圆柱和棱角上的点随着邻点数的增多显著性指标呈增大的趋势。在邻点数较少时，圆柱和棱角上点的显著性指标随邻点数的增加出现跳跃，此时计算出的显著性指标不稳定，不适合作为判断特征点的依据；在邻点数为11时，二者显著性指标最为接近，此时，其显著性指标分别为0.254 98和0.267 02；在邻点个数大于11后，二者显著性指标增大的趋势就比较稳定，且棱角点的显著性指标一直高于圆柱点。由上述分析可知，邻点个数选为11时显著性指标已趋于稳定，且作为建筑物特征的圆柱点和棱角点显著性指标相差不大，故本文选取11作为本次试验的邻点个数。

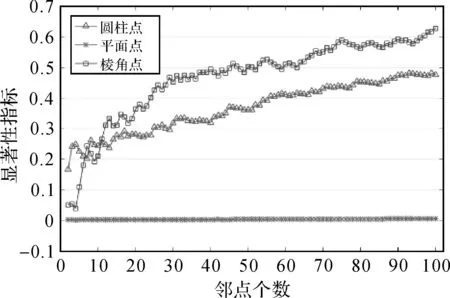
图5 邻点个数对显著性指标的影响

邻点数为11时，计算得到的模型显著性指标如图6所示，从图中可以看出，显著性指标较大的点都分布在建筑物的轮廓及曲率变化较大的位置。

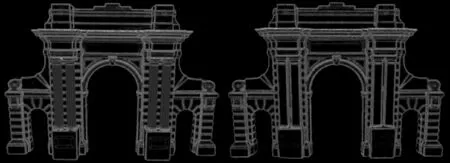
图6 显著性指标分布

用本文算法对原始点云模型进行特征提取，不同阈值下简化点数及简化率见表1。从表中可以看出，提取的特征点数随着简化阈值的变大迅速减少，简化率不断提高，试验结果表明在阈值设为0.30时简化率很高，虽仍能提取出模型的轮廓，但细小的特征已被删除。在阈值为0.25时提取特征点数为96 313，简化率为89.24%，提取的特征比较清晰、完整，如图7(a)、(b)所示，但此时仍有冗余数据存在。

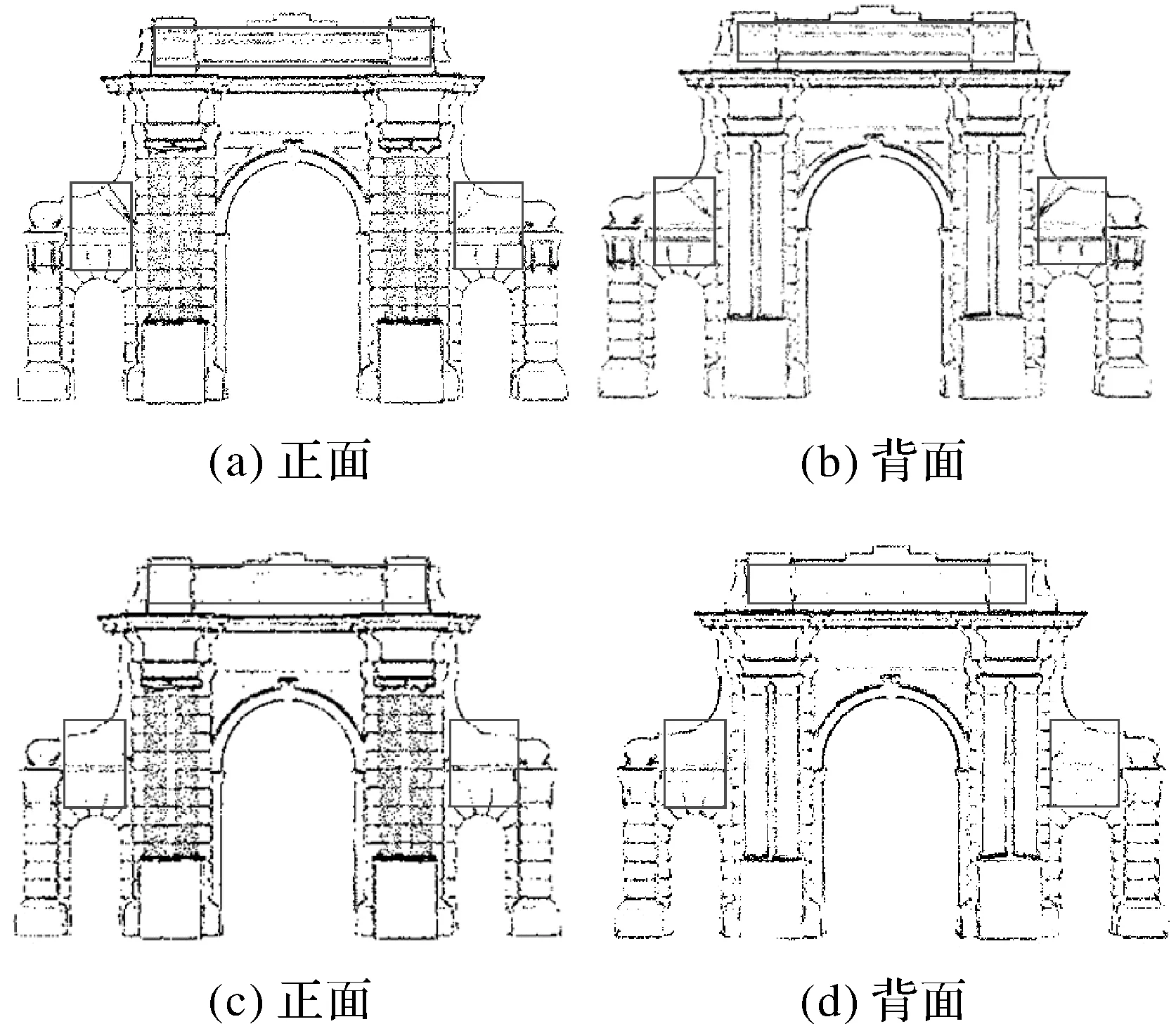
图7 本文算法与传统算法提取的初始特征

考虑提取的特征点比较密集，为进一步减少冗余数据，采用按距离下采样的方法继续对其简化，在距离设为0.088 4时保留特征点数为6219，下采样后简化率为99.31%，如图8(a)、(b)所示，提取出的特征线依然清晰完整。

表1 简化阈值和简化率的关系

为了验证本文算法的优越性，在简化率基本相同的情况下，与采用传统的法向量估计方法进行对比试验，提取特征点数为98 769，简化率为88.96%，试验结果如图7(c)、(d)所示，对其进行下采样后点数为6352，简化率为99.29%，结果如图8(c)、(d)所示。

图8 本文算法与传统算法重采样后的特征

由图7—图8的对比可知，采用传统的法向量估计方法进行特征提取对于小的特征不敏感且提取出来的特征不够完整，而本文算法得到的特征清晰、完整，特别是在对其下采样后冗余数据大大减少的情况下，提取出的特征线更加清晰、简洁、美观。

3 结 语

本文对建筑物点云特征提取和法矢计算的移动最小二乘方法进行了研究，提出了一种基于移动最小二乘法矢估计的建筑物点云特征提取方法。算法采用移动最小二乘法进行法矢估计，然后将邻域法矢夹角的均值作为点的显著性指标进行特征点判别，最后对提取出的特征点集进行下采样。试验中讨论了邻点个数对显著性指标的影响并选出了最佳取值，试验结果表明移动最小二乘估计法矢能显著提高显著性指标的计算精度，从而可以删除绝大多数墙面点，提取出棱角、轮廓和圆柱等上的特征点，对特征点集进行下采样大大减少了冗余数据，从而提取出清晰、简洁、完整的特征线。

参考文献：

[1] 关丽,丁燕杰,张辉,等.面向数字城市建设的三维建模关键技术研究与应用[J].测绘通报,2017(2):90-94.

[2] 冯梅.基于LiDAR和航空影像的三维建模方法探讨[J].测绘通报,2011(12):12-14.

[3] KEDZIERSKI M,FRYSKOWSKA A.Methods of Laser Scanning Point Clouds Integration in Precise 3D Building Modelling[J].Measurement,2015,74:221-232.

[4] 高阳,王留召,李明.车载激光彩色点云的道路标志线提取方法[J].测绘通报,2016(4):28-32.

[5] 李天烁,王晏民,胡春梅.基于激光反射强度的点云自动配准研究[J].测绘通报,2014(S2):143-145.

[6] 王瑞岩,姜光,高全学.结合图像信息的快速点云拼接算法[J].测绘学报,2016,45(1):96-102.

[7] 詹庆明,周新刚,肖映辉,等.从激光点云中提取古建筑线性和圆形特征的比较[J].武汉大学学报(信息科学版),2011,36(6):674-677.

[8] 于海霞,吴侃,敖建锋,等.地面3维激光扫描技术建筑物特征线提取[J].激光技术,2012,36(4):553-556.

[9] 杨林,盛业华,王波.影像辅助下基于地面LiDAR的建筑物特征精细提取方法[J].应用基础与工程科学学报,2015,23(2):299-307.

[10] 陈朋,谭晔汶,李亮.地面三维激光扫描建筑物点云特征线提取[J].激光杂志,2016,37(3):9-11.

[11] 邱彦杰.反向工程中自动精确模型重建的关键技术研究[D].上海:上海交通大学,2011.

[12] 曾清红,卢德唐.基于移动最小二乘法的曲线曲面拟合[J].工程图学学报,2004,25(1):84-89.

[13] 周玉莲.基于法矢信息的点云特征提取技术的研究[D].哈尔滨:哈尔滨工业大学,2012.

[14] DEY T K，SUN J.An Adaptive MLS Surface for Reconstruction with Guarantees[C]∥Proceedings of The Third Eurographics Symposium on Geometry Processing.Vienna：[s.n.],2005:43-52.

[15] WANG H，SCHEIDEGGER C E，SILVA C T.Bandwidth Selection and Reconstruction Quality in Point-based Surface[J].IEEE Transactions on Visualization and Computer Graphics，2009，15(4): 572-582.

[16] 孙金虎,周来水,安鲁陵.点云模型法矢调整优化算法[J].中国图象图形学报,2013,18(7):844-851.