Onanalyticalsolutionofsystemof nonlinear fractional boundaryvalue problemsassociatedwithobstacle

Asif Wheed Syed Tuseef Mohyud-Din Iqr Nz

a Department of Mathematics, COMSATS Institute of Information Technology, Attock, Pakistan

b Center for Research (CFR), University of Islamabad (UoI), Islamabad, Pakistan

1.Introduction

The obstacle problem is a classic motivating example in the mathematical study of variational inequalities. The problem is to fi nd the equilibrium position of an elastic membrane whose boundaries are held fi xed. Fractional obstacle problem is a modi fi ed form of obstacle problem in which fractional derivative is involved. The subject of fractional calculus is a rapidly growing fi eld of research, at the interface between chaos, probability, differential equations, and mathematical physics. In recent years, nonlinear fractional differential equations (NFDEs) have gained much interest due to description of nonlinear phenomena of many real-life problems. The fractional calculus is also considered a novel topic and has gained considerable popularity and importance during the past three decades that has been the subject of specialized conferences and treatises or so, due to mainly its demonstrated applications in numerous seemingly diverse and widespread fi elds of science and engineering.These types of problem are used in diffusion wave equation,signal processing and discovering heat fl ux at the boundary of semi-in fi nite rod, see [26,28,30] and references therein.

In literature, most of the work has been done on the obstacle problems with linear functional till end of the twentieth century, see [1–9] and references therein. In the start of twenty fi rst century, some attention has been paid over obstacle problem with nonlinear functional [18–22,30] but still least attention has been paid to the fractional obstacle problems.

In literature, several techniques have been used by Noor and Trimzi [17] , Al-Said et al. [3] , Khalifa and Noor [8] , Al-Said and Noor [2] , Momani [15] , Gao and Chi [5] and Islam et al. [6] to solve linear system of boundary value problems associated with obstacle problems. Recently, Khan and Akbar[10] and Naher et al. [16] have applied, an ef fi cient analytical technique, (G’/G) expansion method for solving some nonlinear evolution equations associates with such problems. From last few years, attention has been drawn toward nonlinear boundary value problems associated with obstacle problems by Noor et al. [18–22] . Most of these methods are numerical and huge computational work is involved in them. Moreover,numerical methods provide discrete point solution.

Mohyud-Din et al. [13,14,23] have been used variation of parameters method (VPM) for solving a wide class of higher orders initial and boundary value problems. Ma et al.[11] have applied VPM for solving some non-homogenous partial differential equations. Ramos [27] has used this technique to fi nd frequency of some nonlinear oscillators. The multiplier used in VPM is obtained by Wronskian technique and is totally different from Lagrange multiplier of variational iteration method (VIM). Moreover, VPM has removed the higher order derivative term from its iterative scheme which is used in most of the analytical techniques like Adomian decomposition and homotopy perturbation method which is clear advantage of proposed technique over them.

In our work, we use modi fi ed variation of parameters method (MVPM) [18–22] , which is an elegant coupling of variation of parameters method [13,14,23] and Adomian’s decomposition method [24,25,29] . Noor et al. have successfully applied decomposition technique on MHD fl ow problems [24,25] . This modi fi cation was introduced by Noor et al. [18] in 2010. It turned out that MVPM is very fl exible.MVPM has increased the ef fi ciency of both the techniques.The use of multiplier and Adomian’s polynomial together in MVPM increases the rate of convergence by reducing the number of iterations and successive application of integral operators. This technique makes the solution procedure simple while still maintaining the higher level of accuracy. In the present study we implement this technique for solving system of second-order nonlinear fractional boundary value problems associated with obstacle problems.

The most noticeable fact which is necessary to mention here is that all these methods are proposed to solve linear and nonlinear system of boundary value problems associated with obstacle, unilateral and contact problems but less attention is drawn toward nonlinear system of fractional boundary value problems.

2.Preliminaries

In this section, we have given some basic de fi nitions and concepts regarding fractional derivative which we have used in the later section.

There are several de fi nitions of fractional derivatives of orderα＞0 [12,26] . The two most commonly used de fi nitions are the Riemann–Liouville and the Caputo. Each de fi nition uses Riemann–Liouville fractional integration and derivative of whole order.

De fi nition 2.1.The Riemann–Liouville fractional integration of orderαis de fi ned as [12,26]

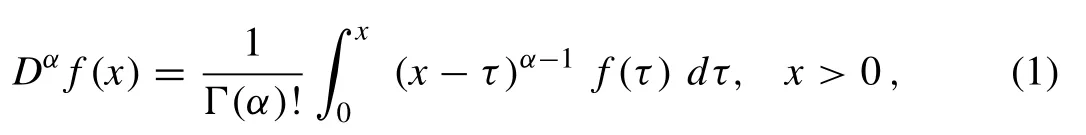
whereαis a parameter, 1 ≤α＜2.

De fi nition 2.2.Caputo fractional derivatives of orderαis defi ned as

Formbe the smallest integer that exceedsα, the Caputo time fractional derivative operator of orderα＞0 is de fi ned as

whereαis a parameter, 1 ≤α＜2 andΓdenotes the gamma function.

In this paper, we consider the following system of fractional boundary value problem:

where 1 ≤α＜2 , with boundary conditionsu(a)=β1,u(b)=β2and continuity conditions ofu(x)andu′(x) at internal pointscanddof the interval [a,b]. Herer,β1andβ2are real and fi nite constants andg(x) is a continuous function on [a,b] .

For simplicity, we will considerf(x,u(x))=f(u). Most of the work is done in the literature with functionf(u) to be linear and continuous in system ( 4 ) while it is noticed that less attention has been given in the case wheref(u)is nonlinear.

Here in this paper, we consider fractional obstacle boundary value problem, wheref(u)in the system ( 4 ) is highly nonlinear with arbitrary choices ofrandg(x). Therefore, we have to use some powerful analytic or numerical technique for obtaining the approximate solution of system ( 4 ).

3.Modi fi ed variation of parameters method (MVPM)

To illustrate the basic concept of the variation of parameter method for differential equations, we consider the general differential equation in operator form.

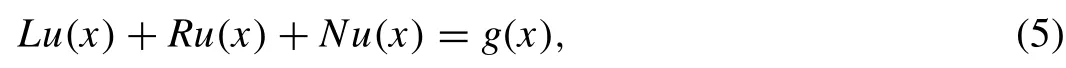
whereLis a higher order linear partial operator with respect to time,Ris a linear partial operator of order less thanL,Nis a nonlinear partial operator andgis a source term.

By using variation of parameters method [13,14,23] , we have following general solution of Eq. (5)

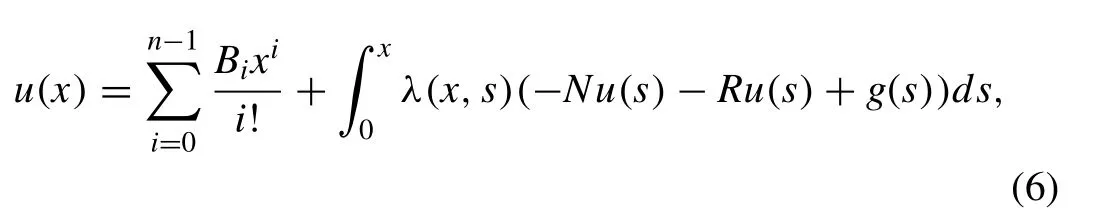
wherenis an order of given differential equation andBi′sare unknowns which are further determined by initial/boundary conditions.λ(x,s) is multiplier, it is obtained with the help of Wronskian technique used in this method. This multiplier removes the successive application of integrals in iterative scheme and it depends upon the order of equation.Noor et al. [13,14,23] have obtained the following for fi nding the multiplierλ(x,s) as

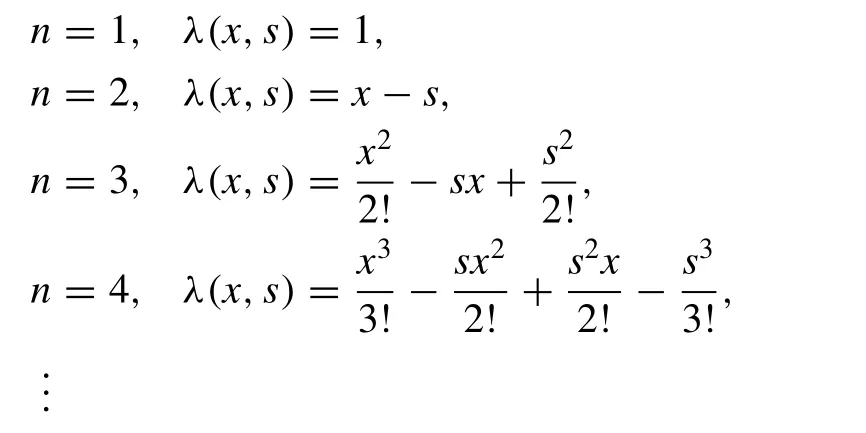
Hence, we have the following iterative scheme from ( 6 )

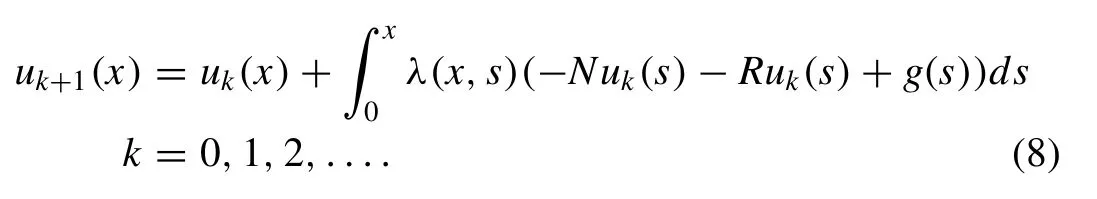
It is observed that the fi x value of initial guess in each iteration provides the better approximation i.e.uk(x)=u0(x),fork= 1,2,···.. However, we can modify the initial guess by dividingu0(x) in two parts and using one of them as initial guess. It is a more convenient way in case of more than two terms inu0(x).

In modi fi ed variation of parameters method (MVPM), we de fi ne the solutionu(x) by the following series

and the nonlinear terms are decomposed by in fi nite number of polynomials as follows

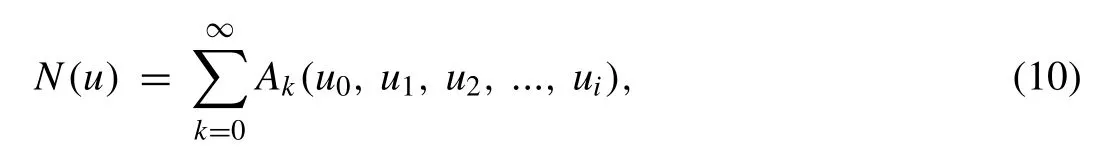
whereuis a function ofxandAkare the so-called Adomian’s polynomials. These polynomials can be generated for various classes of nonlinearities by speci fi c algorithm developed in[24,25,29] as follows

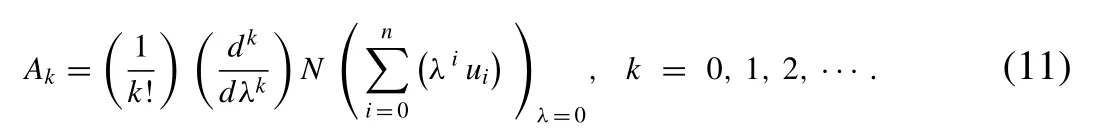
Hence, we have the following iterative scheme for fi nding the approximate solution of ( 5 ) as

依照国军的作派，基层军官是难得一见最高司令长官的，那天顾祝同临战打气获得了空前的反响，不知谁喊了句：人在城在，誓死保卫衢州！

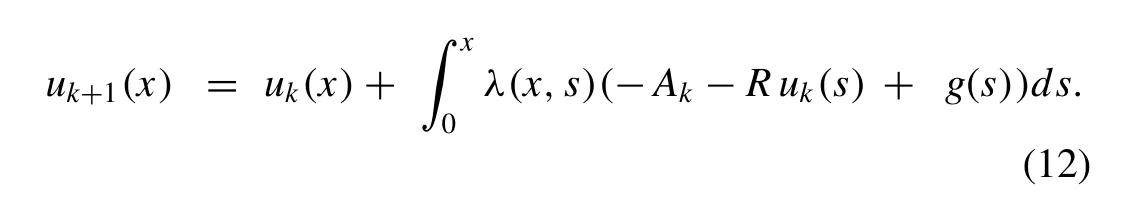
Modi fi ed variation of parameters method (MVPM) for system of second-order nonlinear fractional boundary value problems may be viewed as an important and signi fi cant improvement as compared with other similar method.

4.Applications and numerical results

Example 3.1.Consider following system of nonlinear fractional boundary value problem:

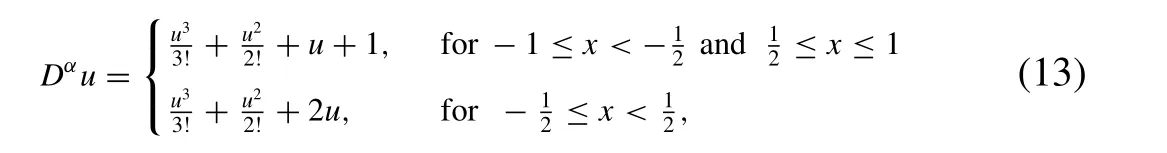
with boundary conditions

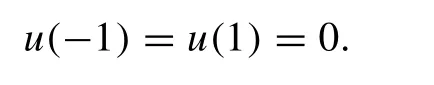
We will use modi fi ed variation of parameters method(MVPM) for solving system of nonlinear fractional boundary value problems ( 13 ). By using MVPM, we have following iterative scheme to solve nonlinear system ( 13 ):

Usingλ(x,s)=x-s, since the governing equation is of 2nd order.

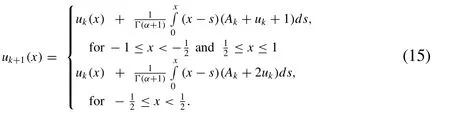
And will calculate the result by takingα= 1,1.2 5 andα= 1.7 5

Forα= 1.

Case 1:for- 1 ≤x＜-

In this case, we implement MVPM as follows

For better approximation, we will decompose initial guess asu0=c1x,and obtain further iterations as follows:

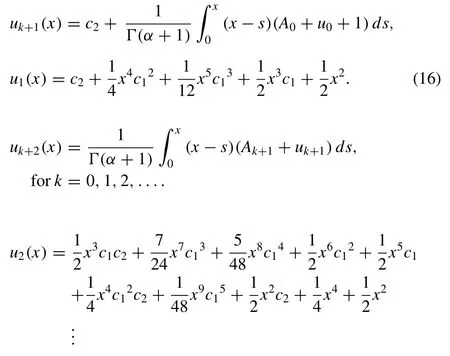
Case 11:

In this case, we have following approximations

Case 111:for≤x≤ 1

In this case, we proceed as follows

By using MVPM, we have the following formula for getting series solution in the whole domain from the above cases

Hence, we have the following series solution after two iterations

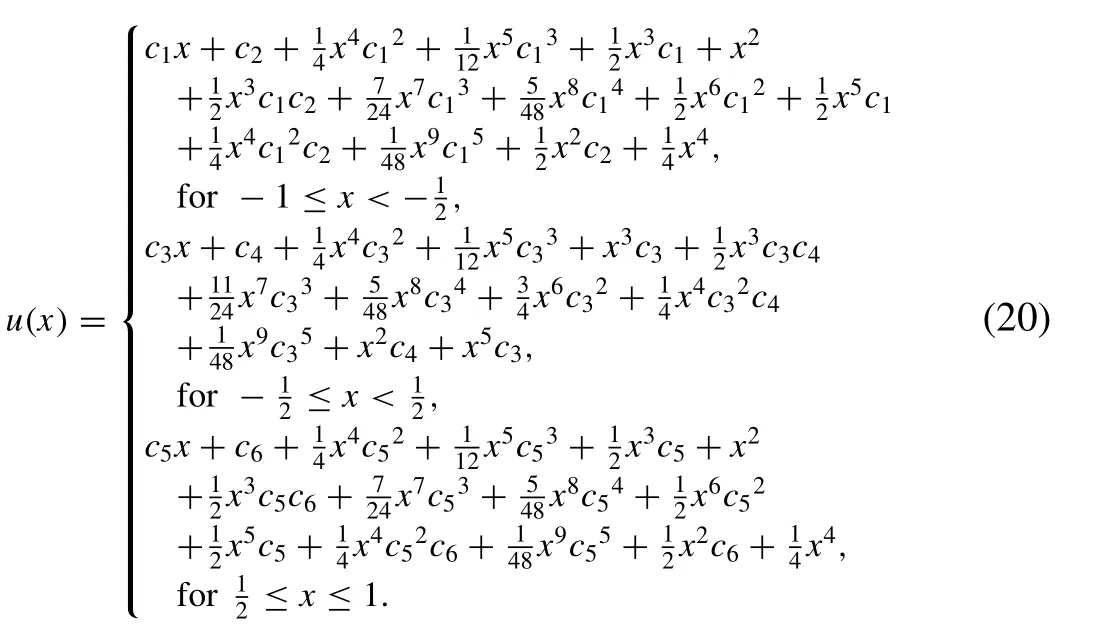
Now we will use boundary conditions and continuity conditions atHence we have the following system of nonlinear equations

By using Newton’s method for system of nonlinear equations (21) , we have following values for unknown constants:

By using values of unknowns from ( 22 ) into ( 21 ), we have following analytic solution of system of second-order nonlinear boundary value problem associated with obstacle problem( 13 ):

In similar manner, we can deduce results forα= 1.25 andα= 1.75.

Forα= 1.25 , we have following analytic solution of system of second-order nonlinear boundary value problem associated with obstacle problem ( 13 )

Under same lines and conditions, we have following analytic solution of system of second-order nonlinear boundary value problem associated with obstacle problem ( 13 ) for

Table 1Analytical solution of system of second-order nonlinear fractional boundary value problem ( 13 ) for different values of αby using modi fi ed variation of parameters method (MVPM).

Further, we can plot the graph for different values ofα, i.e.α= 1,1.25,1.5,1.75.Table 1.

5.Conclusion

In this paper, we have applied modi fi ed variation of parameters method for solving system of nonlinear fractional boundary value problem. The behavior of u(x) for different values of alpha is displayed, individually, in Figs. 1–3 , and collectively in Fig. 4 . From Fig. 4 , which is comparison of all the results for different values of alpha, we have concluded that the obstacle reduces as we increase the fractional value of alpha. It is worth mentioning that we have solved a nonlinear system of fractional boundary value problem by our proposed technique while most of the methods in the literature were proposed to solve linear system of fractional boundary value problems associated with obstacle problems. We took an example of the system which is highly nonlinear in its nature.We analyze that our proposed method is well suited for such physical problems as it provides solution in less number of iterations. It is worth mentioning that the method is capable of reducing the volume of the computational work as compared to the classical methods. The use of multiplier gives this technique a clear edge over the decomposition method by removing successive application of integrals. Therefore, it may be concluded that MVPM is very powerful and ef fi cient in fi nding the analytical solutions for a wide class of system of nonlinear fractional boundary value problems.

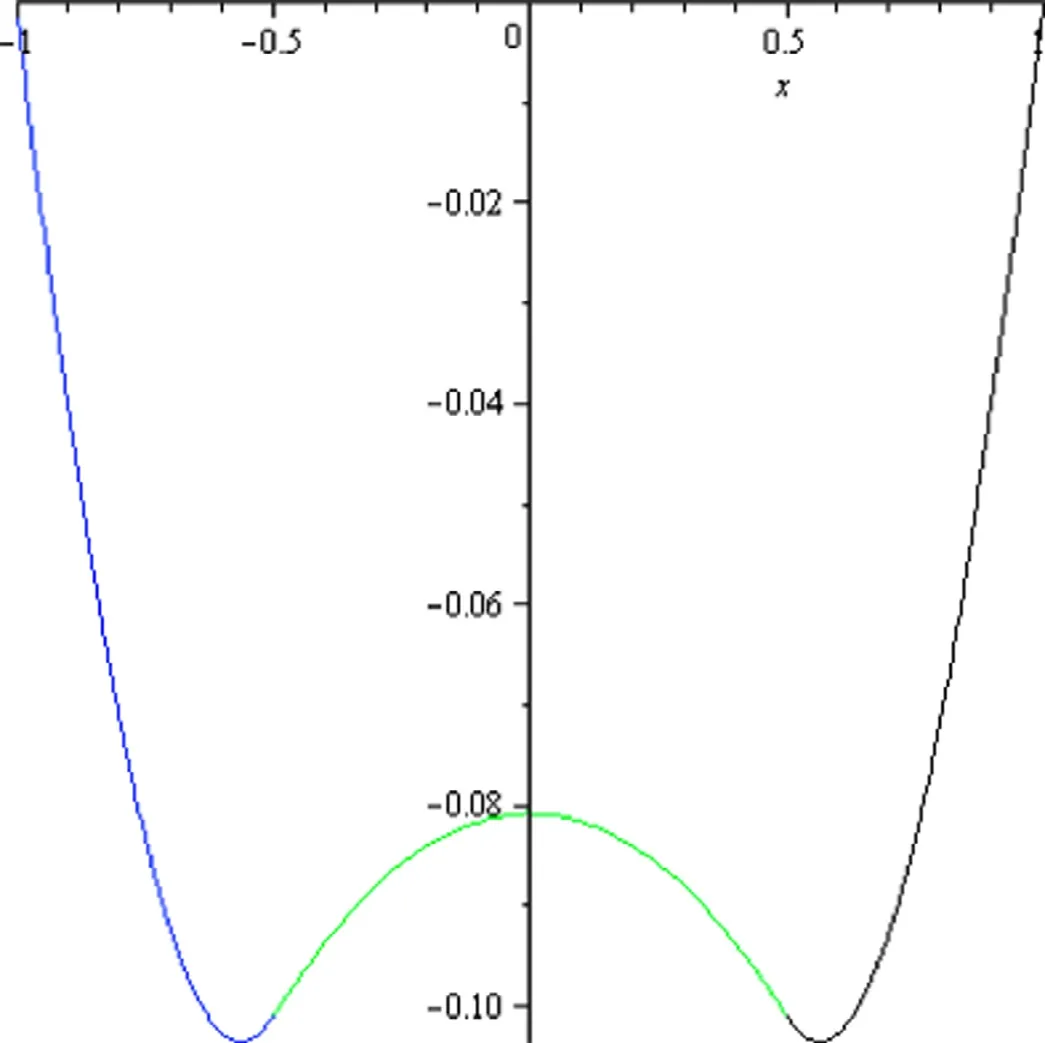
Fig. 1. Graphical representation of analytical solution of system of secondorder nonlinear fractional boundary value problem ( 13 ) for α= 1 by using modi fi ed variation of parameters method (MVPM).

Fig. 2. Graphical representation of analytical solution of system of secondorder nonlinear fractional boundary value problem ( 13 ) for α= 1 . 25 by using modi fi ed variation of parameters method (MVPM).

Fig. 3. Graphical representation of analytical solution of system of secondorder nonlinear fractional boundary value problem ( 13 ) for α= 1 . 75 by using modi fi ed variation of parameters method (MVPM).

Fig. 4. Graphical representation of analytical solution of system of secondorder nonlinear fractional boundary value problem ( 13 ) for different values of αby using modi fi ed variation of parameters method (MVPM).

The Authors are highly grateful to the unknown referee for his/her valuable comments. Moreover, fi rst author Syed Tauseef Mohyud-Din is also thankful to Chairman Bahria Town/Patron and Chairman of FAIRE; Chief Executive FAIRE; Administration of University of Islamabad (a project of Bahria Town) for the establishment of Center for Research(CFR) and the provision of conducive research environment.

[1] E.A. Al-Said , M.A. Noor , D. Kaya , K. Al-Khalid , Int. J. Comput. Math.81 (2004) 741–748 .

[2] E.A. Al-Said , M.A. Noor , Commun. Appl. Nonlinear Anal. 02 (1995)73–83 .

[3] E.A. Al-Said , M.A. Noor , J. Comput. Appl. Math. 143 (2002) 107–116 .

[4] E.A. Al-Said , Int. J. Comput. Math. 78 (2007) 111–121 .

[5] F. Gao , C.M. Chi , Appl. Math. Comput. 180 (2006) 270–274 .

[6] S. Islam , M.A. Khan , I.A. Tirmizi , E.H. Twizell , Appl. Math. Comput.168 (2005) 152–163 .

[7] C. Johnson , Math. Models Methods Appl. Sci. 02 (4) (1992) 483–487 .

[8] A.K. Khalifa , M.A. Noor , Math. Comput. Model. 13 (1990) 51–58 .

[9] A. Khan , S. Bisht , Filomat (formerly Zbornik radova Filozofskog fakulteta, serija Matematika) 26 (5) (2012) 993–1004 .

[10] K. Khan , M.A. Akbar , J. Egyptian Math. Soc. 22 (2) (2014) 220–226 .

[11] W.X. Ma , Y. You , Trans. Am. Math. Soc. 357 (5) (2004) 1753–1778 .

[12] K.S. Miller , B. Ross , An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Inter Science Publication.John Wiley & Sons Inc., New York, 1993 .

[13] S.T. Mohyud-Din , M.A. Noor , A. Waheed , Commun. Korean Math. Soc.24 (4) (2009) 605–615 .

[14] S.T. Mohyud-Din , N. Ahmed , A. Waheed , M.A. Akbar , U. Khan , Thermal Sci. 19 (1) (2015) S69–S75 .

[15] S. Momani , Appl. Math. e-Notes 06 (2006) 141–147 .

[16] H. Naher , F.A. Abdullah , M.A. Akbar , PLoS ONE 8 (5) (2013) 1–7 .

[17] M.A. Noor , S.I. Tirmizi , J. Comput. Appl. Math. 16 (1986) 3870395 .

[18] M.A. Noor , K.I. Noor , A. Waheed , E.A. Al-Said , Int. J. Phys. Sci. 05(16) (2010) 2426–2431 .

[19] M.A. Noor , K.I. Noor , A. Waheed , E.A. Al-Said , Int. J. Phys. Sci. 06(1) (2011) 128–135 .

[20] M.A. Noor , K.I. Noor , A. Waheed , S.K. Khattri , E.A. Al-Said , Int. J.Phys. Sci. 06 (7) (2011) 1798–1802 .

[21] M.A. Noor , K.I. Noor , A. Waheed , E.A. Al-Said , Math. Prob. Eng.(2011) 14 .

[22] M.A. Noor , K.I. Noor , A. Waheed , Math. Comput. Appl. 19 (3) (2014)230–240 .

[23] M.A. Noor , K.I. Noor , A. Waheed , E.A. Al-Said , Int. J. Comp. Math.09 (02) (2012) 16 .

[24] N.F.M. Noor , S.A. Kechil , I. Hashim , Commun. Nonlinear Sci. Numer.Simul. 15 (2) (2010) 144–148 .

[25] N.F.M. Noor , I. Hashim , J. Porous Media 13 (2010) 349–355 .

[26] I. Podlubny , Math. Sci. Eng., 198, Academic Press Inc., San Diego,CA, 1999 .

[27] J.I. Ramos , Appl. Math. Comput. 199 (2008) 39–69 .

[28] J.F. Rodrigues , Obstacle Problems in Mathematical Physics, Elsevier Science Publishers, Amsterdam, 1987 .

[29] A.M. Wazwaz , Comput. Math. Appl. 40 (2000) 679–691 .

[30] W. Zou , W. Wang , Y. Bi ,Math. Methods Appl. Sci. 38 (14) (2015)2911–2921 .