Fuzzyfaulttree analysisofoilandgas leakagein subseaproduction systems
A.S. Cheliyan, S.K. Bhattacharyya
Department of Ocean Engineering, Indian Institute of Technology Madras, India
1.Introduction
into intermediate and basic events that are interrelated by logic gates. The fault tree is analysed using the rules of Boolean algebra with which the tree is represented by an equivalent set of Boolean equations.
In conventional FTA, the failure probabilities of the basic events (BE) are exact values. However, the precise estimation of failure probabilities of theBEs is impractical due to insuffi cient data [19] . Hence, it is often necessary to work with approximate estimates of probabilities in the absence of precise data. In such cases, it is appropriate to use ‘possibility’instead of ‘probability’ [21] . Fuzzy approach provides a way to determine failure probability values when little quantitative information is available ( [21,23] and [31] ) wherein theBEprobabilities are treated as fuzzy numbers. In this scenario, the conventional FTA is replaced by fuzzy fault tree analysis (FFTA).
Lin and Wang [20] combined fuzzy set theories with expert elicitation to evaluate the failure probability of theBEs of a robot drilling system. Shu et al. [29] used fuzzy methods to analyse fault trees for a printed circuit board assembly. Khan and Abbasi [15] developed computer based tool for
Subsea oil production systems consist of wells, fl ow-lines,manifolds, X-trees, risers, pipelines etc. Their operation involves many challenges such as pressure containment, maintenance and fl ow assurance in hostile sea surface and subsea environment. Low temperature and high pressure are the common characteristics of this environment that lead to high costs of maintenance and repair of such systems. Due to the large geographical spread of the subsea oil production systems, the task of risk assessment for gas or oil leakage becomes an extensive task. One of the most powerful risk analysis methods is the fault tree analysis, which is a quantitative method for the computation of failure probabilities of the components of a particular system.
Fault tree analysis (FTA) is a top-down deductive failure analysis for estimating the system reliability using Boolean logic. In FTA, a top event is de fi ned and is further resolved determining the reliability of chemical process industries. Research had been carried out to evaluate the importance of theBEs in fuzzy fault tree analysis (FFTA). Furuta and Shiraishi[6] represented the values of fuzzy membership functions to fi nd the importance of theBEs. Suresh et al. [31] followed Euclidean distance to evaluate the importance and uncertainty of fuzzy basis set. FFTA had been extensively applied to various engineering problems.
The various aspects of safety and reliability of components of subsea systems have received attention, e.g. Hui et al.[11] on reliability estimates of safety instrumented systems and Wanvik [33] on reliability of subsea X-trees etc. However, application of risk based methodologies, speci fi cally the FTA methodology in a subsea system had been rare. The FTA approach, however, had long been extensively adopted in aerospace and nuclear industries. The oil and gas transportation pipelines and wells represent an area where one can fi nd many applications of FTA, FFTA and Bayesian network.Some recent works in this area are by Shan et al. [28] , Guo et al. [8] , Lavasani et al. [17] and Li et al. [18] . These works deal with oil and gas pipelines and abandoned oil and gas wells. Speci fi cally, Lavasani et al. [16] and Shahriar et al.[27] used FFTA in studying offshore oil and gas pipelines.Application to deepwater drilling operation is treated in Rathnayaka et al. [25] and Khakzad et al. [13] . Actual accidents in the oil and gas sector have been studied using a variety of risk assessment methodologies in Khakzad et al. [14] and Kalantarina et al. [12] .
The subsea production systems are complex, operate in harsh environment, and inaccessible, making the repair and maintenance activities costly and time consuming. Therefore,it is imperative that quantitative risk estimation methodologies be adopted in their design and operation. Hu et al. [10] made an attempt to use the FFTA approach to the problem of leakage of oil and gas in a subsea production system, but the details had been sketchy and analysis preliminary. In this paper, this problem has been adopted and an exhaustive FFTA has been carried out. Several importance measures re fl ecting the sensitivity of theTEon theBEs are computed and discussed. The methodology presented in this paper can be readily extended to the subsea systems that include production platforms in an oil and gas fi eld and incorporate the pipeline export system to shore.
It should be noted that FTA, FFTA and several other approaches to quantitative risk analysis (QRA) such as ETA,combined FTA and ETA or bow tie analysis, Bayesian networks etc. have been adopted in many application oriented papers for assessing risk of oil and gas pipelines (both onshore and offshore), submarine pipelines, oil and gas wells(both onshore and offshore), deep water drilling operations,blow out prevention and oil and gas leakage in offshore platforms. In comparison, there had been practically no work(except a preliminary study by [10] ) reported in the literature on application of QRA techniques (speci fi cally FTA and FFTA) in subsea production systems. Whereas in other applications a variety of fault trees have been considered, for subsea production systems, which constitute the mainstay of deepwater production, no generic or detailed fault tree structure is either available or studied. This paper presents, for the fi rst time, a comprehensive analysis of a generic fault tree of a subsea production system. In doing so, a variety of well known and widely used probabilistic risk assessment measures are computed and in addition, a measure called ‘fuzzy weighted index’, which has rarely been used in the literature for systems in the oil and gas sector, is also computed for the chosen subsea production system. The spreads of fuzzy failure probabilities, arising out of uncertainties that are always present in any expert elicitation model that is used in FFTA, both towards left (lower probability) and right (higher probability), affect the top or critical event in an asymmetric manner. This aspect, rarely used and reported in the literature for FFTA studies of oil and gas sector problems, has also been considered in the present work for the subsea production system.
The problem statement, which follows in the next section,considers a generic fault tree model of a subsea system. Typically, FTA of such systems are carried out. However, FFTA approach to this problem, that has not been reported in the literature in a comprehensive way, yields new insight governed by the fuzzy weighted index (FWI) ofBEs that contribute to failure, and such an importance measure can only be used if the fault tree probabilities are fuzzy in nature. Also, the spread of fuzzy probabilities, both to the left and to the right, affects the system failure in a fashion that has not been investigated for a system of this nature in the literature.
2.De fi nition of the problem
The fault tree of the subsea pipeline system with leakage as the top event (TE), built up through deduction, is shown in Fig. 1 .
The leakage could be from
(a) gas or oil well, OR
(b) leakage in pipe, OR
(c) leakage in key facilities such as connector, X-tree, manifold, pipeline end manifold (PLEM) and pipeline end termination (PLET), OR
(d) third party damage.
Leakage in gas or oil well requires
(a) overpressure in well AND
(b) failure of control in well.
Leakage in pipe requires
(a) defect in pipe AND
(b) failure of leakage control in pipe.
Leakage in key facilities could be from
(a) connector leakage, OR

Fig. 1. Fault tree for leakage in subsea production system.
(b) X-tree leakage, OR
(c) manifold leakage, OR
(d) PLEM leakage, OR
(e) PLET leakage.
Defect in pipe could be due to
(a) defect in jumper, OR
(b) defect in fl ow-line, OR
(c) defect in pipeline, OR
(d) defect in riser.
Each one of these could be due to (a) puncture, OR (b) rupture.
Connector leakage requires
(a) defect in connector, AND
(b) failure of connector leakage control.
Similar argument holds for X-tree, manifold, PLEM and PLET leakages.
Defect in connector could be due to
(a) defect in X-tree wellhead connector, OR
(b) defect in pipe connector, OR
(c) defect in pipe manifold connector, OR
(d) defect in pipe PLEM connector, OR
(e) defect in pipe PLET connector.
From the above description, it is seen that the problem is a generic one and the deductive structure using OR and AND logic gates lends itself to adaptation for any practical leakage problem of a subsea oil and gas production system.The task is to quantify the failure probability of the leakage in the subsea pipeline system, which is the top event. TheBEs that lead to the failure of theTEdo not have well quanti fi ed probabilities. This, therefore, requires a fuzzy treatment of the FTA. Furthermore, the events that have major contribution to the failure of theTEare of interest.
The fault tree in Fig. 1 has 26 basic events (BEs) numberedX1,X2, …,X26; 14 intermediate events numberedX27,X28,…,X40; all leading to the top event (TE) which is numberedX41. TheBEs are numbered fi rst, the intermediate events next and theTElast. The intermediate events are numbered in such a way that the event number of an intermediate event is connected (downward) to events with smaller event numbers.
3.FTA basics
The fault tree presented in Fig. 1 is a combination of‘AND’ and ‘OR’ gates. The ‘AND’ gate implies that the output event will occur if all the input events occur, while the‘OR’ gate implies that the output event will occur if any one of the input events occur. Let a top event (TE), designated byT, be connected to the basic events (BEs)X1toXN, whereNis the number ofBEs. The probability of failure of the eventXiisP(Xi). Then, the probability of failure of theTE, denotedP(T), for the cases when the connecting gate is either AND or OR is given by:
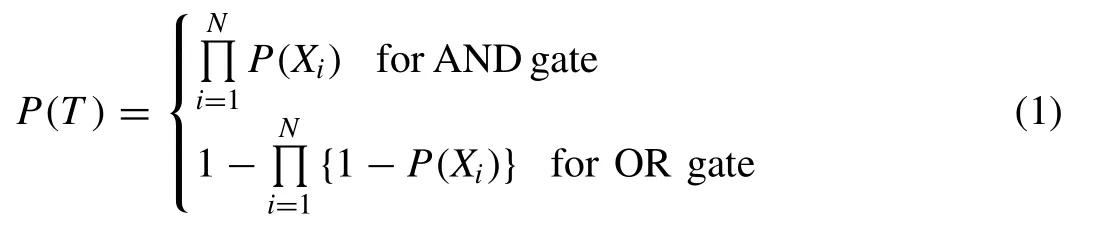
The failure probability of theTEin a fault tree (as in Fig. 1 ) is assessed by obtaining its minimal cut sets (MCS)which are minimal, necessary and suf fi cient conditions for the occurrence of theTE. Once all theMCSs, denotedCi(i= 1,2, …,Nc) whereNcis the number ofMCS, are determined,the failure probability of theTE, denotedP(T), is given by

whereP(Ci) is the probability of failure ofCi. As long as the failure probabilities of theBEs are small, (i.e.P(Xi)<<1),the above estimate ofP(T) can be approximated well by

A typicalMCSis a collection of theBEs and may be denoted as

whereNjis the number ofBEs inCj, also called the order of theMCS.
The determination ofMCSs from the fault tree follows a well-established procedure, a detailed account of which may be found in Vesely et al. [32] . The cut sets are the unique combinations of component (i.e.BE) failures that can cause system (i.e.TE) failure. A cut set is minimal when anyBEis removed from the set, the remainingBEs collectively are no longer a cut set. A longerMCS(i.e. consisting of more number ofBEs, also called the order of the cut set) makes theTEless vulnerable to thatMCS. In other words, a cut set of order one is more critical than a cut set of order two or higher. When a cut set has only oneBE, theTEwill occur as soon as thisBEoccurs. When a cut set has twoBEs, both of these have to occur at the time to cause theTEto occur.Also, higherNcimplies higher vulnerability.
4.System data and analysis procedure
4.1. Failure probabilities of the basic events
In subsea oil production systems, there is a lack of observed data and yet, to carry out FTA, the occurrence probabilities of theBEs must be known. Expert elicitation or expert opinion provides information to compute the failure probability of theBEs which includes interview, Delphi method,ranking and scaling, method of paired comparison [9] etc.Indirect interaction/interview is adopted in the present study.A de fi nite advisory table is made and given to the experts.The experts give the opinions based on their experience. Experts apply natural linguistic expressions such as ‘very low’,‘low’, ‘medium’, ‘high’ and ‘very high’ to describe the probability of theBEs. Fuzzy set theory is used to handle these linguistic expressions using fuzzy set theory.
Expert judgement models play a crucial role in quantitative risk assessment. Several models are available in the literature [26] such as classical expert model and Bayesian expert model. Expert judgements can suffer from bias, dispersion and independency [2,4] . There are statistical tests that can restrict the judgement data from multiple experts from these de fi ciencies. Checks on variance and correlation may also be necessary. The choice of a model, however, must satisfy the need of the risk analyst and this is achieved, and in practice dictated, by the protocol followed by a particular industry. The expert judgement evaluation protocol followed by industry is achieved by ‘past experience’ and hence is usually reliable. In the present work, such a protocol has been used for analysis.
4.2. Expert elicitation
Experts from different fi elds are selected to give their assessment of the failure probabilities of theBEs in the form oflinguistic expressions based on their experience and knowledge about leakage in subsea pipeline systems. This has been carried out by designing an appropriate questionnaire. The experts’ opinions are evaluated based on their respective weighting factors since experts differ in opinion and their levels of expertise. The weights are assigned for attributes such as (a)title or designation, (b) length of experience, (c) education level and (d) age in a scale of 1 to 5 as shown in Table 1 .The weighting score of an expert is the summation of these weights for attributes. The weighting factor for each expert is then computed by

Table 1Weights for attributes.

Table 2Experts and their weighting factors.
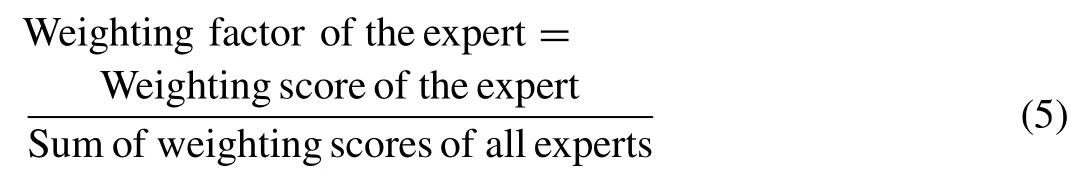
Table 2 gives the weighting scores and weighting factors computed for each of the ten experts consulted in this study.The data in Tables 1 and 2 closely follow the industry protocol of an offshore oil and gas industry.
4.3. Linguistic expressions to fuzzy numbers
A numerical approximation system was proposed by Chen and Hwang [1] to convert linguistic expressions to fuzzy numbers. The linguistic expressions ‘very high’, ‘high’, ‘medium’,‘low’ and ‘very low’ are represented as VH, H, M, L and VL, respectively. These are related to the fuzzy membership functions as shown in Fig. 2 which consist of both triangular and trapezoidal fuzzy numbers. The triangular fuzzy numbers are converted into trapezoidal fuzzy numbers for the ease of computation. Each trapezoidal fuzzy number is represented by four values (a,b,c,d) for the fi ve membership functions(VH, H, M, L and VL) of Fig. 2. The opinions of ten experts for allBEs are summarised in Table 3 .
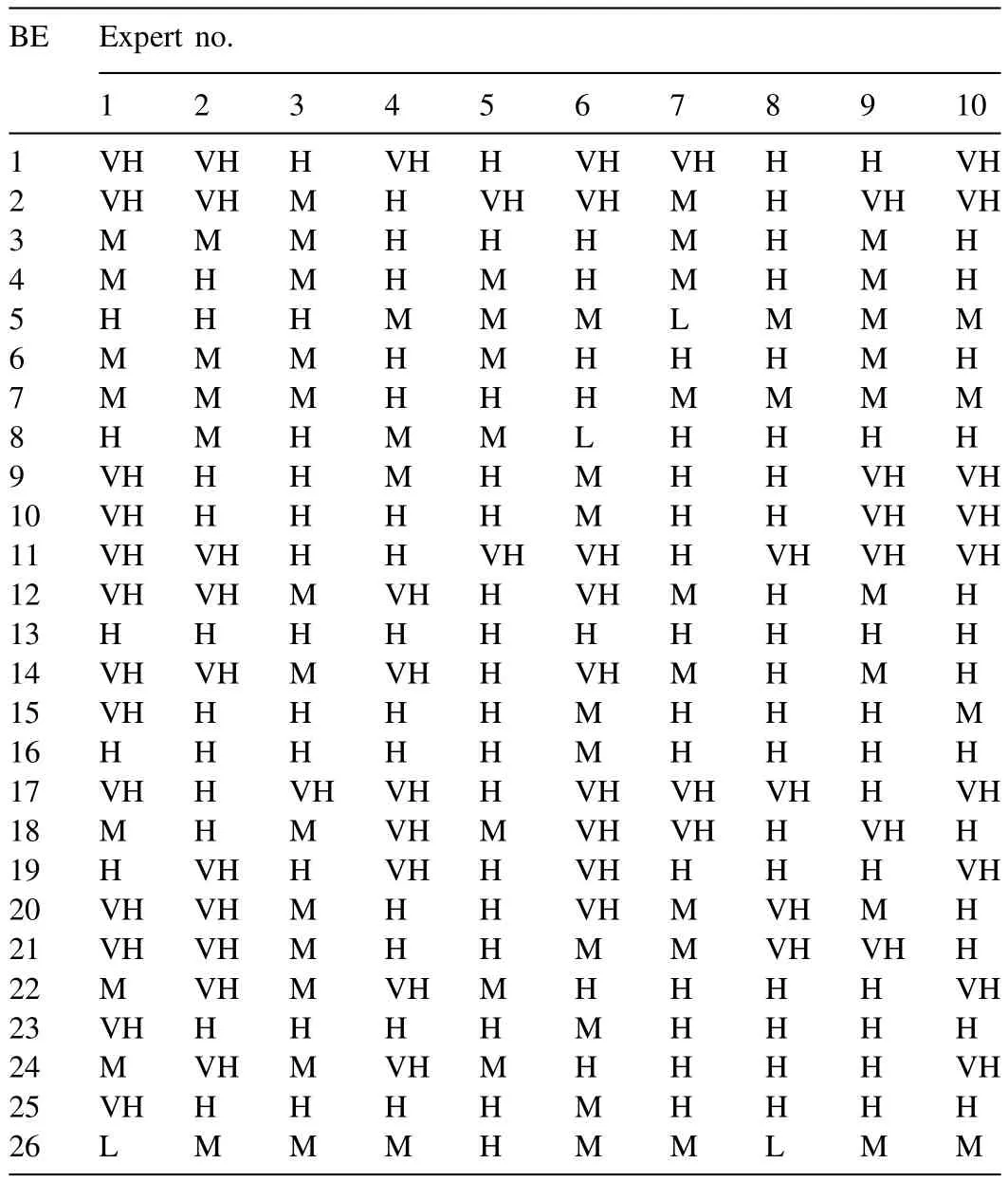
Table 3Expert opinions on failure of the basic events.

Fig. 2. Fuzzy membership function for fuzzy numbers.
4.4. Aggregation for deriving the estimates of the basic events
EveryBEis given a rating by the experts as shown in Table 3 . All the ratings for a singleBEmust be combined or aggregated to obtain a single opinion. One of the methods to obtain the aggregate is the linear opinion pool [3] given by
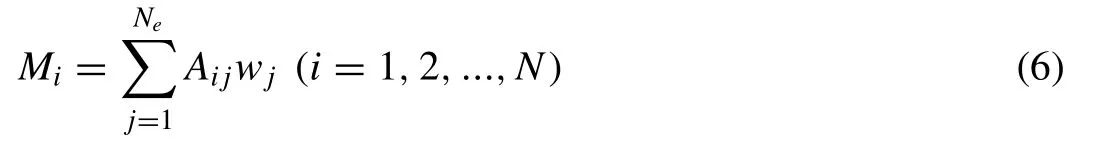
whereNis the number ofBEs ( = 26 in Fig. 1 ),Neis the number of experts ( = 10, see Table 4 ),wjis the weighting factor of the expertj(given in the last column of Table 2 ),Aijis the linguistic expression (eithera, orborcord) of theithBEgiven by the expertjas given by Table 3 andMiis aggregated (resultant) trapezoidal fuzzy number of theBEXi. The values ofMiare shown in the second column of Table 4 for allBEs.
4.5. Defuzzi fi cation process
The defuzzi fi cation process converts a fuzzy number to a single point value called fuzzy possibility score (FPS) which represents the possibility of theBE. The defuzzi fi cation process that has been used here is the left and right fuzzy ranking method proposed by Chen and Hwang [1] . The left and right utility score of a fuzzy number can be obtained with the help of Fig. 3 and the corresponding expressions are:


Table 4Data of the basic events.
TheFPScan be obtained by:


Fig. 3. Representation of fuzzy number and its left and right utility score.
The defuzzi fi cation of allBEs leads to theirFPSvalues and these are given in the third column of Table 4 .
4.6. Converting fuzzy possibility score to fuzzy failure probability
TheFPSof allBEs (Xi) needs to be converted to their fuzzy failure probability,P(Xi). The fuzzy failure probability,as de fi ned by Onisawa [24] , is given by:

The failure probabilities of allBEs are given in the fourth column of Table 4 .
5.Failure probability of the top event
The failure probability of the top event is given by Eq. (2) and it can also be approximated by Eq. (3) . TheMCSs of theTEare determined and these are listed in Table 5 . There are 19 minimal cut sets for theTE(Nc= 19). These sets contain no more than twoBEs and thus the order of theMCSs is 2 ( = ¯Nc). The failure probability of theTE(i.e. for the leakage of oil and gas in the system) can be computed either using Eq. (2) , which is exact; or using Eq. (3) , which is an approximation. The difference between the exact and approximate estimates are of higher order and usually insigni fi cant in practice.

Table 5Importance measures of basic events and their rankings.
The failure probabilities of the intermediate events are also calculated by fi rst determining theMCSs corresponding to each intermediate event (by considering the intermediate event as theTE) and then using Eq. (3) .
6.Importance measures
6.1. Rationale
There are various importance measures proposed in the literature that provide information on the contribution of theBEs to the occurrence of theTE. These measures help identify the weakest link in the system and also help evaluation of alternative design approaches. The measures discussed here are (a) cut sets importance, denoted CSI, (b) probabilistic importance, denotedPI, (c) critical importance, denotedCIand (d) fuzzy weighted index, denotedFWI.
6.2. Probabilistic importance
The probabilistic importance (also called the Birnbaum’s measure) is de fi ned as the rate of change in total probability of the system with respect to changes in probabilities of theBEs [22] . It is the measure of the functional margin of the system design for theBE. The probabilistic importance (PI)is given by

The values ofPIof allBEs with their ranking are given in Table 5 .
6.3. Critical importance
The critical importance (CI) is given by

If it is given that the system has failed, the critical importance of aBEXiis a measure that the failure is caused by this event [34] . In its de fi nition, the probabilistic importance measure is adjusted to the failure probability of theBEas a fraction of the total failure probability of the whole system.Therefore, if the probabilistic importance of aBEis high, but the failure probability of theBEis low with respect to the total failure probability of the system, then the critical importance will automatically adjust its estimate to a lower value[22] . The values ofCIof allBEs with their ranking are given in Table 5 .
6.4. Cut sets importance
The relative contribution of the individualMCSs to theTEis given by a measure called the cut set importance (CSI),proposed by Fussel–Vesely [22] . It is given by

For higher rankedCSI(highest rank being 1), it is imperative not to allow the long term average probabilities to increase further. This measure can also be interpreted as the amount of allowed degradation as a function of risk increase.The values and the ranking of CSI of allMCSs are given in Table 6 .
7.Fuzzy weighted index of basic events
A fuzzy weighted index (FWI) is another importance measure where the contribution of each basic event to the failure of the top event is measured in terms of impact or weight[5] . This is estimated by eliminating each basic event from the fault tree and evaluating the total probability of the system. The difference between the total probability of theTEwith all the basic events and the total probability of theTEby eliminating one basic event would be the fuzzy weighted index. This approach can only be followed when the basic events are fuzzy in nature.
TheFWIis calculated by fi rst converting the deduced crisp probabilities of theBEs to fuzzy probabilities. This is done based on the guidelines given in Table 7 , and a triangular fuzzy number is obtained with the lower and upper bounds.The fuzzy probability of theTEis calculated by following the usual procedure through the minimal cut sets of the fault tree. TheFWIof a particularBEis computed by calculating thedistancebetween ‘the fuzzy probability of theTEwith all basic events (A1)’ and ‘the fuzzy probability of theTEby eliminating the particular basic event (A2)’. The difference assists in understanding the contribution of the particular basic event to the failure of the top event.
TheFWIis thedistancebetween the two triangular fuzzy numbersA1andA2. It is given by [7]

whereA1=(a1,b1,c1)andA2=(a2,b2,c2)are the triangular fuzzy numbers andδis the distance betweenA1andA2. The values ofFWIof allBEs with their ranking are given in Table 5 .
8.Spreads of the fuzzy failure probability
The fuzzy failure probability for each basic event is a crisp value, which has been computed from expert opinions. These computed values would have inevitable uncertainties involved in them, as they are purely based on the opinion, judgement and experience of the experts. The extent of uncertainty in the computed values is indicated by the ‘spread’ of the fuzzy failure probabilities. The width of the membership function is the spread of the crisp value [30] . This function consists of a monotonically increasing functionL(x) and a monotonically decreasing functionR(x) which intersect each other at the maximum (crisp) value. It has the form (see Fig. 4 )

In the above,mis the crisp value of the fuzzy number andαandβare the measures of the left and right spreads,respectively. Thus, a fuzzy number is given by the triple (m,α,β). The two algebraic operations on fuzzy numbers thatare required for a fault tree consisting of OR and AND gates are the addition and multiplication of two fuzzy numbers with spreads given by, say, by (m1,α1,β1) and (m2,α2,β2). These operations are given by

Table 6Minimum cut sets for the top event, their importance measures and ranking.

Table 7Lower and upper bounds to convert crisp probability to fuzzy probability.

Fig. 4. Left and right spreads of the fuzzy failure probability.

In Eq. (1) , the probabilitiesP(Xi) are the crisp valuesmi(i= 1 to N), each associated with a left spread measureαiand a right spread measureβi. The expansion ofP(T) requires addition and multiplication ofP(Xi) in various combinations and these are accomplished by the rules of Eq. (15) .
Denotingα=CLmandβ=CRmso thatm-α=m(1 -CL) andm-β=m(1 -CR) and as a result 100CLand 100CRare percentage measures of left and right spreads. The fuzzy failure probability of allBEs has been fuzzi fi ed by taking a left and right spread of 5% (i.e.CL=CR= 0.05) and 10% (i.e.CL=CR= 0.1). Considering these spreads, the top event probability has been calculated.The values obtained for all non-basic events, including thetop event, are listed in Table 8 with their spread measures in percentage. In Table 8 , the MCSs for the 14 intermediate events (X27 to X40) of the fault tree of Fig. 1 and their failure probabilities are also shown. The left and right spreads of theTEprobability as functions of the equal left and right spreads of the probabilities of all theBEs are plotted in Fig. 5 .

Table 8Left and right spread (in percentages) of non-basic events including the top event.
At this stage, it may be of interest to evaluate this dependence of the left and right spreads of theTEprobability on the spreads of the probabilities of all theBEs in the case of conventional FTA as against fuzzy FTA. These plots for the conventional FTA are shown in Fig. 6 , which can be compared with those of Fig. 5 for fuzzy FTA.
9.Discussion of results
The fuzzy set theory has been used in the fault tree analysis of a subsea production system to quantify the ‘probability oftheleakage’, which is the top event (X41) and this probability is computed as 0.017825 using Eq. (2) and 0.01777(see Table 8 ) using Eq. (3) , showing negligible effect of the higher order terms.

Fig. 5. Spreads of the TE as functions of equal spreads of the BE s in FFTA (solid line: right spread; dashed line: left spread).

Fig. 6. Spreads of the TE as functions of equal spreads of the BE s in conventional FTA (solid line: left spread; dashed line: right spread).
The fault tree has only one fi rst orderMCSconsisting of‘thirdpartydamage’ (X26) and the restMCSs are of second order. As a result,X26has the highest rank (i.e. rank 1) ofPI(see Table 5 ) and the correspondingMCS(i.e. C19) also has the highest rank (see Table 6 ). Next in the order of importance of theBEs, the events ‘failureofleakagecontrolin pipe’ (X11) and ‘failureofconnectorleakagecontrol’ (X17)affect the overall system failure signi fi cantly since they havePIranks of 2 and 3 respectively andCI(andFWI) ranks of 1 and 2 respectively (see Table 5 ). Next in the order of importance of theMCSs,C9andC1haveCSIranks of 2 and 3 respectively (see Table 6 ). TheMCSC9consists of ‘rupture inriser’ (X10) and ‘failureofleakagecontrolinpipe’ (X11),whereasMCSC1consists of ‘overpressureinwell’ (X1) and‘failureofcontrolinwell’ (X2) and therefore these events (X1,X2andX10) are next in order of importance afterX11andX17.
From Table 8 and Fig. 5 , it is seen that the left and right spreads of theTE(i.e.X41) are less than 25% of that of theBEs (e.g. 2.38% left spread ofTEvs.10% left spread of allBEs). This is encouraging for the overall system because it means that the uncertainty of the fuzzy crisp value of theTEwill be signi fi cantly less that the uncertainty ofBEs. In other words, the crisp value of theTEprobability is robust.The opposite is true for conventional FTA as can be seen from Fig. 6 . The uncertainty of the evaluatedTEprobability is almost 100% more than the uncertainty ofBEs. In other words, the left and right spreads, which represent the uncertainty band of the probability of theBEs, leads to a much larger (about 100% more) uncertainty band of the probability of theTEin conventional FTA, whereas it leads to a much smaller (about 75% less) uncertainty band of the probability of theTEin fuzzy FTA. This underscores the inherent desirability of a fuzzy description of theBEprobabilities, and hence the fuzzy route to FTA.
Leakage of oil or gas in any offshore, onshore or subsea production systems may result in serious accidents such as fi re and explosion which may involve serious economic as well as personnel losses. This paper deals with FTA of a subsea system. The FTA only evaluates the probability of occurrence of the leakage event. This must be followed up with event tree analysis (ETA) which establishes the variety of consequences that may follow this leakage event established by FTA. A combined FTA-ETA is called ‘bow-tie’ analysis (e.g. [28] ).At the end of ETA, one obtains the risk measures of various consequences and hence the risk pro fi le of the entire system.This risk pro fi le can be used to draw up managerial decisions regarding inspection and monitoring strategies of various system components. The fuzzy ETA does not seem to have been used for any subsea production system and work in that direction is needed to draw up integrity management of such systems based on the fuzzy approach to risk analysis.
10.Conclusion
A probabilistic failure analysis of the leakage of the gas and oil in a subsea oil and gas production system has been carried out using fuzzy fault tree analysis that requires expert elicitation of the failure probabilities of the basic events in a fuzzy framework. A number of importance measures have been evaluated and discussed which helps to identify the weakest links that may cause leakage in the system. Especially, the fuzzy weighted index measure, that is relatively less used in the literature, has been obtained in this work. The analysis is extended to evaluate the uncertainty involved in the failure probability of the top as well as intermediate events due to the assumed uncertainty levels of the basic events using a left and a right spread of errors. It has been found that a large error band of the basic events yields a much smaller error band of the top event failure probability making it robust to the variations of the basic events. It is shown that the opposite is true for conventional fault tree analysis and hence a fuzzy route to the fault tree analysis is more desirable.
The application of FTA to large subsea production systems that include production platforms as well as export pipelines to onshore infrastructure in a complex oil and gas fi eld can be attempted by extending the methodology presented in the present work.
[1] S.J. Chen , C.N. Hwang , Fuzzy Multiple Attribute Decision Making Methods and Applications, Springer, Berlin, 1991 .
[2] S. Chhibber , G. Apostolakis , D. Okrent , Reliab. Eng. Syst. Saf. 38 (1–2)(1992) 27–45 .
[3] R.T. Clemen , R.L. Winkler , Risk Anal. 19 (2) (1999) 187–203 .
[4] R. Cook , Experts in Uncertainty, Oxford University Press, New York,1991 .
[5] R. Ferdous , F. Khan , B. Veitch , P. Amyotte ,Process Saf. Environ. Prot.J. 87 (4) (2009) 217–226 .
[6] H. Furuta , N. Shiraishi , Fuzzy Sets Syst. 12 (3) (1984) 205–213 .
[7] G. Gojadziev , M. Bojadzeiv , Fuzzy Sets, Fuzzy Logic, Application,World Scienti fi c Publishing, 1995 .
[8] Y. Guo , X. Meng , D. Wang , T Meng , S. Liu , R. He , J. Nat. Gas Sci.Eng. 33 (2016) 18–29 .
[9] D.M. Hunns , in: A.E. Green (Ed.), High Risk Safety Technology, John Wiley & Sons, 1982, pp. 204–208 .
[10] X. Hu , H. Zhang , M. Duan , M. Ni , Int. J. Energy Eng. 2 (3) (2012)79–85 .
[11] J. Hui , M. Lundteigen , M. Rausand , J. Risk Reliab. 226 (6) (2012)646–655 .
[12] M. Kalantarnia , F. Khan , K. Hawbolt , Process Saf. Environ. Prot. 88(2010) 191–199 .
[13] N. Khakzad , F. Khan , P. Amyotte , Saf. Sci. 57 (2013) 108–117 .
[14] N. Khakzad , S. Khakzad , F. Khan , Nat. Hazards 74 (2014) 1759–1771 .
[15] F.I. Khan , S.A. Abbasi , J. Hazard. Mater. 75 (1) (2000) 1–27 .
[16] M.R.M. Lavasani , J. Wang , Z. Yang , J. Finlay , Int. J. Marine Sci. Eng.1 (1) (2011) 29–42 .
[17] S.M. Lavasani , N. Ramzali , F. Sabzalipour , E. Akyuz , Ocean Eng. 108(2015) 729–737 .
[18] X. Li , G. Chen , H. Zhu , Process Saf. Environ. Prot. 103 (2016) 163–173 .
[19] G.S. Liang , M.J. Wang , Microelectron. Reliab. 33 (2) (1993) 583–597 .
[20] T.C. Lin , M.J. Wang , Reliab. Eng. Syst. Saf. 58 (6) (1997) 205–231 .
[21] K.B. Misra , G.G. Weber , Fuzzy Sets Syst 37 (2) (1990) 139–160 .
[22] M. Modarres , Risk Analysis in Engineering: Probabilistic Techniques,CRC publishing, USA, 2006 .
[23] T. Onisawa , Fuzzy Sets Syst. 37 (3) (1990) 267–287 .
[24] T. Onisawa , Fuzzy Sets Syst 27 (2) (1998) 87–103 .
[25] S. Rathnayaka , F. Khan , P. Amayotte , J. Risk Reliab. 227 (1) (2013)86–105 .
[26] T. Rosqvist , On the Use of Expert Judgment in the Quali fi cation of Risk Assessment, Helsinki University of Technology, Espoo, Finland, 2003 Ph.D thesis .
[27] A. Shahriar, R. Sadiq, S. Tesfamariam, J. Loss Prev. Process Ind. 25(3) (2012) 505–523 .
[28] X. Shan , K. Liu , P.L. Sun , Sci. Program. (2017) 1–11 3639524 .
[29] M.H Shu , C.H. Cheng , J.R. Chang , Microelectron. Reliab. 46 (12)(2006) 2139–2148 .
[30] D. Singer , Comput. Chem. Eng. 14 (3) (1990) 259–266 .
[31] P.V Suresh , A.K. Babar , V.V. Raj , Fuzzy Sets Syst. 83 (1996) 135–141 .
[32] W.E. Vesely , F.F. Goldberg , N.H. Roberts , D.F. Haasl ,Fault Tree Handbook, US Nuclear Regulatory Commission, Washington D.C., USA,1981 .
[33] P.G. Wanvik , Reliability Assessment of Subsea X-mas Tree Con fi gurations, NTNU, Norway, 2015 MS thesis .
[34] G. Yang , Life Cycle Reliability Engineering, Wiley, USA, 2007 .
 Journal of Ocean Engineering and Science2018年1期
Journal of Ocean Engineering and Science2018年1期
- Journal of Ocean Engineering and Science的其它文章
- Travelingwave solutionstosome nonlinear fractional partialdifferential equationsthroughtherational(G ′ /G ) -expansionmethod
- Anumerical techniquebasedon collocation methodfor solvingmodi fi ed Kawaharaequation
- RiskassessmentofLNGandFLNGvessels during manoeuvringinopen sea
- Onanalyticalsolutionofsystemof nonlinear fractional boundaryvalue problemsassociatedwithobstacle
- Coupled boundary element methodand fi nite element methodfor hydroelasticanalysisoffl oatingplate
- Multiple soliton solutionsforthe(3+1)conformable space–time fractional modi fi edKorteweg–de-Vriesequations
