RiskassessmentofLNGandFLNGvessels during manoeuvringinopen sea

Ngi Adussmie Mohmed Doos Ismil Elferjni Chi Shuhong Aduslm Alktiwi

a National Centre for Maritime Engineering and Hydrodynamics, Australian Maritime College, University of Tasmania, Launceston, Australia

b Marine and Offshore Engineering, Faculty of Engineering, University of Tripoli, PO Box 13275, Tripoli, Libya

c RMIT University, Melbourne VIC 3001, Australia

Abbreviationsandnotations

A 3rd party assets

a,b,cElements of a fuzzy set

CConsequence

CI Consequence Index

CML Cargo/Monetary Loss

E Environment

ES Effect on Ship

FLNG Floating Lique fi ed Natural Gas

GMF Gaussian Membership Function

HijHazard inith phase

HS Human Safety

LNG Lique fi ed Natural Gas

MMean value of Gaussian function

MF Membership Function

PProbability

p,q,rConsequent parameters

PI Probability Index

QRM Qualitative Risk Matrix

RRisk

RI Risk Index

SOperational phase

TMF Triangular Membership Function

wWeight factor

σStandard deviation of Gaussian function

1.Introduction

Over the last decades, subsea pipelines have been used for exporting natural gas partially processed from offshore platforms to LNG plants located onshore. This approach, however, is only feasible for offshore gas fi elds located within a reasonable distance from an existing offshore pipeline network or from the onshore LNG plants [1] . Currently, the development of Floating Lique fi ed Natural Gas (FLNG) terminals is one of the practical and cost-effective solutions to the current challenges in exporting offshore natural gas where shuttle LNG carriers are used to transport the gas product.During manoeuvring LNG carriers in open sea at the vicinity of an FLNG terminal, operational hazards can have severe impacts on the safety of life, the environment and installations,particularly in bad weather conditions. For instance, during berthing operations in rough sea conditions, assisting tugboats may be insuf fi cient to pull the LNG carrier into a desired position. Therefore, the scenario of collision between the LNG and FLNG vessels is highly expected due to the short distance between the two vessels [2] . Better understanding of the hazards associated with different phases during ship manoeuvring will allow the development of criteria for the design of the whole system including the FLNG terminal, the LNG carrier,tugboats and of fl oading systems. Risk assessment studies are,therefore, required to evaluate the implications of operational risks and mitigation measures of FLNG terminals during ship manoeuvring.

There are various methods currently used for marine and offshore risk assessment which are classi fi ed into qualitative and quantitative approaches [3] . Qualitative approaches such as the risk matrix technique asses the risk in descriptive terms using expert opinions. Due to the limited knowledge and experience with the immature FLNG technology, the use of qualitative risk assessment techniques is often adopted by classi fi cation societies and maritime organisations [3–5] . In such techniques, experts from the LNG industry, offshore export systems and shipping industry decide on the degree of hazard usually based on their own experience in the fi eld [1] .In order to study a wide range of potential hazardous scenarios, experts often use Hazard Identi fi cation (HAZID) techniques in which the probability and consequence associated with a failure mode are weighted based on expert knowledge and combined by the risk matrix to obtain a risk index [3,6] .

The main drawbacks of the qualitative risk assessment techniques are time-consuming, expert knowledge dependent,and their results are often not reproducible. Human behaviour may also in fl uence the results of risk analyses resulting in an uncertain risk level. Furthermore, these techniques rely on the use of discrete attributes which do not account for uncertainty[7] .

Recently, the use of fuzzy logic based methods in arti ficial intelligence applications such as expert systems has been increasing. Fuzzy logic is a mathematical tool to model inaccuracy and uncertainty of the real world and human thinking in which variables have degrees of truthfulness or falsehood represented by a range of values between 0 (false) and 1(true). Unlike binary systems, the outcome of an operation is expressed as a probability in fuzzy logic systems. For example, an outcome may mean “probably true”, “possibly true”or “probably false”.

Fuzzy set approaches have been used in many engineering applications involving imprecise information such as the problem of air gap predictions in offshore platforms [8] , risk assessment of LNG carriers [7–9] , risk management of seaports and terminals [10] and expert systems [11] . Elsayed et al. [12] developed a fuzzy inference system to assess risks of LNG carriers during loading/of fl oading operations at terminals and found that the use of a fuzzy set approach is particularly suited for handling multiple attribute risk problems with imprecise data. Nwaoha et al. [13] developed a framework for the risks of hazards of LNG carrier operations using the combination of a risk matrix approach and a fuzzy evidential reasoning method. The fuzzy approach was used to synthesise the risk levels of the basic events to enable comparisons among top events. Stavrou and Ventikos [14] used a process mode and effects analysis approach to evaluate different risk scenarios related to ship-to-ship transfer of petroleum cargo operations. Zhao et al. [15] applied a Bayesian network method to assess the risks of accidents in the anchoring system of an LNG carrier. It is worth mentioning that neither of the aforementioned studies investigated risks of ship manoeuvring in open. Such situations during loading/unloading operations of LNG–FLNG vessels need to be assessed in terms of operational risks.

The scope of this work is to investigate several hazardous scenarios that could potentially occur during manoeuvring an LNG carrier in the vicinity of an FLNG terminal in normal and bad weather conditions. The outcome of HAZID study was obtained from [2] . To deal with the uncertainty in expert opinions, a fuzzy set approach which is based on a rule-based fuzzy model using Sugeno’s method for fuzzy inference was developed. Risk parameters were modelled using a number of fuzzy sets, and a fuzzy risk value was calculated for several hazardous scenarios at different phases during ship berthing operations. The fuzzy risk values obtained by the fuzzy set approach were compared with the results of the risk matrix technique.

2.Hazard identi fi cation (Hazid)

Prior to loading operations, the manoeuvring of an LNG carrier in open sea at the FLNG facility consists of a number of phases, and each phase can have multiple failure modes,i.e., potential hazards that can lead to undesirable consequences. In this work, 16 hazardous scenarios were considered as identi fi ed by experts in four different phases ( Table 1 ).Antão and Soares [2] performed an identi fi cation of the procedures of berthing and mooring in good and bad weather conditions. The primary risks are mainly related to operational risks during the berthing, loading/unloading, position keeping of both LNG and FLNG vessels and unberthing phases. The identi fi ed hazards are primarily caused by human errors or equipment failures. When performing a risk analysis and assessment, several main risks can be considered, i.e., risk to crew persons, to the environment, and to the economy and property. Risks for people (crews of both vessels performing mooring/unmooring procedures) and to the property (LNG and FLNG vessels) were covered in this analysis. As presented in Table 1 , the operational phases under investigation(denoted byS) includedS1 (pilot transfer and start of berthing approach),S2 (approach),S3 (berthing) andS4 (mooring).

Each hazardous scenario,Hij, was associated with a probability index (PI) and fi ve potential consequence indices (CI)for both normal and bad weather conditions where the numbers 1–5 denote the weight/severity of each consequence ( Table 2 ).

The fi ve potential consequences included Human Safety(HS), the Environment (E), Cargo/Monetary Loss (CML),Effect on Ship (ES), and 3rd party assets (A). The de fi nition of the probability levels is given in Table 3 whereas the consequence categories for human safety are presented in Table 4 . For instance,H11“failure of the system”during the pilot transfer phase in normal weather conditions was rated aslittleprobable(PI = 4) with aminorseverity for human safety (CI = 1 ➔1HS).

Table 1A summary of HAZID study of LNG–FLNG vessels during manoeuvring.

Table 2Assignment of probability and consequence indices.

3.Risk matrix approach

As previously mentioned, the risk matrix is a commonly used technique in formal safety assessments [3–5,17,18] ,which are rational and systematic processes for assessing the risks associated with shipping activity, and hence the results obtained by this technique can be served as a guideline to validate fuzzy risk values. The risk matrix combines the likelihood and severity in order to evaluate the risk level qualitatively using linguistic risk levels [3] . The risk matrix shown in Table 5 had a size of 8 × 5 (probability × consequence)in which the risk level is categorised as negligible “N”, low“L”, medium “M”and high “H”. The risk value obtained using this approach is the sum of PI and CI associated with each hazardHij[16] , for instance, the risk level due toH11“failure of the system”during the pilot transfer phase in normal weather conditions can be estimated asR= 4.0 + 1.0 = 5.0.

4.Rule-based fuzzy model approach

The Rule-Based Fuzzy Model (RBFM) developed for ship manoeuvring risk assessment is based onif–thenrules whichrepresent the relationship between the probability and consequence (inputs) and the outcome risk (output) of a hazardHij. In fuzzy logic, the crisp input value is converted into fuzzy inputs using membership functions. Fundamentally, a fuzzy logic system is divided into three steps: fuzzi fi cation,inference and defuzzi fi cation [19,20] .

Table 3De fi nition of probability index (PI) [16] .

Table 4De fi nition of consequence index (CI) for human safety, adopted from [16] .

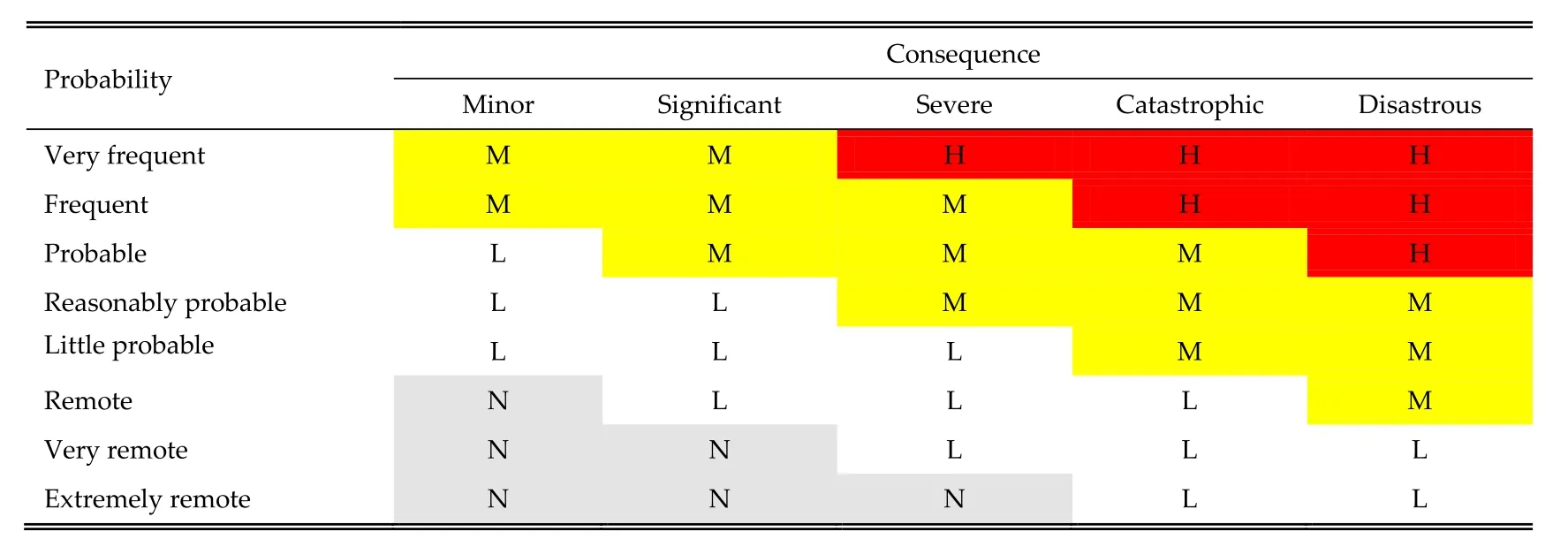
Table 5A typical multi-level risk matrix.

4.1. Fuzzi fi cation

In the fuzzi fi cation step, each crisp/fuzzy input into a fuzzy model may have multiple sets assigned to it. An input membership function can be generated by specifying a number;the degree of membership [0 –1], for each possible input value for a given label such as “frequent”and “minor”. A membership degree is a real number on [0, 1] such that the element does not belong to the set if the degree is 0; whilst the element belongs completely to the set if the degree is 1.

The fuzzi fi cation takes a real time input value and compares it with the stored membership function information so that the fuzzy input values can be produced. Different types of membership functions (denoted as MF) exist including,for instance, triangular, trapezoidal and Gaussian functions[21] . In this study, the triangular and Gaussian-type functions were tested to highlight the difference between these functions. Triangular membership functions were selected due to their simplicity, convenience of mathematical operations and effectiveness in representing judgment distributions of multiple experts [9,22] . The Gaussian membership functions were used by other researchers [ 7 , 17 ] and found to be suitable for risk assessment problems. The mathematical formulations of a triangular and Gaussian MF are given by Eqs. (1 ) and ( 2 ),respectively:

wherefA(x) is the membership function of a variablex, [a,b,c] are the elements of a set,mandσare the mean and the standard deviation, respectively. The parameters of eachmembership function tested are summarised in Table 6 for the probability and the consequence as denoted byPiandCi.Figs. 1 and 2 show the fuzzy sets ofPiandCirepresented by the triangular and Gaussian membership functions. For instance, the set ofP1“extremely remote”was assigned as (a,b,c) = (0, 1, 2) such that the central element of the triangular MF “b”was de fi ned to be equal to the index associated with the linguistic variable given in the risk matrix. On the other hand, the Gaussian MFs were then generated on the basis of the prede fi ned triangular MFs in whichm=bfor all fuzzy sets.In order to achieve a similar intersection between any two consecutive fuzzy sets for both triangular and Gaussian MFs, a standard deviationσof 0.425 was estimated and used for all fuzzy sets, as seen in Table 6 . As an example, this was illustrated in Fig. 3 forP2andP3such that atx= 2.5 a degree of membership functionfP(x= 2.5) = 0.5 was obtained for both triangular and Gaussian MFs which yieldsσ～0.425.

Table 6Parameters of membership functions used in modelling fuzzy sets.

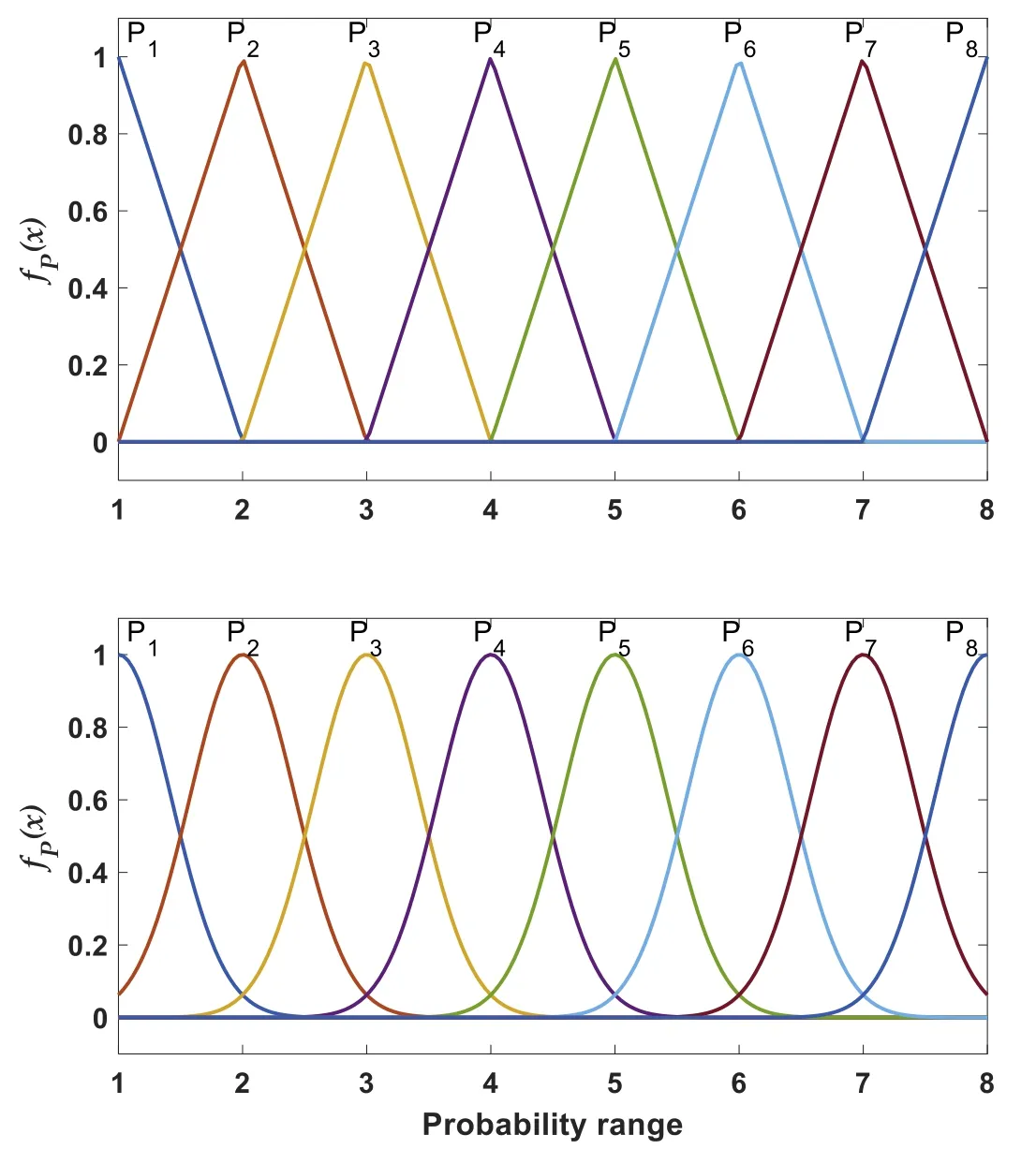
Fig. 1. Probability fuzzy sets using triangular MF (top) and Gaussian MF(bottom).

Fig. 2. Consequence fuzzy sets using triangular MF (top) and Gaussian MF(bottom).

4.2. Inference

In the present fuzzy model, a total number of 40if–thenrules were created based on the size of the risk matrix of 8 ×5. The precondition can consist of multiple conditions linked together withANDconjunction. The fi rst fi ve fuzzy rules which represent the fi rst row in the qualitative risk matrix given in Table 5 can be written as:

Fig. 3. The intersection of two fuzzy sets for probability indices P2 and P3 using triangular MFs (top) and Gaussian MFs (bottom).

Rule1:Ifprobability is “very frequent”andconsequence is “minor”thenrisk is “medium”.

Rule2:Ifprobability is “very frequent”andconsequence is “signi fi cant”thenrisk is “medium”.

Rule3:Ifprobability is “very frequent”andconsequence is “severe”thenrisk is “high”.

Rule4:Ifprobability is “very frequent”andconsequence is “catastrophic”thenrisk is “high”.

Rule5:Ifprobability is “very frequent”and consequence is “disastrous”thenrisk is “high”.

The computation of fuzzy rules, also known asfuzzyinference, was performed using the Sugeno fuzzy inference method [23] implemented in MATLAB. Elsayed [7] stated that the Sugeno method is computationally more ef fi cient and guarantees continuity of the fi nal risk output surface than the Mamdani method [24] . The fi rst-order Sugeno fuzzy model has rules of the form:

IfxisInput1andyisInput2thenz=px+qy+rwhereInput1and2are fuzzy sets which represent the probability and consequence of a failure mode, whilep,q, andrare the consequent parameters of the rule. The consequent parameters that result in the least performance index can be obtained by the least squares method for the given premise (input) parameters [23] . According to Sivanandam et al. [21] , higher order Sugeno fuzzy models may introduce signi fi cant complexity with little effect. It should be noted that when =q= 0, the above formula reduces to the zeroth-order which was adopted in this work for all calculations due to its simplicity whereris a crispy de fi ned constant representing the mean value ofthe associated range of risk levels given in Table 7 . Fig. 4 shows surface plots for risk matrices using the zeroth-order Sugeno fuzzy model for both triangular and Gaussian MFs in which the Gaussian MFs seem to produce a smoother surface than that was obtained by the triangular MFs.

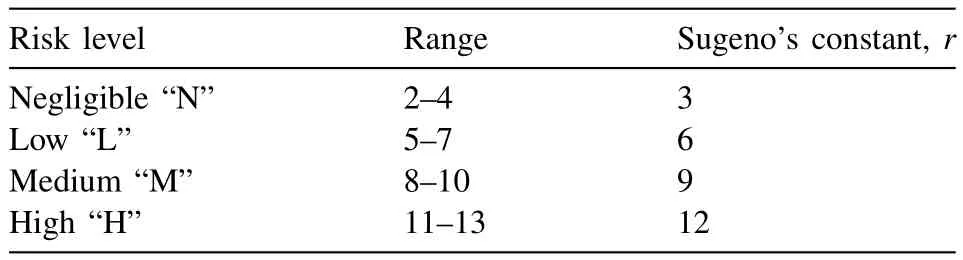
Table 7Sugeno’s constant, r , for risk levels.

The output level (z) of each rule is weighted by the fi ring strengthwiof the associated rule. For example, for anANDrule, the fi ring strength is obtained by:

wheref1(x)andf2(y)are the membership functions for inputsxandy, respectively.

4.3. Defuzzi fi cation

The fi nal output of the system is the weighted average of all rule outputs and computed as [21] :

whereNis the number of rules.

In order to compare the results obtained by the fuzzy set and risk matrix techniques, a risk index (RI) was used to combine the various consequence attribute risks into a uni fi ed risk measure:

Fig. 4. Surface plots for the output risk using triangular MF (top) and Gaussian MF (bottom).

whereMis the number of consequences,M= 5 in this case,ciis a weight factor, i.e., severity level for each consequence andRiis the risk value for each consequence attribute calculated from Eq. (4) for the fuzzy set techniques.

5.Results and discussion

The results of risk assessment of LNG–FLNG hazards during manoeuvring in normal and bad weather conditions are discussed below.

5.1. Risk values

Table 8 summarises the calculated RI values for the 16 hazardous scenarios in normal weather conditions. The RI values obtained by the fuzzy set approaches using triangular and Gaussian membership functions are denoted as TMF and GMF, whereas the results of the risk matrix technique are denoted by QRM.

It should be noted that the risk outcome values calculated by TMF and GMF were quite similar. Overall, the results of RI calculated by the rule-based fuzzy set techniques were found to be consistent with the results of the QRM technique which indicates that the relationship between risk parameters was correctly modelled in the fuzzy logic models usingif–thenrules. This can also be appreciated from Figs. 5 and 6 for normal and bad weather conditions, respectively. The Gaussian membership function was found to be more effective in risk ranking and more consistent with the QRM than the triangular membership functions tested. This can be attributed to the mathematical model of Gauss function being more effective in handling the range ofPiandCithan the triangular MF as illustrated in the surface plots shown in Fig. 4 . The hazards of the pilot transfer phase (H11–H15) imposed the highest risk level on all consequence attributes. It is worth mentioning that when the fi rst-order Sugeno model was attempted usingp=q= 1, a large variation was obtained in the results between fuzzy risk values and the QRM ones.

Fig. 7 shows a comparison of RI values between normal and bad weather conditions during the pilot transfer phase.Overall, as the assignments of expert opinions did not muchdiffer between the normal and bad weather conditions, the RI values were approximately similar for both conditions except for few hazards. For example, an increase of approximately 2.6% and 1% in RI values was obtained in bad weather conditions forH11“failure of the system”andH15“failure of the auto control system”, respectively.

Table 8Risk index (RI) results obtained by fuzzy set and risk matrix techniques for normal weather conditions.

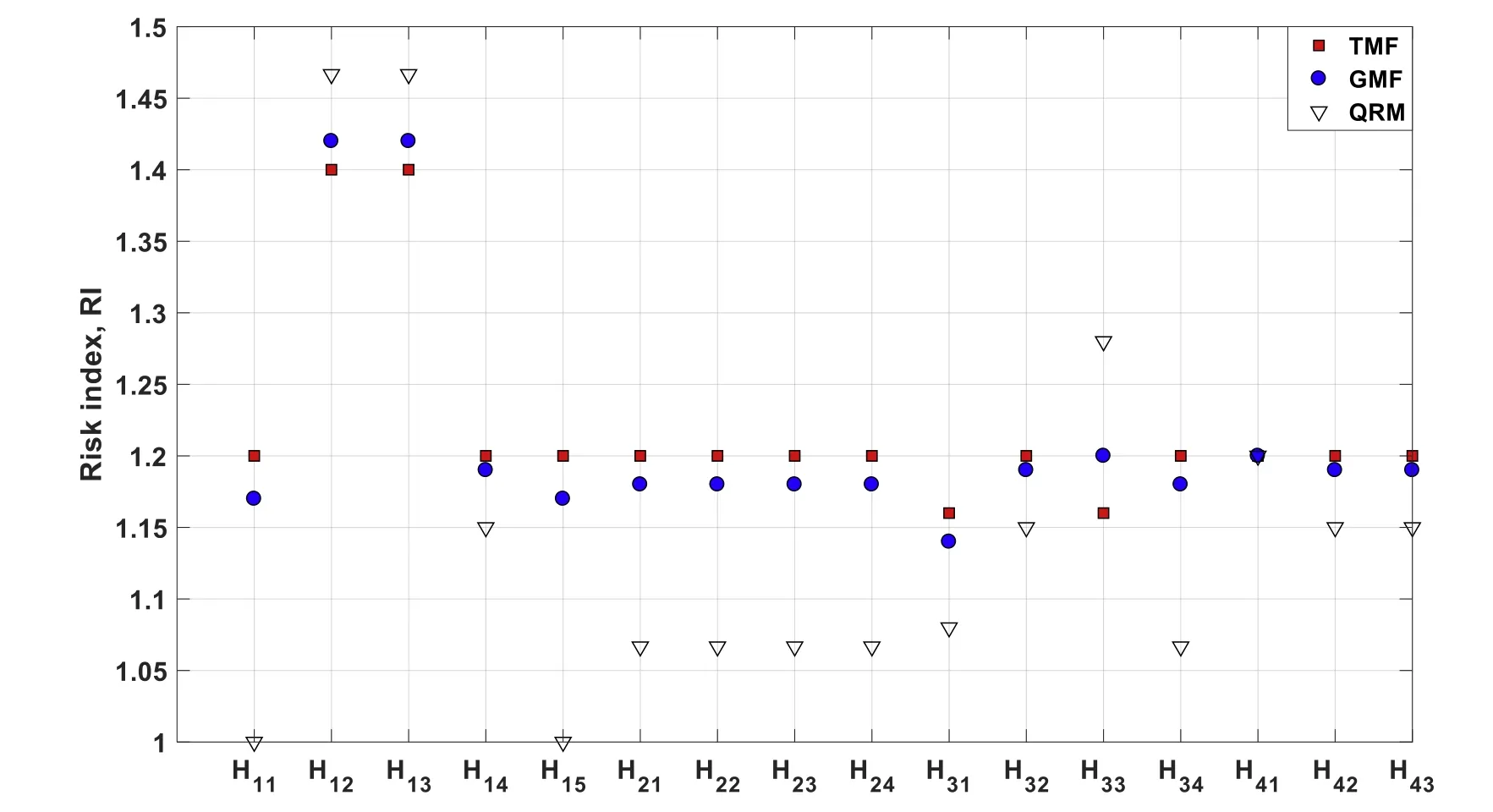
Fig. 5. Risk index results obtained by fuzzy set and risk matrix techniques for normal weather conditions.

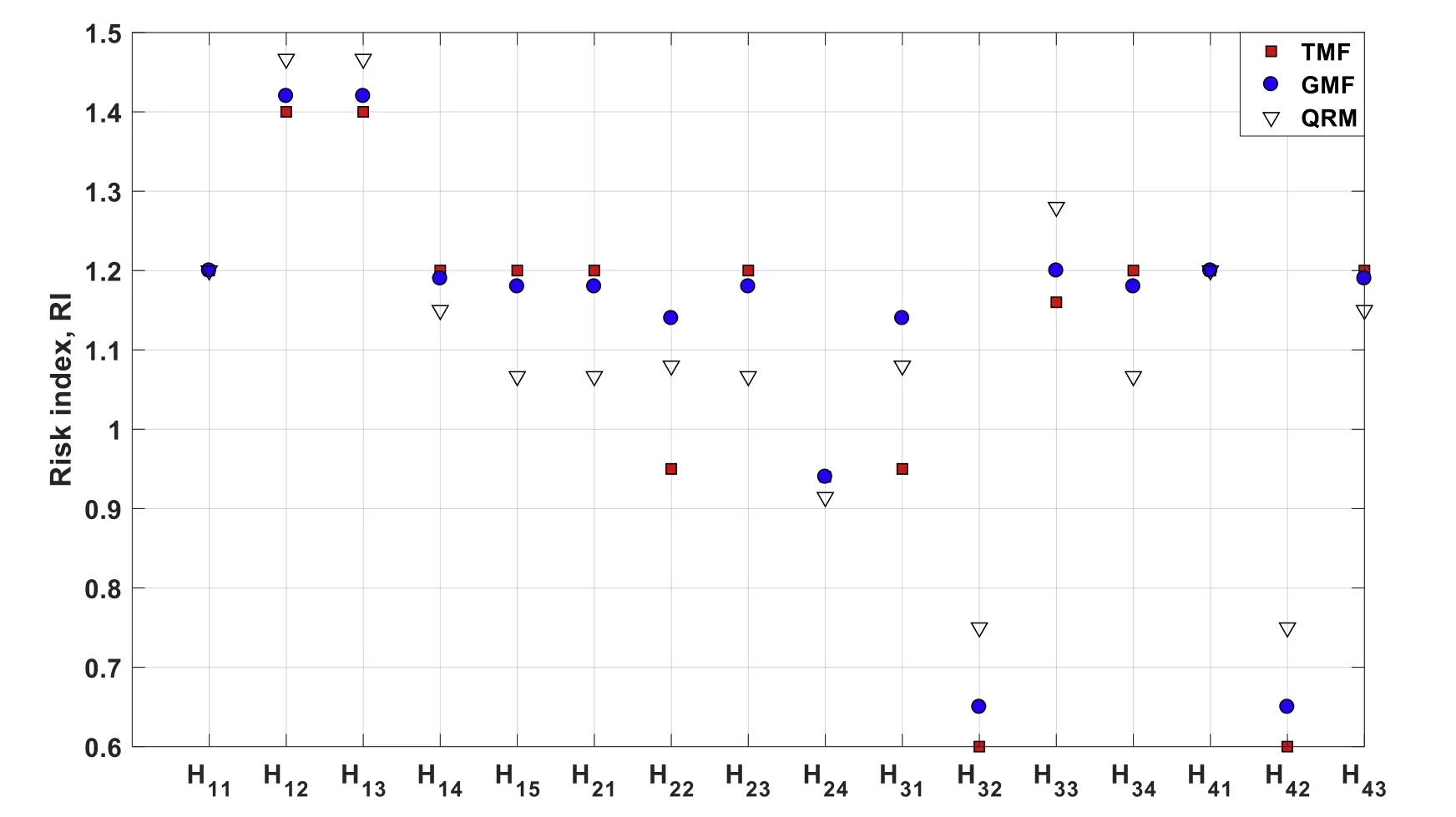
Fig. 6. Risk index results obtained by fuzzy set and risk matrix techniques for bad weather conditions.

5.2. Risk contributors

In order to identify the contribution of a hazard in the overall risk value imposed on the system during each operational phase, a risk pro fi le was obtained on the basis of RI values calculated by the Gaussian MF for bad weather conditions.During the pilot transfer phase, as shown in Fig. 8 , the failure of the pilot to board the LNG carrier and the failure of tugs to connect to the LNG carrier had similar risk contributions of 22% towards to the overall risk. During the approaching phase, as shown in Fig. 9 , the thruster failure of the FLNG vessel had the highest contribution of 27% followed by the failure of the pilot to suspend the approach with 26% towards to the overall risk. It should be stressed that the risks of dynamic positioning system must be thoroughly analysed in terms of its criticality on the operation of FLNG facilities during manoeuvring in open sea.

Fig. 7. Risk index results obtained by Gaussian MF for normal and bad weather conditions during pilot transfer.

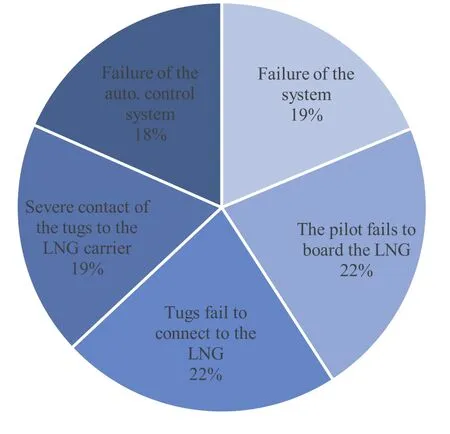
Fig. 8. Risk contributions of hazards during pilot transfer phase for bad weather conditions.

Fig. 9. Risk contributions of hazards during approach phase for bad weather conditions.

Fig. 10. Risk contributions of hazards during berthing phase for bad weather conditions.

Fig. 11. Risk contributions of hazards during mooring phase for bad weather conditions.

During the berthing phase, as shown in Fig. 10 , the hazard of collision of the LNG carrier to the FLNG vessel due to weather changes had the highest contribution of 29% followed by the failure of tugboats to control the approach rate with 28% towards to the overall risk. It should be noted that the hazards of collision and contact are the most critical failure modes during ship manoeuvring. As recommended by Østvik et al. [16] the scenario “collision”for LNG carriers should be prioritised in the risk analysis. For the mooring phase, as shown in Fig. 11 , the failure of the pneumatic line throwing device had the highest contribution of 40% followed by the energy of contact of the LNG carrier above limitations with 39% towards to the overall risk.

5.3. Sensitivity analysis

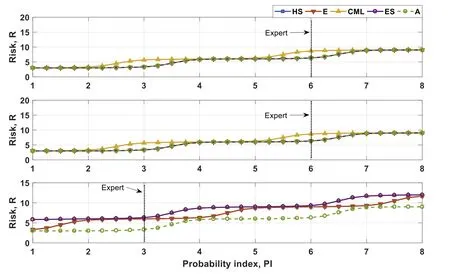
Fig. 12. Results of sensitivity analysis using the Gaussian MF for H12 (top), H13 (middle) and H33 (bottom).

Sensitivity analyses were conducted for the top-ranked three events includingH12“the pilot fails to board the LNG”,H13“tugs fail to connect to the LNG”andH33“collision of the LNG carrier to the FLNG vessel due to weather changes”.The effect of probability index was tested by varyingPivalues from 1–8 as shown in Fig. 12 where the values ofPiassigned by experts are denoted by vertical lines (Expert). Risk values(R) were found to increase with increasingPi, however, they were approximately constant over a certain range ofPi. For instance, the risk level associated withH12andH13increased with increasingPifor CML, but forPi= 1–2, 3–5 and 7–8 whereRvalue had approximately no change within these ranges. For both hazards, atPi＞6 which is assigned by experts, the risk value increased for all consequences except for CML such that the risk value exceeded the low level “L”given in the risk matrix ( Table 5 ). Similarly, for the hazardH33, the risk level increased with increasingPifor all consequence attributes. AtPi= 3, which is assigned by experts,the risk value for all consequences did not exceeded the low level “L”given in the risk matrix, however, asPiincreased the risk level associated with this hazard could exceed the medium “M”level or even the high level “H”. This indicates risk mitigations need to be provided by safety managers in case of increasing the likelihood of this scenario in order to reduce the risk level. Such fi ndings demonstrate the effectiveness of using fuzzy sets to model risk parameters and assist safety assessors in risk evaluation.

6.Conclusions

Manoeuvring of a Lique fi ed Natural Gas (LNG) carrier in open sea at Floating LNG (FLNG) terminals can be associated with operational risks of potential consequences to human safety, the environment and economy. A fuzzy set approach was developed in this paper to handle the uncertainty in expert opinions used for qualitative risk assessment studies.Risk parameters were modelled by fuzzy sets, and a fuzzy risk value was calculated for several hazardous scenarios at different phases during ship berthing operations. Based on the fi ndings presented in this paper, the following conclusions were drawn:

·Fuzzy set approaches used in this work provided quantitative risk values for several hazardous scenarios at different phases of berthing operations at FLNG terminals.The results of risk index obtained by rule-based fuzzy set techniques were found to be consistent with results of the qualitative risk matrix technique. As the use of the risk matrix technique has been common in practice for formal safety assessments by classi fi cation societies and IMO [ 3 –5 ], the results obtained by this technique were used to validate fuzzy risk values. The overall agreement between the two techniques indicated that the relationship between risk parameters was correctly modelled in the fuzzy logic models based on if–then rules.

·The rule-based fuzzy set techniques enabled users to conduct sensitivity analysis for risk parameters which demonstrate the effectiveness of using fuzzy sets to assist safety assessors during risk evaluation.

·The hazards of the pilot transfer phase imposed the highest risk level on all consequence attributes. It is, therefore,recommended that safe pilot transfer from an offshore gas terminal to LNG carriers and vice versa should be conducted using a safe procedure for pilot transfer arrangement. Hazards of collision and contact need also to be further investigated.

[1] E. Aronsson , FLNG compared to LNG carriers-requirements and recommendations for LNG production facilities and re-gas units Masters Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2012 .

[2] P. Antão , C.G. Soares , Maritime Engineering and Technology, Taylor &Francis Group, London, UK, 2012, pp. 425–432 .

[3] ABS, Guidance Notes on Risk Assessment Applications for the Marine and Offshore Oil and Gas Industries, American Bureau of Shipping,Houston, USA, 2000 Shipping ABo, editor.

[4] E. Vanem , P. Antão , I. Østvik , F.D.C. de Comas , Reliabil. Eng. Syst.Safety 93 (2008) 1328–1344 .

[5] DNV. Recommended practice DNV-RP-F107: Risk assessment of pipeline protection. Høvik, Norway: Det Norske Veritas, DNV; 2010.

[6] J. Spouge , A Guide to Quantitative Risk Assessment for Offshore Installations, CMPT, 1999 .

[7] T. Elsayed , Appl. Ocean Res. 31 (2009) 179–185 .

[8] N. Abdussamie , W. Amin , R. Ojeda , G. Thomas , Y. Drobyshevski , in:Proceedings of the Nineteenth Australasian Fluid Mechanics Conference, Melbourne, Australia, AFMS, 2014 .

[9] T. Elsayed , K. Marghany , S. Abdulkader , Ships Offshore Struct. 9(2014) 355–364 .

[10] K. Mokhtari , J. Ren , C. Roberts , J. Wang , Expert Syst. Appl. 39 (2012)5087–5103 .

[11] C. Samantra , S. Datta , S.S. Mahapatra , Expert Syst. Appl. 41 (2014)4010–4022 .

[12] T. Elsayed , H. Leheta , M. Shehadeh , Ships Offshore Struct. 4 (2009)127–131 .

[13] T.C. Nwaoha , Z. Yang , J. Wang , S. Bonsall , Ocean Eng. 72 (2013)31–44 .

[14] D.I. Stavrou , N.P. Ventikos , J. Risk Res. 19 (2016) 913–933 .

[15] S. Zhao , C.G. Soares , H. Zhu , in: Proceedings of the 2015 International Conference on Transportation Information and Safety (ICTIS), IEEE,2015, pp. 432–436 .

[16] Østvik I., Vanem E., Castello F. HAZID for LNG tankers. SAFEDOR Report D. 2005; p. 4.

[17] T. Elsayed , H. Leheta , I. Belhaj , Proc. Inst. Mech. Eng. Part M J. Eng.Maritime Environ. 225 (2011) 171–180 .

[18] J.E. Vinnem , Offshore Risk Assessment Principles, Modeling and Applications of QRA Studies, Springer, London, 2007 .

[19] J. Zeng , M. An , N.J. Smith , Int. J. Project Manag. 25 (2007) 589–600 .

[20] J.M. Mendel , Proc. IEEE 83 (1995) 345–377 .

[21] S. Sivanandam , S. Sumathi , S. Deepa ,Introduction to Fuzzy Logic Using MATLAB, Springer, 2007 .

[22] A. Mentes , I.H. Helvacioglu , Expert Syst. Appl. 39 (2012) 3283–3297 .

[23] T. Takagi , M. Sugeno , IEEE Trans. Syst. Man Cybern. (1985) 116–132 .

[24] E.H. Mamdani , S. Assilian , Int. J. Man Mach. Stud. 7 (1975) 1–13 .