Thenewtypesofwavesolutionsofthe Burger’s equationandthe Benjamin–Bona–Mahonyequation

Md. Azmol Hud M. Ali Akr Shewli Shmim Shnt

a Mathematics Discipline, Khulna University, Bangladesh

b Department of Applied Mathematics, University of Rajshahi, Bangladesh

c Department of Mathematics, University of Rajshahi, Bangladesh

1.Introduction

Many of the principles of natural phenomena or underlying behavior of the natural world can be described by the statements or relations where rate of changes is involved.These rates can be expressed in mathematical relations that in turn emerge linear or nonlinear ordinary differential equations(ODEs) or partial differential equations (PDEs). For instance,in physics, the equation of heat fl ow and wave propagation model; in ecology, the population model; in chemistry dispersion reaction model and so on. These models are governed by linear or nonlinear ODE or PDE. Generally, most of the real incidents that appear in our daily life are inborn nonlinear. As a consequence, nonlinear partial differential equations(NPDEs) have been the subject of study and research interest in various branches of science and engineering. Building, solving and analyzing different mathematical models and derivation of its solutions are rich and important topics in the literature of NPDEs. Particularly, the analytical solutions are important to understand the mechanism and physical effects through the model problem. It provides the crucial qualitative and quantitative information about the underlying behavior of the model in a direct way. Moreover, it is useful to validate the numerical method. Thereby, it is important to be familiar with all existing, traditional and recently developed methods for constructing exact solutions and to extend or discover new methods for further research. But, due to human limitations involved in compiling computational algorithms for solving differential equations symbolically to fi nd an exact solution are not a straightforward work, and intrinsically a daunting task. However, the arrival of work-station or mainframe computer platforms with highly computational mathematical software with built in graphing utility packages like as Maple, Mathematica, Matlab etc. has paved the way to overcome these formidable obstacles and enhanced further develop, extension in the theory and applications of NLEEs and subsequently for searching different methods for extracting new exact solutions. Some of the references herein are mentioned.

In the literature, many approaches for obtaining exact solutions of nonlinear equations have been presented, videlicet;Ma et al. [1] introduced the Frobenius integrable decomposition for solving a class of partial differential equations that possesses speci fi ed Frobenius integrable decompositions. The stated method is illustrated by the KdV and potential KdV equations. Explicit exact solutions of generalized KdV equation are also determined by Ma and Zhou [2] . Ma and You applied the variation of parameters method for solving nonhomogeneous partial differential equations that consist of system of linear partial differential equations whose Wronskian determinant solves the KdV equation in bilinear form [3] .Mohyud-Din et al. [4] , applied He’s polynomials method for investigating solitary wave solutions of seventh order generalized KdV equation and suggested that the solutions of nonlinear problems can be obtained without discretization,linearization or any boundary value problems [4] . They also used the variational iteration method [5] to investigate the partial differential equations. Noor et al. [6–9] , applied the expfunction method to construct the traveling wave-soliton type solutions of different nonlinear equations, such as, Fitzhugh Nagumo and Calogero–Degasperis–Fokas equations. Dehghan[10] applied the exp-function method to examine the partial differential equations. Ma [11] studied the exact solutions of the KdV equation introducing complexition solutions that is derived from the Wronskian determinants of eigenfunctions of the Schrodinger spectral problem associated with complex eigenvalues. The results showed that the solutions possess singularities of combinations of trigonometric function waves and exponential function waves with different traveling speeds. Toda lattice equation [12–14] is also studied in different forms, such as, complexiton and rational solutions in Casoratian form by Ma et al.

Biswas et al. [15] studied extensively the Benjamin–Bona–Mahoney (BBM) equation by transforming into the combined KdV-mKdV equation with power law nonlinearity. They studied this combined equation from the point of view of Lie group theory and derived the Lie point symmetry generators of this combined equation. A number of exact group-invariant solutions of the BBM equation are obtained by using the Lie point symmetries of the equation by symmetry reduction.Biswas [16] found an exact 1-soliton solution of the BBM equation, with dual-power law nonlinearity where the solitary wave ansatz is used to carry to solve the equation. Dual power-law is applied in hybrid Benjamin–Bona–Mahoney–Burger’s equation by Biswas et al [17] . In Ref. [17] , three different techniques, the ansatz method, Lie-symmetry analysis and the (G′/G)-expansion method are used to fi nd shock wave solutions. The nature of the solutions is also discussed by them which are obtained in different methods. The perturbation theory is applied to the BBM equation by Biswas and Konar [18] . Wang et al. [19] applied Lie symmetry analysis of group theory to obtain the solution of (2 + 1) dimensional coupled Burger’s equations. By using the ansatz method they found many exact solutions of Burger’s equation. Moreover,Painleve truncated expansions are used to derive new exact bell-type solutions. The 1-Soliton solutions of the generalized Burger’s equation and extended to (2 + 1) dimensions with full nonlinearity have been studied by Biswas et al. [20] . Jawad et al. [21] studied the complex solutions of family of Burger’s equation by means of the tanh method. Biswas et al. [22] use the perturbation theory to obtain the solitary waves solutions and Jacobi elliptic function method to obtain the solutions of Bona–Chen equation. In Ref. [23,24] Biswas et al. obtain the two and three soliton solutions of the nonlocal Boussinesq equation by simplifying Hirota method. Biswas et al. [25] and Antonova and Biswas [26] implemented Jacobi’s elliptic function expansion method to obtain soliton and other periodic singular solutions of Benjamin–Bona–Mahony and Nizhnik–Novikov–Veselov equations. Bhrawy et al. [27] obtained the soliton solution of the Gear-Grimshaw model following with the power law nonlinearity and some interesting solutions of this model are extracted by the F-expansion method. Biswas and Ismail [28] also found the 1-Soliton solution of the coupled KdV equation and Gear-Grimshaw model by power law nonlinearity. Very recently, Biswas et al. [29] , studied shallow water waves that are described by the Boussinesq equation having logarithmic nonlinearity, where the traveling wave hypothesis is applied to obtain Gaussian solutions. Also in recent times [30–34] , much work on dispersive shallow water waves, dispersive long wave in fl uids have been done.

Different numerical methods, such as, fi nite difference, finite element, meshless approach, homotopy perturbation technique have been studied by Mohyud-Din et al. [35–37] to solve the fi fth order KdV equation and improved Boussinesq equations. Dehghan et al. [38,39] , found the numerical solu-tion of nonlinear higher dimensional generalized Benjamin–Bona–Mahony–Burger’s equation via the meshless method of radial basis functions and interpolating the element free Galerkin technique. Sheikholeslami et al. [40–47] investigated numerical solution of nonlinear partial differential equations widely in the fi eld of fl uid dynamics. Also different numerical approaches as for example fi nite element method is also applied in the fi eld of nano fl uid intensively by them [48–57] .

In 2008, Wang et al. [59] proposed a new approach to extract nonlinear PDEs called (G′/G)-extension method. After two years, in 2010 Li et al. [60] introduced the (G′/G, 1/G)-expansion method which is an extension of Wang et al.’s method to search the nonlinear Zakharov equation. Yet, this extended method has not been not used to search huge amount of other nonlinear evolution equations. In this article, our endeavor is to test the applicability of (G′/G, 1/G)-extension method to the Burger’s and BBM equations and searching new and further general wave solutions.

The rest of this article is sorted out as follows: In Section 2 , the (G′/G, 1/G)-expansion method is described. In Section 3 , the Burger’s and the Benjamin–Bona–Mahony equations are chosen to illustrate the applicability of the introduced method. Results and discussion are given in Section 4 . Finally conclusion is given in Section 5 .

2.Analysis of the two variable (G ′ /G , 1/G ) -expansion method

Herein, the main steps of the (G′/G, 1/G)-expansion method are illustrated succinctly. Before discussing the main steps of this expansion method to dig up traveling wave solutions to NLEEs, some interpretations are required. Li et al. [60] have summarized this expansion method with the following remarks:

Remark 1.At the beginning, we consider the second order liner ordinary differential equation (LODE)

and for straightforwardness herein and after, we use

By means of ( 2.1 ) and ( 2.2 ), we obtain

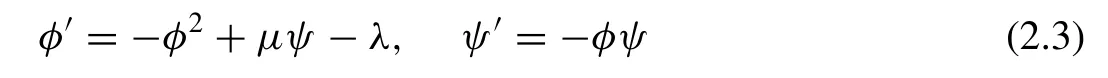
The form of the general solutions of ODE ( 2.1 ) depend upon the parameter whetherλ＜0,λ＞0 orλ= 0.

Remark 2.Ifλ＜0, the general solution of the LODE ( 2.1 )is

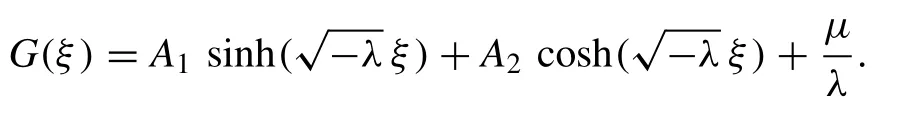
From which the following relationship can be established

whereA1andA2are two arbitrary constants and

Remark 3.Ifλ＞0, the general, solution of Eq. (2.1) has the form

and hence it can be easily found

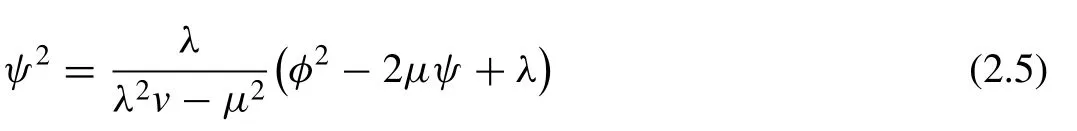
whereA1andA2are two arbitrary constants and

Remark 4.Ifλ= 0,the general solution of Eq. (2.1) isG(ξ)

and after some calculations, it can be deduced

whereA1andA2are two arbitrary constants.

At this phase, we consider a general NLEE involving two independent variables, videlicet the temporal variabletand spatial variablexof the form

where in, the left-hand side of ( 2.7 ) is a polynomial inu(x,t) and its partial derivatives in which higher order derivatives and nonlinear terms are involved. In order to examine the Eq. (2.7) by using (G′/G, 1/G)-expansion method the following steps are to be considered.

Step 1 :First, we introduce the wave variableξ=x-ct,so thatu(x,t)=u(ξ)and use the following relations

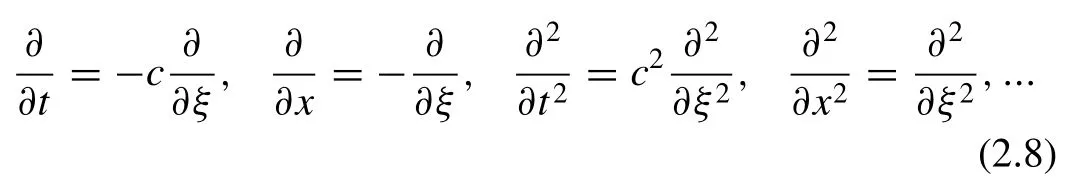
and so on for other derivatives. These operators change ( 2.7 )into an ODE as follows:

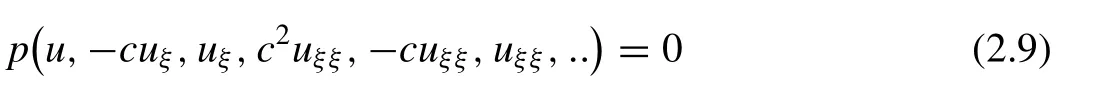
whereuξ,uξξ,uξξξand so on denote derivatives ofuwith respect toξ. Next, integrating Eq. (2.9) as many times as possible and set the arbitrary constants of integration to zero.

Step 2:Suppose that the general solution of the Eq. (2.9) can be expressed by a polynomial inφandψin the formal form as

whereφ=G′/G,ψ= 1/GandG=G(ξ)satis fi es the second order LODE ( 2.1 ),ai(i= 0,1,2,...,N),bi(i= 0,1,2,...,N),c,λandμare constants to be determined later on. Moreover, the positive integerNcan be determined by using the homogenous balance process between the highest order derivatives and the nonlinear terms appearing in ( 2.9 ).

Step 3 :Asu(ξ) is a solution of Eq. (2.9) , substituting ( 2.10 ) into ( 2.9 ), using ( 2.3 ) and ( 2.4 ) (or using ( 2.3 ),( 2.5 ) and ( 2.3 ), ( 2.6 )) the left side of ( 2.9 ) transforms into a polynomial inφandψ, where in the degree ofψis not greater than one. Vanishing each coef fi cient of the polynomial inφ,ψto zero yields a system of algebraic equations inai(i= 0,1,2,...,N),bi(i= 0,1,2,...,N),c,λ(λ＜0),μ,A1 andA2 .

Step 4 :Solving the algebraic equations derived in Step 3 with the aid of software with symbolic computing facilities like, Maple or Mathematica and inserting the obtained values ofai(i= 0,1,2,...,N),bi(i= 0,1,2,...,N),c,λ,μ,A1andA2into ( 2.10 ), one can obtain the traveling wave solutions revealed by the hyperbolic functions of Eq. (2.9) (or can be expressed by trigonometric function ifλ＞0 and rational function ifλ= 0).

3.Formulation of the solutions

3.1. The Burger’s equation

In this section, we consider the Burger’s equation [19–21] ,in normal form which is de fi ned by

The Burger’s equation describes one-dimensional internal waves in deep water. This equation arises in the propagation of internal waves in a strati fi ed fl uid of considerable depth,as for instance, a double layer fl uid in which a shallow upper layer sits on top of a deep lower layer.

By means of the traveling wave variable

wherecis the celerity of the traveling wave that is to be determined later, the NLEE ( 3.1.1 ), now converts into an ODE in the independent variableξ

Integrating it with respect toξ, yields

where the integration constant is taken zero.

In accordance with to step 2, balancing the highest order derivatives and nonlinear terms, we attain

Substituting the value ofNinto Eq. (2.10) , delivers

Case1: Whenλ＜0 (Hyperbolic function solutions)

Substituting the value ofuand its derivatives into Eq.(3.1.4) along with( 2.3 )and ( 2.4 ), the left hand side of ( 3.1.4 )becomes a polynomial inφandψ. Setting each coef fi cient of this polynomial equal to zero, a system of algebraic equations is found as follows:

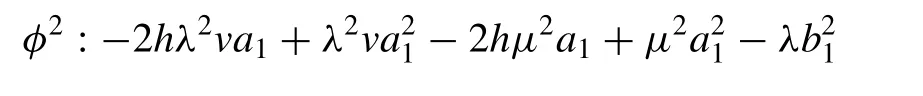
Substituting the above values into ( 3.1.6 ), together withφ=(G′/G)andψ=(1/G), we obtain

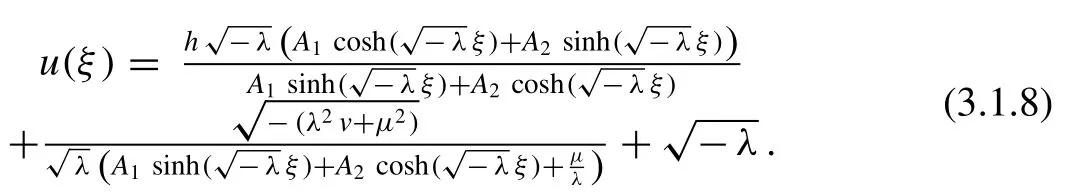
wherev=-andλ＜0.

In particular, whenA1= 0,A2/= 0 andμ= 0, we attain the solution of Eq. (3.1.1) as follows:

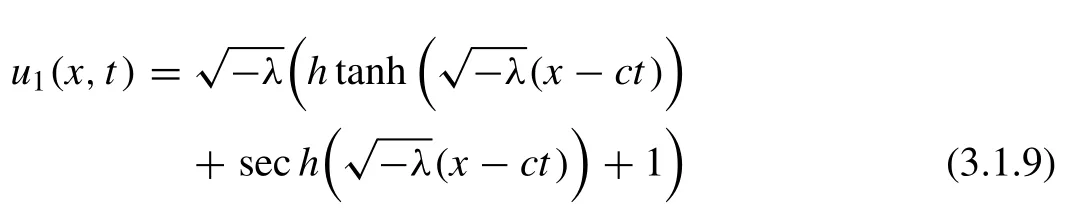
On the other hand, whenA1/ = 0,A2= 0 andμ= 0, we attain the subsequent travelling wave solution of Eq. (3.1.1) :

SinceA1andA2are arbitrary constants, the other selection of their values provide much new and further general solutions to the Burger’s equation, but to avoid the monotonous the rest of the solutions are not documented here.

Case2: Whenλ＞0 (Trigonometric solutions)

Similar tocase1, substituting the value ofuand its derivatives into Eq. (3.1.4) , along with ( 2.3 ) and ( 2.5 ), the left hand side of ( 3.1.4 ) converts into a polynomial inφandψ. Equating each coef fi cient equal to zero, a system of algebraic equations can be found and solving them with the help of Maple,we obtain (for conciseness and simplicity the algebraic equations are not given)

By means of these values from Eq. (3.1.6) , together withφ=(G′/G)andψ=(1/G), we achieve

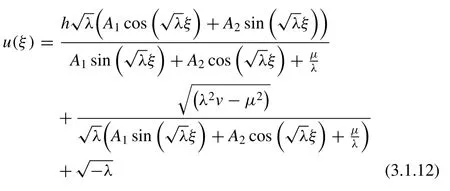
Computing the parallel course of algorithm of case 1, we obtain the solution of Eq. (3.1.1) whenA1= 0,A2/ = 0 andμ= 0,as

2017年10月2日， 比利时向欧盟委员会通告全面禁止塑料微珠用于消费品中的草案，通告中指出将自愿淘汰所有消费品中的微塑料，其“部门禁令”最初将适用于化妆品和牙膏，以及后来的清洁和保养产品、粘合剂和胶粘剂[14]。目标是到2019年实行在所有一次性化妆品和牙膏中使用塑料微珠的“全面禁令”。该计划草案得到了联邦能源，环境和可持续发展部等的赞同。

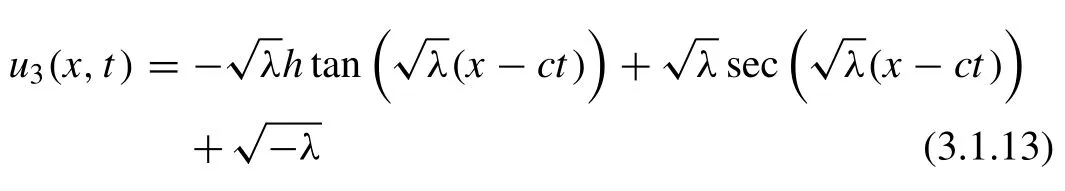
For the particular case, whenA1/ = 0,A2/ = 0 andμ= 0, we achieve the travelling wave solution of Eq. (3.1.1) as

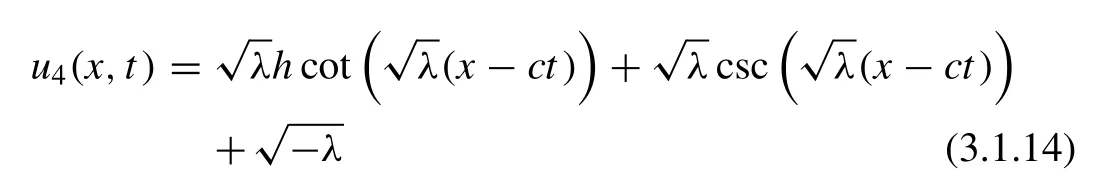
Case3: Whenλ= 0(Rational function solutions)

Similar to thecase1, by means of the value ofuand its derivatives from Eq. (3.1.4) , along with ( 2.3 ) and ( 2.6 ), can be obtained a polynomial inφandψ. Vanishing each coef fi cient of the polynomial yields a system of algebraic equations and solving them with the aid of Maple, we get (for brevity and simplicity algebraic equations are not given)

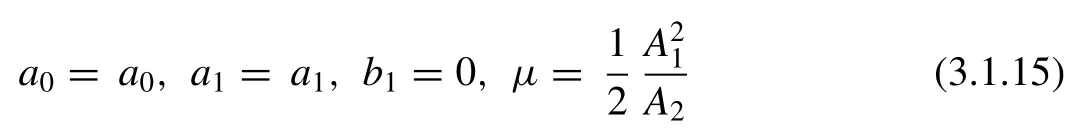
where,A1andA2are two arbitrary constants. Inserting the values of the constants into Eq. (3.1.6) together withφ=(G′/G)andψ=(1/G), we attain

where,A1andA2are arbitrary constants. It is important to note that the wave solutionsu1(x,t) tou5(x,t) of the Burger’s equation are resourceful and were not found in the earlier studies. The above solutions might be fruitful to scrutinize the one-dimensional internal waves in deep water.

3.2. The Benjamin–Bona–Mahony equation

The Benjamin–Bona–Mahony equation (BBM) [38,39]

is derived from the regularized long-wave equation

by considering the particular value of the constantsa= 1 andb= 1 . This equation was studied by Benjamin, Bona and Mahony as an improvement of the Korteweg–de Vries (KdV)equation

ut+auux+uxxx= 0,

by replacing the third order derivativeuxxxby a mixed derivativeuxxt, for modeling unidirectional propagation of weakly long dispersive waves in inviscid fl uids [33-34] . This change leads the BBM equation in a bounded dispersion relation,whereas the KdV equation results an unbounded dispersion relation. Prior to this, in 1966 it was introduced by Peregrine, in the study of undular bores. Nowadays, this equation is used to model the surface waves of long wavelength in liquids, acoustic waves in an harmonic crystals, acoustic-gravity waves in compressible fl uids, hydromagnetic waves in cold plasma and so on. Having been wide applicability of the BBM equation in different arena of physical science, it has attracted a considerable amount of attention to the researchers.

The travelling wave variableu(x,t)=u(ξ),ξ=x-ct,allows us in converting Eq. (3.2.2) into an ODE foru=u(ξ):

Integrating this equation with respect toξonce and setting up the arbitrary constant equal to zero, we obtain

Balancing the nonlinear termu2and highest derivativeu′,occurring in ( 3.2.4 ), delivers

Thus, for this value ofN, Eq. (2.10) becomes

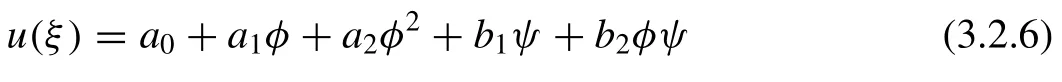
Now depending on the sign of the values ofλassorted solutions, videlicet the hyperbolic, trigonometric and rational function solutions can be found.

Case 1 :Whenλ＜0 (Hyperbolic function solutions)

Substituting the value ofufrom ( 3.2.6 ) and its various derivatives into ( 3.2.4 ) along with ( 2.3 ) and ( 2.4 ) the left hand side of Eq.( 3.2.4 ) becomes a polynomial inφandψ. Equating each coef fi cient of this equation to zero yields a system of algebraic equations given below:

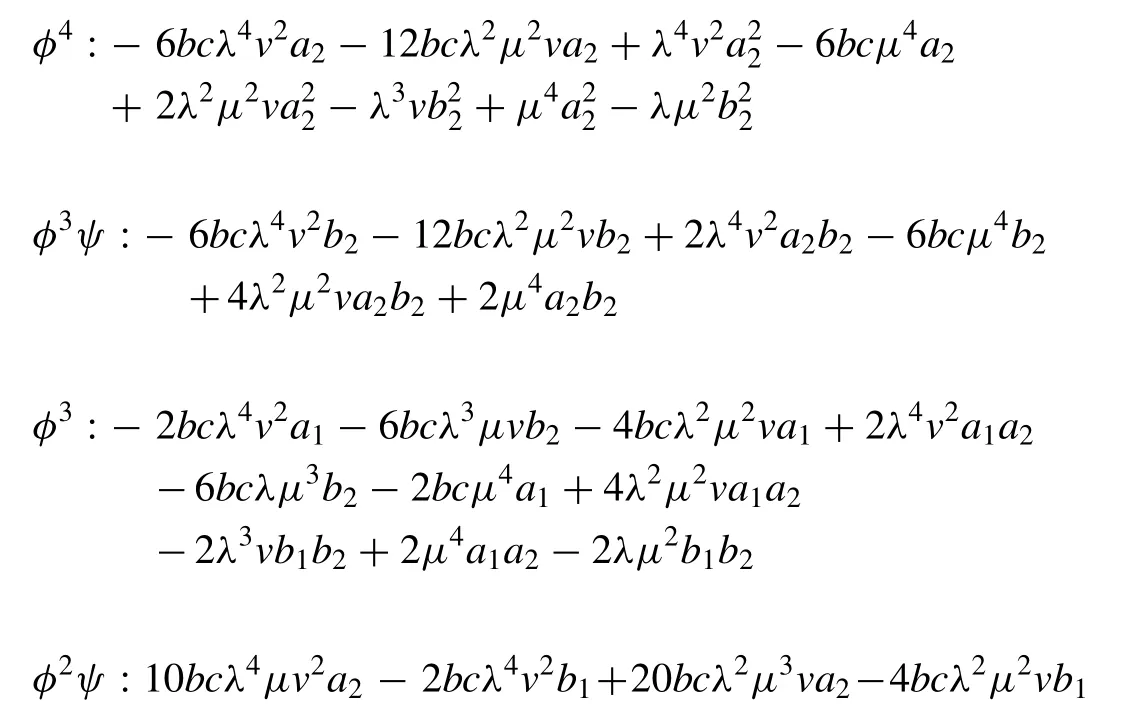
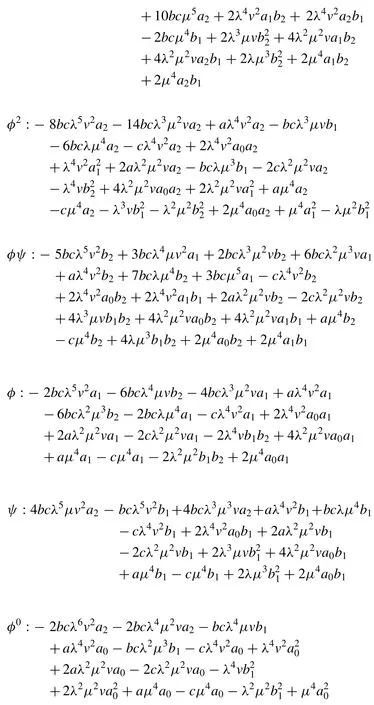
Solving the above system of equations with the aid of Maple or Mathematica, we attain two sets of solution:

Solutionset1:

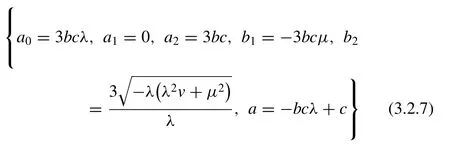
Inserting the values of the constants into solution ( 3.2.6 ),we achieve the subsequent wave solution

wherev=-λ＜0 andλ2v+μ2＞0.

In particular, if we setA1= 0,A2/= 0 andμ= 0 into the solution (3 .2.8) , we obtain following wave solution

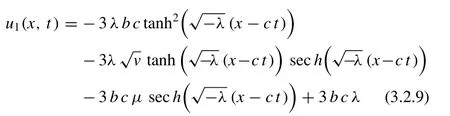
whereξ=x-ct.

Again, if we setA1/ = 0,A2= 0 andμ= 0 into the solution ( 3.2.8 ), we obtain next wave solution

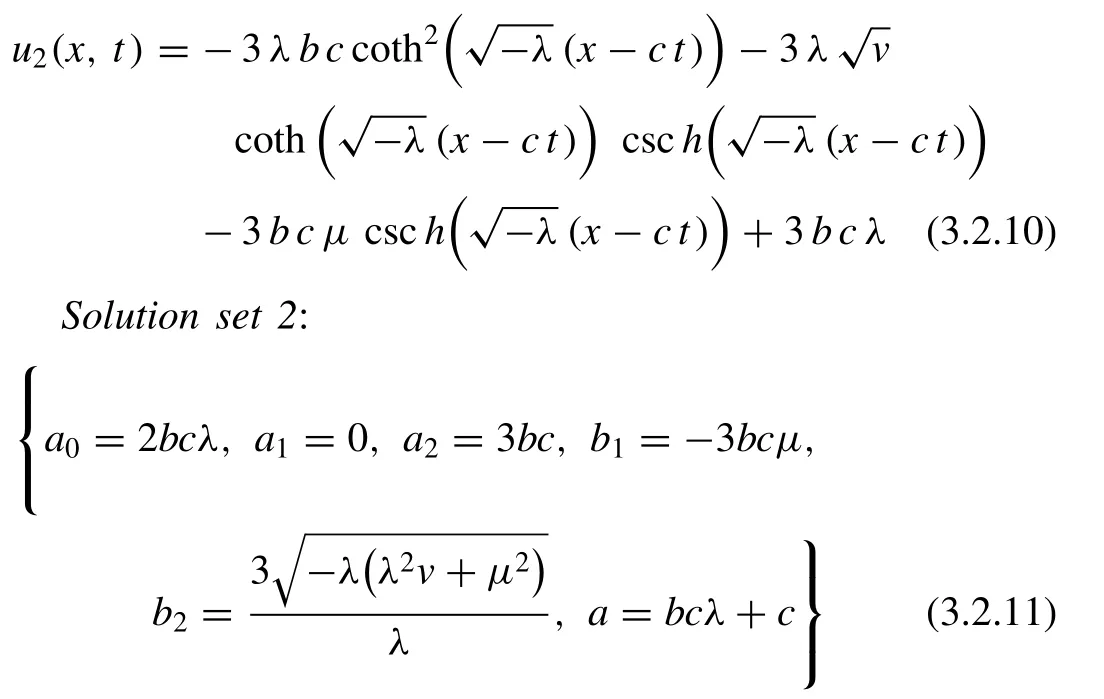
Substituting these values into solution Eq. (3.2.6) , we obtain the solution in the following shape

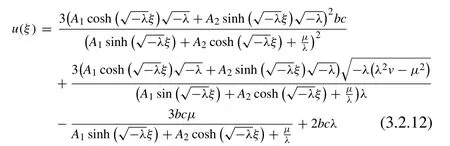
If we putA1= 0,A2/ = 0 andμ= 0 into ( 3.2.12 ), the subsequent wave solution is obtained

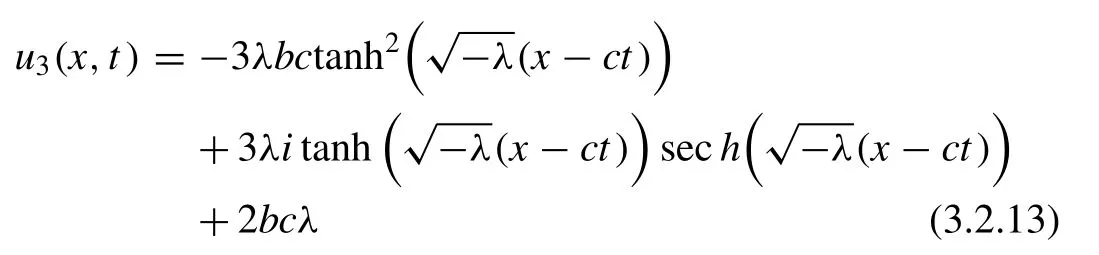
Likewise, if we putA1/ = 0,A2= 0 andμ= 0 into ( 3.2.12 ), we extract the following wave solution

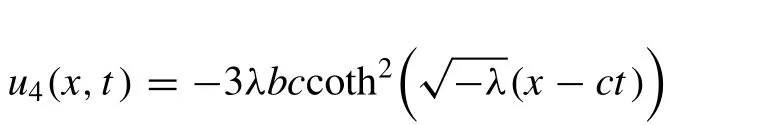
Case 2 :Whenλ＞0 (Trigonometric function solutions)

Using the values ofu(ξ) and its different derivatives into Eq. (3.2.4) along with ( 2.3 ) and ( 2.5 ) the left hand side of Eq. (3.2.4) turns into a polynomial inφandψ. Setting the value of each coef fi cient of this polynomial equation to zero yields a system of over-determined set of algebraic equations(herein for conciseness and simplicity the algebraic equations are not given) and solving them the value of constants are found:

Solutionset1:

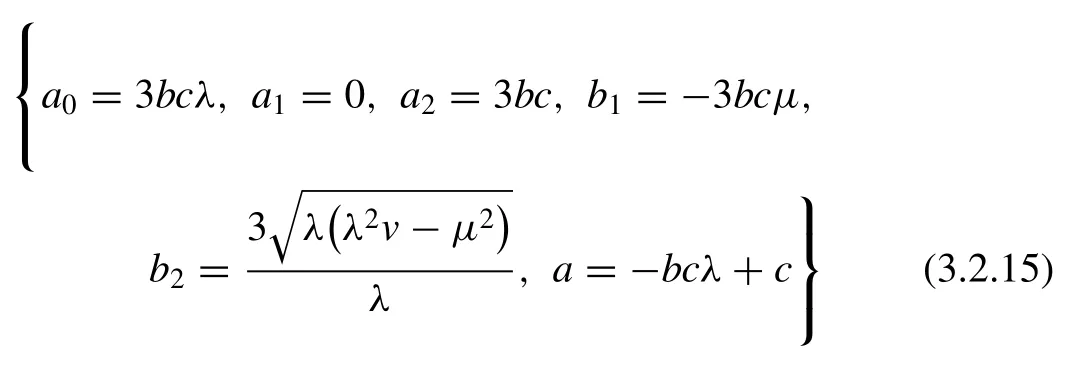
By means of these values, from ( 3.2.6 ) together with ( 2.2 )and ( 2.5 ), we obtain the succeeding wave solution

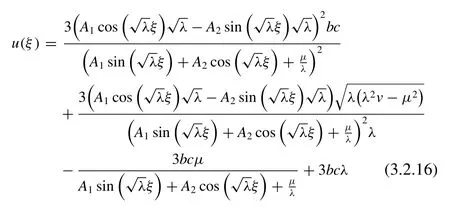
Setting the de fi nite valuesA1= 0,A2/ = 0 andμ= 0 into( 3.2.16 ), we obtain the wave solution

On the other hand, setting the de fi nite valuesA1/ = 0,A2=0 andμ= 0 into ( 3.2.16 ), we obtain the wave solution

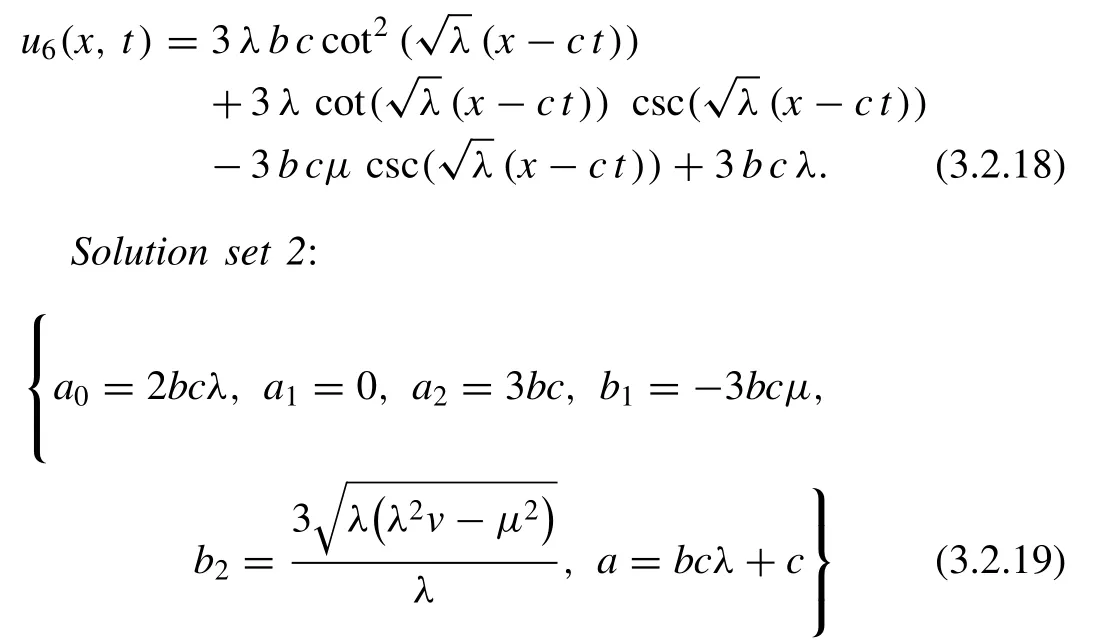
In the similar way, if we substitute the above values into( 3.2.16 ) along with the added conditionA1= 0,A2/ = 0 andμ= 0, we obtain another wave solution

Alternatively, if we substitute the above values into ( 3.2.16 )along with the conditionA1/ = 0,A2= 0 andμ= 0, we obtain a further wave solution

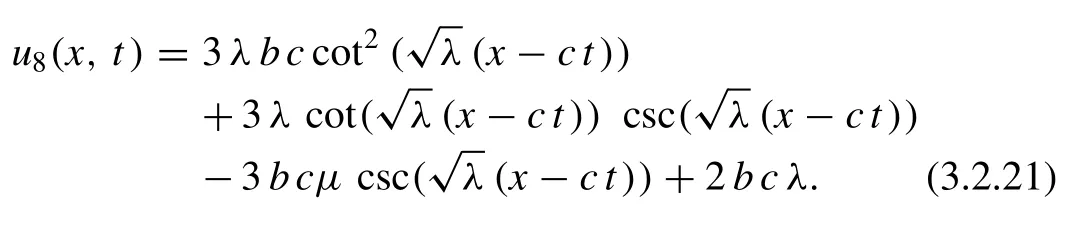
Case 3 :Whenλ= 0(Rational function solutions)

In this case, substituting the value ofu(ξ) into Eq.( 3.2.6 )along with ( 2.3 ) and ( 2.6 ) the left hand side of ( 3.2.6 ) turns out to be a polynomial inφandψ. Vanishing each coef fi cient of this polynomial equation yields a system of equations that is solved by Maple result the following values:

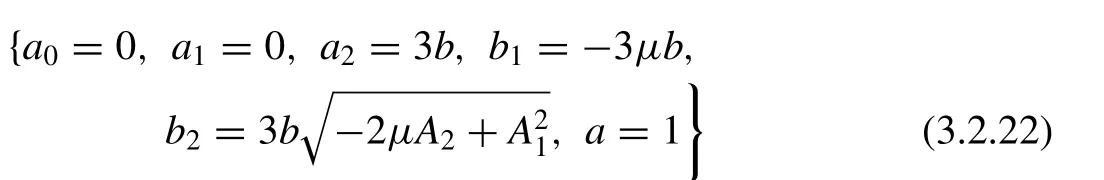
Inserting these values into ( 3.2.6 ) and using ( 2.2 ) and ( 2.6 ),we obtain the succeeding wave solution

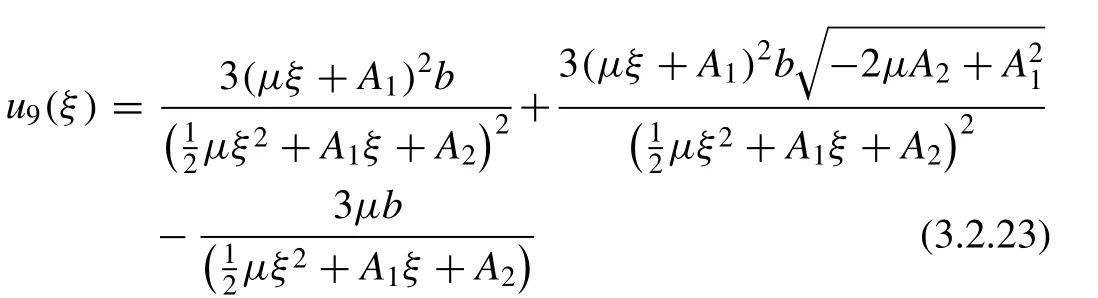
whereξ=x-ct.

4.Results and discussion

The (G′/G, 1/G)-expansion method has been delineated and executed to extract further general and new exact wave solutions to the Burger’s and the Benjamin–Bona–Mahony equations. The method is based on the direct treatment of the NLEEs with a certain substitution which leads to comparative easier ordinary differential equations. Additionally, it transforms a nonlinear equation to a simple algebraic equation. As the two parametersA1andA2are taken special values familiar type of solitary wave solutions are originated from the general solution. Whenμ= 0 in Eq. (2.1) , andbi= 0 in Eq. (2.9) ,the (G′/G, 1/G)expansion method turns into (G′/G)-expansion method. The key points of this method are that using the traveling wave variable the NLEEs transform into ODE. The ansatz presented here is that, the solution of this ODE is a polynomial in two variablesφ=(G′/G)andψ= 1/Gwhere,G=G(ξ)satis fi es a second order linear ordinary differential equationG′+λG=μ. Clearly, the solution of this ODE depends on values of different values onλ. Whenλis positive,we get the solution of this ODE in terms of hyperbolic functions and whenλis negative, the solution arises in terms of trigonometric functions and whenλis equal to zero, we get rational solutions.

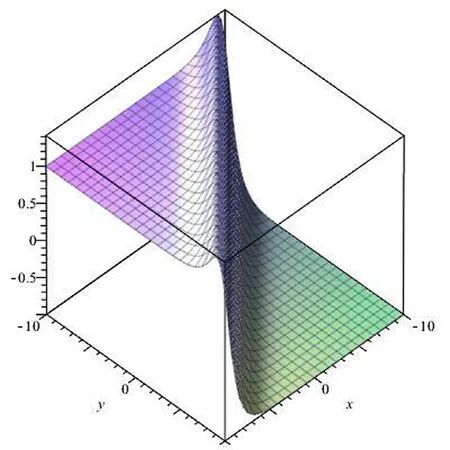
Fig. 1. Travelling wave solution of u1(x,t).

Exact solutions of the BBM [15-18] and Burger’s [19–21,58] equations are derived by many authors. Herein, all of our derived solutions are quite different (Appendix) that are in the form of combination of hyperbolic or trigonometric functions or in the form of rational functions. In case of some particular values of different parameters,some of our solutions match with the previous obtained solutions.

The traveling wave and behavior of the solutionsu1(x,t)of Eq. (3.1.9) andu2(x,t) of Eq. (3.1.10) are graphed in Figs. 1 and 2 , respectively for some fi xed values of the parametersλ= -1,c= 1 in the domain -10 ≤x,y≤ 10, -π/2 ≤x,y≤π/2 .

There are several methods existing to derive analytical solutions of NLEEs and each of them has some advantages and disadvantages. Some methods also provide solutions in a series form. It naturally raises a burning question to investigate the convergence of approximation of series. For instance, the Adomian decomposition method or the variational iteration [5] method depends on the initial conditions and some time there arise convergence issues. Some methods need linearization or to convert the inhomogenous boundary conditions to homogeneous and so on. In addition to, all numerical methods e.g. the fi nite difference or the fi nite element method must have initial and boundary conditions. The main advantages of (G′/G, 1/G)-expansion method over other methods are that it hits the problems in a straight forward fashion without using linearization, perturbation or any other restrictive assumption that may change the physical behavior of the model under discussion. It is worth to refer that the disadvantage of this method is: if the order of the reduced ODE is higher comparatively, it is mostly not possible to fi nd out a useful solution. In spite of this limitation, this method is useful for fi nding new exact solutions that are important in different fi eld contexts and to validate the numerical solutions.

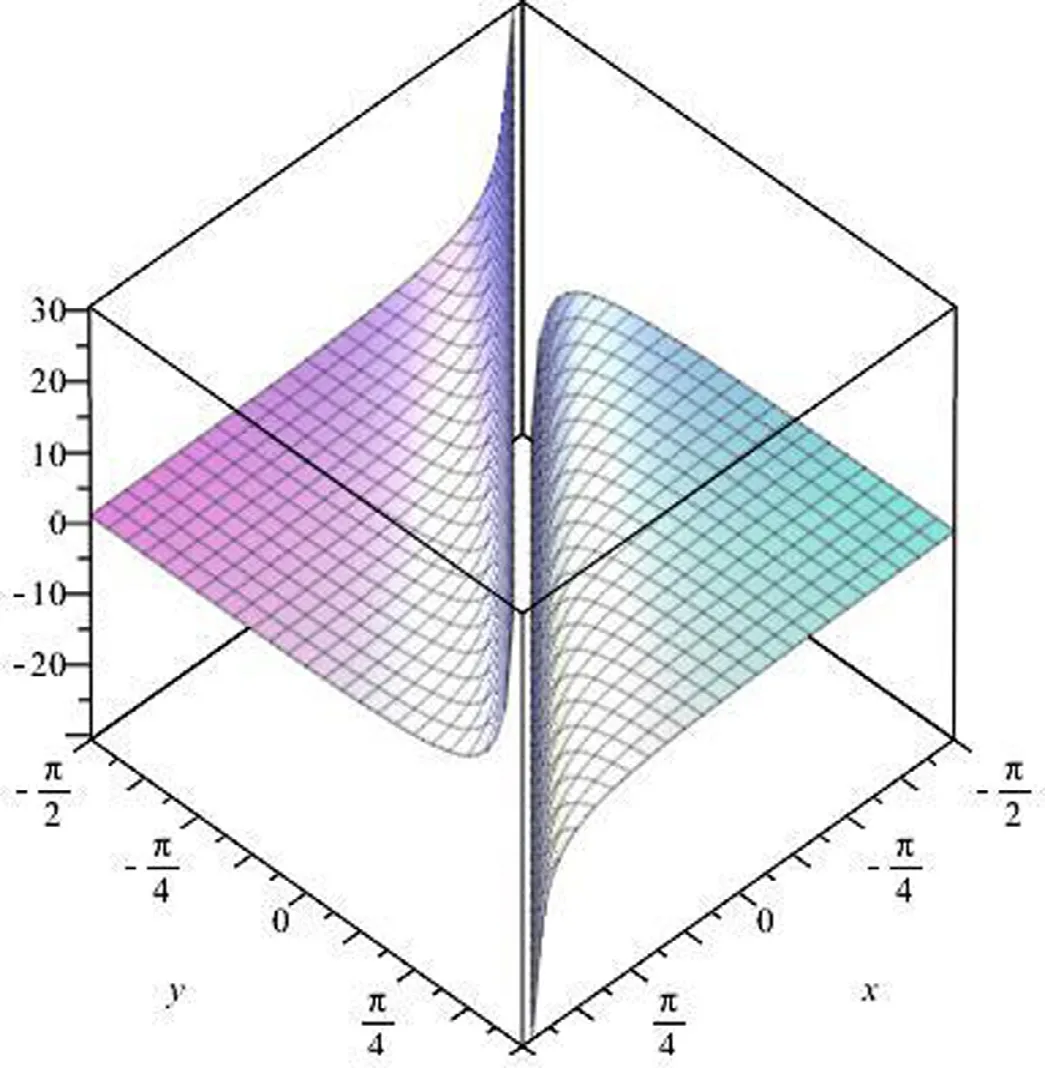
Fig. 2. Travelling wave solution of u2(x,t).

5.Conclusion

In this article, we introduced (G′/G, 1/G)-expansion method and used it to establish exact wave solutions to the nonlinear Burger’s and Benjamin–Bona–Mahony equations.Three types of traveling wave solutions in the form of hyperbolic, trigonometric and rational functions have been derived by this method. The derived analytical solutions have not previously been reported in the literature of exact travelling wave solution. The computational techniques of this method are simple and straightforward. This method can change the given dif fi cult problems into simple one and solve easily. Having been computerized method; it is powerful, reliable and effective. It is worthy of further study and might have substantial interest for applications in mathematical physics and engineering.

Funding

Acknowledgement

The authors would like to express their truthful thanks to the unidenti fi ed referees for their valuable comments and suggestions to improve the quality of this article. The authors also would like to convey their appreciation to Md. Nuruzzaman, Assistant Professor, English Discipline, Khulna University, Khulna, Bangladesh for his assistance in editing the English language.

Appendix

Wazwaz [58] investigated exact solutions of the BBM equation by two methods the sine-cosine method and the tanh-coth method. He derived the following four solutions by sine-cosine method.

By using tanh-coth method, Wazwaz also derived the following more other four different solutions

[1] W.X. Ma , W. Hongyou , H. Jingsong ,Phys. Lett. A 364 (1) (2007)29–32 .

[2] W.X. Ma , D.T. Zhou , Acta Math. Sci. 17 (1997) 168–174 .

[3] W.X. Ma , Y. You , Trans. Am. Math. Soc. 357 (5) (2004) 1753–1778 .

[4] S.T. Mohyud-Din , M.A. Noor , K.I. Noor , Int. J. Nonlinear Sci. Numer.Simul. 10 (2) (2011) 223–229 .

[5] S.T. Mohyud-Din , M.A. Noor , K.I. Noor , M.M. Hossaeini , Int. J. Nonlinear Sci. Numer. Simul. 11 (2) (2011) 87–92 .

[6] M.A. Noor , S.T. Mohyud-Din , A. Waheed , E.A. Al-Said , Appl. Math.Comput. 216 (2) (2010) 477–483 .

[7] M.A. Noor , S.T. Mohyud-Din , A. Waheed , Acta Appl. Math. 104 (2)(2008) 131–137 .

[8] S.T. Mohyud-Din , Y. Khan , N. Faraz , A. Yildirim , Int. J. Numer. Methods Heat Fluid Flow 22 (3) (2012) 335–341 .

[9] S.T. Mohyud-Din , M.A. Noor , A. Waheed , Zeitschrift für Naturforschung A 65 (2) (2014) 78–84 .

[10] M. Dehghan , J. Mana fi an , A. Saadatmandi , Int. J. Mod. Phys. B 25 (22)(2011) 2965–2981 .

[11] W.X. Ma , Phys. Lett. A 301 (1–2) (2002) 35–44 .

[12] W.X. Ma , K.I. Maruno , Phys. A Stat. Mech. Appl. 343 (1) (2004)219–237 .

[13] W.X. Ma , Y. You , Solitons Fractals 22 (2) (2004) 395–406 .

[14] W.X. Ma , B. Fuchssteiner , Int. J. Non-Linear Mech. 31 (3) (1996)329–338 .

[15] A.G. Johnpillai , A.H. Kara , A. Biswas , Appl. Math. Lett. 26 (3) (2013)376–381 .

[16] A. Biswas , Commun. Nonlinear Sci. Numer. Simul. 15 (10) (2010)2744–2746 .

[17] G.W. Wang , T.X. Xu , R. Abazari , Z. Jovanoski , A. Biswas , Acta Phys.Polonica A 126 (6) (2014) 1221–1225 .

[18] A. Biswas , S. Konar , Commun. Nonlinear Sci. Numer. Simul. 13 (4)(2008) 703–706 .

[19] G.W. Wang , T.Z. Zhou , A. Biswas , Roman. Rep. Phys. 66 (2) (2014)274–285 .

[20] A. Biswas , H. Triki , T. Hayat , O.M. Aldossary , Appl. Math. Comput.217 (24) (2011) 10289–10294 .

[21] A.J. Mohamad Jawad , M. Petkovi´c , A. Biswas , Appl. Math. Comput.216 (11) (2010) 3370–3377 .

[22] M. Mirzazadeh , M. Ekici , A. Sonomezoglu , S. Ortakaya , M. Eslami ,A. Biswas, Eur. Phys. J. Plus 131 (6) (2016) 166–177 .

[23] H.I. Abdel-Gawad , A. Biswas , Acta Phys. Polonica B 47 (4) (2016)1101–1112 .

[24] M. Mirzazadeh , M.E. Zerrad , D. Milovic , A. Biswas , in: Proceedings of the Romanian Academy, Series A, Vol. 17, 2016, pp. 215–221 .

[25] A. Biswas , E.V. Krishnan , P. Suarez , A.H. Kara , S. Kumar , Indian J.Phys. 87 (2) (2013) 169–175 .

[26] M. Antonova , A. Biswas , Commun Nonlinear Sci. Numer. Simul. 14(3) (2009) 734–748 .

[27] A.H. Bhrawy , K. Hasn Arak , A. Biswas , Acta Phys. Polonica A 125(5) (2014) 1099–1106 .

[28] A. Biswas , M.S. Ismail , Appl. Math. Comput. 216 (12) (2010)3662–3670 .

[29] A. Biswas , A.H. Kara , L. Moraru , H. Triki , S.P. Moshokoa , in: Proceedings of the Romanian Academy, Series A, Vol. 18, 2017, pp. 144–149 .

[30] T. Collins , A.H. Kara , A.H. Bhrawy , H. Triki , A. Biswas , Roman. Rep.Phys. 68 (3) (2016) 943–961 .

[31] A.H. Kara , A.H. Bhrawy , A. Biswas , Roman. J. Phys. 61 (3-4) (2016)367–377 .

[32] S.O. Adesanya , M. Eslami , M. Mirzazadeh , A. Biswas , Eur. Phys. J.Plus 130 (6) (2015) .

[33] P. Razborova , M. Luminita , A. Biswas , Roman. J. Phys. 59 (7–8) (2014)658–676 .

[34] D. Chao-Qing , W. Yue-Yue , A.Biswas ,Ocean Eng.81(2014)77–88 .

[35] S.T. Mohyud-Din , A. Yildirim , S. Sariaydin , Int. J. Numer. Methods Heat Fluid Flow 21 (3) (2011) 272–281 .

[36] S.T. Mohyud-Din , A. Yildirim , S. Sariaydin , S.A. Sezer , Int. J. Numer.Methods Heat Fluid Flow 21 (7) (2011) 822–827 .

[37] S.T. Mohyud-Din , E. Negahdary , M. Usman , Int. J. Numer. Methods Heat Fluid Flow 22 (5) (2012) 641–658 .

[38] M. Dehghan , M. Abbaszadeh , A. Mohebbi , Comput. Math. Appl. 68(3) (2014) 212–237 .

[39] M. Dehghan , M. Abbaszadeh , A. Mohebbi , J. Comput. Appl. Math. 286(2015) 211–231 .

[40] M. Sheikholeslami , D.D. Ganji , Chem. Phys. Lett. 667 (2017) 307–316 .

[41] M. Sheikholeslami , J. Mol. Liq. 234 (2017) 364–374 .

[42] M. Sheikholeslami , D.D. Ganji , Chem. Phys. Lett. 669 (2017) 202–210 .

[43] M. Sheikholeslami , D.D. Ganji , J. Mol. Liq. 229 (2017) 566–573 .

[44] M. Sheikholeslami , D.D. Ganji , J. Mol. Liq. 229 (2017) 530–540 .

[45] M. Sheikholeslami , M. Nimafar , D.D. Ganji , Alex. Eng. J. 56 (2) (2017)277–283 .

[46] M. Sheikholeslami , D.D. Ganji , J. Mol. Liq. 233 (2017) 499–507 .

[47] M. Sheikholeslami , D.D. Ganji , Mater. Des. 120 (2017) 382–393 .

[48] M. Sheikholeslami , S. Soleimani , D.D. Ganji , J. Mol. Liq. 213 (2016)153–161 .

[49] M. Sheikholeslami , D.D. Ganji , J. Mol. Liq. Part A, 224 (2016)526–537 .

[50] M. Sheikholeslami , M.T. Mustafa , D.D. Ganji , Particuology 26 (2016)108–113 .

[51] M. Sheikholeslami , D.D. Ganji , M.M. Rashidi , J. Magn. Magn. Mater.416 (2016) 164–173 .

[52] M. Sheikholeslami , D.D. Ganji , J. Taiwan Inst. Chem. Eng. 65 (2016)43–77 .

[53] M. Sheikholeslami , D.D. Ganji , Comput. Methods Appl. Mech. Eng.283 (2015) 651–663 .

[54] M. Sheikholeslami , M.M. Rashidi , D.D. Ganji , Comput. Methods Appl.Mech. Eng. 294 (2015) 299–312 .

[55] M. Sheikholeslami , M.M. Rashidi , D.D. Ganji , J. Mol. Liq. 212 (2015)117–126 .

[56] M. Sheikholeslami , D.D. Ganji , M.M. Rashidi , J. Taiwan Inst. Chem.Eng. 47 (2015) 6–17 .

[57] M. Hatami , M. Sheikholeslami , D.D. Ganji , Powder Technol. 253 (2014)769–779 .

[58] A.M. Wazwaz , Partial Differential Equations and Solitary Waves Theory, Springer, New York, 2009 .

[59] M.L. Wang , X.Z. Li , J.L. Zhang , Phys. Lett. A 372 (2008) 417–423 .

[60] X.L. Li , Q.E. Li , L.M. Wang , Appl. Math. J. Chin. Univ. 25 (2010)454–462 .