基于Grümwald-letnikov的分数阶积分图像去噪算法

陈 莉

(陕西理工大学 物理与电信工程学院， 陕西 汉中 723000)

分数阶积分理论诞生于300年前，在近年，随着对其在信号分析处理领域的应用研究，发现分数阶积分在衰减信号高频信息的同时能够保留低、中频信息，因此可以被应用于图像去噪，这一新的方法在近年成为研究热点。

图像去噪是图像处理的重要步骤，经典图像去噪算法包括中值滤波去噪算法、均值滤波去噪算法、维纳滤波去噪算法等基于滤波的去噪算法[1-3]。这些算法在去噪的同时图像纹理细节信息丢失较多，造成图像模糊，因此研究人员又提出了基于滤波的改进算法[4-6]，其主要目标是在去噪的同时尽可能保留图像纹理细节信息。信号分数阶积分的频率特性是高频成分被衰减的同时，甚高频成分可以被非线性地保留，因此应用分数阶积分去噪可以较好地保留图像纹理细节信息。分数阶积分图像去噪算法的本质是对图像像素进行积分运算，其方法是构造积分模板，用模板与图像进行卷积运算，实现图像像素的积分，从而实现图像去噪。

1 分数阶积分定义及频率特性分析

1.1 Grümwald-letnikov定义

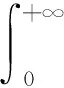
Grümwald-letnikov是分数阶微积分的数学定义，分阶数为正表示分数阶微分运算，分阶数为负表示积分运算。分数阶积分的Grümwald-letnikov定义[7]为

(1)

1.2 信号分数阶积分的频率特性分析[8-9]

已知信号f(t)的傅里叶变换为

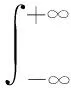
(2)

根据傅里叶变换的积分性质得到

其中v的取值小于0，得到信号的傅里叶变换：

(3)

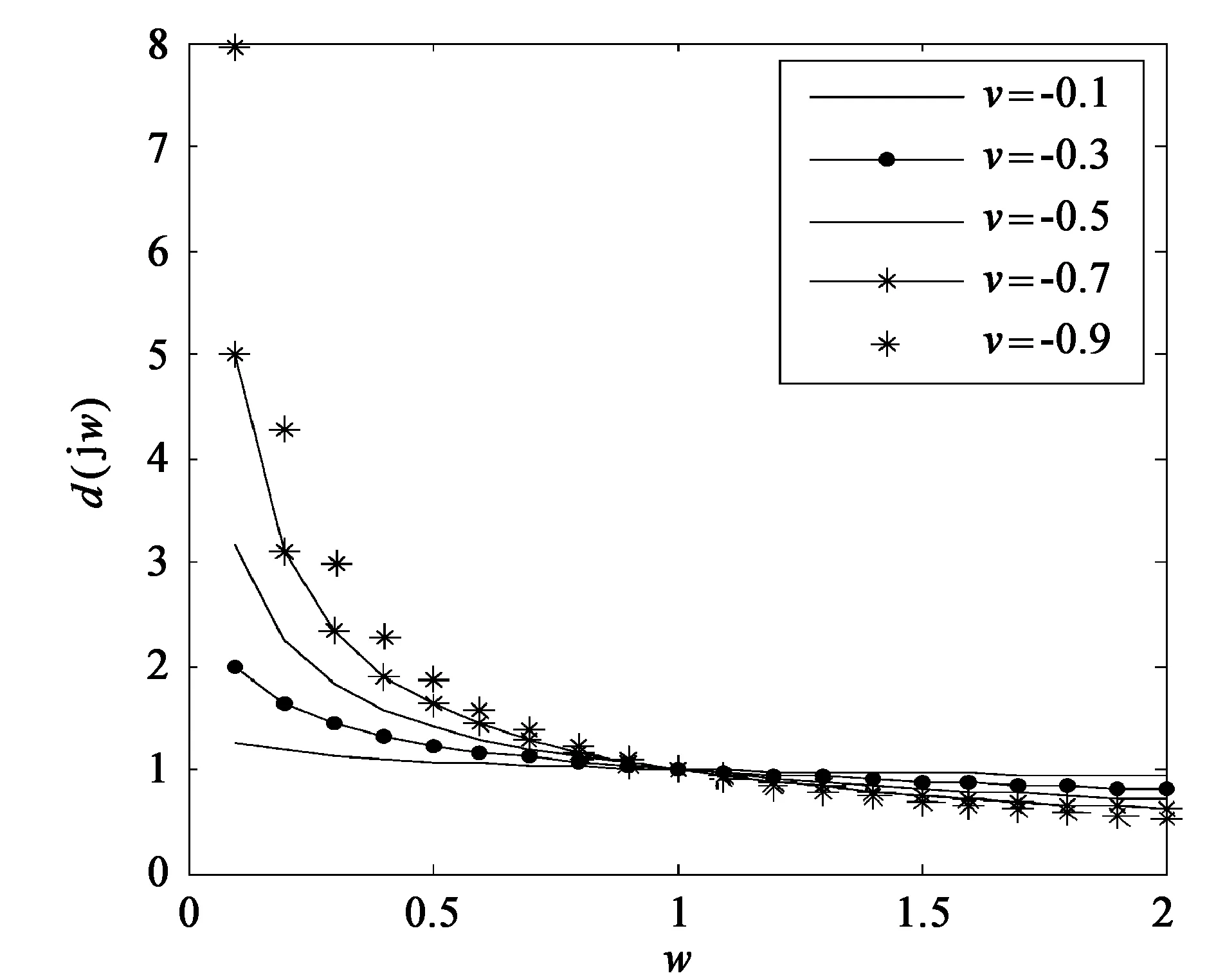
图1 分数阶积分运算的 信号频率特性曲线

分数阶积分可以看成是广义的调幅调相，振幅随频率成分数阶幂指数变换，相位是频率的广义Hilbert变换。振幅特性是偶函数，相位特性是奇函数。

如图1所示，当-11频率段，分数阶积分对高频信号具有一定的衰减作用，分数阶积分的分阶数的绝对值增大时，高频信号的衰减程度有所增大，说明分数阶积分运算可以衰减高频信号，实现图像去噪；但随着信号频率的增大，频率特性曲线平稳，说明甚高频成分可以被非线性保留，因此在应用分数阶积分进行图像去噪的同时可以非线性保留图像边缘细节信息。

2 分数阶积分去噪算法构造

分数阶积分去噪的本质是对图像像素进行积分运算，分数阶积分去噪算法的构造本质是从分数阶积分数学定义出发，提取用于构造积分去噪模板的系数，将系数放入模板后，使用模板与待处理的含噪图像卷积，通过卷积运算，实现图像去噪。

算法实现步骤如下：(1)推导模板系数；(2)构造去噪模板；(3)模板与待去噪图像卷积运算。

2.1 模板系数推导

根据分数阶微积分Grümwald-letnikov定义，分阶数v为负时，公式(1)数学表达式为积分运算，展开得到：

水平方向积分运算数学表达式为

(4)

垂直方向积分运算数学表达式为

(5)

对角方向积分运算数学表达式为

(6)

从公式(4)—(6)得到模板系数：

(7)

2.2 去噪模板构造

根据2.1节数学推导得到的模板系数，构造积分去噪滤波器模板。如图2所示，为了达到较好的去噪效果，本文将得到的模板系数应用到滤波器模板的水平正方向、水平负方向、垂直正方向、垂直负方向及45°、135°、225°、275°对角方向，得到八方向的滤波模板，可以实现对含噪图像8个方向的去噪处理。

(-v)(-v+1)/20(-v)(-v+1)/20(-v)(-v+1)/20-v-v-v0(-v)(-v+1)/2-v8-v(-v)(-v+1)/20-v-v-v0(-v)(-v+1)/20(-v)(-v+1)/20(-v)(-v+1)/2

图2 分数阶积分去噪模板

2.3 图像去噪的卷积运算

用设计的分数阶积分去噪模板与图像进行卷积运算，可以实现对图像的去噪处理[10]。卷积运算如式(8)：

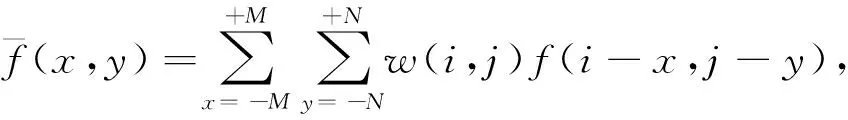
(8)

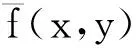
3 算法去噪效果分析

3.1 加性高斯白噪声下去噪效果

使用分数阶积分算法处理含有加性高斯白噪声的plane.bmp图像，分阶数v取值为-0.1、-0.3、-0.5、-0.7、-0.8、-0.9，处理效果如图3所示。

图3 高斯噪声下分数阶积分算法去噪效果图

图3所示的实验结果可以表明：分数阶积分算法可以实现对图像的去噪，在去噪的同时保留图像纹理信息；并且随着分阶数绝对值的增大，算法的去噪效果逐步提高，v=-0.9时，图像去噪效果最好。

3.2 乘性噪声下去噪效果

使用分数阶积分算法处理含有乘性噪声的qianbi.jpg图像，分阶数v取值为-0.2、-0.4、-0.6、-0.9，处理效果如图4所示。

图4 乘性噪声下分数阶积分算法去噪效果图

图4所示实验结果表明：分数阶积分算法在去噪时，很好的保留了图像边缘信息，图像没有因为去噪而变得模糊。随着分阶数绝对值的增大，图像的去噪效果逐步提高，说明算法的去噪能力随着分阶数绝对值的增大而提高。

3.3 分数阶积分去噪算法与经典去噪算法效果对比

3.3.1 加性高斯噪声下效果对比

对含有加性高斯白噪声的hudie.jpg图像，分别使用分数阶积分去噪算法、经典中值滤波算法和维纳滤波算法处理，分数阶积分算法的分阶数v取值为-0.6，处理效果如图5所示。

图5 加性高斯白噪声下分数阶积分算法与经典去噪算法效果对比

图5所示的实验结果表明：分数阶积分去噪算法在高斯噪声下的去噪效果与中值滤波算法及维纳滤波算法相比，有明显优势。分数阶积分算法滤除了大部分噪声，并且较好地保留了图像的纹理细节信息，图像在去噪处理后较清晰。中值滤波算法具备一定的去噪能力，但去噪处理后的图像仍含有大量噪声。维纳滤波的去噪效果优于中值滤波，但在经过去噪处理后图像中依然含有少量噪声，且图像的纹理信息存在丢失现象，边缘变得模糊。

3.3.2 乘性噪声下对比

对含有乘性噪声的katong.jpg图像，分别使用分数阶积分去噪算法、经典中值滤波算法和维纳滤波算法处理，分数阶积分算法的分阶数v为取值为-0.6，处理效果如图6所示。

图6 乘性噪声下分数阶积分去噪算法与经典算法去噪效果对比

图6所示的实验结果表明：分数阶积分去噪算法在乘性噪声下的去噪效果与中值滤波算法及维纳滤波算法相比，有明显优势；维纳滤波的去噪效果优于中值滤波。分数阶积分去噪算法不仅滤除了大部分噪声，并且图像边缘纹理信息保留较好，去噪处理后的图像较清晰，没有因为去噪丢失大量细节边缘纹理信息。

4 结束语

分数阶积分在图像去噪方面的应用具有简单性和高效性，可以在去噪的同时较好地保留图像纹理信息，使得含噪图像在去噪处理后边缘纹理较清晰，图像不模糊。

本文从频率特性角度出发，分析了分数阶积分应用于图像去噪的可行性，从分数阶积分数学模型出发，构造了八方向的分数阶积分模板，即在4个水平、垂直方向的基础上增加了4个对角方向的模板系数，用这样的多方向模板与含噪图像卷积运算，可以扩大图像去噪处理范围，更有效、更全面地去除图像噪声。但在使用分数阶积分算法去噪时，分阶数的取值没有唯一确定，如果能针对不同纹理特点的图像，自适应确定最佳分阶数，将大大提高算法性能，这将是进一步研究的方向。

[参考文献]

[1] 郭海霞,解凯.一种改进的自适应中值滤波算法[J].中国图象图形学报,2007,12(7):1185-1188.

[2] 李宁.基于方向信息的图像去噪算法研究[D].西安:西安电子科技大学,2007.

[3] 陈乃金,周鸣争,潘冬冬.一种新的维纳滤波图像去高斯噪声算法[J].计算机系统应用,2010,19(3):111-114.

[4] 张丽果.快速非局部均值滤波图像去噪[J].信号处理,2013,29(8):1043-1048.

[5] 刘孝艳.变分、PDE和非局部滤波在图像去噪中的应用研究[D].西安:西安电子科技大学,2015.

[6] 罗亮.基于MCMC采样的非局部图像去噪方法研究[D].西安:西安电子科技大学,2015.

[7] 黄果,蒲亦菲,陈庆利,等.基于分数阶积分的图像去噪[J].系统工程与电子技术,2011,33(4):925-936.

[8] 张富平,周尚波,赵灿.基于分数阶偏微分方程的彩色图像去噪新方法[J].计算机应用研究,2013,30(3):946-949.

[9] 杨柱中,周激流,郎方年.基于分数阶微积分的噪声检测和图像去噪[J].中国图象图形学报,2014,19(10):1418-1429.

[10] 杨农丰,吴成茂,屈汉章.基于偏微分方程的混合噪声去噪研究[J].计算机应用研究,2013,30(6):1899-1902.