关于马氏距离模糊聚类的有效性指标研究
祖志文, 李 秦
(兰州交通大学 数理学院, 甘肃 兰州 730070)
聚类有效性是指通过聚类算法得到数据集的聚类结构后,对聚类结果做合理性和有效性的评价。对于模糊聚类而言,模糊聚类算法在对样本集进行聚类分析前需要事先给定聚类数目,合理聚类数目的确定需由有效性函数来完成,因此模糊聚类有效性问题可转化为最佳聚类数的决策问题。
历史上对模糊聚类有效性指标已早有研究,如划分系数、划分熵,及改进的基于可能性分布的聚类有效性函数FP(U;c)、FS有效性指标[1]、Kwon指标[2]、Kim指标[3]、PBMF模糊有效性指标[4]。近几年,对于模糊聚类的有效性指标的研究层出不穷,基于数据集的几何结构设计的模糊聚类有效性指标表现较佳,如很多学者对紧致性和分离性度量公式分别加以改进,从而利用两者之比构造出新的有效性指标[5-6];Sreeram Joopudi等人[7]提出了分级距离指标GD-index;Chatti Subbalakshmi等人[8]将轮廓函数与模糊聚类结合,可以寻找动态数据集的最佳聚类数。
以上为基于欧氏距离的经典模糊聚类FCM算法研究的模糊聚类有效性指标,对基于马氏距离的模糊聚类算法并不适用。本文首先通过列举基于欧氏距离的模糊聚类有效性指标分析不同类型有效性指标的准确性,然后给出基于马氏距离的模糊聚类算法M-FCM,根据M-FCM与FCM算法的差异提出一种适用于M-FCM算法的有效性指标,最后结合算法在真实数据集上进行实验,以验证所提出的有效性指标的准确性。
1 两种模糊聚类有效性指标对比
1.1 基于数据集模糊划分
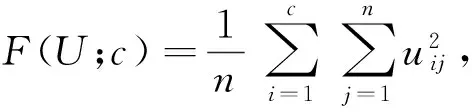
FP(U;c)=F(U;c)-P(U;c),
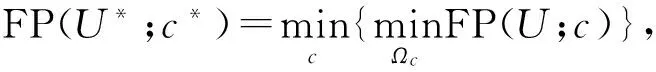
Kim指标是通过计算所有重叠度的均值来衡量聚类的有效性,重叠度是聚类对交叠部分相关度的权值之和。指标如下所示:

1.2 基于数据集几何结构
FS有效性指标定义如下:
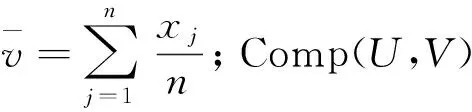
针对Kim指标的缺点提出的有效性指标SC定义如下:
SC=ω×Sepn(c,U)+(1-ω)×Comn(c,U),
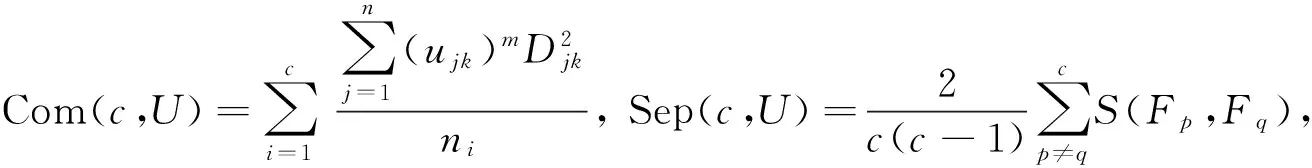
1.3 两种有效性指标对比分析
为比较基于数据集模糊划分与几何结构的模糊聚类有效性指标,选择可适用于马氏距离的模糊聚类算法有效性指标的研究方向,使得算法能准确识别最佳聚类数目,下面将常用的两个基于数据集模糊划分的模糊聚类有效性指标FP(U;c)、Kim与两个基于数据集几何结构的模糊聚类有效性指标FS、SC分别用于经典的模糊聚类算法FCM,在5个来自UCI数据库的真实数据集Iris、Pima、Breast Cancer、Wine、WDBC上进行实验。Iris数据集由150个样本组成,并且每个样本有4个属性,分为3个类别,第一类与其它两类完全分离,而第二类与第三类之间有交叉。Pima数据集有768个样本,由两个相互交叠的类组成,每个样本有8个属性。Breast Cancer数据集由9维空间的683个样本组成,分为两个交叠的子类。Wine数据是由13维空间的178个样本组成,共分为3个种类,3类之间完全分离。WDBC数据集由30维空间的569个样本组成,分为两类。不同类型有效性指标对上述5个真实数据集所获聚类数及相应的有效性值如表1所示。
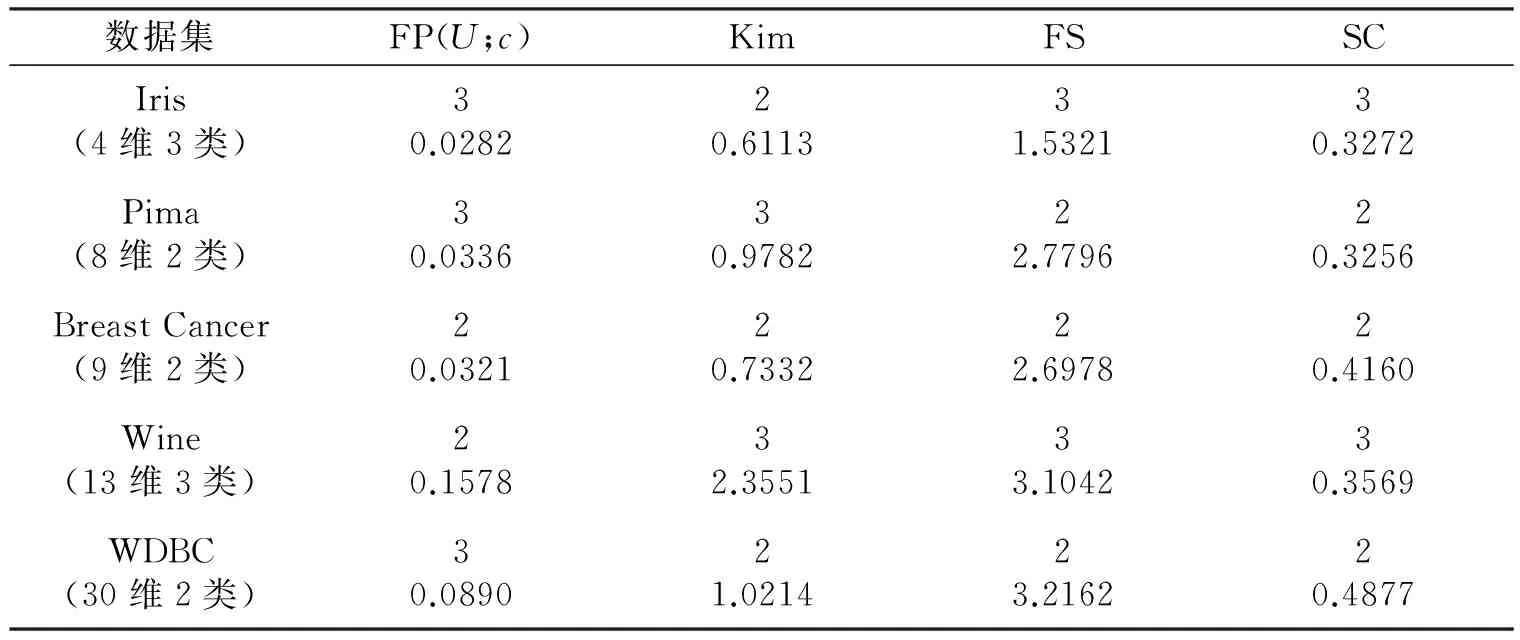
表1 有效性指标对比
从表中可以看出,FP(U;c) 指标处理多维数据的能力欠佳,对较高维的Pima、Wine和WDBC数据集失效;Kim指标会随着聚类数的增加而呈现单调递增的趋势,而且当对包含交叠子集的数据集Iris、Pima进行聚类时,该指标不能够准确的识别聚类数。而有效性指标FS、SC在这5个真实数据聚类实验中,虽然收敛速度明显不如两个基于数据集模糊划分的模糊聚类有效性指标,但都可得到符合实际的最佳聚类数,说明基于数据集几何结构研究的模糊聚类有效性指标性能较佳。
2 基于马氏距离模糊聚类的有效性
2.1 基于马氏距离的模糊聚类算法
经典的FCM算法是只适合于球形数据,而用于非球形或椭球形结构的许多算法,都在处理高维数据时效果很差,将经典的FCM聚类中的欧氏距离用马氏距离代替,可以消除量纲不同对聚类分析的影响,排除变量之间相关性的干扰,这种基于马氏距离的模糊聚类算法也多用来处理复杂的多维数据[10]。
FCM算法的优化目标函数为
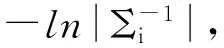
最小化J,对ci,uij,Σi求偏导,并令它们等于零,得
(1)
(2)
(3)
M-FCM算法描述如下:
初始化:给定聚类类别数c,2≤c≤n,n是数据个数,设定迭代阈值ε,初始化聚类中心矩阵C(0),设置迭代计数器L=0。
步骤一:用(1)式计算或更新隶属度矩阵U(L)。
步骤二:用(2)式更新聚类中心矩阵C(L+1)。
步骤三:如果‖C(L)-C(L+1)‖<ε,则算法停止并输出隶属度矩阵U和聚类中心C,否则令L=L+1,转向步骤一。其中,‖·‖为某种合适的矩阵范数。
2.2 基于马氏距离的模糊聚类有效性指标
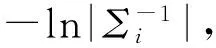
(1)用目标函数的均值来衡量类内紧致度:
(k=1,2,…,c;j=1,2,…,n)
其中,Σi(3)式计算。当compact(U,C,Σi)越小时,类内样本越紧致,当compact(U,C,Σi)取得最小值时,则类内紧致程度最好,相似度最高。
(2)用类间聚类中心的总距离来定义类间分离度:
其中Dik为聚类中心的距离,当separate(C)取得最大值时,类间分离程度最好。
(3)用各个类内最大模糊隶属度值的均值来衡量类间清晰度:
清晰度用来度量模糊聚类划分结果是否分明,其值越小,则表明划分越清晰。
基于上述的紧致度、分离度和清晰度,提出了一种基于马氏距离的模糊聚类有效性指标CSD:
其中权重因子α和1-α用来补偿紧致度和分离度的度量差别,使得在不同数据空间中紧致度和分离度取值变化范围较大的一方赋予较小的权重,聚类结果更清晰。一般情况下,紧致度权重α略大于分离度权重1-α,这里取α=0.6,1-α=0.4。由上述可知,CSD指标的值越小,说明样本集的类内紧致程度越高、类间分离程度越大、类间清晰程度越明显,即CSD指标的最小值对应的聚类数目c为最佳聚类数目。
3 实验结果与分析
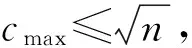
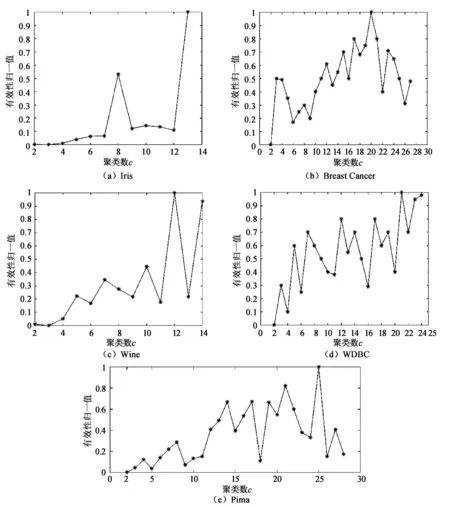
图1 CSD有效性指标平均值随聚类数目c的变化图
对于5种数据集Iris(n=150,c=3)、Breast Cancer(n=683,c=2)、Wine(n=178,c=3)、WDBC(n=569,c=2)、Pima(n=768,c=2)的聚类算法运行结果如表2所示。
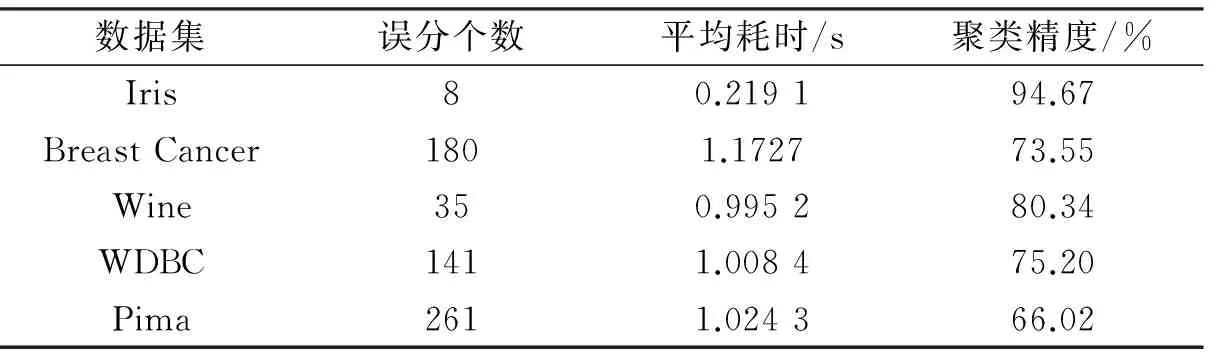
表2 聚类算法运行结果
实验结果分析:由图1(a)—(e)可知,CSD有效性指标对Iris数据集在聚类数c=3时达到极小值,对Breast Cancer数据集在聚类数c=2时达到极小值,对Wine数据集在聚类数c=3时达到极小值,对WDBC数据集在聚类数c=2时达到极小值,对Pima数据集在聚类数c=2时达到极小值,即新的有效性指标对5个标准数据集都可以正确地确定数据集的最佳聚类数。由表2可知,基于马氏距离的模糊聚类算法在CSD有效性指标检验下可以有效聚类,并且算法的运行时间和聚类精度都在合理范围内。通过实验,可以说明本文提出的有效性指标保证了基于马氏距离的模糊聚类算法M-FCM在多维数据中聚类时可以准确识别最佳聚类数目。
4 结束语
本文通过对比分析基于数据集模糊划分与几何结构的模糊聚类有效性指标,确定了类内紧致度、类间分离度与类间清晰度结合的有效性研究方向,针对基于马氏距离的模糊聚类算法提出新的度量标准,构造出基于马氏距离的模糊聚类有效性指标CSD。最后结合算法在真实数据集上进行实验,验证了该有效性指标适用于基于马氏距离的模糊聚类算法,保证了算法在多维数据上聚类的有效性。
[参考文献]
[1] 李春生.模糊聚类的组合方法及其应用研究[D].长沙:湖南大学,2010.
[2] KWON S H.Cluster validity index for fuzzy clustering[J].Electronics Letters,1998,34(22):2176-2177.
[3] KIM D W,Lee K H,Lee D.On cluster validity index for estimation of the optimal number of fuzzy clusters[J].Pattern Recognition, 2004,37(10):2009-2025.
[4] PAKHIRA M K,BANDYOPADHYAY S,MAULIK U.A study of some fuzzy cluster validity indices, genetic clustering and application to pixel classification[J].Fuzzy Sets and Systems,2005,155(2):191-214.
[5] 孔攀,邓辉文,黄艳艳,等.一个新的模糊聚类有效性指标[J].计算机工程,2009,35(12):143-144.
[6] 汤官宝.一种新的模糊聚类有效性指标[J].计算机与现代化,2014(7):16-18.
[7] SREERAM J,SURAJ S R,NARASIMHAN S,et al.A New Cluster Validity Index for Fuzzy Clustering[J].IFAC Proceedings Volumes,2013,46(32):325-330.
[8] CHATTI S,RAMA K G,KRISHNA M R S,et al.A Method to Find Optimum Number of Clusters Based on Fuzzy Silhouette on Dynamic Data Set[J].Procedia Computer Science,2015,46:346-353.
[9] 张妨妨.模糊聚类技术的研究及应用[D].无锡:江南大学,2013.
[10] 蔡静颖.模糊聚类算法及应用[M].北京:冶金工业出版社,2015:20-100.

