Q345D钢的热变形抗力研究

李海阳 纪登鹏 周晓航 张 梅

(省部共建高品质特殊钢冶金与制备国家重点实验室、上海市钢铁冶金新技术开发应用重点实验室和上海大学材料科学与工程学院，上海 200072)

Q345D钢是一种低合金高强度工程结构钢，具有良好的塑性、韧性、耐低温性能、加工工艺性能和焊接性能等，被广泛应用于石油、车辆、船舶、建筑和压力容器等领域[1- 4]。在Q345D钢的塑性加工过程中，其变形抗力是确定塑性加工参数的重要基础，也是Q345D钢的主要力学性能指标。因此，建立Q345D钢的变形抗力模型可为Q345D钢塑性加工控制过程提供理论基础，从而优化生产工艺，提高产品质量。本研究利用Gleeble- 3500热- 力模拟试验机，对Q345D钢进行高温单道次压缩试验，分析Q345D钢塑性加工的变形参数即变形温度、变形速率和变形程度对Q345D钢变形抗力的影响，建立Q345D钢的塑性变形抗力模型。

1 试验材料及方法

试验材料取自尺寸600 mm×600 mm的Q345D钢样坯，加工成φ10 mm×15 mm的圆柱体试样，其化学成分如表1所示。

表1 试样的化学成分(质量分数)Table 1 Chemical composition of the samples (mass fraction) %

采用Gleeble- 3500热模拟试验机进行单道次压缩试验。采取抽真空保护试样，以免试样在高温下氧化。试样以10 ℃/s的速度加热到1 250 ℃，保温5 min，以保证奥氏体均匀化，然后以5 ℃/s的速度冷却到变形温度，保温60 s后进行压缩试验。变形结束后立即水淬。变形量为50.34%，即应变量为0.7；变形温度：1 200、1 150、1 100、1 050、1 000、950、900、850、800、750 ℃；变形速率：0.01、0.1、1、10 s-1。单道次压缩试验工艺见图1。

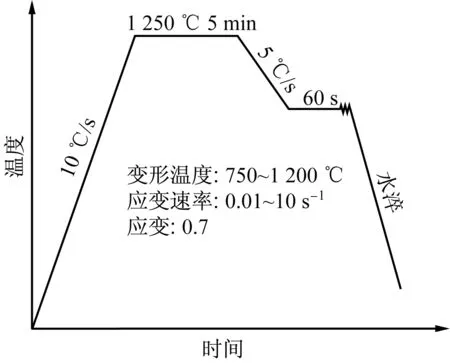
图1 单道次压缩试验工艺图Fig.1 Schematic illustration of single pass compression test

2 试验结果与分析

2.1 真应力- 真应变曲线

图2(a)为Q345D钢在应变速率为0.1 s- 1、不同变形温度下的真应力- 真应变曲线，图2(b)为Q345D钢在1 000 ℃变形温度、不同应变速率下的真应力- 真应变曲线。由图2可以看出，在一定的应变速率下，随着变形温度的升高，变形抗力逐渐减小，真应力- 真应变曲线由加工硬化型向动态再结晶型转变；在一定变形温度下，随着应变速率的升高，变形抗力逐渐增大，真应力- 真应变曲线由动态再结晶型向加工硬化型转变。由Q345D钢的真应力- 真应变曲线可知，降低变形温度和提高应变速率，均可增大试验钢的变形抗力，且只有在较低的变形速率和较高的变形温度下，Q345D钢才易发生动态再结晶。

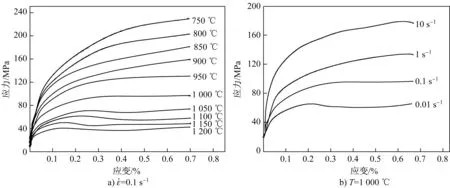
图2 Q345D钢的真应力- 真应变曲线Fig.2 True stress- true strain curves for Q345D steel

2.2 变形温度对变形抗力的影响

图3所示为Q345D钢在一定变形程度(ε=0.3、0.6)、不同变形速率下，变形抗力与变形温度之间的关系。从图3可以看出，在相同变形速率下，lnσ随着变形温度的升高呈直线降低的趋势，即lnσ=aT+b。因此，变形抗力σ随变形温度T的升高呈指数降低关系，变形温度T对变形抗力σ的影响系数KT可用式(1)表示：

(1)

式中：σ为变形抗力，MPa；σ0为基准变形抗力，MPa；

图3 Q345D钢在不同应变量和应变速率下变形抗力和变形温度的关系Fig.3 Relationship between deformation resistance and temperature of 345D steel under different strain rates and deformation degrees

T为变形温度，℃；A、B为与材料相关的系数。

2.3 变形速率对变形抗力的影响

(2)

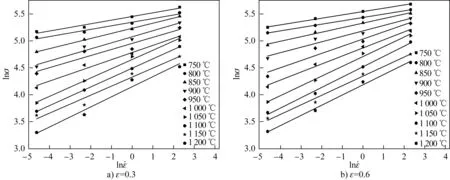
图4 Q345D钢在不同应变量和变形温度下变形抗力和应变速率的关系Fig.4 Relationship between deformation resistance and strain rate of Q345D steel under different temperatures and deformation degrees

2.4 变形程度对变形抗力的影响

变形程度对变形抗力的影响即应力与应变的关系。由图2(a)可得：在低应变速率、高变形温度，即发生动态再结晶条件下，变形抗力首先随着变形程度的增加而快速增大，出现峰值后，变形程度继续增加，变形抗力则逐渐减小，最后趋于稳定；而在高应变速率、低变形温度，即发生动态硬化条件下，变形抗力则随着变形程度的增加而不断增大；变形抗力的增加速率与变形程度的大小成反比。由此可见，变形程度对变形抗力的影响较复杂，变形程度ε对变形抗力σ的影响系数可用式(3)表示[5]：

(3)

式中：σ0为应变量为ε0时的基准变形抗力，MPa；ε、ε0分别为应变量和基准应变量；D、E为与材料相关的系数。

3 变形抗力模型的建立与分析

3.1 变形抗力模型

对于具体钢种而言，变形抗力主要受变形温度、变形速率和变形程度的影响。因此，变形抗力可以表示成关于温度、变形程度和变形速率的函数。目前有多种变形抗力模型[6- 10]，其中周纪华、管克智提出的变形抗力模型[6- 7]公式(4)，综合考虑了变形温度、变形速率和变形程度对变形抗力的影响，具有广泛的适用性，因此得到了广泛的应用。

(4)

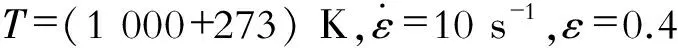
根据以上Q345D钢的变形条件对变形抗力的影响分析，可以看出变形条件对变形抗力的影响与周纪华等的模型相符。因此采用模型公式(4)对Q345D钢的变形抗力进行拟合比较合理。根据最小二乘法计算方法，采用Origin软件对试验所得的40条真应力- 真应变曲线数据进行非线性综合回归，得相关系数a1～a6，如表2所示。

表2 回归系数Table 2 Regression coefficients

将回归系数代入模型(4)中，可得Q345D钢的变形抗力拟合式(5)：

(5)

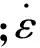
3.2 回归曲线与实测曲线的比较

跟据式(5)获得不同工艺参数(变形温度、应变速率和变形程度)下变形抗力的拟合值，将其与压缩试验所得的变形抗力值进行对比，结果如图5所示。从图5可以看出，利用变形抗力模型式(5)计算获得的拟合值与实测值之间的偏差较小。

图5 变形抗力的试验值与拟合值比较Fig.5 Comparison of the fitted and the experimented deformation resistances

为更好地说明模型的拟合程度，将真应力- 真应变曲线的模拟值与实测值进行比较，如图6所示。从图6中也可以看出，模型计算值与实测值吻合较好。

由于实验设备以及试样尺寸等因素的影响，使得试验数据与真实数据存在一定误差。因此，拟合曲线和试验数据会有一定误差。如在变形温度为750和950 ℃、应变速率为0.1 s-1时，误差较大，但最大误差值不超过25 MPa；其余曲线也有误差，但误差值较小。

4 结论

(1)以试验得到的真应力- 真应变曲线为基础，分析了变形温度、变形速率和变形程度对Q345D钢变形抗力的影响。在应变速率和变形程度一定时，变形抗力随着变形温度的升高而减小；在变形温度和变形程度一定时，变形抗力随着应变速率的增加而增大；而在变形温度和应变速率一定时，变形程度对变形抗力的影响较为复杂。在高变形温度和低应变速率下， 变形抗力随着变形程度的增加而增大，但达到峰值后由于发生了动态再结晶，变形抗力开始下降，并达到相对稳定状态；在低变形温度和高应变速率下，变形抗力则随着变形程度的增加不断增大。

图6 不同应变速率下真应力- 真应变曲线的回归计算结果与试验结果比较Fig.6 Comparison of the experimental data and regression calculation value of flow stresses at different stain rates

(2)综合考虑了变形温度、变形速率以及变形程度对变形抗力的影响，并利用周- 管数学模型，对试验数据进行非线性回归，得出Q345D钢的变形抗力数学模型，将拟合数据与试验数据进行对比，得出该模型的拟合度较好，可投入实际应用。

[1] 周许, 王立新, 胡建成, 等. 提高低合金高强度钢Q345D低温冲击功的工艺研究[J]. 大型铸锻件, 2011(1): 22- 25.

[2] 毛颖, 余驰斌, 叶传龙, 等. Q345D静态再结晶行为的分析[J]. 热加工工艺, 2015, 44(2): 36- 40.

[3] 杨克, 杨可, 包晔峰. Q345D钢埋弧焊接头组织与性能[J]. 电焊机, 2014, 44(1): 87- 90.

[5] 赵峻, 朱俊峰, 隋凤利, 等. 一种高锰奥氏体无磁钢变形抗力模型的建立与验证[J]. 安徽工业大学学报(自然科学版), 2015,32(1): 7- 11.

[6] 周纪华, 管克智. 金属塑性变形阻力[M]. 北京：机械工业出版社, 1989.

[7] 李鸿友, 周铖, 贺莹莹,等. 30MnSi钢热变形抗力的数学模型[J]. 上海金属, 2014, 36(2):59- 62.

[8] 宋仁伯, 项建英, 刘良元, 等. 316L不锈钢的热变形抗力模型[J]. 机械工程材料, 2010, 34(6)：85- 88.

[9] LIN Y C, LI K K, LI H B, et al. New constitutive model for high- temperature deformation behavior of inconel 718 superalloy[J]. Materials & Design, 2015, 74:108- 118.

[10] 许勇顺, 柳建韬, 聂明, 等. 金属热变形应力- 应变曲线数学模型的研究与应用[J]. 应用科学学报, 1997, 15(4): 379- 384.