基于改进卡尔曼滤波的陀螺仪误差补偿算法*
李鲁明,赵鲁阳,唐晓红,3,何 为*,李凤荣
(1.中国科学院上海微系统与信息技术研究所宽带无线技术实验室,上海 200050;2.中国科学院大学,北京 100049;3.上海师范大学信息与机电工程学院,上海 200234)
导航系统通常采用卫星导航系统进行定位如北斗导航、GPS导航等,但在卫星信号受遮挡时,如车辆行驶在隧道、峡谷、高楼等区域,无法接收4颗及以上卫星信号进行定位时,通常选择采用惯性导航进行定位解算。惯性导航使用加速度计、陀螺仪等惯性器件对载体的姿态进行求解,从而解算得出载体的速度、位置等导航定位信息。
随着MEMS技术的不断发展,MEMS加速度计和陀螺仪等惯性器件在惯性导航中的应用越来越广泛[1],但是MEMS陀螺仪相比于高精度陀螺仪如光纤陀螺仪以及激光陀螺仪具有更大的噪声、漂移以及非线性刻度因数,且受温度影响较大[2],导致MEMS陀螺仪的精度较低,且随着时间的增加精度逐渐降低,无法满足姿态解算及定位需求。
MEMS陀螺仪的误差主要由确定性误差及随机误差组成[3],确定性误差主要可以通过标定方法进行抑制,对于随机误差有方法提出采用卡尔曼滤波对陀螺仪数据进行误差补偿[4-5],但卡尔曼滤波中的过程噪声方差和量测噪声方差均由简单统计特性得到,无法自适应地跟随陀螺仪特性变化而变化。有研究[6]提出采用ARMA模型对陀螺仪噪声进行建模,但仍无法卡尔曼滤波中噪声方差估计的问题。针对此问题,有研究提出使用自适应Sage-Husa算法[7]进行陀螺仪误差补偿,使用前一时刻量测噪声方差结合卡尔曼滤波新息值估计下一时刻量测噪声方差,算法中加入了遗忘因子但较难实时地跟随陀螺仪特性的变化情况。有研究使用开窗法[8]对噪声方差进行估计,由于开窗法估计中窗口大小选取及新息正态性要求对于估计误差及滤波性能有着较大的影响。本文提出一种基于神经网络改进卡尔曼滤波的算法对陀螺仪信号误差进行补偿处理,并采用Allan方差分析法对实测陀螺仪数据补偿前后各项噪声进行定量分析。
1 Allan方差分析原理
Allan方差是由David Allan所提出的,主要功能是分析振荡器的频率和相位不稳定性,根据陀螺仪信号的特性,也可以采用Allan方差分析法对陀螺仪随机误差进行辨识[9]。Allan方差能够定量地对陀螺仪各项随机误差进行分析,因此可以对各算法补偿前后陀螺仪信号进行Allan方差分析,作为各补偿算法的性能评价指标。
1.1 Allan方差分析
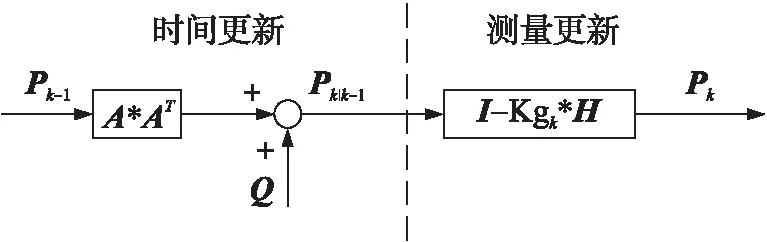
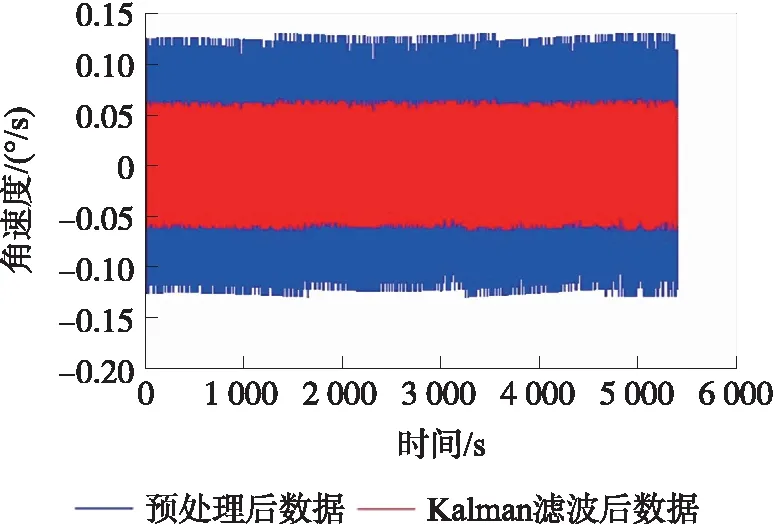
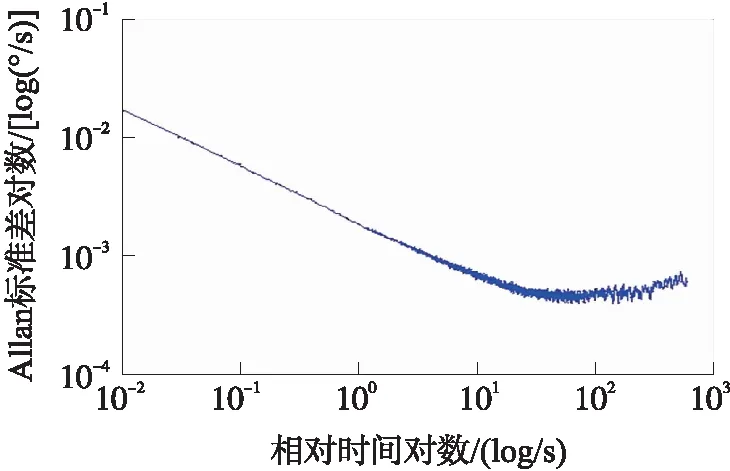
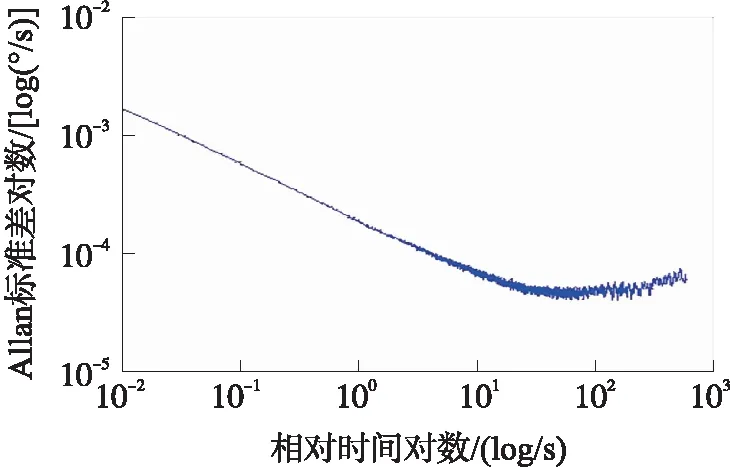
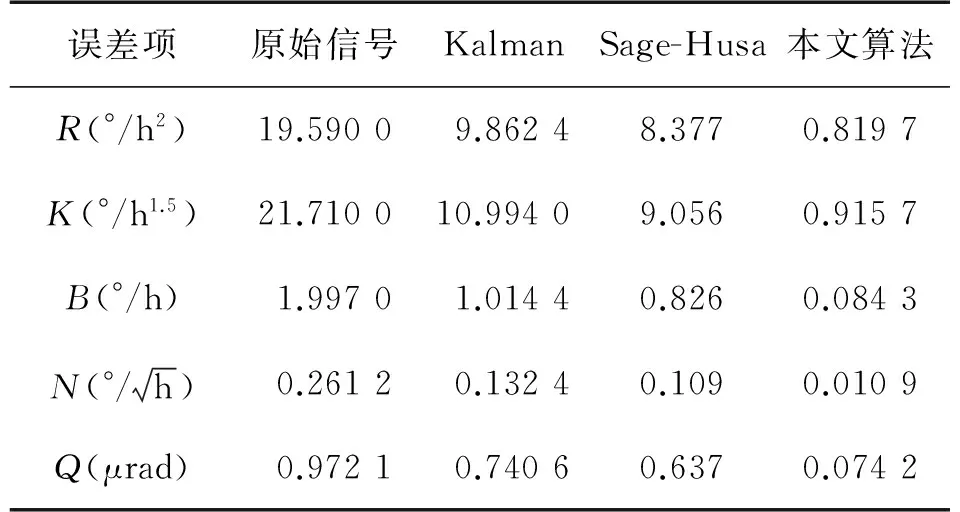
样本信号为长度N的陀螺仪数据,采样频率为f,采样时间间隔为τ0=1/f。将N个样本平均分为K组,则每一组有M=N/K个数据,每一组数据的时间长度为τ=M*τ0,该时间长度称为相关时间[10]。由于数据至少分成2组,因此M (1) 相关时间τ下的Allan方差为σ2(τ)。 (2) 取不同分组长度计算不同相关时间τ下的Allan方差σ2(τ)即可得到Allan方差曲线,Allan方差的平方根σ(τ)即为Allan标准差。 陀螺仪的总体Allan方差可以分解为各项随机噪声Allan方差求和,即 (3) (4) 用最小二乘法对Allan方差曲线进行拟合,求得各阶系数。 (5) 则可得系数与各误差项的关系如式(6)所示。 (6) 由式(6)可以求得各误差项的估计值。 (7) 陀螺仪随机噪声信号可以采用AR模型对其进行建模,AR(n)模型叫做n阶自回归模型,对N个样本的时间序列xt,其表达式如下。 xt=φ1xt-1+φ2xt-2+…+φnxt-n+at (8) 对于AR模型参数采用最小二乘法进行估计[12],能够得到无偏参数估计,计算方法简便,最小二乘法可用于估计式(9)所表示的方程组参数。 Y=Xφ+a (9) 式中: (10) 使用最小二乘法估计AR(n)模型参数公式如式(11)所示。 (11) AR模型的阶数可由AIC准则确定,当n取不同阶数时计算AIC函数值,AIC值最小时的模型为适用模型,AIC函数计算方法如式(12)所示。 (12) 卡尔曼滤波是一种基于最小均方误差准则的滤波方法,该算法主要由一组数学方程组成,通过不断迭代计算得到状态值估计,卡尔曼滤波在线性系统及高斯白噪声下是最优滤波[13]。卡尔曼滤波的主要优点是采用迭代计算方式、仅使用有限时间的数据、计算量小、实时性高。卡尔曼滤波主要被用在离散时间系统中状态量的估计,该算法核心为系统状态方程以及系统量测方程。 状态方程表示为: xk=Axk-1+Buk+wk (13) 量测方程表示为 zk=Hxk+vk (14) 式中:xk为k时刻系统状态量,uk为k时刻系统控制量,A为系统状态转移矩阵,H为系统量测矩阵,wk为系统过程噪声,vk为系统量测噪声,假定w和v为相互独立的高斯白噪声,均值为0,方差分别为Q和R。 卡尔曼滤波算法步骤如下: 第1步:计算k时刻状态一步预测值。 (15) 利用k-1时刻状态最优估计结果,由系统状态方程对k时刻x作一步预测,若系统没有控制量则取uk=0。 第2步:计算k时刻协方差一步预测。 Pk|k-1=APk-1AT+Q (16) 利用k-1时刻协方差值,计算k时刻协方差一步预测值。 第3步:计算k时刻卡尔曼滤波增益。 (17) 第4步:计算k时刻状态最优估计值。 (18) 第5步:计算k时刻协方差。 Pk=(I-KgkH)Pk|k-1 (19) 通过不断迭代执行第1步至第5步,更新各时刻状态估计值。 状态量及协方差的更新框图如图1、图2所示。 图1 卡尔曼滤波状态量更新框图 图2 卡尔曼滤波协方差更新框图 由于卡尔曼滤波中系统过程噪声及系统量测噪声方差选取困难,有方法提出采用开窗法估计过程噪声及量测噪声方差,使用当前时刻及历史时刻新息值αk利用窗估计法计算新息协方差矩阵Cαk,计算方法如式(20)所示。 (20) 在开窗法估计中窗口大小选取以及新息是否符合正态分布都容易引起估计误差,窗口选取过小会导致新息协方差矩阵具有较大噪声,窗口选取过大会导致新息协方差矩阵无法反应系统瞬间变化情况。因此本文提出在开窗法估计的思路上使用神经网络对新息协方差进行估计并计算得到系统量测噪声的方差。 2.3.1 系统量测噪声方差估计 k时刻观测量zk无法从一步预测状态中得到的部分为αk,称为新息。 (21) 将量测方程代入式(21)并对等式两边同时取协方差可得新息协方差矩阵表达式。 (22) 式中:Cαk为新息αk的协方差矩阵。 则系统量测噪声估计值与新息协方差矩阵关系如式(23)所示。 Rk=Cαk-HPk|k-1HT (23) 2.3.2 系统过程噪声方差估计 系统过程噪声方差的估计值由系统状态方程与状态估计方程相结合得到,系统过程噪声方差与新息协方差矩阵关系如下式所示。 xk=Axk-1+wk (24) (25) (26) (27) 2.3.3 神经网络改进卡尔曼滤波算法 算法采用BP神经网络,BP神经网络是一种三层神经网络,包含输入层、隐含层、输出层,其中输入层和输出层是唯一的,隐含层可以由多层组成[14]。每一层中可以有不同数量的神经元,前一层神经元连接到后一层的各个神经元,并具有不同的连接权值ω和阈值b。 BP神经网络的学习过程是一种有监督学习过程,通过不断利用输出误差来估计输出层与上一隐含层误差,再用得到的误差估计更前一层的误差,以此获得所有层的误差,并不断调整相邻层间的连接权值和阈值,已达到降低输出误差的目的。BP神经网络的训练过程主要由信号前向传播计算输出和误差反向传播调整网络参数两个过程组成。其结构图如图3所示。 图3 BP神经网络结构图 本算法首先需要对神经网络进行训练,对于不同环境不同噪声情况下的陀螺仪数据进行采样,使用AR模型建立时得到的过程噪声方差Q结合式(27)计算新息协方差矩阵Cαk作为目标输出,将对应时刻及历史时刻的卡尔曼滤波新息值组成输入矩阵[αkαk-1αk-2αk-3αk-4]T,使用MATLAB对神经网络进行训练来迭代调整神经网络的连接权值及阈值使得网络能够满足误差精度要求,得到当前时刻及历史时刻组成的新息矩阵与新息协方差矩阵Cαk之间的非线性关系。计算时使用当前时刻及历史时刻组成的新息矩阵作为神经网络的输入,新息协方差矩阵Cαk作为神经网络输出,结合式(23)使用神经网络输出的新息协方差矩阵Cαk计算系统量测噪声方差Rk,然后将量测噪声方差代入卡尔曼滤波进行误差补偿,基于神经网络改进的卡尔曼滤波算法流程图如图4所示。 图4 神经网络改进卡尔曼滤波算法流程图 图5 陀螺仪数据采集环境 实验使用MEMS三轴加速度计、陀螺仪二合一芯片MPU6050,设置陀螺仪量程为±250 (°)/s,采样频率为100 Hz,采样周期为10 ms。使用STM32通过I2C总线读取陀螺仪测量数据,并使用串口转蓝牙模块将采集所得数据通过蓝牙发送至笔记本,笔记本使用MATLAB接收蓝牙模块数据并保存,数据采集在可调速转台上进行,z轴垂直于转台平面,采集环境如图5所示。 采集过程首先打开电源将陀螺仪芯片预热20 min等待陀螺仪数据稳定,然后连续采集90 min,得到的陀螺仪z轴原始数据如图6所示。 图6 陀螺仪原始数据 对采集所得的原始数据通过标定[15]抑制确定性误差,然后使用最小二乘法提取趋势项,将整体数据减去趋势项以保证数据平稳性,最后使用拉伊达准则[16]剔除陀螺仪数据中的异常值。对预处理后的陀螺仪数据进行平稳性及正态性检验,结果显示数据满足平稳性及正态性要求。预处理后的数据如图7所示,其均值为1.453 6×10-6(°)/s,方差为0.001 8 (°)2/s。 图7 预处理后陀螺仪数据 对采样数据分别采用AR(1)、AR(2)、AR(3)模型进行建模,得到拟合系数如表1所示。 表1 AR模型系数 由表1数据计算得到各阶AR模型的AIC值为AIC(1)=-6.298 7、AIC(2)=-6.298 4、AIC(3)=-6.298 3,AR(1)模型的AIC值最小,因此采用AR(1)模型对陀螺仪信号进行建模,其表达式如式(28)所示。 (28) 对陀螺仪信号使用AR模型建模作为卡尔曼滤波的状态方程,取状态一步预测值作为量测估计值,则卡尔曼滤波的系统方程如下式所示。 xk=0.0187xk-1+wk (29) zk=xk+vk (30) (31) 对陀螺仪数据采用卡尔曼滤波进行误差补偿结果如图8所示,其均值为-7.321 1×10-7(°)/s,方差为4.441 9×10-4(°)2/s2。 图8 卡尔曼滤波误差补偿后陀螺仪数据 针对卡尔曼滤波中量测噪声方差选取不准确的问题使用新息协方差矩阵估计量测噪声,使用开窗法通过当前时刻及历史时刻新息矩阵计算新息协方差矩阵Cαk,并引入渐消因子。 dk=(1-b)/(1-bk+1),0 (32) (33) 实验中取b=0.99对陀螺仪数据采用Sage-Husa滤波进行误差补偿,结果如图9所示,其均值为8.7432×10-6(°)/s,方差为3.0542×10-4(°)2/s2。 图9 Sage-Husa滤波误差补偿后陀螺仪数据 首先对神经网络进行训练,使用将不同环境下的卡尔曼滤波新息矩阵作为输入,新息协方差矩阵作为目标,使用MATLAB工具箱构建一个隐含层具有5个神经元的神经网络。 隐含层各神经元阈值bh,输入层与隐含层的连接权值wih、输出层各神经元阈值co以及隐含层与输出层的连接权值vho分别如式(34)~式(37)所示。 b=[-2.81 -0.53 -0.32 0.46 2.93]T (34) (35) c=-0.79 (36) v=[-0.01 -0.01 0.001 0.003 -0.22] (37) 图10 神经网络改进卡尔曼滤波误差补偿后陀螺仪数据 将所采集的陀螺仪数据使用本文提出的神经网络改进卡尔曼滤波算法进行误差补偿,使用神经网络对于系统量测噪声依据信息值进行动态估计,误差补偿后的陀螺仪数据如图10所示,其均值为9.625 9×10-8(°)/s,方差为3.007 2×10-6(°)2/s2。 使用Allan方差分析法分别对陀螺仪原始数据、标准卡尔曼滤波算法误差补偿后数据、Sage-Husa滤波算法误差补偿后数据以及本文提出的神经网络改进卡尔曼滤波算法误差补偿后数据进行计算,并绘制Allan标准差曲线。4组数据的Allan标准差曲线分别如图11~图14所示。 图11 原始数据Allan标准差曲线 图12 卡尔曼滤波误差补偿后数据Allan标准差曲线 图13 Sage-Husa滤波误差补偿后数据Allan标准差曲线 图14 神经网络改进卡尔曼滤波误差补偿后数据Allan标准差曲线 使用最小二乘法对计算所得的各Allan标准差曲线进行拟合,得到各误差项估计值,结果如表2所示。 表2 不同补偿算法结果各误差项统计表 由表2可以看出本文所提出的神经网络改进卡尔曼滤波误差补偿算法相比于标准卡尔曼滤波误差补偿算法有较大性能提高,各误差项估计值都大幅降低。其中速率斜坡R降低了91.69%,角速率随机游走K降低了91.67%,零偏不稳定性B降低了91.68%,角随机游走N降低了91.69%,量化噪声Q降低了89.96%。Sage-Husa滤波算法同样针对量测噪声方差选取问题,本文提出的算法相比于该算法具有较大性能提升,实验表明利用神经网络能够更好地拟合当前时刻及历史时刻新息矩阵与新息协方差之间的关系,更准确地估计新息协方差矩阵以及系统量测噪声方差,但神经网络的训练过程需要消耗一定的训练时间,并且需要针对每个芯片进行大量数据的采集及训练,牺牲了时间及计算复杂度,获得了更高的性能提升。 由于在惯性导航中通常利用陀螺仪来确定载体姿态,需要陀螺仪具有较高的精度,但MEMS陀螺仪相较于高精度陀螺仪具有更大的噪声干扰,因此提出采用噪声误差补偿算法对陀螺仪信号误差进行补偿。本文首先介绍了Allan方差分析法在陀螺仪噪声辨识中的应用,然后对信号建模方法进行了介绍,并介绍了利用卡尔曼滤波方法在该信号模型下的误差补偿算法。通过分析标准卡尔曼滤波以及开窗法Sage-Husa滤波中的缺点,本文提出了采用神经网络对系统量测噪声进行估计的方法,将卡尔曼滤波得到的新息矩阵作为神经网络输入,通过训练好的神经网络输出为新息协方差矩阵的估计值,使用新息协方差矩阵可以计算出系统量测噪声估计值,并将其代入到卡尔曼滤波中进行误差补偿。实验表明本文提出的陀螺仪误差补偿算法相比于标准卡尔曼滤波算法以及Sage-Husa滤波算法都具有更好的补偿效果,使用Allan方差分析法对滤波前后陀螺仪信号进行定量分析可以看出各随机误差项估计值均大幅降低,有效提高陀螺仪精度。 参考文献: [1] 李杰,张文栋,刘俊. 基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究[J]. 传感技术学报,2006,(05):2215-2219. [2] SONG L,ZHANG W. Temperature Error Compensation for Open-Loop Fiber Optical Gyro Using Back-Propagation Neural Networks with Optimal Structure[C]//Proceedings of the Proceedings of 2014 IEEE Chinese Guidance,Navigation and Control Conference,F 8-10 Aug. 2014,2014. [3] 霍元正. MEMS陀螺仪随机漂移误差补偿技术的研究[D]. 南京:东南大学,2015. [4] 张玉莲,储海荣,张宏巍,等. MEMS陀螺随机误差特性研究及补偿[J]. 中国光学,2016(4):501-510. [5] Yan X,Wenjie C,Wenhui P. Research on Random Drift Modeling and a Kalman Filter Based on the Differential Signal of MEMS Gyroscope[C]//Proceedings of the 2013 25th Chinese Control and Decision Conference(CCDC),F 25-27 May 2013,2013. [6] 孙伟,文剑,张远,等. MEMS陀螺仪随机误差的辨识与降噪方法研究[J]. 电子测量与仪器学报,2017(1):15-20. [7] 李杰,郑伦贵,王建中. 陀螺漂移误差建模与滤波[J]. 传感技术学报,2017,30(5):731-734. [8] 高怡,高社生. 抗差自适应Sage滤波及其在组合导航中的应用[J]. 测控技术,2015(4):135-138,141. [9] 邹学锋,卢新艳. 基于Allan方差的MEMS陀螺仪性能评价方法[J]. 微纳电子技术,2010(8):490-493,498. [10] 蒋孝勇,张晓峰,李孟委. 基于Allan方差的MEMS陀螺仪随机误差分析方法[J]. 测试技术学报,2017(3):190-195. [11] Cao H,Lü H,Sun Q. Model Design Based on MEMS Gyroscope Random Error[C]//Proceedings of the 2015 IEEE International Conference on Information and Automation,F 8-10 Aug. 2015,2015. [12] 陈国强,赵俊伟,黄俊杰,等. 基于MATLAB的AR模型参数估计[J]. 工具技术,2005(4):39-40. [13] Chia J W,Tissera M S C,Low K S,et al. A Low Complexity Kalman Filter for Improving MEMS Based Gyroscope Performance[C]//Proceedings of the 2016 IEEE Aerospace Conference,F 5-12 March 2016,2016. [14] 刘彩红. BP神经网络学习算法的研究[D]. 重庆:重庆师范大学,2008. [15] 彭孝东,陈瑜,李继宇,等. MEMS三轴数字陀螺仪标定方法研究[J]. 传感器与微系统,2013,26(6):63-65,69. [16] 张敏,袁辉. 拉依达(PauTa)准则与异常值剔除[J]. 郑州工业大学学报,1997(1):87-91. 李鲁明(1993-),男,上海人,硕士研究生,通信与信息系统专业,主要研究方向为惯性导航系统,组合导航信息融合算法研究,luming.li@mail.sim.ac.cn; 赵鲁阳(1970-),男,江苏人,博士,副研究员,主要研究方向为无线传感网络应用,围界防入侵,数字信号处理等; 唐晓红(1994-),女,江苏人,硕士研究生,通信与信息系统专业,主要研究方向惯性导航系统,组合导航信息融合算法研究; 何为(1981-),男,福建人,博士,副研究员,主要研究方向为无线传感网络应用,数字信号处理等。

1.2 Allan方差分析法陀螺仪噪声辨识
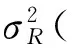
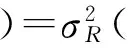

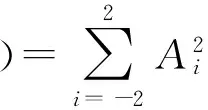
2 陀螺仪误差补偿算法
2.1 信号模型建立
2.2 卡尔曼滤波原理

2.3 神经网络改进卡尔曼滤波陀螺仪误差补偿算法
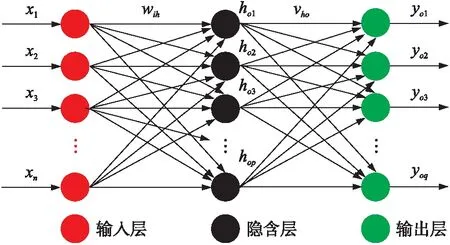


3 实验数据及结果分析
3.1 陀螺仪数据采集及预处理


3.2 陀螺仪数据建模
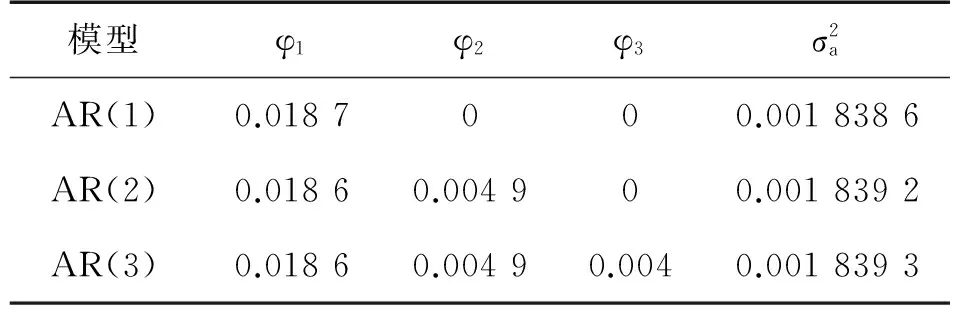
3.3 卡尔曼滤波陀螺仪误差补偿算法实验
3.4 Sage-Husa自适应滤波误差补偿算法实验
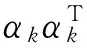

3.5 神经网络改进卡尔曼滤波误差补偿算法实验


3.5 基于Allan方差分析的各补偿算法对比


4 结论





