无线传感网络中目标定位的研究*
张 锐
(驻马店职业技术学院信息工程系,河南 驻马店 463000)
无线传感网络WSNs(Wireless Sensor Networks)被广泛应用于收集环境数据,如温度、湿度和气压等。这些数据与位置信息息息相关,无准确位置的数据没有实用价值。据此,位置信息成为WSNs多项应用的关键。因此,定位成为WSNs应用的基本技术,也成为WSNs研究热点[1]。
作为新的信号抽样理论,压缩感知CS(Compressive Sensing)[2-3]能够利用少数的抽样值恢复稀疏信号。由于目标数有限(一般较少),可利用CS算法,并结合少的抽样值进行目标位置估计。文献[4-8]就提出基于CS的定位算法。这些算法将连续物理空间划分离散网格。在估计目标位置时,它们先假定所有目标均准确地落在预定的网格上,再将测量的信号值代表网格点,最后利用表示系数对这些目标位置进行编码。因此,定位过程可看成重构稀疏表示系数的过程。
然而,假设所有目标均准确地落在预定的网格上,这种假设不切实际。换而言之,物理空间是连续的,而抽样后的网格是离散的。此外,在WSNs中是无法提前预测目标数量和它们的位置。
此外,这些基于CS的目标定位算法的复杂度是无法预计的。由于网格极度密集,算法的复杂度非常大。因此,这些算法一定存在假设与实际情况间的不匹配问题。现存的研究表明,这些不匹配极大地降低CS算法的性能[9-11]。
与传统的基于CS的目标定位算法不同,本文提出基于变分贝叶斯期望最大化的目标定位VBEM-TL(Variational Bayesian Expectation Maximization-based Target Localization)算法。VBEM-TL算法先利用一阶泰勒扩展系数建立稀疏近似模型,然后引用变分贝叶斯期望最大化(Variational Bayesian Expectation Maximization,VBEM)算法重构稀疏矢量,最后估计目标位置。
实验数据表明,提出的VBEM-TL算法能够有效地降低定位误差。
1 网络模型与问题描述
1.1 网络模型
考虑在二维区域内进行多目标定位问题。每个目标携带了无线发射设备,进而它能周期地广播信号。而二维区域内一些传感节点测量来自目标信号的接收信号强度RSS(Received Signal Strength)。实际上,传感节点所接收的信号是来自多个目标信号的叠加。据于此事实,将每个RSS值看成多个不同目标信号之和。

因此,第m个传感节点所接收的RSS值可表示为:
(1)
式中:αk、εk分别表示发射功率和加性噪声。而f(tm,θk)表示能量衰减函数,其由环境决定。
对式(1)进行矢量-矩阵表述,如式(2)所示:
z=D(Θ)·α+ε
(2)
式中:z=[z1,z2,…,zM]T,α=[α1,α2,…,αK]T。ε=[ε1,ε2,…,εM]T,D(Θ)=[d(θ1),…,d(θK)]。而d(θk)=[f(t1,θk),…f(tM,θk)]T。
1.2 问题描述


(3)
式中:w=[ω1,…,ωN]T表示表示系数。
由于目标数远远小于网格点数,这个表示系数w是稀疏矢量。如果第k个目标落在于第i个网格点,则ωi=ak,否则ωi=0。因此,定位问题就可转化为稀疏重构问题。
2 VBEM-TL算法
整个VBEM-TL定位算法由3个部分过程,首先依据一阶泰勒级数(Taylor)展开算法建立稀疏模型,然后再依据VBEM算法重构稀疏矢量,最后依据重构的稀疏矢量估计目标位置,如图1所示。

图1 VBEM-TL定位算法的流程框图
2.1 稀疏近似模型

(4)
因此,D(Θ)和测量矢量z的近似值,可表示为:
(5)
(6)
式(6)所示的近似信号模型,可表述为:
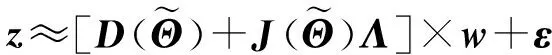
(7)
令v=Λw∈R2N×1,式(7)的稀疏近似模型可以写成为:
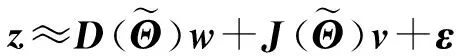
(8)
接下来,利用变分贝叶斯期望最大化VBEM(Variational Bayesian Expectation Maximization)[12]算法重构矢量w和v。将w和v作为两个统计变量,再利用VBEM算法将w和v更新成为latent 变量。
2.2 表示系数的更新
利用VBEM算法重构矢量w和v的模型如图2所示。

图2 VBEM的模型
依据这个模型,VBEM-TL算法引用矢量w的先验知识去推导稀疏矢量。令αi表示矢量w的第i个元素的先验逆变量。因此,矢量w的先验分布可表示为:
(9)
式中:α=[α1,α2,…,αN]T,A=diag(α)。
由于Gamma分布是高斯分布的共轭,可利用Gamma分布表述矢量α。因此,矢量α的先验分布定义为:
(10)
式中:Gamma(·|a,b)表示关于参数a、b的Gamma分布。
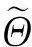
(11)
依据式(11),可得变量λn的取值范围:
(12)
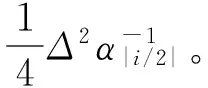
(13)
式中:B=4Δ-2diag(α⊗12×1)。
类似地,假定测量噪声是独立、高斯分布,且均值为零,方差为β-1,如式(14)所示:
(14)
并且:p(β;c,d)=Gamma(β|c,d)。
依据式(8)和式(14),可得关系函数:

(15)
利用VBEM算法,可分别得到矢量w、ν、α和β的后验分布,分别如下所示:
lnq(w) =〈lnp(z,w,v,α,β)〉q(v)q(α)q(β)+C1
=〈lnp(z|w,v,β)p(w|a)〉q(v)q(α)q(β)+C1
(16)
lnq(v) =〈lnp(z,w,v,α,β)〉q(w)q(α)q(β)+C2
=〈lnp(z|w,v,β)p(v|a)〉q(w)q(α)q(β)+C2
(17)
lnq(α) =〈lnp(z,w,v,α,β)〉q(w)q(α)q(β)+C3
=〈lnp(w|α)p(v|α)p(α))〉q(w)q(v)+C3
(18)
lnq(β) =〈lnp(z,w,v,α,β)〉q(w)q(α)q(β)+C4
=〈lnp(z|w),v,β)p(β)〉q(w)q(v)+C4
(19)
式中:C1、C2、C3和C4分别表示常数。
因此,可得:
q(w)=N(w|μw,∑w)
(20)
q(v)=N(v|μv,∑v)
(21)
(22)

(23)
式中:
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
2.3 重构稀疏过程
利用上述推导结果,可以对表示系数sw和v进行更新,算法1的伪代码如图3所示。

图3 重构稀疏的伪代码
然后,计算第k+1次迭代值rk+1:
(32)
再计算第k次与第k+1次迭代值的差Δr:
Δr←|rk+1-rk|
(33)
通过不断地迭代,直到误差Δr满足:
Δr=|rk-rk-1|≤η
(34)

2.4 定位算法
(35)
(36)
式中:δ为较小的稀疏门限。而Ik表示最靠近第k个目标的网格点的估计值的下标。
3 性能仿真
3.1 仿真环境
考虑面积为90 m×90 m的二维区域,且K个目标和M个传感节点随机分布于此二维区域。将此区域划分N个均匀的网格。同时,设定η=10-6、δ=0.8,而a1=a2…=aK=100 mW。
为了更好地分析VBEM-TL的性能,选择BP(Basic Pursuit)和正交匹配搜索OMP(Orthogonal Matching Pursuit)和贝叶斯压缩感知BCS(Bayesian Compressive Sensing)进行同步仿真,并进行性能比较。
3.2 数值分析
首先分析在无噪声,且K=4,M=25和N=100环境下,VBEM-TL算法的定位准确性。
从图4可知,BP算法的定位误差最大,而VBEM-TL算法的定位误差最低,它所估计的目标位置贴近其真实位置。而其他算法所估计的目标位置与真实位置还存在距离。这些数据表明,提出的VBEM-TL算法能够准确地估计目标位置。
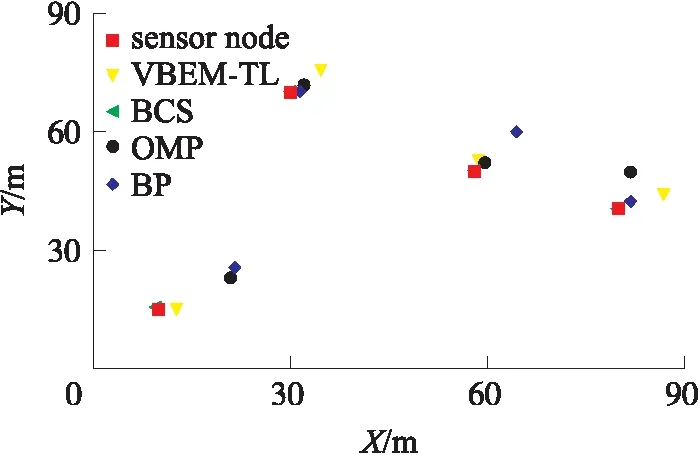
图4 4个目标定位示意图
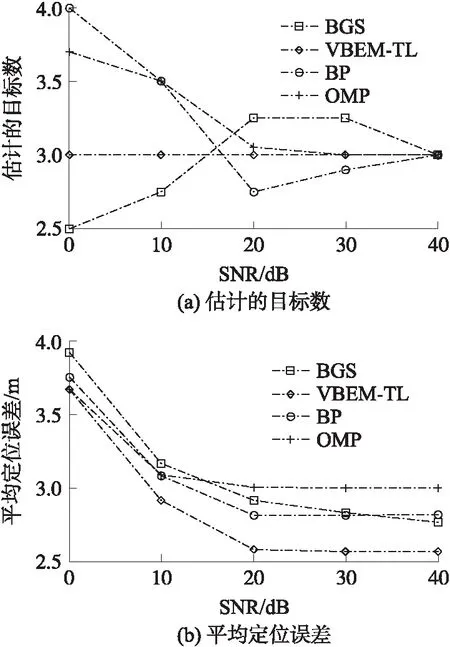
图5 信噪比对定位性能的影响
接下来,分析在噪声环境下,VBEM-TL算法的定位性能。实验环境为:K=3,M=25和N=100,信噪比SNR从0至40 dB变化,估计的目标数和平均定位误差随信噪比SNR的变化曲线如图5所示。
图5(a)表示了信噪比SNR从0至40 dB变化时,所估计的目标数的平均值。而图5(b)表示了信噪比SNR从0至40 dB变化时,所估计的目标数的平均定位误差。从图5(a)可知,SNR的增加,有利于定位性能的提高。而图5(b)数据表明,提出的VBEM-TL算法的平均定位误差最低,并且随着SNR的提高,VBEM-TL算法的性能越好。
最后,分析传感节点数对定位性能的影响。实验环境为:K=5,SNR=25 dB和N=256,M从50至64变化。估计的目标数和平均定位误差随随节点数M的变化曲线如图6所示。
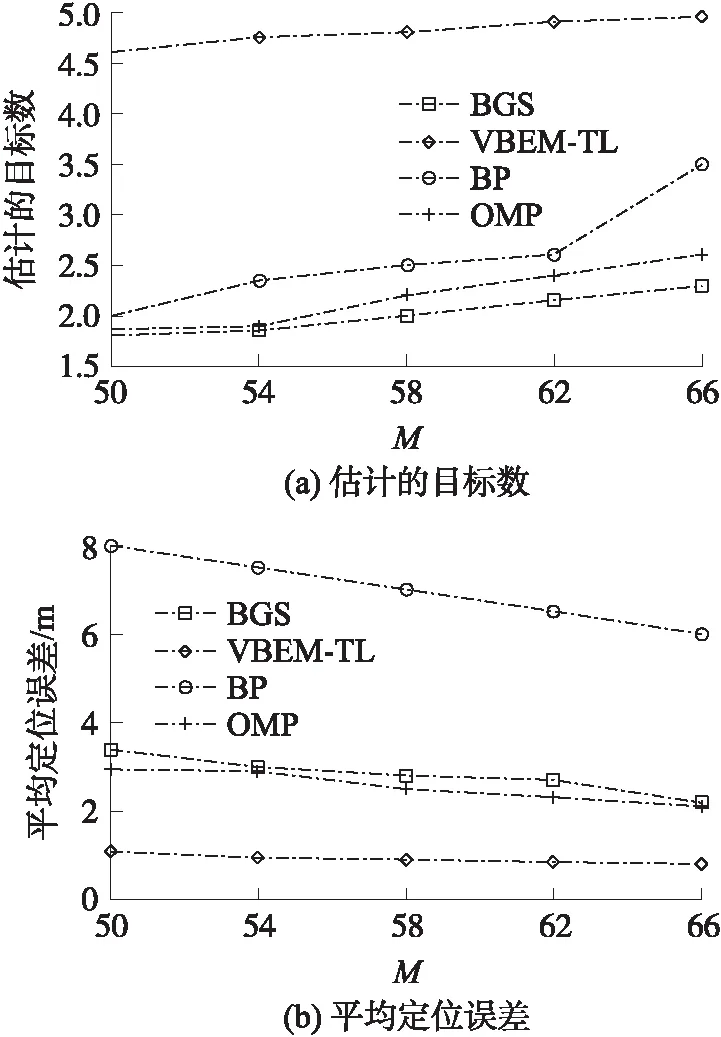
图6 传感节点数对定位性能的影响
从图6可知,传感节点数M的增加有利于定位准确性的提高,原因在于稀疏重构准确率正比于M。更为重要的时,相比BP、OMP和BCS相比,VBEM-TL算法的定位性能得到有效地提高。原因在于VBEM-TL算法能够准确地重构稀疏矩阵。
4 总结
本文针对无线传感网络中目标定位问题,提出基于变分贝叶斯期望最大化的目标定位VBEM-TL算法。
VBEM-TL算法先利用VBEM重构稀疏矢量,再追踪目标位置。实验数据表明,提出的VBEM-TL能够有效地估计目标位置。
参考文献:
[1] Dai W,Shen Y,Win M Z. Distributed Power Allocation for Cooperative Wireless Network Localization[J]. IEEE J Sel Areas Commun,2015,33(1):28-40.
[2] Donoho D L. Compressed Sensing[J]. IEEE Trans Inf Theory,2016,52(4):1289-1306.
[3] 朱路,刘媛媛,慈白山,等. 多稀疏基分簇压缩感知的WSN数据融合方法[J]. 传感技术学报,2016,29(3):417-222.
[4] Cevher V,Duarte M F,Baraniuk R G. Distributed Target Localization via Spatial Sparsity[C]//Proc 16th Eur Signal Process Conf,Aug. 2014:1-5.
[5] 刘洲洲,徐继良. 基于压缩感知理论的WSNs时序信号分段压缩算法[J]. 传感技术学报,2016,29(1):122-128.
[6] Zhang B,Cheng X,Zhang N,et al. Sparse Target Counting and Localization in Sensor Networks Based on Compressive Sensing[C]//Proc IEEE INFOCOM,Apr. 2014:2255-2263.
[7] Wu D,Arkhipov D I,Zhang Y,et al. Online War-Driving by Compressive Sensing[J]. IEEE Trans Mobile Comput,2015,14(11):2349-2362.
[8] Lagunas E,Sharma S K,Chatzinotas S,et al. Compressive Sensing Based Target Counting and Localization Exploiting Joint Sparsity[C]//Proc IEEE Int Conf Acoust,Speech Signal Process(ICASSP),Mar. 2016:3231-3235.
[9] Herman M,Strohmer T. General Deviants:An Analysis of Perturbations in Compressed Sensing[J]. IEEE J Sel Topics Signal Process,2014,4(2):342-349.
[10] Ihsan Ilhan,Ali Cafer G. Compressive Sensing-Based Robust off-the-Grid Stretch Processing[J]. IET Radar,Sonar and Navigation,2017,11(1):1730-1735.
[11] Chi Y,Scharf L L,Pezeshki A,et al. Sensitivity to Basis Mismatch in Compressed Sensing[J]. IEEE Trans Signal Process,2014,59(5):2182-21951.
[12] Tzikas D G,Likas A C,Galatsanos N P. The Variational Approximation for Bayesian Inference[J]. IEEE Signal Process Mag,2014,25(6):131-146.

