改进型萤火虫算法求解CRN频谱分配问题
徐婷婷 孙文胜
(杭州电子科技大学通信工程学院 浙江 杭州 310018)
0 引 言
在认知无线电网络CRN中,频谱分配方案多种多样,其目的既要防止次用户对主用户的干扰和次用户互相之间的自干扰,并且要实现高可靠高效率的通信。因此,选择一种合理高效的频谱分配算法尤其重要[1-3]。
萤火虫GSO算法是模拟自然界中成虫发光的生物学特性发展而来的,也是基于群体的随机优化算法,由印度学者Krishnanand等提出[4]。各个萤火虫以寻优为目的,在其搜索范围内寻找最亮的萤火虫,进而向最亮的萤火虫移动。但在GSO算法中[5-7],萤火虫的移动步长是固定的,容易使算法陷入局部最优解,搜索精度低,并且其适应度函数值可能会有震荡现象。
因此,提出改进型萤火虫算法IGSO(Improved Glowworm Swarm Optimization),使固定步长改为自适应可变步长来增强算法收敛速度和精度,提升算法的稳定性,且使用混沌搜索法优化部分个体来提高算法全局探索性。
1 基本萤火虫算法
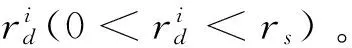
1) 荧光素更新阶段:
li(t+1)=(1-ρ)li(t)+γ·F(Xi(t+1))
(1)
式中:ρ∈(0,1)为荧光素变化率,γ为萤火虫适应度函数变化率,F(Xi(t+1))为适应度函数。
2) 位置更新阶段:
在领域半径内,萤火虫i以概率pij向萤火虫j移动。
(2)
选定同伴j后,按照下式更新空间坐标:
(3)
式中:d是各萤火虫的固定移动步长,‖·‖是萤火虫i和其同伴j之间的欧式距离。
3) 动态领域半径更新阶段:
在更新坐标后,各个萤火虫会通过自身搜索空间中的同伴集合的个数动态调整领域半径的大小。
(4)
式中:nt为萤火虫数量控制阈值,β为控制系数,Ni(t)为领域半径内相比萤火虫i荧光素更高的个体数目,rs为最大领域半径。
2 改进型萤火虫算法
2.1 自适应搜索步长
在IGSO算法中,针对GSO算法存在的缺陷,把固定移动步长d转为自适应移动步长s(t),改进后s(t)为:
(5)
(6)
式中:δi为自适应协调因子,Xmax为此次迭代中荧光素最大的萤火虫所在空间位置;smin和smax为最小、最大移动步长,t为本次迭代数,tmax为最大迭代次数,m为空间维度。
自适应协调因子,随着距离的增大而增大。改进后的自适应移动步长根据两个萤火虫个体之间的距离和迭代次数进行自适应调整。若两个体之间实际距离过大,且在初始阶段萤火虫移动步长也增大,随着后期迭代次数增加,自适应移动步长受约束,萤火虫移动步长会适当减小。因此,改进后的萤火虫算法不会由于搜索步长过大跳过最优解,也不会在初始阶段由于移动步长太小而影响搜索速度,整体上提高了搜索速度和精度。
2.2 混沌搜索策略
混沌现象是指发生在确定性系统中的貌似随机的不规则运动,其具有遍历性、规律性、随机性的特点,通过其自身的内在规律可以不重复地遍历所有状态[8-9]。在萤火虫算法中,当个体在领域半径内长时间寻优后,会陷入局部最优解,其适应度函数不再改变。因此,利用混沌搜索生成新解来优化部分个体,从而提高算法全局优化能力。
由于立方混沌映射产生的混沌序列分布较均匀,遍历性较高,只要初值不为0,即会产生混沌现象[10]。因此,本文采用立方混沌作为搜索策略。其数学表达式为:
(7)
位置更新为:
(8)

2.3 IGSO算法实现步骤
1) 初始设置。将n只萤火虫进行随机分散于m维搜索空间里。每只萤火虫初始荧光素为l0和初始领域半径为r0,最大领域半径为rs,码距最大值为smax,码距最小值为smin,荧光素变化率为ρ,最大迭代次数为N,适应度变化率为γ,控制系数为β,数量控制阈值为nt。
2) 执行IGSO算法进行搜索:
(1) 荧光素计算。根据式(1)计算所得荧光素值,若满足li(t+1)≥li(t),则转至(2)。
(2) 计算Ni(t)个数。在自身的领域半径内,比自身荧光素大的萤火虫组成领域集,计算其个数。
(3) 计算移动概率pij,根据式(2)计算萤火虫i在领域半径内其他萤火虫j接近的概率。
(4) 位置更新。由式(5)代入式(3),更新萤火虫位置。
(5) 混沌优化。若某个萤火虫连续3次适应度函数值不变,则根据式(7)、式(8)进行个体替换。
(6) 更新领域半径。根据式(4)更新动态领域半径。
3) 判断是否达到最大迭代次数N,若是跳到4)直接输出,反之,跳回到2)继续搜索。
4) 输出结果,程序结束。
由上述实现步骤得出基本流程,见图1。
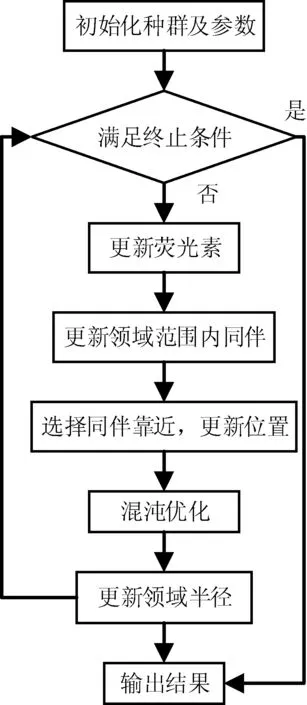
图1 基于IGSO算法流程图
3 认知无线电频谱分配模型
设认知无线电网络有N个次用户(标号为1-N),M个可用频谱(标号为1-M)。其模型由以下部分矩阵组成[3,11-12]。
1) 频谱效益矩阵:
B={bn,m}N×M
(9)
B矩阵用来表示各次用户占用当前频谱所取得的效益;bn,m表示次用户n在频谱m上所得最大效益。
2) 无干扰频谱分配矩阵:
A={an,m|an,m∈{0,-1},an,m≤ln,m}N×M
(10)
A矩阵用来表示系统一次无干扰频谱分配。当an,m=1时表示次用户n可以在无干扰情况下占用频谱m。
最大化网络总效益MSR(Max Sum Reward),其公式表示为:
(11)
基于认知无线电频谱分配模型研究频谱分配方案,本文利用平均最大化网络总效益(MSRM)的倒数为适应度函数以初始化萤火虫的荧光素值,通过MSR和MSRM分别比较GSO和IGSO算法。
(12)
仿真时频谱效益矩阵bn,m由萤火虫随机初始位置得出,无干扰矩阵an,m由随即产生的二元对称矩阵得出。假设在进行频谱资源分配时,用户的位置和可用的频谱资源等环境条件都是静态的。
4 仿真及结果分析
4.1 标准测试函数最优值求解
本文实验中参数设置如下: 萤火虫个数为n=50,频谱为m=10,初始萤光素为l0=5,领域半径为r0=10,最大领域范围为rs=10,最小步长为smin=0.01,最大步长为smax=1,适应度变化率为γ=0.6,萤光素变化率为ρ=0.4,最大迭代次数为N=200,控制系数为β=0.08,数量控制阈值为nt=5。粒子群算法PSO(Particle Swarm Optimization)种群个数为n=50,权重为ω=0.5,学习因子为c1=c2=2。
为验证算法的可行性。本实验选取以下4个标准测试函数对GSO算法、IGSO算法及PSO算法进行测试比较[7,13]。选用的4个标准测试函数为:
仿真结果如表1、表2所示。通过20次独立实验可以得出以下结论:第一,对比表2中的平均迭代次数,IGSO算法接近最优值的平均迭代次数均小于GSO算法和PSO算法,表明该算法的收敛速度较快。第二,对比最优值一列,在三种算法中,IGSO算法是最接近表1给出的标准函数的最小值,F1(x)为0.02,F2(x)为0.14,F3(x)和F4(x)均为0。即使PSO算法在F3(x)和F4(x)函数得出的最优值几乎接近于0,但其迭代次数高,效率低。由此可知,IGSO算法在求解精度上为三者最优。第三,从表中对比最差值和平均值可知,在F1(x)和F2(x)函数中,PSO算法远不及GSO算法,其所得解最不稳定,幅度相差较大;在F3(x)和F4(x)函数中,GSO算法为四者搜索能力最差。相比可得,IGSO算法在四个标准函数测试中,算法能力最优,稳定性最好。以上可得,在求解高纬度函数中,IGSO算法在收敛速度、求解精度及迭代过程稳定性等方面均优于GSO算法和PSO算法。
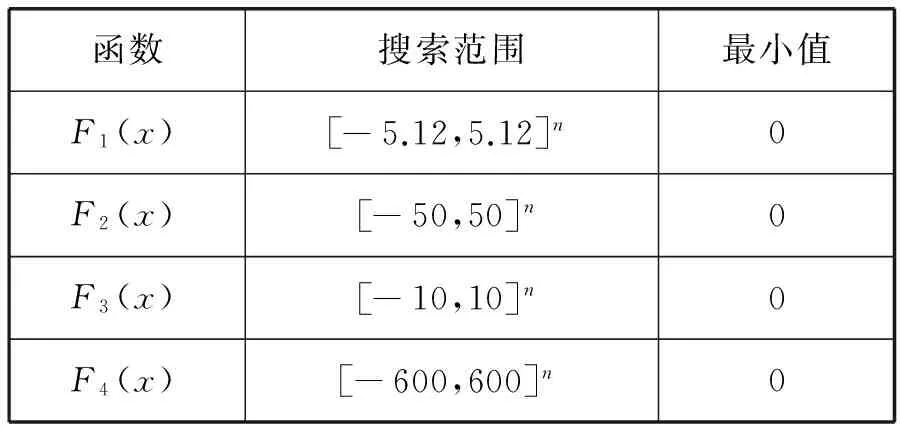
表1 标准测试函数F1(x)~F4(x)搜索范围与最小值
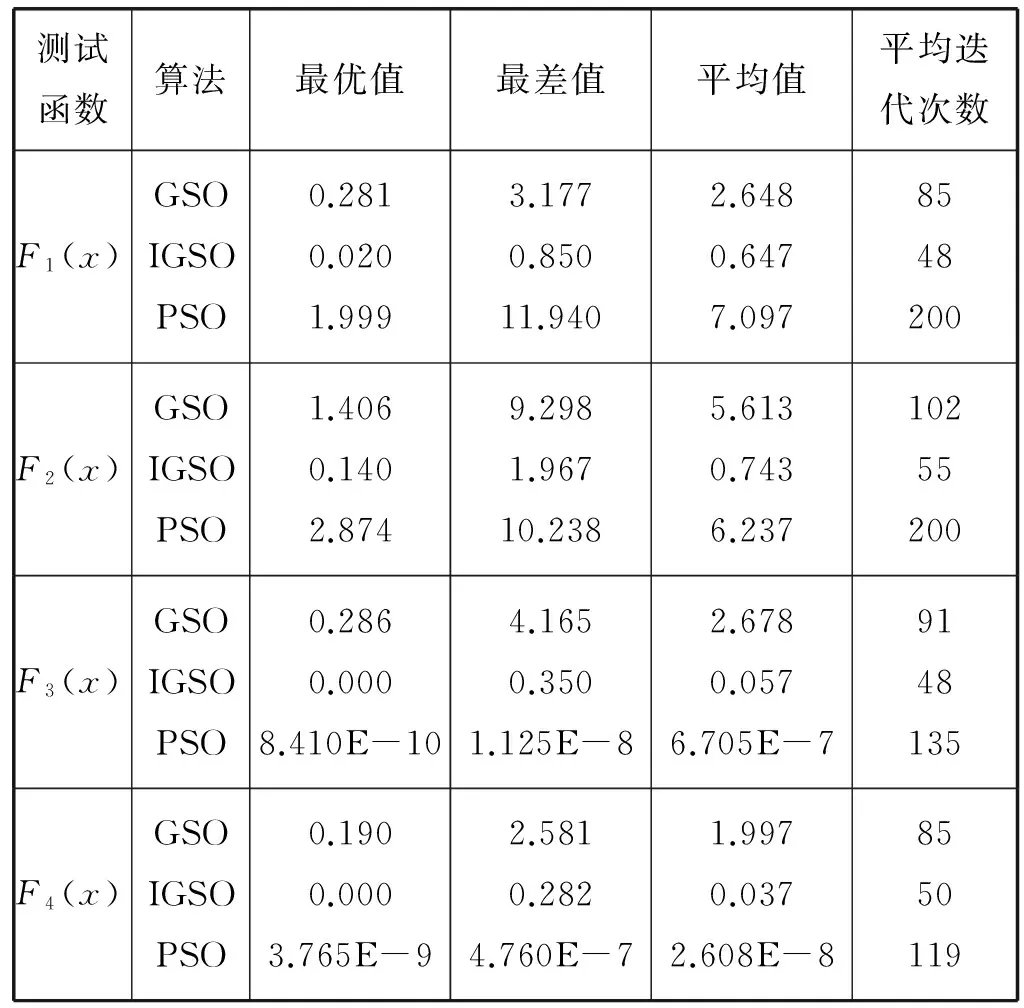
表2 GSO、IGSO算法和PSO算法性能测试指标
图2-图5为GSO算法、IGSO算法在求解标准测试函数F1(x)~F4(x)的最优解时算法寻优的变化曲线。
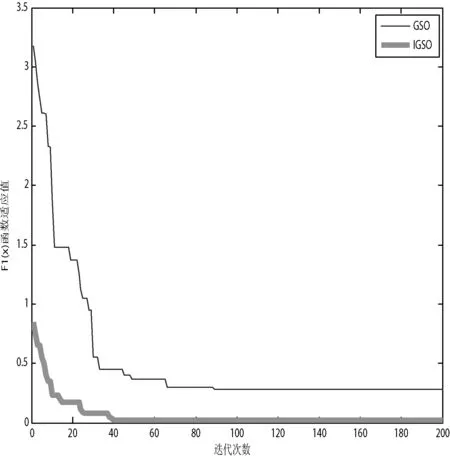
图2 F1(x)函数值寻优变化曲线
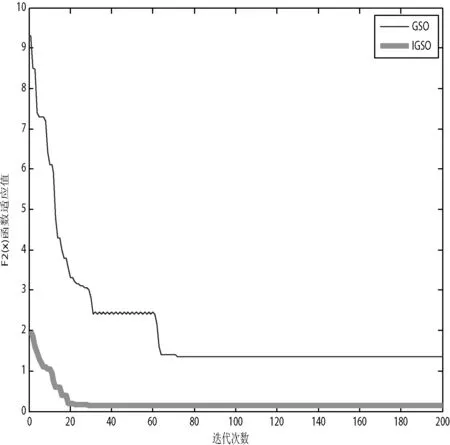
图3 F2(x)函数值寻优变化曲线
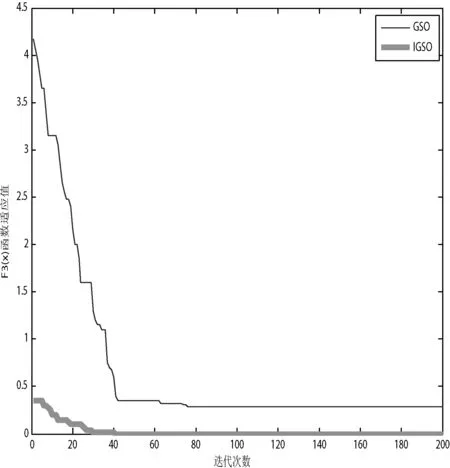
图4 F3(x)函数值寻优变化曲线
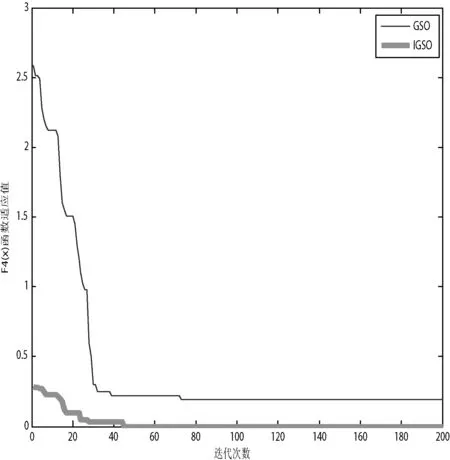
图5 F4(x)函数值寻优变化曲线
由图2-图5可知,GSO算法和IGSO算法在曲线趋于平缓后,IGSO算法在四个标准函数中,其曲线最接近X轴,即最接近最小值。并且显而易见,图中IGSO算法是最快到达横轴X,即最快得出最小值。在图3求解F2(x)函数最优值过程中,GSO算法寻优变化曲线在迭代次数35~60附近有轻微震荡的现象,这表明GSO算法所用的固定移动步长容易陷入局部最优,降低了搜索效率。而IGSO算法在能在初期寻优时更加快速,并且不易陷入局部最优,更有快达到全局最优,比较前者算法有较大改进。
4.2 GSO、IGSO算法效益比较分析
将GSO算法和IGSO算法在网络总效益和平均网络总效益上进行比较。
图6认知用户数为N=30,频谱数为M=10时,随着实验次数的增加,以最大化网络总效益UMSR为目标函数的仿真结果。从网络总效益方面来看,基于IGSO算法的频谱分配总效益曲线在总体上优于GSO算法,且起伏较小,相对稳定。
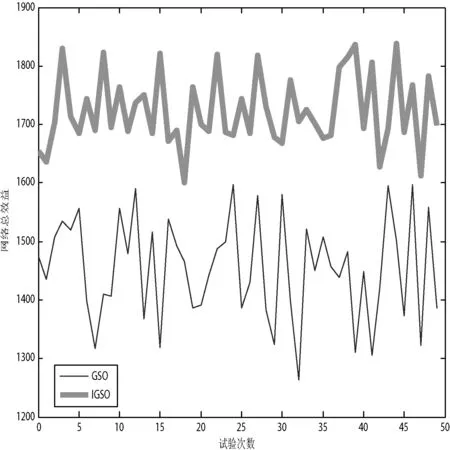
图6 GSO、IGSO的网络总效益
图7在频谱M=30时,平均网络总效益UMSRM随着次用户数N在10~30之间不断增加的变化曲线。从图中可得,基于IGSO算法的频谱分配所得到的平均网络总效益明显优于基于GSO算法的频谱分配的平均网络总效益,并且随着N的逐渐增大,优势更加明显。

图7 次用户数N变化时的平均网络总效益
图8为次用户N=10时,平均网络总效益UMSRM随着频谱数M在10~30之间不断增加的变化曲线。从图中可得,其结论与从图7得出的结论一致,IGSO算法仍为优于GSO算法。
5 结 语
本文提出了一种新型的萤火虫算法。该算法将固定步长转换为可变步长,克服了步长过大导致搜索精度不高以及步长过小降低搜索速度的缺陷。并且当算法陷入局部最优时,通过混沌优化,增强全局探索性。通过四个标准测试函数实验可知,该算法在寻优精度、收敛速度及稳定性等方面的性能均有所提高。在网络总效益和平均网络总效益仿真得出可得,该算法是可用于认知无线电频谱分配,在总体性能上改进型萤火虫算法优于基本萤火虫算法,因此达到寻求频谱分配更优目的。
[1] Xie Y P,Tan X Z,Ma L.A new algorithm for joint spectrum allocation in cognitive radio system[J].Journal of Harbin institute of technology university,2013,45(7):35-41.
[2] 杨淼,安建平.认知无线网络中一种基于蚁群优化的频谱分配算法[J].电子与信息学报,2011,33(10):2306-2311.
[3] 徐嵩,李玉峰.最大效益准则下基于分配公平性的CSGC改进算法[J].电子设计工程,2017,25(5):97-102.
[4] Krishnanand K N,Ghose D.Glowworm Swarm Optimization:a new method for optimizing multimodal functions[J].International Journal of Computational Intelligence Studies,2009,1(1):93-119.
[5] 吴斌,钱存华,倪卫红.萤火虫群优化算法在越库调度问题中的应用[J].计算机工程与应用,2013,49(6):39-42.
[6] 刘洲洲,王福豹,张克旺.基于改进萤火虫优化算法的WSN覆盖优化分析[J].传感技术学报,2013,26(5):675-682.
[7] 唐少虎,刘小明.一种改进的自适应步长的人工萤火虫算法[J].智能系统学报,2015,10(3):470-475.
[8] 顾忠伟,徐福缘.一种新颖的萤火虫算法求解PID控制器参数自整定问题[J].系统管理学报,2017,26(1):101-107.
[9] 姚洪曼,秦亮曦,胡盼.基于改进搜索策略和混沌机制的人工蜂群算法[J].计算机与现代化,2016(6):79-84.
[10] 杨迪雄,李刚,程耿东.非线性函数的混沌优化方法比较研究[J].计算力学学报,2004,21(3):257-262.
[11] 何利,郑湘渝,刘振坤.基于图着色理论的最大效用频谱分配算法[J].计算机工程,2011,37(19):93-95.
[12] 刘俊霞,卞琛.基于并行分配算法的认知无线电频谱分配算法[J].信息技术,2017(3):23-25.
[13] Solis F J,Wets R J B.Minimization by Random Search Techniques[J].Mathematics of Operations Research,1981,6:19-30.

