基于CCD的组合式测量系统研究

苏志部 ，邱丽梅 ，熊昌炯 ，艾子健

（1.三明学院 机电工程学院，福建 三明，365004；2.三明机械CAD工程研究中心，福建 三明，365004）

目前，常用的复杂曲面特别是大尺寸测量方法有室内GPS、激光跟踪仪，此类测量方法是先测量曲面上的特征点，再通过特征点坐标拟合出曲面[1-2]。虽然特征点的精度比较高，但是特征点数量拟合出曲面误差比较大，特别是曲面形状不规则的误差更大，且此类大型仪器对操作技术要求较高，设备安装较难，不宜推广[1-6]。

针对传统的大尺寸测量弊端，提出一种基于CCD的组合式测量系统，该系统由CCD定位系统、带有特征点的终端扫描系统和数据处理工作站组成。CCD系统将通过特征点来实现对终端扫描系统的各种姿态定位，然后定位信息提取各视角间的三维坐标转换参数从而得到多视角间点云数据的自动拼合。

1 基于CCD的组合式测量原理

1.1 基于CCD的空间定位原理

利用双目视觉定位原理进行定位，即小孔成像模型。由于小孔成像模型是理想模型，实际过程采集得到的图像往往会发生较大的径向畸变，所以不能利用简单的小孔成像模型，而是要建立一种具有误差补偿的基于一阶径向畸变模型[1-6]。其定位原理是把两幅以上的摄像机图像共同特征点在已标定模型中进行匹配并计算出相应的坐标。因此，影响双目定位系统的主要因素包括一阶畸变数学模型的误差补偿、摄像头图像质量和标定精度。

利用两个以上CCD的小孔成像模型，提取共同特征点的三维坐标，实现对特征点定位。由多个CCD构成的定位系统，关键是多个坐标系统的转换，包括了CCD自身坐标系（以下称CCD坐标系）、图像坐标系、世界坐标系，其中图像坐标系是二维的笛卡尔坐标系，包括了图像像素坐标系（u,v）和图像物理坐标系（X,Y），见图1。

图1 CCD小孔成像原理

现先定义CCD坐标系0XYZ与世界坐标系0XWYWZW的转换关系（R,T），其中，R表示旋转参数，T表示平移参数，可存在：

从图1孔成像模型可知，摄像机坐标与成像坐标（x，y）存在如下关系：

而且，成像坐标与像素坐标（u，v）存在关系是：

公式中的Sx、Sy分别表示图像X轴、Y轴方向的比例，且（U0,V0）代表CCD光轴与图像平面的交点，也是图像中心坐标。

综合以上可知世界坐标系与像素坐标存在如下关系：

因为系统零件包括光学元件在实际的加工、安装过程中、不可避免存在各种误差，采集得到的图像也会发生相应的畸变，按照方向可分为径向畸变和切向畸变，其中切向畸变对图像整体的影响非常小，所以本系统只考虑了径向畸变[4]，而摄像头本身存在不同位置的曲率是不一样的，这是引起径向畸变的主要原因。现以光轴为对称中心，可将畸变可分为：枕形畸变（正向）和桶形畸变（负向）[1-6]。但是畸变越多，所需畸变补偿系数就越多，这会增加模型的不确定性，所以本研究的定位系统模型只增加径向畸变补偿系数，建立基于一阶径向畸变模型其示意图2所示。

图2 基于一阶径向畸变模型

如果采集得到的图像发生畸变，这就需要在计算图像成像坐标与像素坐标的转换关系时需要进行畸变补偿，建立更加合理的畸变模型：

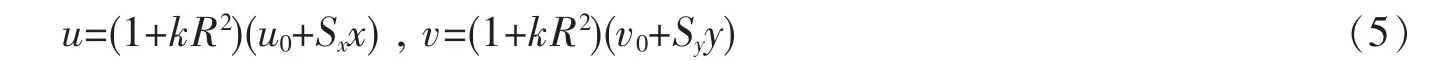
其中k为径向畸变系数、R为畸变半径[6]。

在测量系统中，主要依靠双CCD对终端扫描仪姿态的实时定位来计算转换系数的，所以双CCD定位系统自身标定也是本系统的重要环节，直接决定后续的定位精度。基于一阶径向畸变模型包括两类参数：外部参数和内部参数，其中内部参数主要是摄像机自身特性，包括焦距f、加工装配等引起的畸变系数k、系统比例Sx；外部参数是指CCD内部坐标系与外界（世界坐标系）建立起转换关系（包括3个旋转系数、3个平移系数），其他均为已知参数。 双CCD定位系统标定就是通过采集若干组带有约束特征的标定块或标定靶的图像，利用图像上的特征约束关系建立方程组，然后由方程组去计算畸变模型的外部参数和内部参数，标定块或是标定靶的约束特征决定系统标定效果。目前标定块没用统一的标准，常用的标定块约束特征有正方形、长方形、长方体等。本文采用的约束特征是个圆孔，因为通过精确提起圆孔边缘，可以比较容易拟合出圆心，如图3所示。

图3 9×11圆孔的标定块

1.2 多视角点云数据的自动拼合原理

基于CCD的组合式大尺寸三维测量系统如图4所示，主要是由多个CCD与便携式扫描仪组成。便携式扫描仪上布置3个以上的特征点，并在空间多个角度布置至少两个以上CCD摄像头，根据CCD的空间定位原理可知，CCD的数目越多其定位精度越高。CCD将会把同时采集的图像传送到计算主机，主机通过提取便携式扫描仪上的特征点来计算出此时测量仪的姿态。此处，可设CCD标定的坐标系为全局坐标系，其主要是通过测量便携式扫描仪的特征点全局坐标实现对其进行定位；设便携式扫描仪自标定的坐标系为局部坐标系，其主要是测量被测物体的各视点的点云数据[6-12]。 如果，测量时能将各视点的点云数据实时的转换到全局坐标系下，便能实现实时、高效的数据拼合。所以，通过特征点来计算出终端便携式扫描仪的空中姿态，从而计算出各视点的局部坐标系与全局坐标系的转换关系，包括旋转矩阵与平移矩阵，是多片数据自动拼合的关键环节。

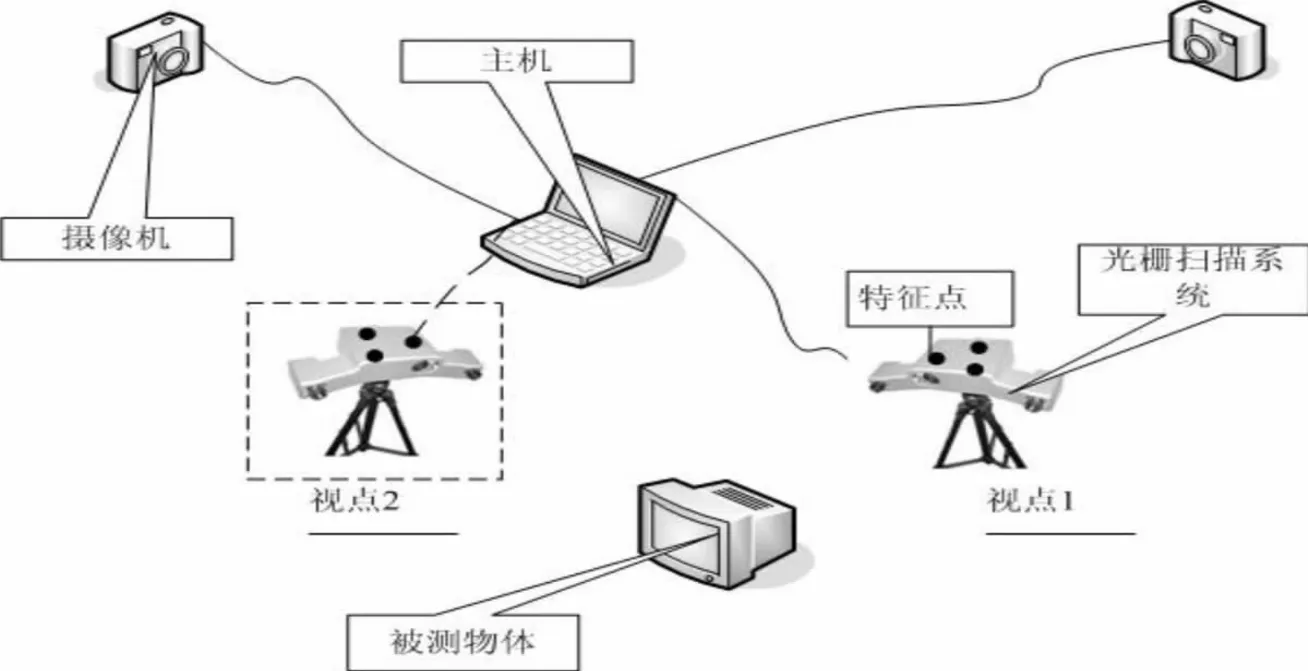
图4 基于CCD的组合式测量系统

本文在便携式扫描仪上粘贴3个特征点P1、P2、P3,通过P1、P2、P3建立局部坐标系。在局部坐标系中，P1为原点，P1P2方向为X轴；Y轴在平面△P1P2P3里垂直于X轴；在垂直于平面△P1P2P3方向为 Z 轴，假设特征点 P1、P2、P3 的局部坐标分别是 P1(x1，y1，z1)T、P2(x2，y2，z2)T、P3(x3，y3，z3)T，由局部坐标系的建立可知[6-11]：

利用双摄像机就可对特征点进行定位，并计算得到其全局坐标Q1T、Q2T、Q3T，假设局部坐标系与全局坐标系的旋转矩阵为R2，平移矩阵为T2，则：

由上式（7）可进一步计算得出：

公式中：

由于全局坐标系是由双CCD定位确定的，扫描得到的点云数据最后全部需要转换成全局坐标系下，才能实现自动拼合和测量，而局部坐标系是由特征点建立在便携式扫描仪上的坐标系，所以，若便携式扫描仪发生位置变动和姿态变化（如从视点1移到视点2），它们的转换参数也发生相应变化。

2 实验与分析

根据上述原理，需要对CCD组成的全局定位坐标系统结构参数进行标定和计算特征点组成的局部坐标系，及最终的点云自动拼合。本实验采用的设备包括：(1)由双CCD构建的空间定位系统；(2)便携式扫描仪：华中科技大学研发的PowerRE系统结构光三维扫描系统。

2.1 全局坐标系统标定实验

全局坐标系统标定实验是利用便携式扫描仪上的特征点来计算全局坐标系与局部坐标系的转换参数。根据双目视觉定位原理可知特征点至少要3个以上，才能解出方程，且特征点的分布要符合以下特征：a、所有特征点要分布在双CCD的视场下，才能对便携式扫描仪进行定位；b、特征点的分布要尽可能增大便携式扫描仪的移动范围，使其从多角度进行扫描。本实验采集单个视点标定图，如图5。

图5 双CCD采集的特征点标定图

经过标定匹配后可计算得到3个特征点的全局坐标系，见表1。

表1 特征点的全局坐标

由公式（7）、（8），可矩阵奇异值分解法计算出旋转矩阵 R2、平移矩阵 T2：

2.2 点云数据自动拼合实验

在本实验中，便携式扫描仪分别从3个不同的视点对观音工艺品进行拍摄，同时双目立体视觉系统对粘贴在其上的3个特征点进行追踪，根据上述标定的3个标志点在便携式扫描仪的局部坐标，计算每个视点下局部坐标系与全局坐标系的旋转、平移矩阵，完成数据自动拼合，各视点的点云数据如图6。

图6 各视点扫描得到的点云数据

经过计算转换成全局坐标系后自动拼合，效果如图7。

2.3 实验与性能分析

通过现有条件来标定基于CCD的组合式测量系统参数并完成多视点的点云数据自动拼合，证明该测量方法的正确性和可行性。本实验充分考虑了CCD的畸变因素进行误差补偿，并采集了多个特征点后进行奇异值分解法计算得到三坐标值，保证了标定方法的可靠性同时也进一步提高测量精度。跟其他传统的三坐标测量系统相比较，基于CCD的组合式测量系统采用常见的CCD图像传感元件，性价比高、安装方便、容易携带，同时也是一种非接触式测量，其测量范围大，不会受限于导轨和工作台等；也不同于当前市场上的激光跟踪仪、经纬仪测量系统等，基于CCD的组合式测量系统具有测量时间短、结构简单灵活、使用测量环境广、性能价格比高，并且随着CCD数量的扩充，测量精度将会进一步提高。

图7 点云数据拼合结果

3 结语

针对复杂曲面的工件三维点云数据量大且拼合难的问题，提出了一种基于CCD的组合式测量方法。该方法将便携式扫描仪的高精度测量和CCD空间定位方法相结合，从而达到复杂曲面或大尺寸工件的多视点点云数据自动拼合。 从上述测量实验可见，利用本文提出的基于双CCD的组合式测量系统，能够完成复杂曲面的多视点自动测量，并可实现点云拼合，极大地提高了测量效率，完全可以通过扩充CCD数量来完成大尺寸复杂曲面的测量。本文提出的组合式测量系统并没有完全将各种实际因素考虑进去，因此也存在一定误差，在以后的研究中将考虑更多的人为因素和算法自身局限性。

参考文献：

［1］陆峰，李宁，赵德宏.复杂曲面三维轮廓精度数字化比对检测与误差分析［J］.制造业自动化，2014，18：46－50.

［2］孙殿柱，史阳，刘华东，等.基于遗传算法的散乱点云最小包围盒求解［J］.北京航空航天大学学报，2013（8）：995－998.

［3］GENG L，ZHU J G，XIONG Z.Research on angle measurement uncertainty of wMPS［J］.Opto－Electronics Engineering，2011，38（10）：6－11。

［4］张晧琳，林嘉睿，邾继贵.三维坐标转换及其影响因素的研究［J］.光电工程，2012，2（30）：28－31.

［5］YING X，PENG K，HOU Y，et al.Self-calibration of catadioptric camera with two planar mirrors from silhouettes.［J］.IEEE Transactions on Pattern Analysis＆ Machine Intelligence， 2013，35（5）：1206－1220.

［6］苏志部.大尺寸测量的点云自动拼合技术研究［D］.武汉：华中科技大学，2009.

［7］刘慧强，陈文静，苏显渝，等.采用双频光栅投影的快速傅里叶变换轮廓术［J］.光电工程，2004，10（31）：39－42

［8］雷志辉，李健兵.基于双频投影条纹的全自动相位解包裹方法［J］.光学学报，2006，1（26）：39－42.

［9］WILLIAM W M.Two dimensional fringe pattern analysis［J］.Appl Opt，1983，22（23）：3898－3901.

［10］CATHERINE E，TOWERS，DAVID P T， JULIAN D C，et al.Time efficient Chinese remainder theorem algorithm for full field fringe phase analysis in multi－wavelength interferometry［J］.Opt Exp，2004，12（6）：1136－1147

［11］GHIGLIA D C，PRITT M D.Two－dimensional phase unwrapping：theory，algorithms，and software［M］.John Wiley and Sons，Inc，1998.

［12］潘伟.反向工程中光栅投影测量系统关键技术的研究［D］.上海：上海交通大学，2004.