石灰行业清洁生产等级评价方法及应用分析

王通华，李 强,2,3，李奇勇 ,2,3，王丽琴 ，邹晓玲

（1.三明学院 资源与化工学院福建，福建 三明 365004；2.福建省资源环境监测与可持续经营利用重点实验室，福建 三明 365004；3.清洁生产技术福建省高校工程研究中心，福建 三明 365004）

石灰是一种重要的工业原料，被广泛应用于建筑、冶金、化工等领域。石灰的生产是一个高能量耗散、高二氧化碳排放的过程，而目前我国石灰生产企业的技术水平参差不齐、工艺过程控制较为粗放、产品质量普遍不高，与当前世界上先进的石灰生产技术相比，在能源消耗、资源利用率和环境保护等方面仍然存在较大的差异[1-2]。为使石灰生产达到“节能、减排、降耗”的目的，实现石灰行业的可持续发展，必须对石灰生产企业进行清洁生产审核。因此需要建立石灰行业清洁生产评价指标体系，并确定合理的清洁生产等级评价方法，使企业明确其清洁生产的总体水平、找出存在的问题并发现其清洁生产潜能，以此促进石灰企业推进清洁生产。

1 石灰行业清洁生产评价指标体系的建立

1.1 构建清洁生产评价指标体系框架

为了使石灰行业的发展达到环保、节能和可持续发展的目标，根据《清洁生产评价指标体系编制通则》并结合石灰生产企业的实际情况，建立石灰行业清洁生产评价指标体系[3-5]，该体系包含7个一级指标和37个二级指标，具体清洁生产评价指标如表1所示。表1中“-”表示二级评价指标的政策或技术符合《工业清洁生产评价指标体系编制通则》；（*）内数字为石灰行业各评价指标的权重值；a、b、c分别表示石灰企业的二级评价指标满足Ⅰ、Ⅱ、Ⅲ级基准值。

表1 石灰行业清洁生产评价指标体系及3家石灰企业生产指标水平

1.2 确定清洁生产评价指标体系权重值

根据石灰行业的实际生产情况，采用层次分析法（AHP法）对构建的清洁生产评价指标体系框架中各同级指标相对重要性进行分析检验，以此确定各一级与二级指标的权重值。经过分析计算，各指标权重值见表1（表1中各一级与二级指标后面括号内的数字即为对应指标的权重值），构建及计算出的一、二级指标的判断矩阵、权重及其一致性比率分别如表2～9所示。

表2 一级指标评价指标判断矩阵及权重

表3 节能减排装备技术指标判断矩阵及权重

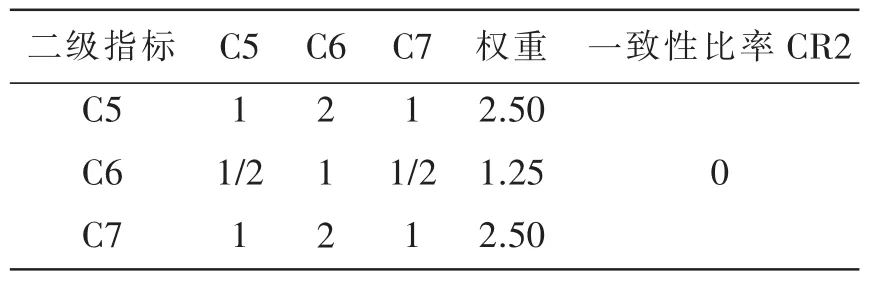
表4 产品特征指标判断矩阵及权重

表5 清洁生产管理指标判断矩阵及权重

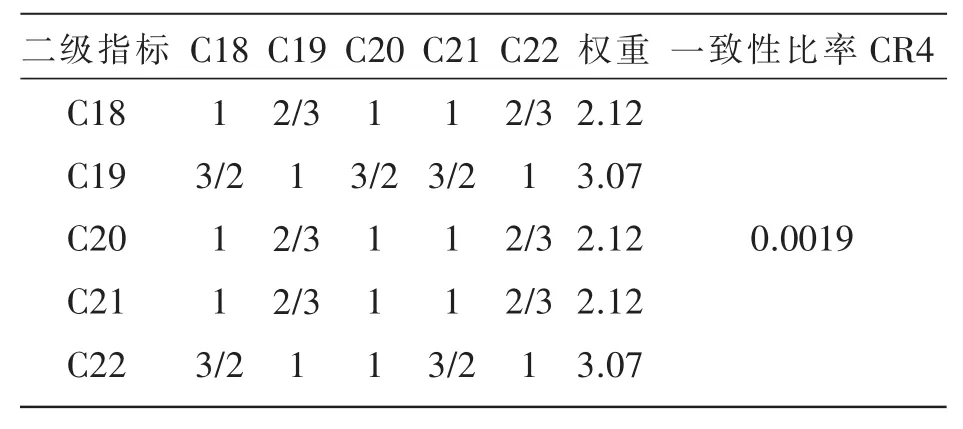
表6 资源综合利用指标判断矩阵及权重

表7 污染物排放控制指标判断矩阵及权重

表8 资源能源消耗指标判断矩阵及权重

表9 生产工艺装备及技术指标判断矩阵及权重

一级指标与二级指标的一致性比率分别为CR=0.0002、CR1=0.0029、CR2=0、CR3=0.0020、CR4=0.0019、CR5=0.0068、CR6=0、CR7=0.0007，其 CR值均小于0.1，所以指标判断矩阵都有很好的一致性，各指标之间选取的重要性标度是可以接受的，通过各判断矩阵计算出来的权重值可以作为实际评价的权重。

1.3 清洁生产评价指标的等级划分

用 Mk（k=1,2,3）表示第 k 个清洁生产等级，且规定 M1＞M2＞M3，即：Mk清洁生产效果比 Mk+1的清洁生产效果更佳。依据石灰行业的节能减排装备技术、产品特征、清洁生产管理、资源综合利用、污染物排放控制、资源能源消耗及生产工艺装备及技术等各种指标情况，将评价指标分为3个等级。其中M1表示国际清洁生产先进水平；M2表示国内清洁生产先进水平；M3表示国内清洁生产一般水平。

1.4 清洁生产评价指标隶属函数的确定

1.4.1 定性指标隶属函数

定性指标是对某些不易量化的工艺技术指标做定性评价，其隶属函数如式（1）所示。

式中：σijk表示的是：第i个的一级指标下第j个的二级指标隶属于Mk级的程度。

1.4.2 定量指标隶属函数

定量指标是对能够定量描述的某些设备配置或产品评价指标等进行定量评价。对于效益型指标，若实际值越大，其清洁生产等级越高，对应定量指标的隶属函数表示为式（2）～（4）所示，效益型指标隶属函数如图1所示。

图1 效益型指标隶属函数

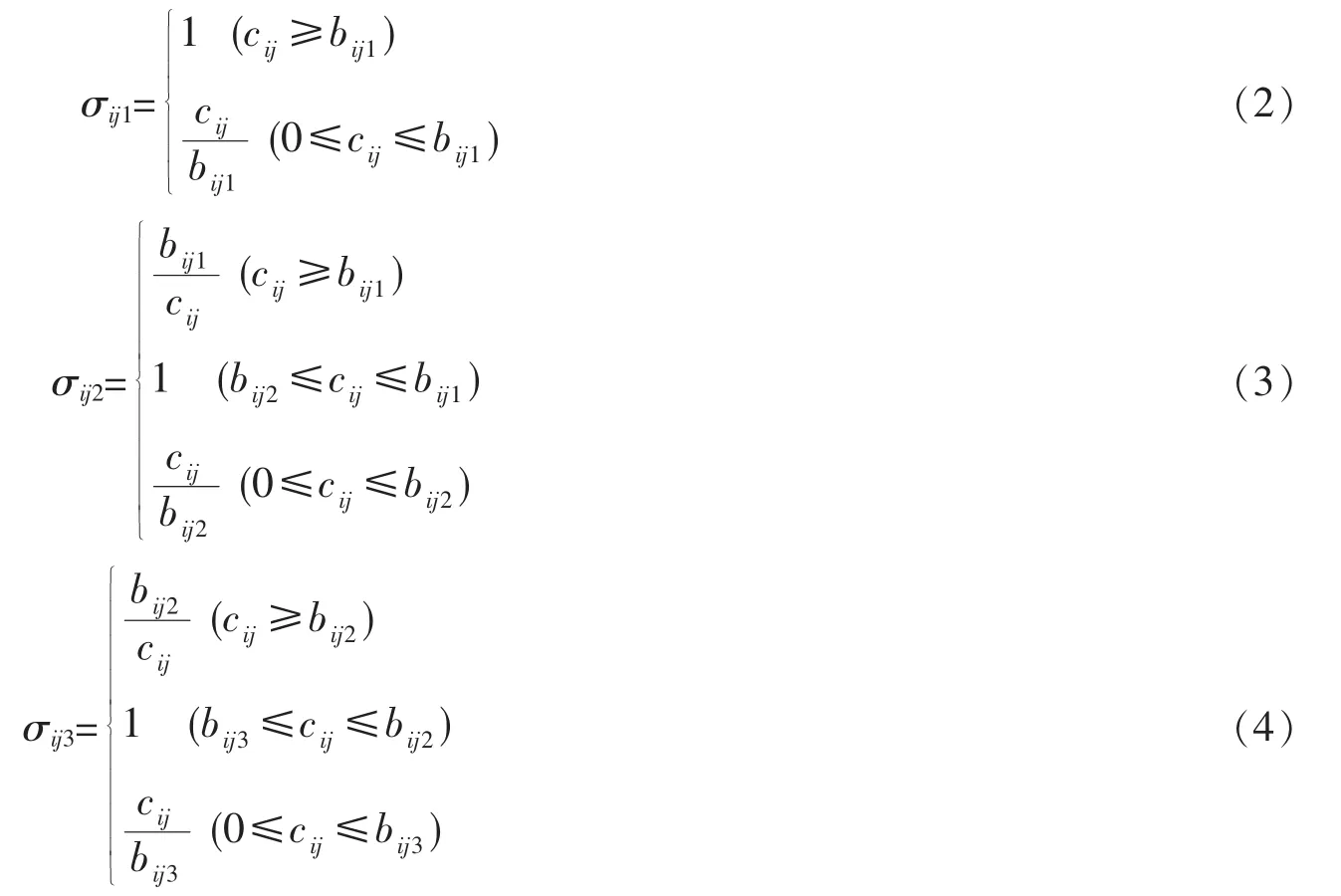
对成本型指标，若实际值越小，其清洁生产等级越高，对应定量指标的隶属函数可表示为式（5）～（7）所示，成本型指标隶属函数如图2所示

图2 成本型指标隶属函数

其中，cij表示的是石灰企业中第i个的一级指标下第j个的二级评价指标实际值；bijk表示的是石灰行业清洁生产指标中第i个的一级指标下第j个的二级评价指标等级为Mk的基准值。

当定量指标的3个级别的基准值均相同时，采用的隶属函数如式（8）所示：

2 基于两级模糊综合评判模型的石灰行业清洁生产等级评价与实例分析

2.1 清洁生产等级评价模糊数学评价方法

两级模糊综合评判模型是对受各指标制约的工艺过程做一个整体性的评价，该方法能解决未给出确切定量、不易量化的问题[6-8]。采用此模型对企业进行清洁生产等级评价，具有计算简便、结论清晰明了的特点，其具体的计算方式如下：

第一步，根据隶属函数式（1）～（8）和表1中的二级指标权重值以及石灰企业实际值计算得到二级模糊评价矩阵如下：

另设Ki为二级指标评价权重值，将其归一化得到权向量则系统二级综合模糊评价模式为：

第二步，根据第一步计算出的结果，建立一级模糊评价矩阵，得到一级模糊综合评价模式为：

其中，K为一级指标权重；Ai为第一步得到的二级模糊矩阵；ηi为一级模糊综合评价矩阵。

第三步，将一级模糊综合评判结果即综合隶属度向量归一化，对三家石灰行业做出等级评价。

2.2 基于两级模糊综合评判模型的石灰行业清洁生产等级评价实例分析

2.2.1 建立二级模糊综合评判

将某地区3家石灰企业A、B和C作为等级评价的研究对象，此3家石灰企业的生产规模及技术水平均处于行业中等水平左右，能够代表目前大部分的石灰企业在行业内所处的清洁生产水平情况，其清洁生产指标水平见表1。根据式（1）～（8）和表1计算石灰企业A关于二级评价指标的模糊评价矩阵，结果如下：

K1=（0.20,0.20,0.40,0.20）；K2=（0.40,0.20,0.40）；

K3=（0.17,0.09,0.17,0.17,0.05,0.09,0.09,0.05,0.09,0.05）；

K4=（0.17,0.25,0.17，0.17,0.25）；K5=（0.14,0.14,0.29,0.14,0.29）；

K6=（0.25,0.25,0.25,0.12,0.12）；K7=（0.20,0.30,0.10,0.20,0.20）。

通过公式Ai=Ki·Ri得到的系统二级模糊综合评价为：

A1=（0.64,0.58,0.74）；A2=（0.85,1.00,0.97）；A3=（0.97,0.42,0.39）；A4=（0.90,0.94,0.97）；

A5=（0.77,0.72,0.58）；A6=（0.84,0.98,0.80）；A7=（0.60,0.20,0.20）。

2.2.2 建立一级模糊综合评判

将上述计算获得的系统二级模糊综合评价结果作为一级评判矩阵，构成矩阵为：

一级指标权重值为 K=（0.1250,0.0625,0.1250,0.1205,0.1250,0.1875,0.2500），利用公式 ηi=K·Ai，计算得出A石灰企业的清洁生产等级的第一级模糊综合评判结果为：η1=（0.77，0.63，0.60）。同理可得：B、C 石灰企业的一级模糊综合评判结果为：η2=（0.62，0.65，0.73），η3=（0.59，0.80，0.62）。

用 Vi（i=1,2,3）表示 3家石灰企业，用 θi（i=1,2,3）表示3家石灰企业关于清洁生产等级Mk（k=1,2,3）的综合隶属度向量，如下：

θ1=（0.77，0.63，0.60），θ2=（0.62，0.65，0.73），θ3=（0.59，0.80，0.62）。

2.2.3 评价结果解析

将上述计算结果，即清洁生产等级的综合隶属度向量归一化后：

θ1=（0.39，0.32，0.30），θ2=（0.31，0.32，0.37），θ3=（0.29，0.40，0.31）。

若采用目前经常使用的最大隶属度原则来评价这3家石灰企业的清洁生产等级，可以得到如下结论：A石灰企业属于国际清洁生产先进水平 （即M1）；B石灰企业属于国内清洁生产一般水平（即M3）；C石灰企业属于国内清洁生产先进水平（即M2）。

从上述结论可以看出，依据最大隶属度原则，A石灰企业的清洁生产等级为M1，但其属于M1，M2，M3的隶属度相差很小，并且属于M2，M3的隶属度之和大于其属于M1的隶属度，即θ12+θ13=0.62>0.39=θ11。因此，在清洁生产等级评价中将A石灰企业评为M1是不恰当的，将其评为等级M2才更加切合A石灰企业的实际清洁生产水平。同理，将B石灰企业的清洁生产等级评价为M3也不够合理。导致企业清洁生产评价等级与其实际清洁生产水平不一致的主要原因在于最大隶属度原则主要考虑到的仅是隶属度在数值上的大小，而忽视了各个企业的清洁生产等级在位置上的差别。

3 基于二元语义的清洁生产等级评价分析

3.1 清洁生产等级评价的特征值法

为了更加准确、客观的对石灰企业清洁生产水平等级进行评价，引入级别特征值的概念：将清洁生产等级 Mk（k=1,2,3，…，λ）的级别变量定义为 k，同时把石灰企业 Vi（i=1,2,3，…，m）的级别特征值定义为式（11）：

由于 θik∈[0，1]和，于是有：

这表明ωi是一个无量纲的数量指标，数值处于清洁生产第1个等级（即M1）与第λ等级（即Mλ）水平两者之间，呈现了清洁生产等级评价综合隶属度与清洁生产等级2个方面的主要信息[9]。

用[ωi]=P 评定石灰企业 Vi（i=1,2,3，…，m）属于 P 级清洁生产水平（即 MP），其中[ωi]表示小于 ωi的最大整数，采取级别特征值的计算方式来评估石灰企业的清洁生产水平将比采用最大隶属度原则更加周全和接近实际情况。 在上述案例中，m=3，λ=3，根据公式（11）计算得：ω1=1.93、ω2=2.06、ω3=2.02。采用级别特征值方法，将A石灰企业评定为国际清洁生产先进水平（即M1），将B、C两家石灰企业评定为国内清洁生产先进水平（即M2）。

分析上述评定结果，可以发现ω1=1.93和ω2=2.06都与2很接近，显然这两者相差甚微，然而这两家石灰企业分别被评为M1和M2，评价结果不够合理。由于ω1=1.93和2很接近，理论上A石灰企业也应被评为M2，这种评定方法与采用最大隶属度原则来评定清洁生产等级相似，同样出现了不符合企业实际情况的问题。从以上两种方法可以看出，即使级别特征值法能更好的反映出石灰企业的整个清洁生产情况，但是它也存在一些不合理、不严谨的地方，并不能清楚的区分出各个石灰企业清洁生产水平的差异程度。

3.2 清洁生产等级评价的二元语义法

为避免出现上述不合理的问题，在评价过程中引入二元语义概念，建立石灰企业清洁生产等级评价的二元语义法。此方法不仅能切确评定企业的整体情况，又能正确的划分出各个企业的差异程度[10]。

若石灰企业Vi的级别特征值ωi满足：

则评定Vi的清洁生产等级为第P级（即MP）。为了确定石灰企业清洁生产等级水平属于P级的偏差程度，用偏差值表示为βiP=ωi-P，即-0.5≤βiP＜0.5。首先，将企业清洁生产等级评价的级别特征值用二元有序组表示（MP，βiP），其中 MP为清洁生产等级，βiP∈（-0.5，05）。

设（MP，βiP）和（M0，βjq）分别是石灰行业 Vi和 Vj（i，j=1,2,3，…，m）的级别特征值 ωi、ωj的二元语义，划定它的大小比较为：

若 MP＞Mq(P＜q)，则（MP，βiP）＞（M0，βjq），即 Vi的清洁生产等级高于 Vj；

若MP=Mq(P=q)，石灰企业Vi和Vj的清洁生产等级相同，则当：

(1)βiP=βjq时，（MP，βiP）=（M0，βjq），即 Vi和 Vj的清洁生产程度一样。

(2)βiP＞βjq时，（MP，βiP）＜（M0，βjq）时，即 Vi的清洁生产程度比 Vj差。

(3)βiP＜βjq时，（MP，βiP）＞（M0，βjq）时，，即 Vi的清洁生产程度比 Vj好。

依据式（12），石灰企业A、B和C的级别特征值的二元语义被表示为：ω1=(2,-0.07)，ω2=(2,0.06),ω3=(2,0.03)依据上述划定的二元语义的大小关系，可以将三家石灰企业的清洁生产等级均评定为M2（即国内清洁生产先进水平），但它们所处的清洁生产水平是不同的，其好坏排列顺序为：A＞C＞B，即A比较好，C居中，B较差。

将上述3家石灰企业的各二级指标实际值进行比较，可以发现A石灰企业各项指标实际值与B、C两家相比总体上更好，B石灰企业最差，经计算得到的优劣排序也与各石灰企业的实际情况一致。

4 结论

建立石灰行业清洁生产评价指标体系后，为评估各石灰企业的清洁生产等级水平，先后采用三种方法进行评价，最后根据评价结果的比较分析，得出如下结论：

(1）最大隶属度原则评价法：其清洁生产等级评价分别为：A石灰企业评为M1；B石灰企业评为M3；C石灰企业评为M2。评定结果与实际情况不相符。

(2）级别特征值评价法：其清洁生产等级评价分别为：A石灰企业评为M1；B、C石灰行业均评为M2。其评定结果也会呈现少许不符合企业整体清洁生产的情况。

(3）二元语义评价法：其清洁生产等级评价为：A、B、C石灰企业均评为M2，其清洁生产水平的差异排序为：A较好，B较差，C居中。评定结果与实际情况相符。

因此，清洁生产等级评价的二元语义法能够更直观的反应各企业的清洁生产情况，评定结果准确可靠，且能够划分出同一清洁生产等级下不同企业清洁生产水平的优劣情况。

参考文献：

［1］符敬慧.我国石灰行业发展现状及发展趋势分析［J］.建材发展导向，2014，12（20）：20－23.

［2］李银山.石灰竖窑设备安装及工艺生产的优化［J］.耐火与石灰，2017，42（4）：3－7.

［3］李奇勇，李强.不锈钢行业清洁生产评价指标体系研究及应用［J］.工业安全与环保，2017，43（1）：103－106.

［4］武祝民，于宏兵.危险废物处理处置企业清洁生产案例研究［J］.环境工程，2016（8）：170－173.

［5］周露，宋若阳，陈亢利.清洁生产评价指标体系组成与发展［J］.四川环境，2016，35（6）：157－162.

［6］孙根行，狄倩，杨帆，等.CASS工艺城市污水处理厂清洁生产评价指标体系的构建及应用［J］.陕西科技大学学报，2014，32（3）：30－34.

［7］汪利平，于秀玲，杨继东，等.AHP－模糊综合评价法在清洁生产审核中的应用研究［J］.环境科学与管理，2014，37（12）：180－188.

［8］杨圣春.多级模糊综合评价在火电厂清洁生产中的应用［J］.合肥工业大学学报（自然科学版），2011，34（9）：1408－1412.

［9］刘家财，李登峰.钢铁行业清洁生产等级评估模型与方法［J］.环境工程，2014（10）：113－118.

［10］王丽玲，张树深，张芸.城镇污水处理厂清洁生产等级评价二元语义模型与方法［J］.中国环境科学，2014，34（11）：2976-2984.