基于深度值和M-估计的人脸姿态估计
邱丽梅 ,邱思杰
(1.三明学院 机电工程学院,福建 三明,365004;2.机械现代设计制造技术福建省高校工程研究中心,福建 三明,365004)
近年来,虽然随着深度摄像机技术的发展及微软Kinect的问世,打破了以往深度摄像头高昂价格的局面,人脸姿态估计领域也出现了ETH Face Pose和 Biwi Kinect两个新的深度图像数据库[1],但在海关、机场、展览馆等公共场合及公安追捕罪犯系统等实际应用中,对于单幅二维人脸图像的多姿态识别仍居主流[2]。目前,正面人脸识别系统已取得了较好的识别效果,但是多姿态人脸图像的有效识别,效果仍然欠佳。据统计大约 75%的人脸图像为非正面的人脸图像[2],除此以外,人脸姿态还在智慧城市、司机疲劳检测系统和智能轮椅等方面都有着广泛的应用[3]。
根据实现原理和方式的不同,现有的人脸姿态估计方法大体上可以分为六类[4]:⑴形状模板匹配的方法[5-6];⑵检测分类器的方法[7-8];⑶特征回归的方法[9-10];⑷流形嵌入的方法[11-12];⑸局部约束模型的方法[13];⑹脸部特征点几何关系的方法[14-16]。其中,脸部特征点几何关系的方法具有简单、耗时短、效率高等优点,而且随着人脸特征点提取算法的日趋成熟,脸部关键特征点的检测和定位精度已逐渐获得保障[17]。
针对单幅人脸图像,依据以下几点:⑴多姿态二维人脸图像识别仍居主流;⑵脸部特征点几何关系方法具有简单、耗时短、效率高等优点;⑶现有的姿态估计方法大多存在缺乏人脸特征深度信息而造成姿态估计过程病态化的问题;⑷最小二乘法不能很好地区分内点和外点,提出了基于深度值和M-估计的人脸姿态估计方法。
1 求解人脸特征点的深度值
对于单幅人脸图像在不知道人脸特征点深度值及其它信息的前提下,只利用脸部特征点几何关系估计人脸空间姿态是不易实现的。若能得知人脸特征点的深度值,就能丰富人脸预知信息,精准实现对单张照片中人脸的姿态估计。
采用CMU PIE人脸图像为研究对象,进行了相关预处理后,得到大小为64×64的图像。先利用改进的活动形状模型(Active Shape Model,简称ASM)方法提取人脸特征点[17],再利用透视原理和迭代算法计算得到人脸特征点的深度值。
假设一特征点的3D空间坐标为yn=(yn1yn2yn3)T和相应的2D投影坐标为un=(un1un2)T,旋转矩阵 R=(r1,r2, r3)T,平移矢量 t=(t1,t2, t3)T,f为像机焦距,则:

在相机坐标系中,根据透视成像有:

yn经过旋转R,平移t后得到xn,则:
在相机坐标系中,假设xn的深度值为dn,n=1,2,3,Λ,N则:
(1)选取xn的初始深度值为是人脸特征点与透视中心的距离;

其中,ε2为方差,{wn|n=1,Λ,N}是非零因子,满足 wn>0,在此定义 wn相等且 wn=1/N。 Rk和 tk分别是第步时所对应的人脸旋转矩阵和平移矩阵,即人脸姿态值。


可见,要使式(5)取得最小值,那么:

此时,(5)式就变成了:


把式(3)代入(8)式,可得:

2 基于深度值和M-估计的人脸姿态估计
由于特征点提取误差不可避免的产生个别误差较大的外点,最小二乘法不能很好地区分内点和外点,从而影响估计精度和鲁棒性,因此,在最小二乘法的基础上,加入M-估计算法进一步优化。
随机的估计值Tk,可由下式最小化形式表示:

或可通过下列隐式方程表示:

其中,ρ是原函数:

把式(12)写成以下等式形式:

其中:

所以,Tk可以被表示成:

本文采用Huber的ρ和Ψ算子,表示如下:

a是调整常数,取残差绝对值的常数倍,在此处a=1.5。
非线性回归问题可以描述如下:
假设函数 fi:Em→E,i=1,2,3,Λ,n;θ=(θ1,θ2,Λ,θm)T∈Em是未知的 m 维向量,则:

求解方程式(18),即求解式(19)

有数种不同的方法,为了构造一种呈比例变化的M-估计,估计比例因子取值如下:

通过修正残差值的方法来解式(19)最小问题,确定θ的步骤如下:
(1) 选择初始的 θ0;
(2)假设第k步的迭代值是θk,则按以下步骤来解决:
(a)计算残差值 ri*,i=1,2,3,Λ,n,则:
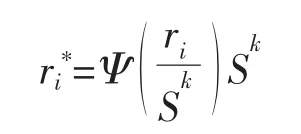
(b)求解最小二乘问题 Xδ=r*,其中,是梯度矩阵,即:

采用一般的最小二乘法便可求解此方程;如果采用奇异值分解法,则X=UΣVT,那么其解为=
(c)θk+1=θk+。
3 实验
3.1 实验步骤
本次实验在Matlab 2012a环境下编程所得,其实现步骤如图1所示。

图1 人脸姿态估计流程图
⑴输入待估计姿态人脸图像。
⑵把输入的彩色图像转化成灰度图像、灰度值归一化为[0,1],并进行去噪和标准化处理,图像大小统一处理为64×64。
⑶对处理好的人脸图像,引入仿射变换不变性初始化原则(ATIIA)建立初始模型,改进传统的活动形状模型(ASM)方法[17],提取左右眼内外角点、左右嘴角点、鼻尖点、两鼻翼点和下巴顶点等共十个主要人脸特征点的二维值。
⑷根据透视成像原理,利用迭代算法,求得特征点的深度值。
⑸选用左右眼内外角点、左右嘴角点、鼻尖点、两鼻翼点和下巴顶点等共十个主要特征点来表示人脸,利用透视成像原理,建立人脸姿态估计目标函数。
⑹利用两外眼点、鼻下点和嘴角点等四个特征点进行姿态一次估计,作为对目标函数进行最小二乘优化运算的输入值,输出二次估计的姿态结果,并把它们作为下步M-估计的初始值。
⑺利用M-估计算法对最小二乘法得到的估计值作进一步优化,输出最终估计结果。
3.2 实验数据
实验采用CMU PIE人脸数据库,该数据库包含了68个人的人脸,均为彩色图像,以PPM格式存储,分辨率为640×486,人脸图像大小不一,背景多样,4种不同表情,43种不同光照,13个离散姿态,共41368幅人脸图像。
实验前,我们把彩色图像转化成灰度图像、灰度值归一化为[0,1],并进行去噪和标准化处理,图像大小统一处理为 64×64。 对其中的 β=0°,±22.5°,±45°5个姿态共 170幅人脸图像进行了测试,其中也包含了部分“自遮挡”(眼镜和少量头发遮挡)。随机选取了部分实验图像,如图2所示。
3.3 实验结果与分析
一般的应用系统中,对绕Y轴旋转(β)的侧面图像应用较多,因此,随机选取部分真值为β=0°,±22.5°,±45°这5种姿态图像,如图3所示。图中第一组数据为本文算法(最小二乘法+M-估计优化算法)估计得出的姿态值,第二组数据为最小二乘算法估计得出的姿态值,结果表示形式为(α,β,γ),单位为度(°),随机选取部分测试结果如图3所示。

图2 部分预处理后的实验图像

图3 部分估计结果
对于人脸姿态估计的性能评价指标通常有:平均绝对误差、绝对误差标准差和方向估计精度3种[4],平均绝对误差是估计精度最为简单的评价指标,也是估计系统通用的指标,一般误差在5°以内,认为是有效估计。表1中分别给出了本文算法和最小二乘法的β平均绝对误差。

表1 β的平均绝对误差对比表
通过对比图3和表1可以发现:两种算法的姿态估计误差随着角度的增加而增大,其中真值为β=0°,±22.5°时,两种算法估计误差相差不大,都控制在 3°内的高精度估计;真值为 β=±45°的情况下,本文算法误差仍稳定地控制在3°内的高精度,而最小二乘算法则出现了不稳定现象,误差时而在3°以内,时而超过4°,但平均绝对误差也都控制在5°以内的有效估计。
4 结论
本文提出的基于深度值的单幅图像人脸姿态估计方法,利用了透视原理和迭代算法计算出特征点的深度值,克服了现有姿态估计方法大多存在缺乏人脸特征深度信息而造成姿态估计过程病态化的缺陷;利用M-估计算法解决了最小二乘法不能很好地区分内点和外点的问题,保证了估计精度和鲁棒性。通过CMU PIE人脸数据库进行实验,结果表明:对于β=-45°~+45°的单幅二维人脸图像,本算法具有良好的估计精度和鲁棒性。
参考文献:
[1]JOHN DARBY,MARI'A B SA'NCHEZ,PENELOPE B.BUTLER,et al.An evaluation of 3D head pose estimation using the Microsoft Kinect V2[J].Gait Posture,2016,48(4):83-88.
[2]马丙鹏,山世光,陈熙霖,等.一种基于图像表观的鲁棒姿态估计方法[J].软件学报,2009,20(6):1651-1663.
[3]WU SIYU,LIANG JIE,JASON HO.Head pose estimation and its application in TV viewers'behavior analysis[C]//Electrical and Computer Engineering.IEEE, 2016:1-6.
[4]唐云祁,孙哲南,谭铁牛.头部姿势估计研究综述[J].模式识别与人工智能,2014,27(3):213-225.
[5]PADELERIS P,ZABULIS X,ARGYROS A A.Head pose estimation on depth data based on particle swarm optimization [C]//Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.2012:42-49.
[6]NHAT QUAN,HUYNH NGUYEN,THAI HOANG LE.Pose estimation using local binary patterns for face recognition[C]//Springer International Publishing Switzerland 2015.
[7]ROBERTO VALLE,JOS′E MIGUEL BUENAPOSADA,ANTONIO VALDE′S,et al.Head-pose wstimation inthe-wild using a random forest[C]//Springer International Publishing Switzerland 2016.
[8]SRIJA CHOWDHURY,JAYA SIL.Head pose estimation for recognizing face images using collaborative representation based classification[C]//Proc of the Conference on Advances in Computing,Communications and Informatics (ICACCI),2016:571-575.
[9]FANELLI G,DANTONE M,GALL J,et al.Random forests for real time 3D face analysis[J].International Journal of Computer Vision,2013,101(3):437-458.
[10]MA B P,CHAI X J,WANG T J.A novel feature descriptor based on biologically inspired feature for head pose estimation[J].Neuro-computing,2013,115(4):1-10;
[11]LU J W,TAN Y P.Ordinary preserving manifold analysis for human age and head pose estimation[J].IEEE Trans on Human Machine Systems,2013,43(2):249-258.
[12]范进富,陈锻生.流形学习与非线性回归结合的头部姿态估计[J].中国图象图形学报,2012,17(8):1002-1010.
[13]ZHU X X,RAMANAN D.Face detection,pose estimation,and landmark localization in the wild[C]//Proc of the IEEE Conference on Computer Vision and Pattern Recognition,2012:2879-2886;
[14]HARI C V,PRAVEEN SANKARAN.A clustered locally linear approach on face manifolds for pose Estimation[C]//Springer Verlag London 2016.
[15]LIANG X N,TONG W Q.Face pose estimation using near-infrared images[C]//Proc of the International Conference on Communication Systems and Network Technologies,2012:216-220.
[16]ANWAR SAEED,AYOUB AL HAMADI,SEBASTIAN HANDRICH.Advancement in the head pose estimation via depth-based face spotting[C]//IEEE Symposium Series on Computational Intelligence,2016.
[17]WAN K W,LAM K M,CHONG K.An accurate active shape model for facial feature extraction[J].Pattern Recognition Letters,2005,26(12):2409-2423.

