能耗大数据P-规律及其生成

尤垂桔，邱锦明

（1.三明学院 信息工程学院，福建 三明 365004;2.数字福建工业能源大数据研究所，福建 三明 365004;3.工业大数据分析及应用福建省高校重点实验室，福建 三明 365004;4.物联网应用福建省高校工程研究中心，福建 三明 365004）

“十三五”期间，我国能源刚性需求增长，节能减排形势依然严峻。由于工业能源数据量大、实时性强、维数高、干扰大，工业能源大数据的用能优化面临挑战。因此，如何从工业能源大数据中发掘出能源的用能规律，用于企业能源管理决策，优化生产运行方式，提高能源利用效率和管理水平，是当前工业企业实施能源管理亟待解决的问题。

由于工业生产环境的复杂性，工业用能系统的用能过程往往受到如压力、温度、湿度、电压等多种因素的影响，使得能耗（能源消耗）大数据具有多源、多模态的动态性和不确定性。如果把影响设备的用能因素看作能耗因子（能耗属性）α，那么设备的用能过程就可抽象为能耗因子α通过迁移 f作用于用能系统A的过程，或者是能耗因子α对用能系统A的 f-属性入侵。显然，工业用能系统的能耗动态变化规律与能耗因子之间存在着某种关系，人们希望通过这个关系掌握工业用能系统的能耗与能耗因子之间的动态规律，为企业能源管理提供决策依据和技术支持。

设 U={u1(x),u2(x),…,un(x)}是用能系统的能耗规律（函数）集， α={α1,α2,…,αk}是 U 的能耗属性集，如果α受到 f-干扰变成αf，能耗规律集U变成Uf，或者对U的属性集α的 f干扰生成了能耗规律集Uf。显然U与Uf存在某种关系，这个过程等价于函数集合S的属性集α={α1,α2,…,αk}受到f干扰，使得S中的元素发生变化，生成S的函数内P集（集合中规律元素减少）或S的函数外P集合Sf（集合中规律元素增多），集合对,Sf)称为函数集合S生成的函数P-集合。函数P-集具有动态特征和规律特征，把这一特征与性质拓展应用到工业能源管理,那么能耗因子对用能系统的干预,等价于用能系统受到f-能耗属性的入侵，引起用能系统的能耗规律变化。自然产生以下几个问题：f-能耗属性入侵与用能系统的能耗变化之间存在什么关系?在f-能耗属性入侵作用下,用能系统的能耗变化是否存在规律?这样的关系和规律如果存在，能否被识别？

本文基于函数P-集，利用MapReduce研究能耗大数据环境下用能系统的能耗规律，对 f-能耗属性入侵与用能系统的能耗变化关系，在f-能耗属性入侵作用下的用能系统能耗变化规律和识别准则展开讨论。

1 能耗P-规律及其性质

1.1 函数P-集[1]简介

约定 U(x)是有限函数论域，F(α)是有限属性干扰论域，V(α) 是有限属性论域，S(x)={s(x)1，s(x)2，…，s(x)m}是 U(x)上的有限函数集，α={α1,α2,…,αk}是 V(α)上的有限属性集，f={f1，f2，…，fn}是 F(α)的干扰集，s(x)是 x 的函数。 为了简单且不引起误解，U(x)，V(α)，s(x)分别记作 U，V，s。

定义 1给定函数集 S={s1，s2，…，sq}⊂U， α={α1，α2，…，αk}⊂V 是 S 的属性集， f={f1，f2，…，fn}是α的干扰族。α在f干扰下变成αf，函数集S变成Sf¯，称Sf¯是S的属性集在f干扰下生成的函数内P-集合(function internal packet set)，而且

S-称作S的函数（元素）删除集合。 这里，αf⊇α，

定义 2给定函数集 S={s1，s2，…，sq}⊂U， α={α1，α2，…，αk}⊂V 是 S 的属性集，f={f1，f2，…，fn}是α的干扰族。α在干扰下变成函数集S变成，称Sf是S的属性集在干扰下生成的函数外 P-集合(function internal packet set)，而且

S+称作S的f-函数（元素）补充集合。这里，⊆α，Sf⊇S。

函数P-集的动态特征：函数P-集是以函数集合S为原点，由于函数集合S的属性集α受到内外部因素 f干扰，引起函数集合S的动态扩充和收缩。

1.2 能耗P-规律

约定 U是有限能耗规律（函数）论域，X⊂U是用能系统A的能耗规律（函数）集合,V是有限能耗因子（属性）论域，F 是能耗因子（属性）干扰论域，α={α1，α2，…，αm}⊂V 是 X 对应的能耗因子（属性）集,f={f1，f2，…，fn}⊂F 是能耗因子干扰族。

定义 1设 X={x1,x2,…,xk}⊆U 是能耗函数集，α={α1，α2，…，αm}是用能系统 A 的能耗因子集合，δ=[δi,δj]是用能系统A的能耗因子α在f干扰下的能耗区间，X是用能系统A在能耗区间δ上生成的能耗函数集，称能耗区间δ是X的能耗因子α在f干扰下的δ-稳定区间，记为。 这里， δi,δj表示用能系统的能耗常数,i＜j。

定义 2设X={x1,x2,…,xk}⊆U是能耗函数集，是用能系统 A 的 δ-稳定区间，称在内形成的能耗函数集[x]是U上的能耗函数稳定集合，记为

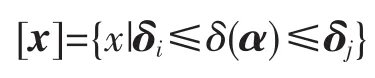
定义 3设f是能耗因子α对用能系统A的干扰，若在f干扰下，使得用能系统A的能耗稳定区间δ扩展为δ+，且δ⊆δ+，称f是对用能系统A的正干扰，记为f+；若在f干扰下，使得用能系统A的能耗稳定区间δ压缩为δ-，δ⊇δ-，称f是对用能系统A的f负干扰，记为f-。

定义 4设X={x1,x2,…,xk}⊆U是能耗函数集，δ+是用能系统A的能耗因子α在f+干扰下的能耗区间，称是X在δ+下生成的能耗函数外P集合。

定义 5设X={x1,x2,…,xk}⊆U是能耗函数集，δ-是用能系统A的能耗因子α在f-干扰下的能耗区间，称是X在δ-下生成的能耗函数内P集合。

定义 6由和构成的能耗函数集合对，称作能耗函数集合X生成的能耗函数P-集合，记为

定义 7给定在某一区间δ下能耗函数集合[x]={x1,x2,…,xm},是 xi∈[x]的离散数据分布，如果

这里 xi,k∈R，i=1,2,…,m；k=1,2,…,n，R 是实数集。

根据（2）式，利用

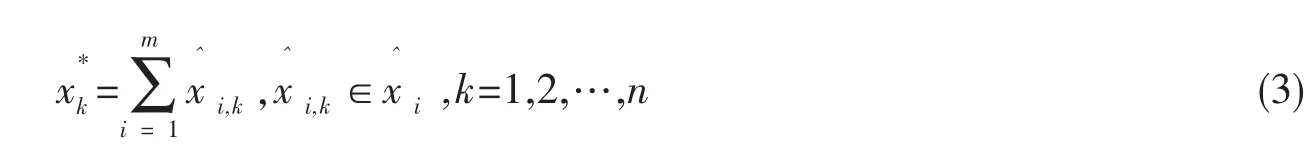
得到[x]的合成规律[x]*。给出[x]*离散数据分布的数据点形式：

根据（4），利用 Lagrange 插值，有

得到[x]*生成的多项式规律p(x)：

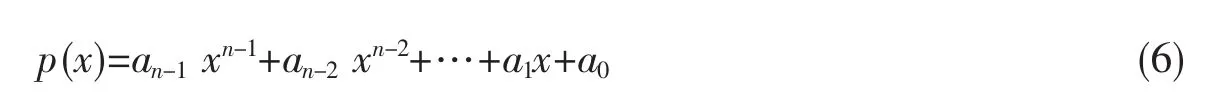
(6)式只是[x]*规律的生成形式之一，规律其它生成形式略。

定义 8称生成的δ+正干扰规律，如果

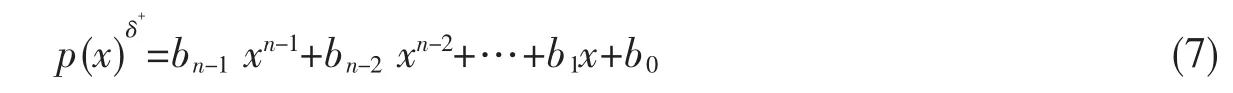
定义 9称生成的δ-负干扰规律，如果

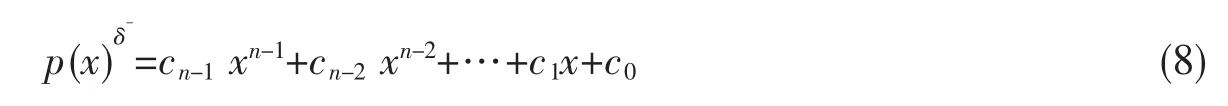
定义 10由构成的规律对，称为能耗函数P-集合生成的能耗P-规律，记为

定义11如果,则生成的规律形成一个能耗P-规律带，记为：

1.3 能耗P-规律的性质

命题1能耗P-规律存在且非唯一。

命题2能耗P-规律具有迁移特性。

定理1（能耗P-规律序定理） 设分别是用能系统A的能耗因子α在f+干扰下的能耗区间，分别是用能系统A的能耗因子α在f-干扰下的能耗区间，且分别是用能系统在能耗区间上生成的规律分别是用能系统在能耗区间上生成的规律，则：

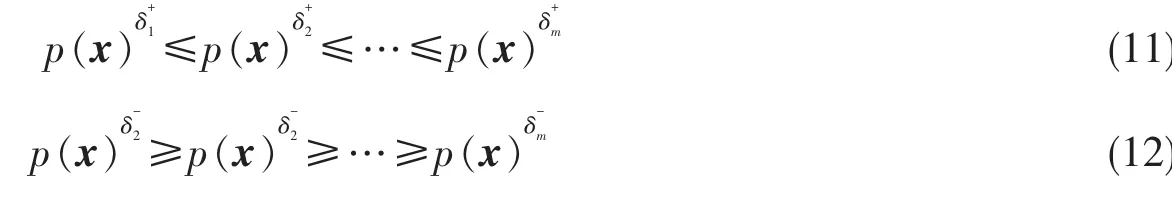
证明：设分别是上生成的能耗函数集，因为，根据定义4，得到：

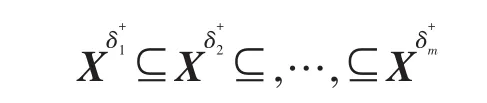
根据式（2）～（6），得到：

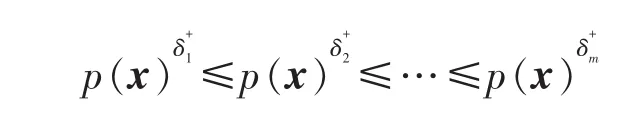
根据式（2）～（6），得到：

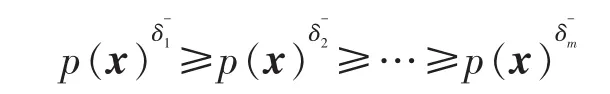
定理2（能耗P-规律带定理）如果用能系统A的能耗区间对应的能耗函数集，对应的能耗函数集，生成的规律，分别为生成的规律，则：

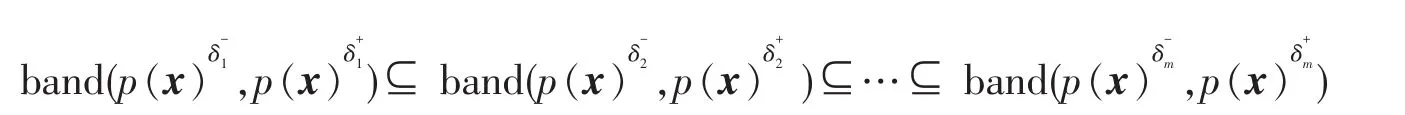
证明：因为根据定理1（能耗P-规律序定理），有

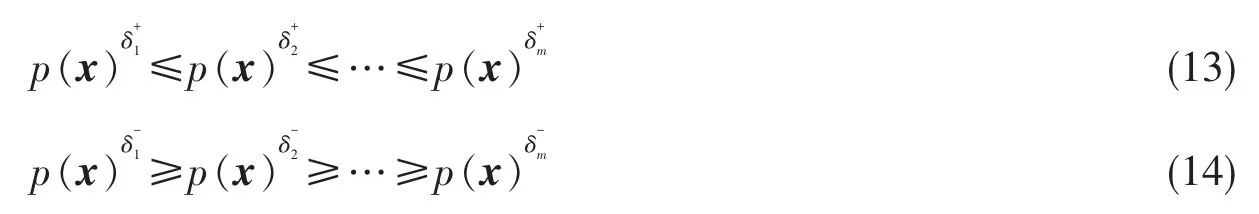
由(13)，(14)有：

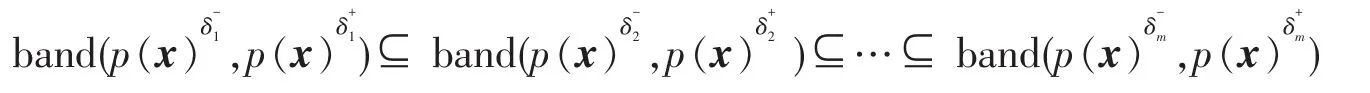
定理3（能耗P-规律 f干扰区间内稳定定理）设δfi，δfj分别是用能系统A的能耗因子α在 f干扰下的能耗区间，且δfi⊆δfj，如果用能系统A在区间δfi形成的规律稳定，那么用能系统A在区间δfj生成的规律在区间δfi上稳定。

证明：设为用能系统A在δfi区间上的能耗函数集，为用能系统A在δfj区间上的能耗函数集，为用能系统A 在上生成的规律，为用能系统A在上生成的规律，由于δfi⊆，根据定理 1（能耗 P-规律序定理）有因此用能系统A在区间δfi生成的规律在区间δfj上稳定。

定理4（能耗P-规律f-辨识定理）能耗P-规律可辨识的充分必要条件是用能系统A的能耗因子 α 在 f干扰下形成的能耗区间 δfi≠δfj，这里i≠j。

证明：设是用能系统A在区间δfi上生成的能耗规律，是用能系统A在δfj上生成的能耗规律，因为，那么必有 δfi⊂δfj或者 δfi⊃δfj，根据定理 1，有或者所以，即能耗规律是可辨识的。

2 能耗大数据P-规律生成算法

定义12设X={x1,x2,…,xk}⊆U是能耗数据（记录）集，为用能系统A的能耗因子α在f干扰下的能耗区间，称[x]i={xi,1,xi,2,…,xi,m}是X的关于的一个能耗数据（记录）稳定性划分。

定义13设X={x1,x2,…,xk}⊆U是能耗数据（记录）集为用能系统A的能耗因子α在f干扰下的能耗区间，[x]i={xi,1,xi,2,…,xi,m}是X的关于的一个能耗数据（记录）稳定性划分；为用能系统A的能耗因子α在f+干扰下的能耗区间，且是 X 关于的一个能耗数据（记录）扩展稳定性划分；为用能系统A的能耗因子α在f-干扰下的能耗区间，且是 X 关于的一个能耗数据（记录）压缩稳定性划分，在生成的规律记为，在生成的规律记为，[x]i生成的规律记为形成关于能耗规律P([x]i)的能耗P-规律。

能耗大数据P-规律生成过程如图1所示。

能耗大数据P-规律生成算法步骤如下：

（1）划分能耗大数据集 X 为 n 个子集 split(X,n)={[x]1,[x]2,…,[x]n}，X=[x]1∪[x]2∪…∪[x]n，[x]i∩[x]j=Φ,i≠j，且 1≤i＜j≤n。

（2）对每个能耗数据子集[x]i,i=1,2,…,n，对[x]i子集的每条能耗数据记录进行解析，形成key(能耗c)-value(能耗因子α)的键值对集合s([x]i)。

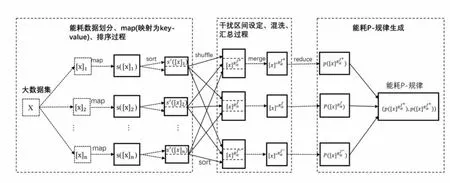
图1 能耗大数据P规律生成过程

（3）对（2）步产生的结果 s([x]i)，i=1,2,…,n，按照 key（能耗 c）进行排序，对相同的 key 进行归并，形成新的key(能耗c)-value(能耗因子α)的键值对集合s'([x]i),i=1,2,…,n。

（5）根据（3）的结果，对 s'([x]i),i=1,2,…,n中的每一个键值对记录，以 key（能耗 c）为依据，分别映射（shuffle）到按照（4）设定的能耗区间，形成3个新的key（能耗c能耗因子）-value（能耗因子α）键值对形式的数据集

（8）对（7）的结果，根据式（2）～（6），生成能耗规律

重复步骤（4）～（9），在步骤（4），可依据能耗因子α的f干扰程度，设定扩展能耗区间和压缩能耗区间，i=1,2,…,m，且满足，根据定理2（能耗P-规律带定理），将形成能耗P-规律带。

3 能耗大数据P-规律生成实验分析

本实验以工业锅炉为例研究工业锅炉的能效问题。抽取了某工业锅炉的能耗数据记录作为研究对象，实验中只考虑排烟温度（α1）、排烟处过量空气系数（α2）、排烟处 O2（α3）、给水温度（α4）等 4个能耗因子对热效率的影响。为了计算方便，在本实验中对能耗因子的影响数值进行归一规范化处理，控制在[0,1]之间。设定能耗区间，其扩展区间以及压缩区间且满足经过能耗大数据P-规律生成算法步骤(1)～(7)，分别得到在能耗区间对应的能耗函数集

表1 离散数据

表1 离散数据

xif1-yif2-yiyiff1+yif2+yi 0.15 1.8577 2.2662 2.4637 2.9215 3.3492 0.3 1.7380 2.1368 2.3581 2.7793 3.1482 0.45 1.6409 2.0159 2.2833 2.6710 2.9968 0.6 1.5665 1.9063 2.2392 2.5910 2.8951 0.75 1.5146 1.8149 2.2259 2.5322 2.8430 0.9 1.4853 1.7540 2.2433 2.4874 2.8407

由表 1 数据，利用（5）～（6）式，分别得到在能耗区间下对应的能耗规律

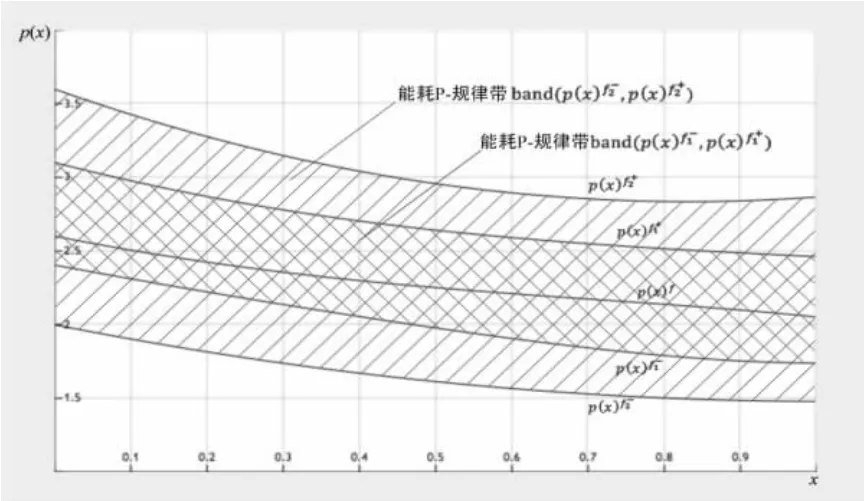
图2 能耗P-规律图

根据以上的实验分析过程，结合图2，可得如下结论：

(3)当用能系统的能耗因子受到环境因素的f干扰，引起能耗区间从迁移到迁移到导致能耗P-规律从迁移到，因此能耗P-规律具有迁移特性。

4 总结

由于工业用能环境的复杂性，用能系统的能耗过程会受到多种因素的干扰而呈现复杂的动态性，能耗P-规律揭示了能耗因子与用能系统能耗的动态关系，为能耗因子对用能系统能耗过程的干扰进行监控提供依据。本文把函数P-集的动态性和规律性应用于能源管理，应用MapReduce研究能耗规律，为能源管理特别是能耗监控管理提供新的理论和方法，为节能减排提供理论和技术支持。

参考文献：

［1］史开泉.函数P－集合［J］.山东大学学报(理学版)，2011，46（2）：62－69.

［2］SHI K Q.Function P－sets［J］.International Journal of machine Learning and Cybernetics，2011，2（4）：281－288.

［3］史开泉.P－集合，逆P－集合与信息智能融合－过滤辨识［J］.计算机科学，2012，39（4）：1－13.

［4］林蓉，史开泉.函数 P－集合和信息规律的属性控制［J］.计算机科学，2012，39（7）：225－228.

［5］邱锦明，夏佳荣，史开泉.F－干扰规律生成与它的特征识别［J］.山东大学学报(理学版)，2007，42（8）：36－41.

［6］卢伟业，李越胜，冯国行，等.一种用于燃天然气蒸汽锅炉热效率的快速预测方法［J］.节能技术，2017，35（1）：21－25.

［7］陈吉荣，乐嘉锦.基于 Hadoop 生态系统的大数据解决方案综述［J］.计算机工程与科学，2014，35（10）：25－35.

［8］史开泉.P－推理与信息的P－推理发现－辨识［J］.计算机科学，2011，38（7）：1－9

［9］李豫颖，林宏康，史开泉.数据离散区间特征与数据发现－应用［J］.系统工程与电子技术，2011，33（10）：2258－2262.

［10］宋杰，刘雪冰，朱志良，等.一种能效优化的 MapReduce 资源比模型［J］.计算机学报，2014，33（1）：59－73

［11］黄山，王波涛，王国仁，等.MapReduce 优化技术综述［J］.计算机科学与探索，2013，7（10）：855－885.