一致光滑逼近函数及其性质

雍龙泉

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

绝对值函数φ(t)=t在t=0处不可微，鉴于绝对值函数在非光滑优化理论及变分不等式中具有重要意义，因此研究绝对值函数的光滑逼近函数具有重要的实际意义[1-6]。φ(t)=t等价于φ(t)=max{t,-t}，文献[7]给出了绝对值函数的光滑处理方法以及在摩擦接触问题中的应用；文献[8-13]给出了绝对值函数φ(t)=t的一些逼近函数，并分别应用于求解绝对值方程；文献[14]研究了极大值函数max{0,t}的一类光滑逼近函数；文献[15]研究了绝对值函数的上方一致光滑逼近函数和下方一致光滑逼近函数。

本文在上述文献的基础上，较为系统地给出绝对值函数的7个一致光滑逼近函数，从理论上分析这些光滑逼近函数的性质及逼近程度，最后指出了一致光滑逼近函数的应用前景。

定义1(光滑逼近函数)[15]给定非光滑函数f(t):=R→R，我们称光滑函数f(μ,t),μ>0为f(t)的光滑逼近函数，如果对任意t∈R，存在κ>0，使得

f(μ,t)-f(t)≤κμ， ∀μ>0。

如果κ不依赖于t，则称f(μ,t)为f(t)的一致光滑逼近函数。

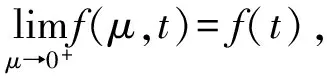
1 一致光滑逼近函数

下面给出绝对值函数φ(t)=t的7个光滑函数φi(μ,t)，它们在(μ,t)∈R++×R上是连续可微的。φi(μ,t),i=1,2,…,7，定义如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

图1—图3分别给出了μ=0.4,μ=0.2,μ=0.1时φi(μ,t),i=1,2,…,7与φ(t)=t的图像。

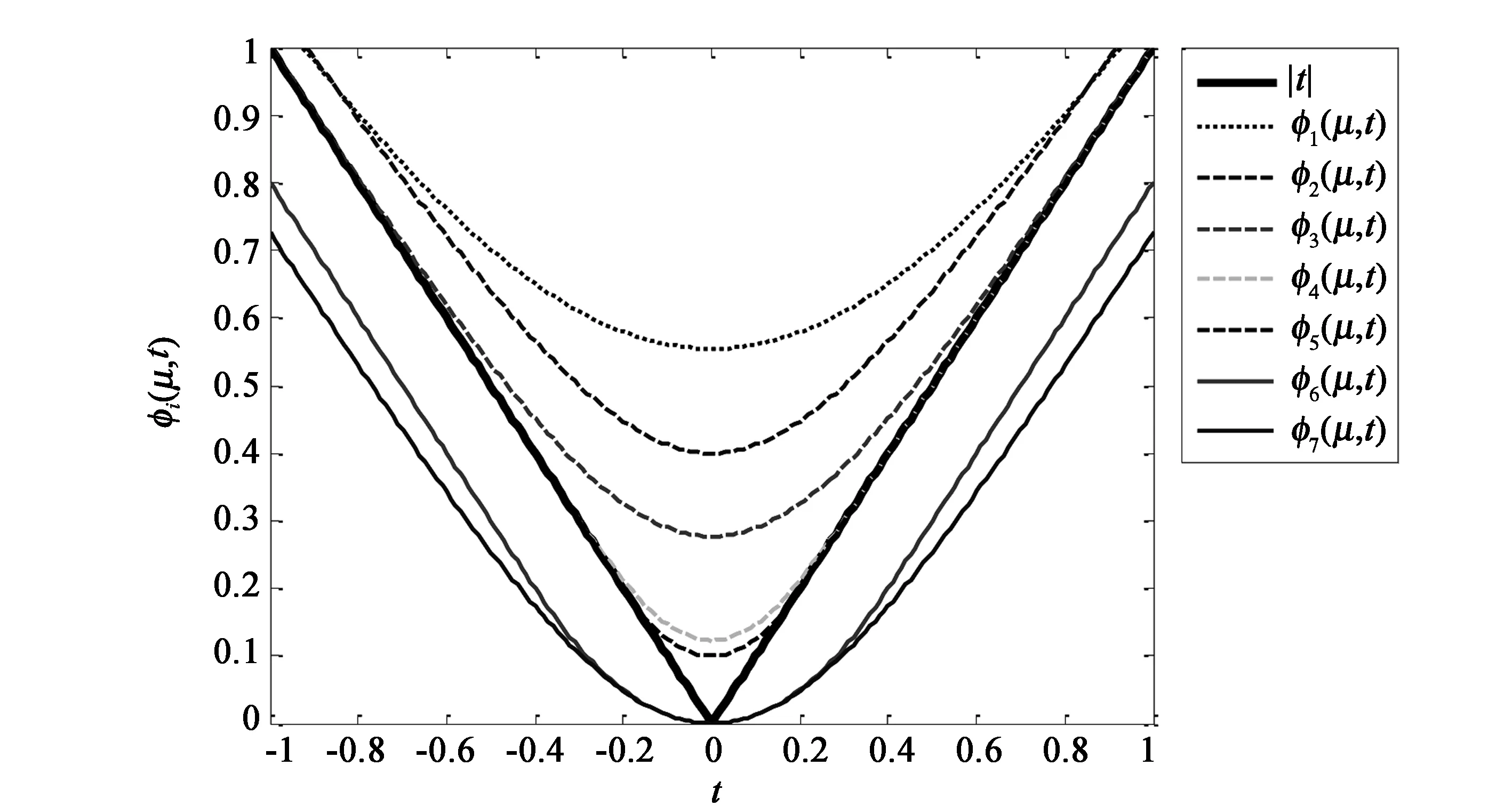
图1 μ=0.4时φi(μ,t),i=1,2,…,7与φ(t)=t的图像

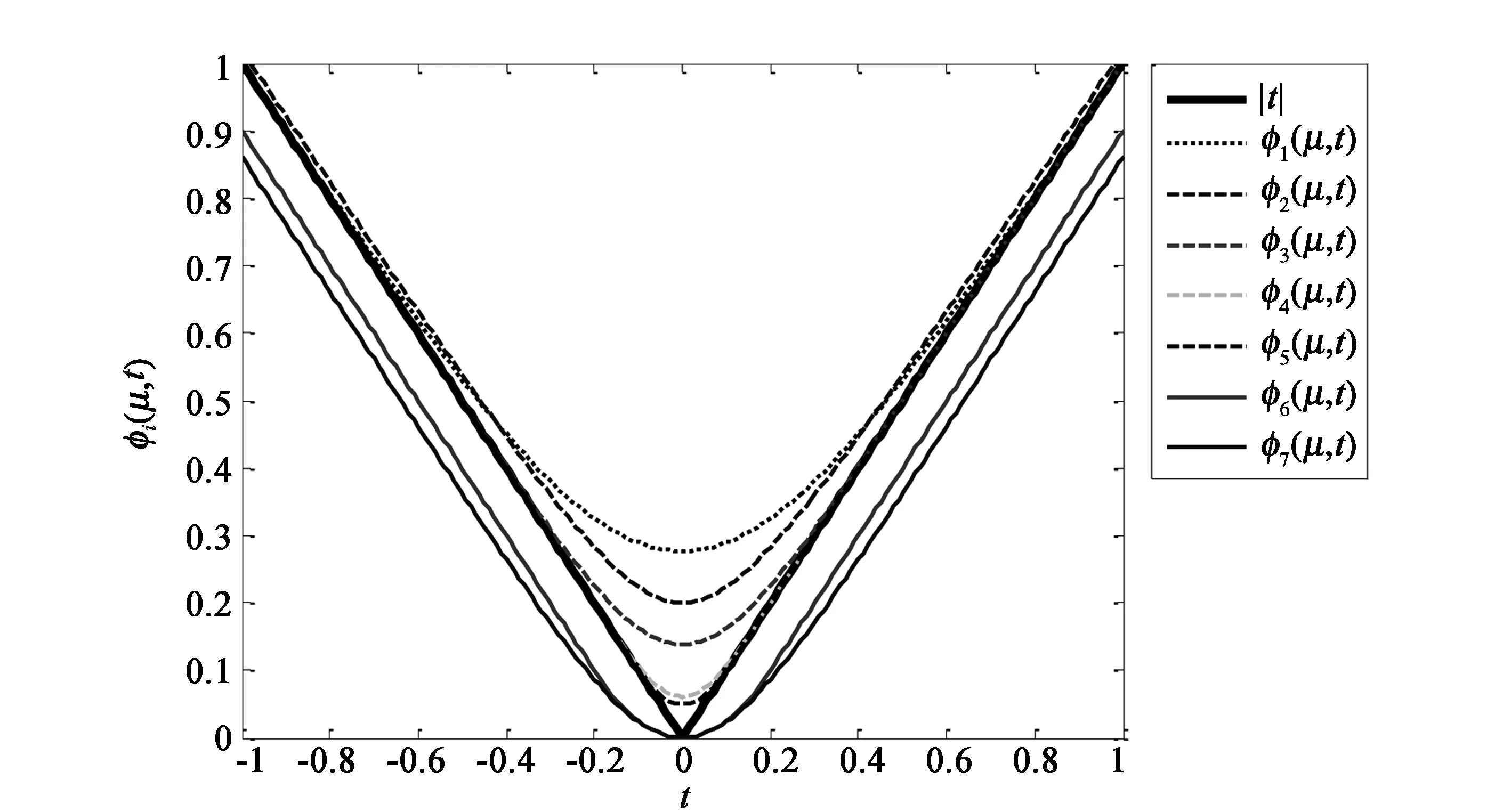
图2 μ=0.2时φi(μ,t),i=1,2,…,7与φ(t)=t的图像

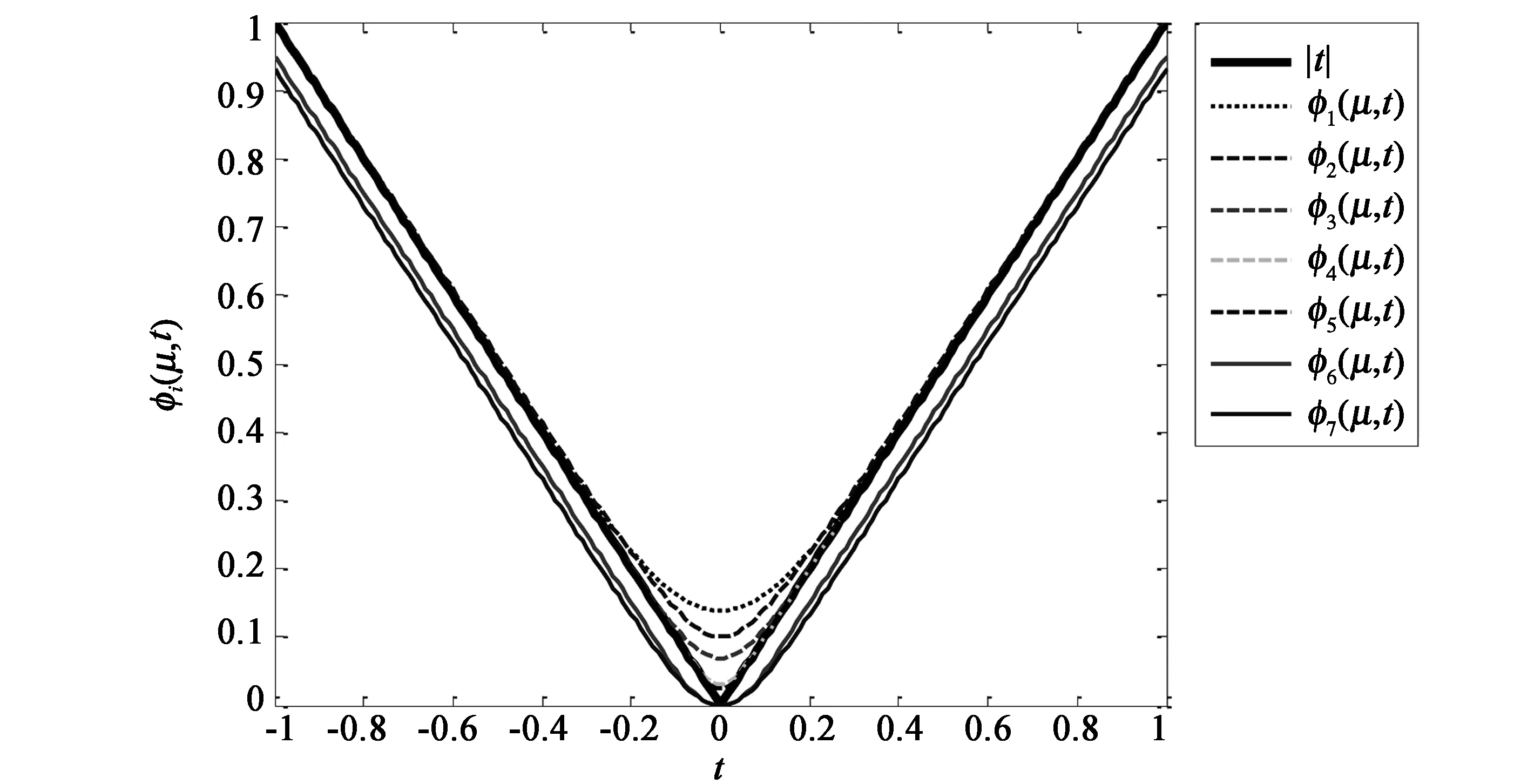
图3 μ=0.1时φi(μ,t),i=1,2,…,7与φ(t)=t的图像

2 一致光滑逼近函数的性质

下面给出7个光滑函数φi(μ,t),i=1,2,…,7的性质，因为篇幅的原因，证明省略。

命题1 函数φ1(μ,t)在(μ,t)∈R++×R具有如下性质：

(1) 0<φ1(μ,t)-φ(t)≤μln 4；

命题2 函数φ2(μ,t)在(μ,t)∈R++×R具有如下性质：

(1) 0<φ2(μ,t)-φ(t)≤μ；

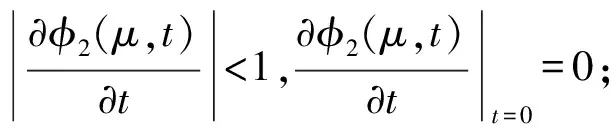
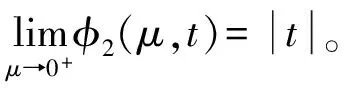
命题3 函数φ3(μ,t)在(μ,t)∈R++×R具有如下性质：

(1) 0<φ3(μ,t)-φ(t)≤μln 2；

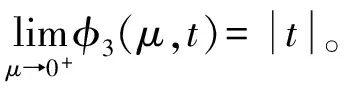
命题4 函数φ4(μ,t)在(μ,t)∈R++×R具有如下性质：

(1) 0≤φ4(μ,t)-φ(t)≤μ(1-ln 2)；

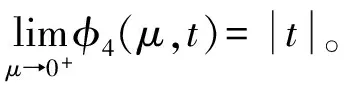
命题5 函数φ5(μ,t)在(μ,t)∈R++×R具有如下性质：

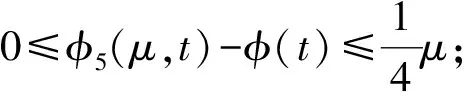
命题6 函数φ6(μ,t)在(μ,t)∈R++×R具有如下性质：

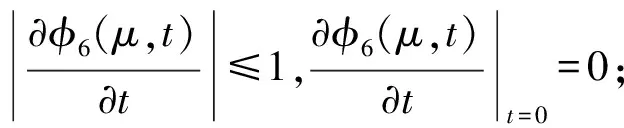
命题7 函数φ7(μ,t)在(μ,t)∈R++×R具有如下性质：

(1) -μln 2<φ7(μ,t)-φ(t)≤0；

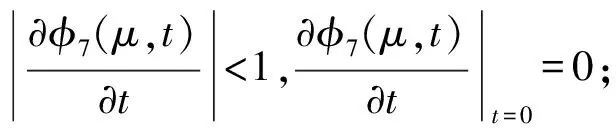
以上给出了7个光滑函数一些性质，这些性质可以用微积分简单推导出来，在此不再详述。

下面以定理的形式给出7个一致光滑逼近函数共同具有的性质。

定理1φi(μ,t),i=1,2,…,7分别按照上面的定义，则φi(μ,t),i=1,2,…,7满足：

(1)φi(μ,t),i=1,2,…,7在(μ,t)∈R++×R上是φ(t)的一致光滑逼近函数，其中φi(μ,t),i=1,2,3,4,5从上方一致逼近；φi(μ,t),i=6,7从下方一致逼近；

(2)φi(μ,t),i=1,2,…,7在(μ,t)∈R++×R上是连续可微的，且都满足

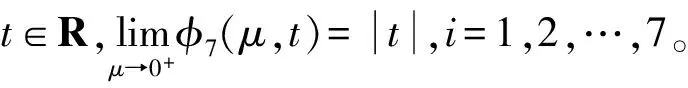
3 一致光滑逼近函数的逼近程度

当μ→0+时，下面来描述φi(μ,t),i=1,2,…,7与φ(t)=t的逼近程度。

从图1—图3可知在i=1,2,…,7的所有φi(μ,t)中，φ5(μ,t)逼近t的程度最好。为了说明这一点，采用无穷范数来度量两个实值函数之间的距离，即对于给定的两个实值函数f(t)和g(t)，定义它们之间的距离为

对于任意给定的μ>0，由于

这意味着

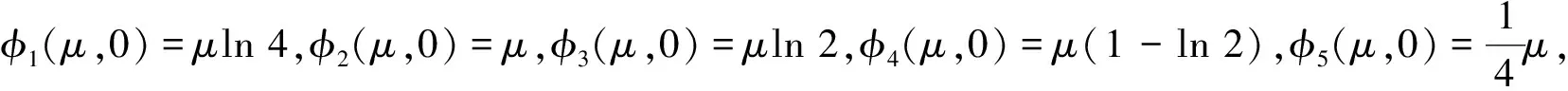
因此，从上方逼近而言得出结论：

这表明，在所有的上方逼近函数φi(μ,t),i=1,2,3,4,5中，φ5(μ,t)逼近φ(t)=t的程度最好。实际上，对于固定的μ>0，

φ1(μ,t)>φ2(μ,t)>φ3(μ,t)>φ4(μ,t)>φ5(μ,t)>t。

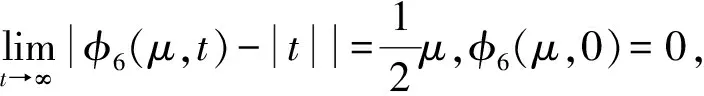
因此，从下方逼近而言得出结论：

这表明，在所有的下方逼近函φi(μ,t),i=6,7中，φ6(μ,t)逼近φ(t)=t的程度最好。实际上，对于任意给定的μ>0，

φ7(μ,t)<φ6(μ,t)

综上所述，对于任意给定的μ>0有如下结论：

φ1(μ,t)>φ2(μ,t)>φ3(μ,t)>φ4(μ,t)>φ5(μ,t)>t>φ6(μ,t)>φ7(μ,t)。

表1 φi(μ,t)与φ(t)=t之间的距离

从表1中的数据也可得出，φ5(μ,t)与φ(t)=t之间的距离最小，从而φ5(μ,t)逼近φ(t)=t的效果最好。

4 结束语

绝对值函数φ(t)=t的一致光滑逼近函数在数值逼近[16]、非光滑优化[17]、神经网络[18-20]等领域具有重要的科学意义，限于篇幅，关于绝对值函数的一致光滑逼近函数的应用，将另行讨论。此外，在上述光滑逼近函数φi(μ,t)，i=1,2,…,7中，如果把μ换成其等价无穷小量sinμ，0<μ<1，则逼近效果更好。

[参考文献]

[1] CHEN Chun-hui,MANGASARIAN O L.A class of smoothing functions for nonlinear and mixed complementarity problems[J].Computational Optimization and Applications,1996,5(2):97-138.

[2] QI L,SUN D.Smoothing Functions and A Smoothing Newton Method for Complementarity and Variational Inequality Problems[J].Journal of Optimization Theory and Applications,2002,113(1):121-147.

[3] QI L,CHEN X.A Globally Convergent Successive Approximation Method for Severely Nonsmooth Equations[J].SIAM Journal on Control & Optimization,2006,33(2):402-418.

[4] HUANG Z H,ZHANG Y,WU W.A smoothing-type algorithm for solving system of inequalities[J].Journal of Computational & Applied Mathematics,2008,220(1):355-363.

[5] ZHANG Y,HUANG Z H.A nonmonotone smoothing-type algorithm for solving a system of equalities and inequalities[J].Journal of Computational & Applied Mathematics,2010,233(9):2312-2321.

[6] WANG F,YU Z,GAO C.A Smoothing Neural Network Algorithm for Absolute Value Equations[J].Engineering,2015,7(9):567-576.

[7] 张洪武,何素艳,李兴斯.求解摩擦接触问题的一个非内点光滑化算法[J].应用数学和力学,2004,25(1):42-52.

[8] CACCETTA L,QU Biao,ZHOU Guang-lu.A globally and quadratically convergent method for absolute value equations[J].Computational Optimization and Applications,2011,48(1):45-58.

[9] 雍龙泉,拓守恒.基于凝聚函数的拟牛顿算法求解绝对值方程[J].系统科学与数学,2012,32(11):1427-1436.

[10] ESMAEILI H,MAHMOODABADI E,AHMADI M.A uniform approximation method to solve absolute value equation[J].Bulletin of the Iranian Mathematical Society,2015,41(5):1259-1269.

[11] 雍龙泉.基于调节熵函数的光滑牛顿法求解绝对值方程[J].兰州大学学报(自然科学版),2016,52(4):540-544.

[12] YONG Long-quan.A Smoothing Newton Method for Absolute Value Equation[J].International Journal of Control and Automation,2016,9(2):119-132.

[13] SAHEYA B,YU C H,CHEN J S.Numerical comparisons based on four smoothing functions for absolute value equation[J].Journal of Applied Mathematics & Computing,2016(10):1-19.

[14] 张丽丽,李建宇,李兴斯.极大值函数的一类光滑逼近函数的性质研究[J].数学的实践与认识,2008,38(24):229-234.

[15] 雍龙泉.绝对值函数的一致光滑逼近函数[J].数学的实践与认识,2015,45(20):250-255.

[16] 王仁宏.数值逼近[M].北京:高等敎育出版社,1999.

[17] 萨和雅.非线性方程组的锥模型方法研究[D].呼和浩特:内蒙古大学,2017:69-78.

[18] CHEN J S,KO C H,PAN S.A neural network based on the generalized Fischer-Burmeister function for nonlinear complementarity problems[J].Information Sciences,2010,180(5):697-711.

[19] SUN J,CHEN J S,KO C H.Neural networks for solving second-order cone constrained variational inequality problem[J]. Computational Optimization and Applications,2012,51(2):623-648.

[20] MIAO X,CHEN J S,KO C H.A neural network based on the generalized FB function for nonlinear convex programs with second-order cone constraints[J].Neurocomputing,2016,203:62-72.