麻花钻的钻削参数对钛合金钻削性能的影响

沈 钰， 白海清

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

钛合金因具有热强度高、抗腐蚀性好、耐热性强等特点，被广泛应用于航空航天制造及医疗器械等领域。但是，钛合金作为一种典型的难加工材料，其导热性差、弹性模量小、化学活性强致使其易与刀具材料产生化学反应，切削温度高导致刀具磨损严重、加工效率低[1]。麻花钻钻削钛合金材料时，钻头的几何参数、刀具材料和切削用量是影响钛合金钻孔质量的主要因素，钻削力、钻削温度及刀具磨损则是反映钻削性能及加工过程的重要依据。

对于如何提高麻花钻钻削钛合金的钻孔质量，一直以来都是诸多学者研究的重点。韩荣第等[2]分析了钻头直径、钻削参数和刀具材料对钛合金钻削力的影响，结果表明钻头直径对钻削力影响最大，进给量次之，切削速度最小；南成根等[3]分析了碳纤维复合材料/钛合金叠层钻孔质量损伤的原因，结果表明钻削钛合金时产生的切屑是导致CFRP孔径超差的主要原因；胡立湘等[4]采用TiAlN涂层硬质合金麻花钻对钛合金(TC4)进行钻削试验，获得了切削用量对轴向力、加工孔壁表面粗糙度和形态的影响规律。

然而，以上研究采用的试验方式均为传统方式，存在周期长、成本高、场地受限等局限。故本文以钛合金(Ti6Al4V)为研究对象，采用高效便捷的有限元仿真技术来弥补传统试验方式的不足。

本文基于DEFORM-3D软件，并结合正交试验方法，以钻头直径d、切削速度vc、进给量f这3个变量为影响因素，研究麻花钻钻削钛合金过程中，麻花钻轴向力的变化。通过极差和方差分析，确定各因素的主次顺序及最优参数组合，并检验各因素的显著性。根据正交试验数据，结合MATLAB软件进行多元线性回归分析，建立钻削力的数学模型，并对经验公式计算与仿真数据对比分析。

1 DEFORM-3D钻削有限元仿真

1.1 麻花钻模型的建立

对于麻花钻模型的建立，本文采用DEFORM-3D软件自身的三维建模功能，通过文献[5]确定麻花钻的几何参数和刃磨参数后默认建模，其参数设置界面如图1所示。对于DEFROM-3D软件中标准麻花钻默认建模的合理性，可通过麻花钻的横刃方程公式(1)和后角方程公式(3)计算验证[6]，验证其建模后的标准麻花钻后角和横刃斜角是否在合理值范围内，如果角度值合理，则进一步证明了标准麻花钻模型的准确性。

横刃方程：

(1)

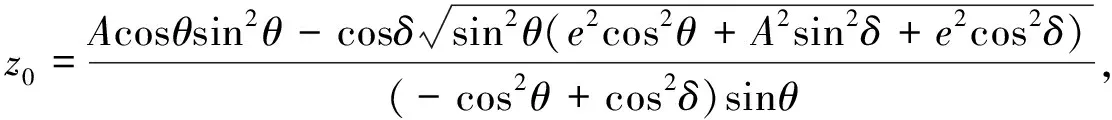
(2)

后角方程：

(3)

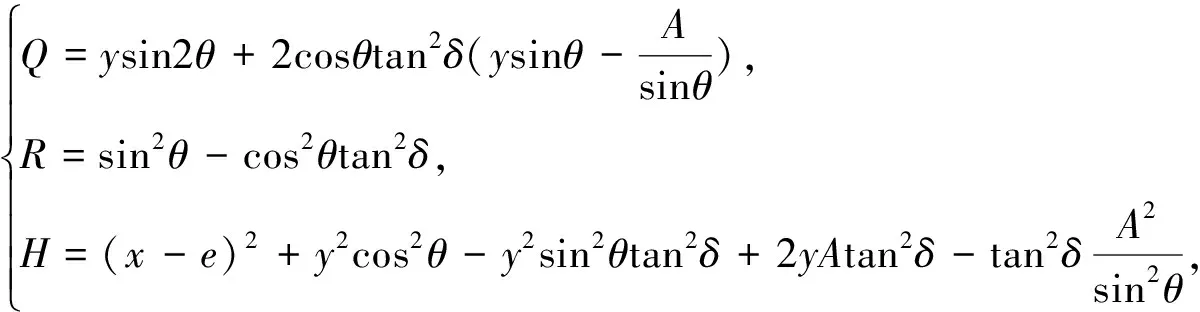
(4)

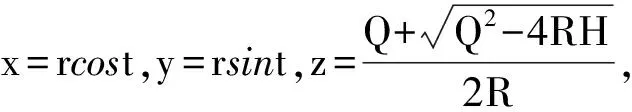
1.2 预处理参数设置

1.2.1 刀具与工件参数设置

本文机械加工类型选择钻孔采用国际单位制SI标准，刀具设为刚性模型，材料选用硬质合金；工件设为塑性模型，其形状选择直径为16 mm，高度为6 mm的圆柱体，材料选用钛合金(Ti6Al4V)，主要性能参数如表1所示，金属材料的本构模型采用Johnson-Cook(J-C)模型。DEFORM-3D软件采用自适网格划分(AMG)技术，其目的是为了保证在有限元分析过程中出现的不合格单元形状的网格能够即时重新划分，确保网格的收敛性，从而确保仿真结果的准确性[7]。刀具采用相对网格划分，设置网格数为20 000，size ratio为4；工件采用绝对网格划分，设置最小单位边长小于进给量的1/2，即最小网格尺寸小于单刃进给量，size ratio为7。在边界条件中，设置工件侧面与底面在X、Y、Z方向上的速度均为0，其目的是确保工件静止；刀具沿-Z方向做进给运动并绕自身轴线旋转。

表1 钛合金的主要性能参数

图2 钻削有限元仿真模型

1.2.2 工作状态参数设置

在DEFORM-3D软件中，环境温度设为20 ℃；对流系数为0.02 N/s/mm/C；定义摩擦类型为剪切摩擦，摩擦系数设为0.6；热传导系数为45 N/s/mm/C。

1.2.3 模拟参数设置

模拟运算总步数10 000步，每25步存储1次；求解器采用共轭梯度求解，迭代方法为直接迭代法；刀具磨损模型采用经验公式Usui模型，设置参数a为1×10-6，b为855。

在Database generation对话框中，单击Check按钮，数据库检查确认无误后，单击Generate按钮生成DB文件，生成的钻削有限元仿真模型见图2所示。

2 正交试验设计

2.1 试验内容及方法

本文的目的是研究钻头直径d(mm)、钻削速度vc(m/min)、进给量f(mm/r)3个因素对麻花钻轴向力的影响，故以摇臂钻床Z3040×16为试验目标，采用3水平3因素的试验因素水平表，如表2所示。

表2 试验因素水平表

采用L9(34)的正交试验表，利用DEFORM-3D软件对9组数据进行有限元仿真分析，并以麻花钻的轴向力Fz(kN)作为钻削性能指标，其钻削正交试验安排及结果如表3所示。

2.2 钻削轴向力分析

对于麻花钻轴向力在钻削过程中的变化趋势如图3所示，其中X轴代表时间(Time，单位为s)，Y轴代表轴向力(Z Load，单位为kN)。由图分析可知，轴向力变化趋势先是不断上升，后逐渐趋于平稳，并在平稳阶段内上下波动。分析其原因可能是由于网格即时重新划分时造成仿真过程的不连续和切屑的变形或断裂而引起的[6]。

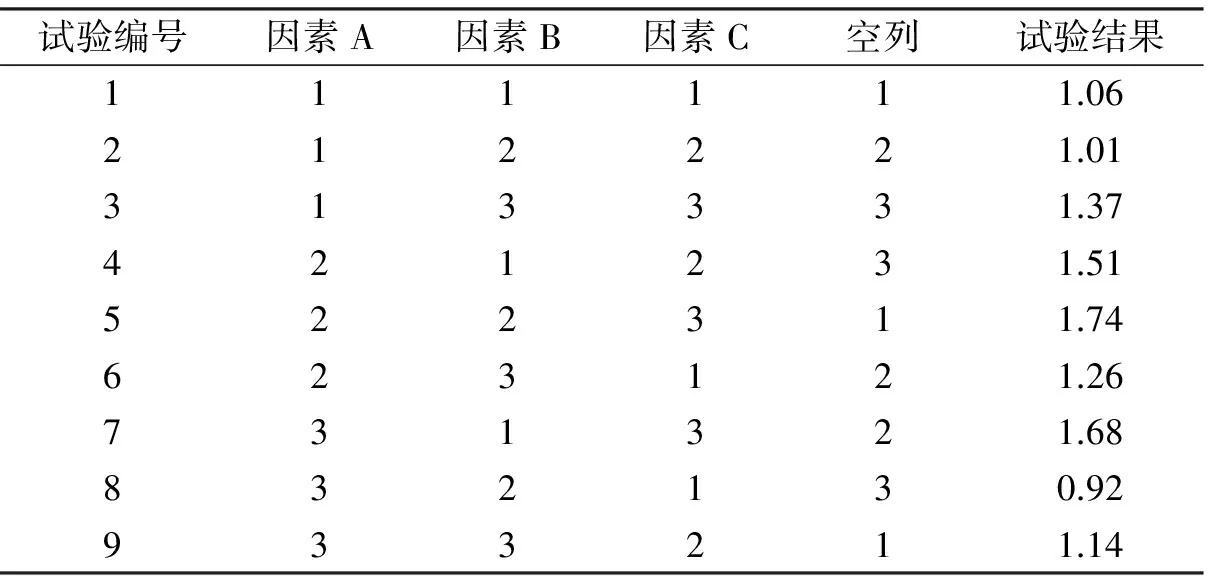
表3 钻削正交试验安排及结果

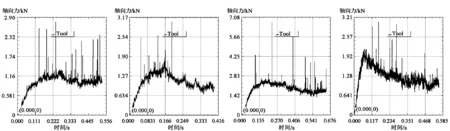
(a) d=6 mm，vc=12 m/min， (b) d=6 mm，vc=18 m/min， (c) d=10 mm，vc=12 m/min， (d) d=10 mm，vc=24 m/min， f=0.20 mm/r f=0.24 mm/r f=0.28 mm/r f=0.24 mm/r图3 钻削轴向力变化曲线图

2.3 正交试验结果的极差与方差分析

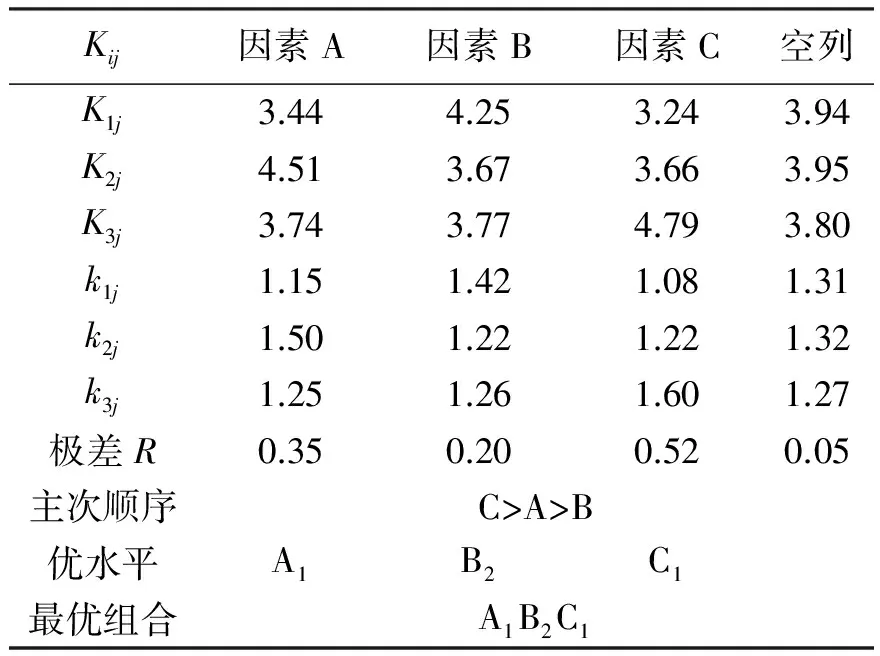
表4 极差分析表

注：kij为Kij的平均值；极差R为kij中最大值与最小值之差。

根据正交试验的仿真结果，本文对于轴向力仿真数据进一步进行了极差分析，以图表的形式来确定各因素的主次顺序及最优钻削参数组合。然而，各因素对试验结果的影响程度，即各因素作用的显著性，还无法准确地体现出来[8]。因此，还需对试验结果进行方差分析，从而弥补上述分析的不足。分析结果如表4、表5、图4所示，表5中各参数计算公式如下[9]：

fj=n-1,σj=SSj/fj,Fj=σj/σ, (6)

式中：SSj为平方和；Kij为第j因素第i水平所对应的试验指标和；T为试验结果之和；fj为自由度；n为各因素水平个数；σj为均方；σ为总误差均方。

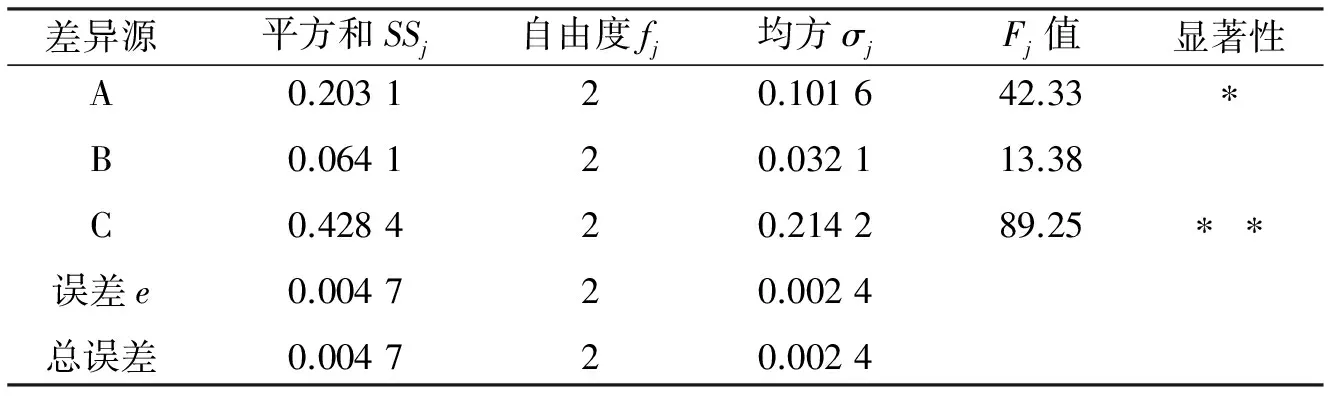
表5 方差分析表

(a) 钻头直径的影响 (b) 钻削速度的影响 (c) 进给量的影响图4 钻头直径、钻削速度和进给量对钻头轴向力的影响趋势图

由图4分析可知，在麻花钻钻削钛合金的过程中，钻头的轴向力随钻头直径d的增大，先增大后减小；随钻削速度vc的增大，先减小后增大；随进给量f的增大而增大。根据极差分析表(表4)及方差分析表(表5)可知，极差R的大小可判断选定的各因素的主次顺序，R值越大，表示该因素的水平变化对试验结果的影响越大。因此，进给量f(因素C)对钻头轴向力的影响最大且最为显著，钻头直径d(因素A)次之，钻削速度vc(因素B)影响最小。根据平均值大小选定各因素的最优水平，平均值越大，影响越大。在钻削过程中，麻花钻的轴向力主要是由横刃产生，而轴向力越小，越有利于提高横刃的定心精度，同时也能提高刀具的耐用度，延长使用寿命。因此，确定最优钻削参数组合为A1B2C1，即d=6 mm，vc=18 m/min，f=0.20 mm/r。

3 钻削力模型的建立

根据本文正交试验数据，利用MATLAB软件对其进行多元线性回归分析，建立钻削力的数学模型。根据金属切削原理，切削力与切削参数之间存在复杂的指数函数关系，故轴向力的通用形式为[10]：

(7)

式中：Fz为轴向力；CF为系数；XF、YF、ZF为指数。

对公式两边取对数换算，使之变换成线性函数：lgFz=lgCF+XFlgd+YFlgvc+ZFlgf，进一步化简，令y=lgFz，b0=lgCF，b1=XF，b2=YF，b3=ZF，x1=lgd，x2=lgvc，x3=lgf，则轴向力通用公式对应的回归方程为：

y=b0+b1x1+b2x2+b3x3。

(8)

将正交试验数据全部取对数后，遵循相应编程格式输入MATLAB软件中建立M文件，并采用多元线性回归函数regress函数对数据进行处理，具体操作如下[11]：

x1=[0.7782,0.7782,0.7782,0.9031,0.9031,0.9031,1,1,1];

x2=[1.0791,1.2553,1.3802,1.0791,1.2553,1.3802,1.0791,1.2553,1.3802];

x3=[-0.6990,-0.6198,-0.5528,-0.6198,-0.5528,-0.6990,-0.5528,-0.6990,-0.6198];

y=[3.0273,3.0045,3.1359,3.1781,3.2394,3.1014,3.2243,2.9613,3.0572];

X=[ones(length(y),1),(x1)’,(x2)’,(x3)’];

Y=y’;

[b,bint,r,rint,stats]=regress(Y,X);

b,bint,stats

程序运行后可得轴向力的回归方程为：y=3.890 3+0.151 7x1-0.167 8x2+1.145 9x3，

故轴向力的数学模型为：

Fz=7 767.835d0.151 7vc-0.167 8f1.145 9。

(9)

将选定的最优钻削参数组合代入DEFORM软件中进行仿真，获得仿真数据0.83，利用经验公式计算得0.99，比较两者的误差大小为16.16%，证明了经验公式的可行性。

4 结 语

(1)利用DEFORM-3D软件对钛合金材料钻削加工进行的有限元仿真试验，相比传统试验方式更加便捷、高效,且随着计算机及有限元分析软件的不断发展与完善，其仿真数据的精度将进一步提高；

(2)对于钻削参数对轴向力的影响，采用正交试验法，选取代表性试验点，并结合极差分析和方差分析，直观确定了各因素的主次顺序，得到进给量对麻花钻的轴向力影响最为显著，获得了最佳钻削参数组合，即d=6 mm，vc=18 m/min，f=0.20 mm/r；

(3)根据正交试验结果，利用MATLAB软件对其进行了多元线性回归分析，建立了钻削力的数学模型，通过利用经验公式与仿真数据的对比误差分析，进一步证明了经验公式的可行性；

(4)通过钛合金钻削过程的有限元分析，为麻花钻钻削钛合金材料的实际钻削加工过程中提高钻孔的质量、合理选择钻削参数提供了参考依据，为钻削参数的优化打下了基础。

[参考文献]

[1] 李克强.钛合金车削用PCD刀具优选及切削参数优化[D].哈尔滨:哈尔滨理工大学,2013.

[2] 韩荣第,吴健.钛合金TC4的钻削力试验研究[J].工具技术,2009,43(1):25-27.

[3] 南成根,吴丹,马信国,等.碳纤维复合材料/钛合金叠层钻孔质量研究[J].机械工程学报,2016,52(11):177-185.

[4] 胡立湘,李鹏南,陈明,等.TiAlN涂层钻头钻削钛合金的实验研究[J].宇航材料工艺,2016,46(2):48-52.

[5] 戴俊平.麻花钻内锥面刃磨试验[J].陕西理工学院学报(自然科学版),2003,19(1):7-9.

[6] 朱超,白海清.采用DEFORM-3D对钻削过程的有限元仿真[J].煤矿机械,2015,36(6):286-289.

[7] 高兴军,李萍,闫鹏飞,等.基于Deform 3D不锈钢钻削机理的仿真研究[J].工具技术,2011,45(4):17-20.

[8] 金浩,程寓,高超,等.玻璃钢复合材料夹层结构钻削试验研究[J].机械设计与制造,2011(4):133-135.

[9] 张利新,沈兴全,张晓,等.基于正交试验的麻花钻钻削钛合金的刃磨参数选择[J].现代制造工程,2013(6):8-11.

[10] 陆建中,孙家宁.金属切削原理与刀具[M].北京:机械工程出版社,2011.

[11] 朱超,白海清.基于DEFORM-3D和遗传算法的钻削用量优化研究[J].工具技术,2016,50(1):48-51.