风电变桨轴承套圈应力及失效分析

周志宏，郑广,彭雄文，余礼，吕涨，殷卓成 (长江大学机械工程学院，湖北 荆州 434023)

风力发电变桨轴承是大型风力发电机组传动系统的关键部件，其可靠性对于控制功能实现和运行安全有重要影响。国内外对于变桨轴承承载能力的研究较多。2011年，王思明等[1]根据受力与变形的关系推导变桨轴承滚道上载荷分布的计算公式，求解得出每个滚动体上的载荷分布情况，通过实例计算得出在某一负游隙时具有最大承载能力，受载轴承的沟道上接触载荷呈正弦曲线分布。2012年王燕霜和袁倩倩等[2,3]基于静力学建立了变桨轴承载荷分布的分析模型，得到不同游隙及载荷下滚动体承受的最大接触载荷，然后根据L-P理论计算变桨轴承的额定疲劳寿命，认为轴承额定寿命随着轴承负游隙的绝对值增大，轴承寿命先增大后减小，轴承沟曲率系数越大疲劳寿命越小。同年，贾平和陈观慈等[4]利用有限元软件仿真模拟轴承，使用非线性的弹簧单元combin39以及刚性的梁单元MPC184代替滚动体，计算了轴承在连接上轮毂之后的变形情况，讨论了连接的刚度对于轴承整体变形的影响。2013年，芮晓明等[5]在一般的静力学模型上引入薄壁圆环平面弯曲理论，将套圈视为柔性建立力学平衡方程并求解，并与传统的将套圈视为刚性的求解结果对比，认为将套圈视为柔性才能更加客观地反映轴承实际的载荷分布情况。2014年黄浙等[6]建立了大型的变桨轴承在受到联合载荷作用下有限元模型，对ANSYS进行了二次开发，将轴承的结构参数加入有限元的GUI中，使得轴承的计算更加简便，加快了变桨轴承的几何参数对于轴承最大的承载能力的影响的计算效率。

变桨轴承是调整风电设备中叶片迎风角度的重要部件，一般采用特大型的单排或者双排4点接触球轴承。变桨轴承主要在重载、极低速度的摆动状态，同时承受多向力、弯矩等复杂交变载荷。变桨轴承安装方式特殊，内外圈端面分别用螺栓连接在叶片与轮毂上，安装轴承的过程中，滚动体是通过安装孔进入内外套圈之间，然后使用带销的塞将安装孔堵住，所以安装孔处在套圈中是比较薄弱的环节。某风场风力发电设备中，变桨轴承在使用2年后有部分变桨轴承安装孔附近几颗螺栓有松动情况，外套圈安装位置有裂纹产生，裂纹宽度约为5mm。为此，笔者以该变桨轴承为例，基于赫兹接触理论建立套圈承受多向载荷下的静力学模型，求解轴承滚动体的载荷分布情况，并使用有限元建立套圈模型，重点分析轴承套圈安装孔处的应力分布情况，研究变桨轴承外套圈开裂原因。

1 变桨轴承静载荷计算

1.1 模型分析

静力学分析时，以轴承的径向承受载荷方向为X方向，以轴承径向承受载荷垂直方向为Y方向，轴承的轴向为Z方向，建立变桨轴承力学模型，如图1所示。

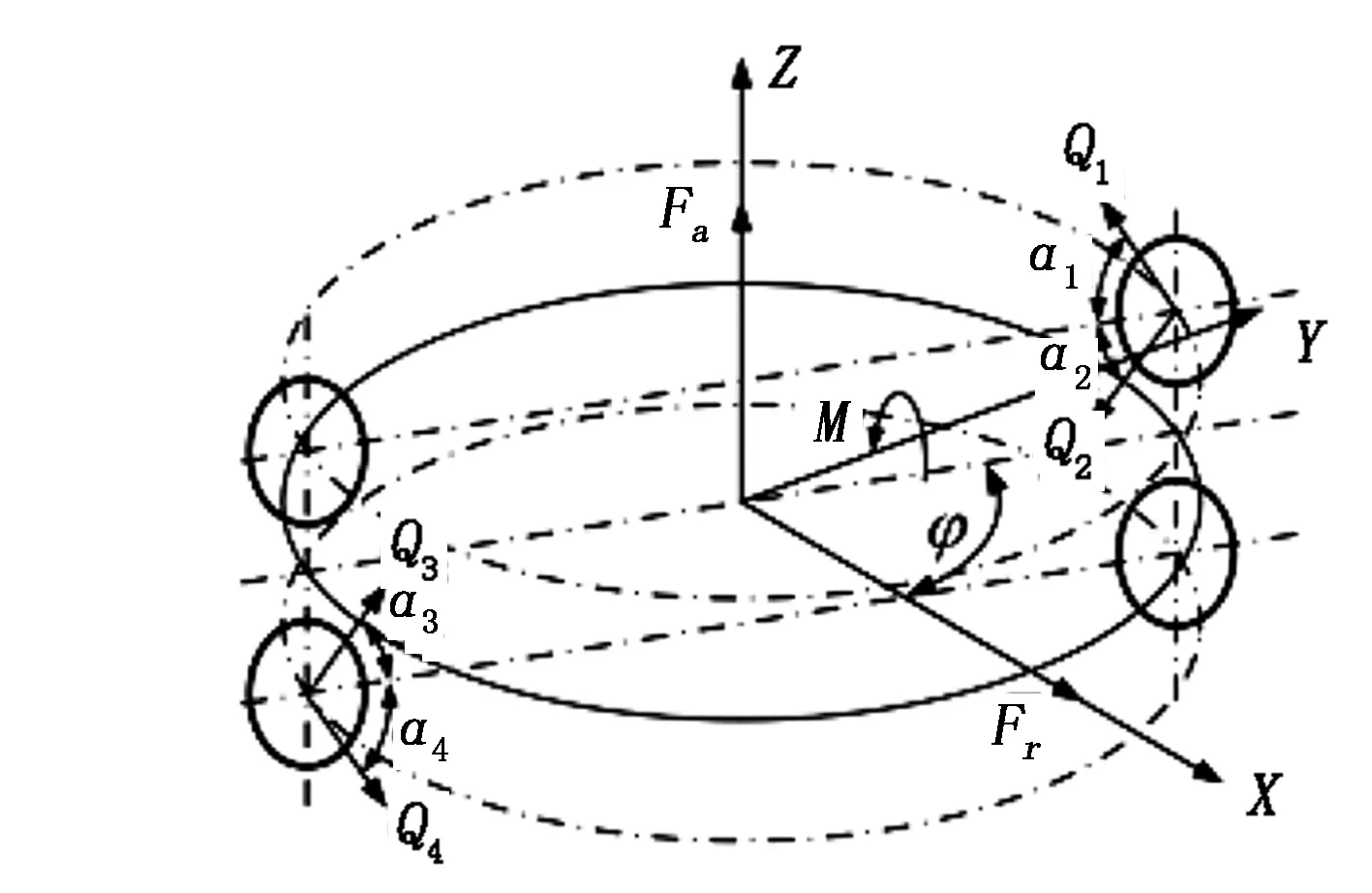
图1 变桨轴承力学模型

图2 接触对变形模型

变桨轴承安装时桨叶通过螺栓与轴承内圈连接，外圈通过螺栓与轮毂连接，叶片受到的风载以及重力由滚动体传输到轮毂。图1中，Fa为轴承承受的轴向载荷，Fr为轴承承受的径向载荷，M为轴承承受的倾覆力矩。变桨轴承为双排4点角接触球轴承，每个滚动体上主要有2个接触对用来传递载荷，将每个滚动体受载的接触对从上往下定义为接触对1、接触对2、接触对3以及接触对4。在位置角φ处，上排滚动体受到的载荷为Q1，Q2，对应的接触角为α1和α2；下排滚动体受到的载荷为Q3，Q4，对应的接触角为α3，α4。

轴承内外圈之间的载荷由滚动体传递，其中轴承内外套圈之间沟曲率中心距可以很好地反映出滚动体受到挤压的情况：沟曲率中心距越大滚动体受到的载荷就越大，沟曲率中心距小于原始沟曲率中心距时滚动体不承受载荷。

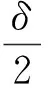
轴承受载前任意位置角截面中内外沟曲率中心距为：

(1)

式中，fi为内沟道曲率半径系数；Dw为滚动体直径，mm；f0为外沟道曲率半径系数；Ga为轴承的轴向游隙，mm；α0为轴承未受载前的名义接触角，(°)。

变桨轴承外套圈通过螺栓固定于轮毂上，内套圈用于安装叶片，所以静力学分析时将外套圈视为固定，内套圈在叶片承受载荷情况下相对外套圈产生相对位移。相对位移会导致滚动体与滚道产生接触载荷，根据赫兹接触理论滚动体承受的接触载荷可由接触产生的弹性变形量求出。

内外圈的相对位移可分解为3个方向相对位移：相对轴向位移δa、相对径向位移δr以及相对转角θ。内外圈的相对位移也会导致内外圈的沟道曲率中心距发生变化，变化后的沟道曲率中心距可由内外圈的3个相对位移投影到不同位置角求出。

以位置角φ所在的平面内接触对1为例，产生位移后沟曲率中心距轴向分量为：

A1φa=Asinα0+δa+Riθcosφ

(2)

(3)

式中，θ为内外圈相对转角，(°)；Dpw为滚动体节圆直径，mm；δa为轴向位移，mm；Ri为内圈沟曲率中心轨迹半径，mm。

产生位移后接触对1的沟曲率中心距径向分量为：

A1φr=Acosα0+δrcosφ+0.5dcθcosφ

(4)

受载后在位置角φ处接触对i的沟曲率中心距Aiφ变为：

(5)

内圈发生相对位移后，在位置角φ处接触对i的实际接触角αiφ为：

(6)

1.2 力学平衡方程

(7)

根据力学平衡条件，内圈在承受外部载荷与滚动体的接触载荷下处于平衡状态，可以得到平衡方程：

式(8)～式(10)是关于轴向位移δa、径向位移δr和转角θ的非线性方程组，对于给定的外部载荷，利用Newton-Raphson方法进行数值迭代可以得到计算结果，根据计算结果可求出变形后的沟曲率中心距，然后代入式(7)就可以算出各位置角处滚动体的载荷分布情况。

2 轴承套圈有限元模型

轴承外套圈安装孔处形状复杂，而有限元计算精度高，能准确计算出安装孔位置的应力状态，所以采取有限元软件对轴承外套圈进行计算。轴承套圈使用材料为42CrMo合金钢，整体材料屈服强度取930MPa，泊松比取0.3，抗拉强度取1080MPa，弹性模量取212000MPa。

在建模过程中，用工作平面将滚动体与沟道接触点切出来方便加载，如图3所示；将基于静力学模型计算出滚动体载荷，用参数化方法分解为3个方向上的力，施加在滚动体与套圈接触的位置，如图4所示。根据实际的载荷情况改变套圈的约束情况来计算安装孔位置应力状态。

图3 有限元外套圈模型 图4 变桨轴承外套圈载荷及约束模型

3 实例计算

取某兆瓦级风力发电装置中的变桨轴承[7]，轴承参数及受载情况如表1所示。

代入程序计算出每个滚动体受到的载荷情况，经过计算内外套圈产生的相对转角位移为0.016256°，相对轴向位移为0.0586mm，相对径向位移为0.1023mm。

表1 变桨轴承技术参数

图5 接触对载荷分布图

图6 轴承外套圈安装孔位置第一主应力分布

通过变桨轴承实际承受载荷数据分析可知，倾覆力矩的作用效果远远大于轴向载荷和径向载荷。在计算实例中针对轴承只承受倾覆力矩的情况作详细计算，变桨轴承实例中轴承各参数代入程序中求出结果，将角位移代入赫兹接触理论计算出每个位置角处滚动体承受的载荷，结果如图5所示。

外套圈承受滚动体传递载荷，端面由螺栓连接在轮毂上。将套圈端面约束Z方向自由度，将螺栓孔约束X,Y方向自由度。根据检查拆卸的轴承螺栓松动情况，安装孔附近有4颗螺栓有松弛15～20°左右，根据螺栓组的受载情况这几颗螺栓也是受载最大。所以分3种约束条件来计算安装孔位置应力分布情况：对所有螺栓孔X,Y方向自由度约束；对称放松安装孔附近2颗螺栓，剩余螺栓孔X,Y方向自由度约束；对称放松安装孔附近4颗螺栓，剩余螺栓孔X,Y方向自由度约束。

图6为放松4颗螺栓孔约束计算得出的安装孔位置第一主应力(即拉应力)分布情况，其中套圈最大拉应力位置与实际情况中套圈开裂位置相符。相应的3种情况计算出安装孔位置第一主应力如表2所示。

表2 安装孔位置应力情况

根据套圈开裂的位置与方向，笔者认为套圈失效为随机风载导致的疲劳失效。套圈由于循环变应力及塑性变形导致垂直于拉应力方向裂纹的产生，然后以极快的速度向为45°方向扩展，其中拉应力占主要作用。所以取计算得出最大拉应力代入ASME疲劳设计曲线[8]来分析套圈开裂原因。

变桨轴承实际工作中承受的载荷为随机脉动载荷，将计算出的最大静拉应力视为脉动循环载荷中的最大应力，最小应力为0。考虑到平均应力的影响，将该脉动循环载荷的应力幅值代入Goodman公式:

(11)

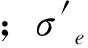
通过式(11)将脉动循环载荷应力幅值转化为交变循环载荷的应力幅值为259.735MPa。

将ASME曲线进行四参数拟合得出应力幅值与循环次数的关系式如下：

(12)

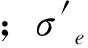
将对称循环载荷的应力幅值代入ASME疲劳设计曲线中可以求出在该应力幅值水平下的循环次数约为18315次，实际变桨轴承工作情况每年风载的循环次数都远远超过该次数，即使考虑到大部分随机载荷的值小于最大载荷，该点也有很大可能超过设计疲劳寿命。而变桨轴承在该应力幅值下持续工作就会导致轴承套圈安装孔位置裂纹的产生。

4 结论

1)基于赫兹接触理论建立静力学模型求解变桨轴承载荷分布情况，采用有限元建立套圈模型并将载荷以数值形式加载在套圈上模拟不同约束条件下套圈安装孔位置应力分布情况。结果表示，在安装孔附近有4颗螺栓松动的情况下拉应力达到415.35MPa。

2)将计算的脉动循环载荷转化为等效对称循环载荷代入ASME疲劳设计曲线求出在该应力幅值水平下循环次数约为18315次。该次数远小于实际工作的需求，所以认为螺栓松弛导致安装孔位置应力急剧增大是导致轴承外套圈安装孔开裂原因，建议固定螺栓预紧力定期检查，保证变桨轴承正常工作。

[参考文献]

[1]王思明，罗继伟，许明恒.风力发电机变桨轴承力学分析[J].中国工程机械学报，2011, 9(3)：73～76.

[2]王燕霜，袁倩倩.负游隙对特大型双排四点接触球轴承载荷分布的影响[J].机械工程学报，2012, 48(11)：110～115.

[3]王燕霜，袁倩倩，曹佳伟，等.特大型四点接触轴承承载能力的研究[J].机械工程学报，2014, 50(5)：66～70.

[4]贾平.偏航变桨轴承力学特性分析及结构优化设计[D].大连：大连理工大学,2012.

[5]芮晓明，郑辉，黄浩然.风电机组变桨轴承载荷分布研究[J].中国电机工程学报,2013,33(11)：80～87.

[6]黄浙.风力发电机组变桨轴承结构强度设计[D].北京：华北电力大学,2014.

[7]朱琳，张钢，倪晓艇，等.风力发电机变桨轴承的力学性能分析[J].工业控制计算机，2015(28):106～112.

[8]丁伯民. ASME压力容器规范分析与应用[M].北京：化学工业出版社，2009.

[9]Liao N T,Lin J F.A New method for the analysis of deformation and load in a ball bearing with variable contact angle[J].Journal of Mechanical Design,2001，123:304～312.

[10]Damian J,Serna A. Design of four contact-point slewing for structural stiffness[J].Journal of Mechanical Design,2010，132:021006-1～10.

[11]冈本纯三.球轴承的设计计算[M].黄志强译.北京：机械工业出版社，2003.

[12]陈龙,赵联春,夏新涛,等.变桨轴承载荷分布分析[J].轴承,2010(1):1～4.

[13]李云峰,吴宗彦,卢秉恒,等.转盘轴承静载荷承载曲线的精确计算[J].机械设计与制造,2010(5):29～30.

[14]杨静,廖晖.风力机组偏航变桨轴承载荷分布分析及数值求解[J].东方汽轮机,2012(1):35～38.

[15]齐涛，董姝言，苏凤宇.MW级风机变桨轴承与轮毂连接螺栓的强度分析[J].机电工程，2014, 31(12)：1587～1652.

[16]张宏伟,扈文庄,邢振平,等.兆瓦级风电变桨轴承的技术要求与制造[J].轴承,2011(6):61～64.