基于改进蚁群算法的自动导引运输车全局路径规划方法研究*

梁建刚，刘晓平，王 刚，韩 松

(北京邮电大学 自动化学院，北京 100876)

0 引 言

由于具有运输效率高、人力成本低、安全可靠等诸多优点，自动导引运输车(AGV)成为当代物流自动化装备的重要组成部分[1]。AGV路径规划是指在具有一定障碍物的环境中，给定起始点和目标点，按照某些评价标准，在运行环境中搜索一条最优的无碰撞路径[2]。

传统的路径规划方法如人工势场法[3]、模拟退火算法[4]、模糊逻辑算法[5]等，普遍存在收敛速度慢、全局搜索能力差等缺陷。随着智能控制技术的发展，神经网络算法[6]、遗传算法[7]、蚁群算法等智能算法逐渐被应用于解决路径规划问题[8]。其中：神经网络算法具有自适应和自学习的能力，但是泛化能力差是其致命缺点；遗传算法适用于全局路径规划，但是搜索空间大、运算效率不高、运行速度慢；蚁群算法(ACO)由于具有启发性、并行性、强鲁棒性等特点，而受到研究人员的广泛关注。蚁群算法由意大利学者DORIGO M等[9]于1992年首先提出，是一种利用信息素正反馈的群智能算法，已经被应用于工程机械再制造选配[10]、遥感图像分类[11]、车辆交通系统等方面[12]。近年来，国内外学者从不同角度研究了蚁群算法在路径规划方面的应用问题。CHAARI I等[13]将遗传算法(GA)中的突变和交叉操作应用到蚁群算法中，设计了一种新的混合ACO-GA路径规划算法；GE B等[14]将蚁群算法每次迭代后的两条较短路径进行交叉组合产生新路径，并更新其信息素，加快信息素的正反馈效应，提高了算法的收敛速度；ZHANG C等[15]在路径规划过程中结合免疫抑制和参数切换策略，使算法准确性得到了提高；CHEN X等[16]基于气味渗透原理，提出了一种用于机器人路径规划的快速两阶段蚁群算法；GIGRAS Y等[17]提出了混合ACO-PSO算法用于机器人路径规划。

本研究提出一种基于改进蚁群算法的AGV全局路径规划方法。

1 AGV工作环境建模

路径规划问题包括环境建模和搜索算法两部分。常用的环境建模方法有可视图法、栅格法和MAKLINK图论法等。MAKLINK图论法又称为自由空间法，由HABIB M K和ASAMA H于1991年提出[18]。

为了简化问题，本研究在处理问题过程中，将AGV模型简化为点状机器人。利用MAKLINK图论法构建AGV运行环境模型，将环境中的障碍物依据AGV能无碰撞通过的最大尺寸进行膨胀化处理，转化为广义锥形或凸多边形等基本几何图形，将环境划分为障碍空间和自由空间，AGV运行环境模型如图1所示。

图1 AGV运行环境模型黑色区域—障碍空间；其余—自由空间

MAKLINK图论法中，不与障碍物相交的前提下，两个障碍物顶点之间的连线以及障碍物顶点到空间边界的垂线段称为MAKLINK线。初始时刻，取MAKLINK中点作为AGV的可行节点，连接各个MAKLINK线的中点及起始点S和目标点T，构成用于初始路径规划的无向网络图如图2所示。

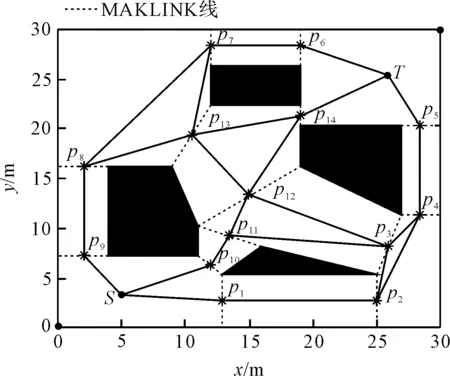
图2 无向网络图p1,p2,p3,...,p14—MAKLINK线

基于该环境模型，路径规划问题可以描述为：AGV从起始点S出发，避开空间中的障碍物，通过若干MAKLINK线，到达目标点T的最优路径问题。

2 改进蚁群算法

为了解决AGV路径规划的问题，本研究在起始点S循环释放人工蚂蚁，当蚂蚁到达目标点T时，通过在其经过的路径上添加信息素来引导其他蚂蚁的走向，循环多次，从而达到全局路径寻优的目的。

2.1 转移概率的改进

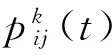
(1)

式中：J—从节点i出发所有可选路径节点j的集合；τij(t)—路径(i,j)的信息素浓度；ηij(t)—节点j的启发函数；α—信息素浓度τij(t)对转移概率的影响因子；β—启发函数ηij(t)对转移概率的影响因子。

启发函数ηij(t)的计算公式如下：

(2)

式中：dij—节点i与节点j之间的距离值。

dij值越小，节点j的启发函数值越大，节点j被选择的概率越大。

A*算法是一种典型的启发式搜索算法[19]，被广泛应用于路径规划领域。算法中引入评估路径节点n价值的估价函数f(n)，其计算公式如下：

f(n)=g(n)+h(n)

(3)

式中：g(n)—从起始点S到达节点n的实际行驶距离；h(n)—从节点n到达目标点T的预估行驶距离。

采用A*算法规划路径时，选择当前节点的邻居节点中估价函数f(n)值最小的点作为下一路径节点，使路径规划具有了目标导向性。

(4)

式中：djT—节点j与目标点T之间的直线距离，作为节点j距目标点的启发信息；wj—节点j距目标点的启发信息对路径规划影响的权重，wj∈[0,1]。

wj具体影响如下：

(1)wj=0。路径规划与节点j距目标点的启发信息无关，启发函数蜕化为传统蚁群算法的启发函数，算法收敛速度慢；

(2)wj是固定正值。当wj值较小时，算法搜索空间大，搜索侧重于广度优先，搜索的准确性提高，收敛速度慢，当wj值较大时，算法搜索空间小，搜索侧重于深度优先，搜索的准确性降低，收敛速度快；

(3)wj是动态值。可以实现不同阶段对搜索准确性及收敛速度快慢的动态需求。

wj的计算公式如下：

(5)

式中：Mmax—路径规划通过的MAKLINK线总数；Mcurrent—将依次经过的MAKLINK线以1为起始数值，按从小到大的次序逐个编号，该值为当前所处MAKLINK线编号值。

随着路径规划过程的进行，wj值逐渐增大，搜索前期侧重搜索的准确性，搜索后期侧重收敛的快速性。

将式(4)代入式(1)中，得到改进后的转移概率计算公式为：

(6)

2.2 变系数信息素更新策略

信息素更新包括实时信息素更新和路径信息素更新[20]。实时信息素更新是指蚂蚁每经过一个路径节点后即更新其信息素浓度：

τij(n+1)=(1-ρ)τij(n)+ρτ0

(7)

路径信息素更新是指蚁群完成一次搜索后，更新最优路径上每个节点的信息素浓度：

τij(n+1)=(1-ρ)τij(n)+ρΔτij

(8)

式中：τ0—信息素初始值；Δτij=Q/Lbest；Q—信息素浓度的常量；Lbest—本次搜索中最优路径长度；(1-ρ)—信息素的残留程度；ρ—信息素挥发系数，ρ∈[0,1]。

当ρ值较小时，信息素的残留程度较高，信息素正反馈作用相对较弱，算法搜索空间较大，搜索的随机性较强；当ρ值较大时，信息素的残留程度较低，信息素正反馈作用相对较强，搜索的随机性较低，算法收敛速度较快。

为了提高路径规划效率，采用动态调整信息素挥发系数策略。规划过程中，随着迭代次数的增加，逐渐增大信息素挥发系数ρ′，计算公式为：

(9)

式中：ρ0—信息素挥发系数初始值，ρ0∈[0,1]；Ncurrent—算法当前迭代次数；Nmax—算法最大迭代次数。

路径规划初始过程，由于信息素挥发系数较小，尽可能多的搜索到较优路径，降低了算法陷入局部最优的概率；随着迭代次数的增加，信息素挥发系数逐渐增大，算法收敛速度加快。将公式(9)代入式(7，8)得到改进后的实时信息素更新方法：

(10)

改进后的路径信息素更新方法如下：

τij(n+1)=(1-ρ′)τij(n)+ρ′Δτij

(11)

改进后蚁群算法流程图如图3所示。

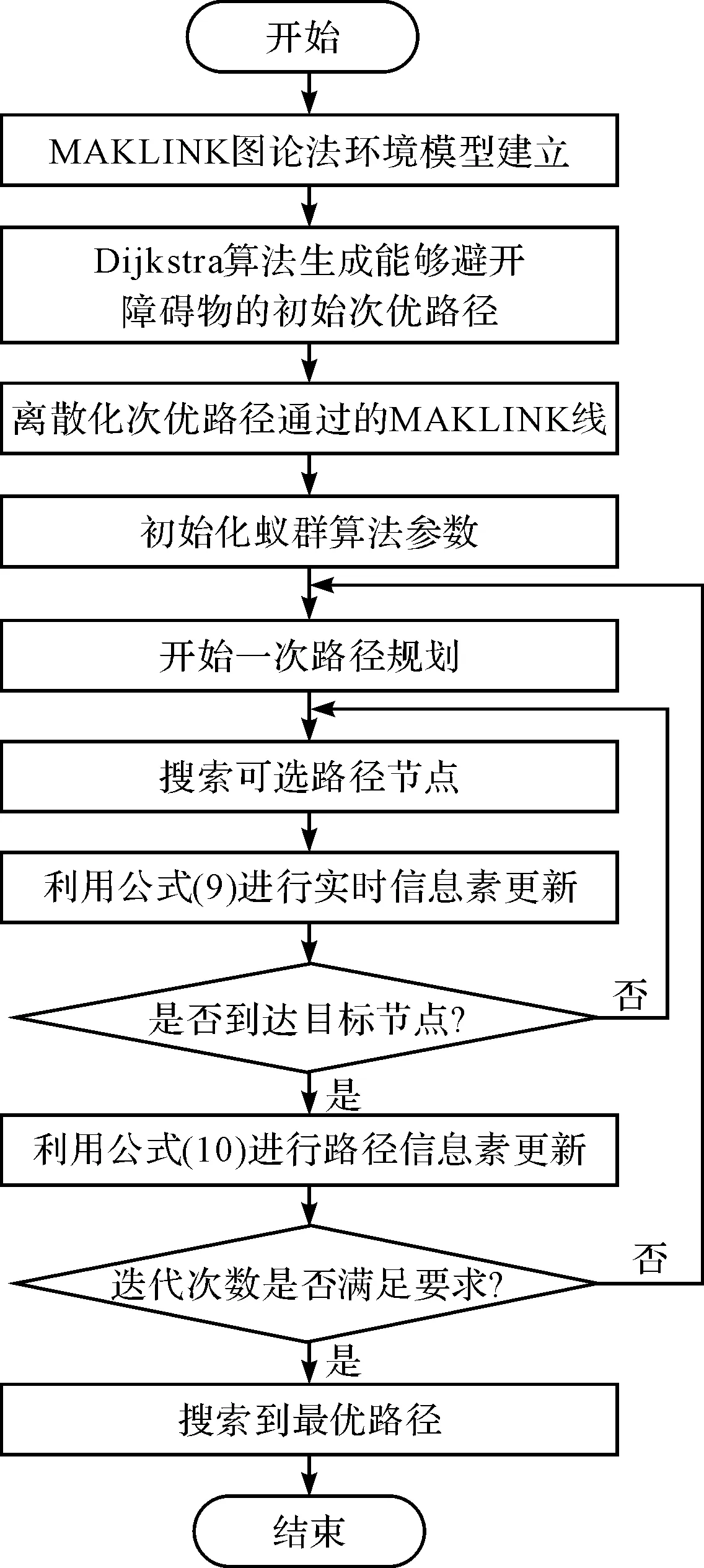
图3 改进后蚁群算法流程图

3 仿真实验和分析

为了验证改进蚁群算法在AGV全局路径规划中的有效性，笔者构建30 m×30 m的工厂环境模型，设定AGV起始点S坐标为(5,3)，目标点T坐标为(26,25)，定义4个多边形作为工厂中的障碍物。由Dijkstra算法规划出的初始路径经过的MAKLINK线依次为p10,p11,p12,p14，Mmax=4。笔者将p10,p11,p12,p14均等分为20段，等分点作为蚁群算法路径规划中AGV的可行节点。

蚁群算法中，设定信息素影响因子α=1，启发函数影响因子β=2，信息素浓度常数Q=6，信息素挥发系数初始值ρ0=0.1，种群中蚂蚁个数为10，算法最大迭代次数Nmax=200，信息素初始值τ0=0.000 3。

基于以上参数设置，传统蚁群算法和改进后蚁群算法搜索到的最优路径结果图如图4(a)、5(a)所示。收敛速度曲线如图4(b)、5(b)所示。

图4 传统蚁群算法路径规划仿真结果

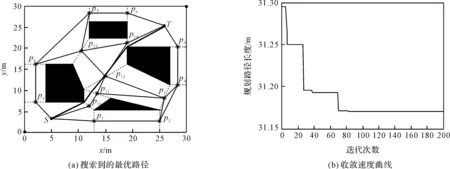
图5 改进后蚁群算法路径规划仿真结果

图中粗实线表示最优路径。从图中可知，传统蚁群算法在迭代次数达到110左右收敛到最优路径，而改进后蚁群算法在迭代次数为60左右就收敛到了最优路径，其收敛速度可达传统蚁群算法的2倍。

以上仅为一次仿真结果的对比，为消除偶然因素对算法的影响，参数设置同上，本研究对两种算法均独立进行50次路径规划实验。实验结果中，传统蚁群算法及改进蚁群算法的最优路径对比曲线如图6(a)所示。收敛速度对比曲线如图6(b)所示。

图6 传统及改进蚁群算法仿真结果对比曲线

根据50次路径规划仿真实验的结果，笔者计算最优路径平均值和收敛到最优路径的迭代次数平均值，计算结果如表1所示。

表1 传统蚁群算法与改进蚁群算法仿真结果对比

从表1实验数据对比可以看出：改进后蚁群算法搜索到的最优路径平均值为31.171 1 m，小于传统蚁群算法的31.172 0 m，说明改进后蚁群算法降低了搜索陷入局部最优的概率。改进后蚁群算法的迭代次数平均达58次时收敛到最优路径，而传统蚁群算法为107次，其收敛速度基本为传统蚁群算法的2倍，收敛速度显著提升。

4 结束语

针对AGV在工厂环境中进行快速路径规划，得到两点间最短距离的问题，本研究提出了基于改进蚁群算法的路径规划方法，该算法融合动态权重目标导向原理，增加了可选路径节点距目标点的启发信息，加快算法的收敛速度；信息素更新时，引入动态调整信息素挥发系数策略，随着路径规划的进行，逐渐增大信息素挥发系数，在前期降低陷入局部最优的概率，后期加快算法收敛速度，提高了路径规划效率。

通过仿真实验分析对比，证明了该算法在解决AGV路径规划问题时，具有更快的收敛速度、更高的规划效率。

参考文献(References):

[1] 李远仪，佃松宜，骆瑞森.基于便携式PC控制器的小型AGV系统[J].兵工自动化，2016，35(12)：26-29.

[2] 陈 杰.基于蚁群算法的机器人路径规划研究[D].南京：南京理工大学自动化学院,2009.

[4] MIAO H, TIAN Y C. Dynamic robot path planning using an enhanced simulated annealing approach[J].AppliedMathematics&Computation,2013,222(5):420-437.

[5] 李 擎,张 超,韩彩卫,等.动态环境下基于模糊逻辑算法的移动机器人路径规划[J].中南大学学报：自然科学版,2013,44(s2):104-108.

[6] LV Z, CAO J. Path planning methods of mobile robot based on new neural network[C]. Control Conference, Xi’ an: IEEE,2013.

[7] 王雪松,高 阳,程玉虎,等.知识引导遗传算法实现机器人路径规划[J].控制与决策,2009,24(7):1043-1049.

[8] 赵娟平,高宪文,符秀辉,等.移动机器人路径规划的改进蚁群优化算法[J].控制理论与应用,2011,28(4):457-461.

[9] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]. Ecal91-European Conference on Artificial Life, Paris: Elsevier Publishing,1991.

[10] 宿 彪,黄向明,任莹晖,等.基于蚁群算法的工程机械再制造优化选配方法研究[J].机械工程学报,2017,53(5):60-68.

[11] WANG M, WAN Y, YE Z, et al. Remote sensing image classification based on the optimal support vector machine and modified binary coded ant colony optimization algorithm[J].InformationSciences,2017,402(1):50-68.

[12] JABBARPOUR M R, MALAKOOTI H, NOOR R M, et al. Ant colony optimisation for vehicle traffic systems: applications and challenges[J].InternationalJournalofBio-InspiredComputation,2014,6(1):32-56.

[13] CHAARI I, KOUBAA A, TRIGUI S, et al. SmartPATH: an efficient hybrid ACO-GA algorithm for solving the global path planning problem of mobile robots[J].InternationalJournalofAdvancedRoboticSystems,2014,11(1):1.

[14] GE B, SHENG H. Ant colony optimization based on combined optimization for path planning[C]. International Conference on Logistics Engineering, Management and Computer Science, Paris: Atlantis Press,2015.

[15] ZHANG C, LI Q, CHEN P, et al. Ant colony optimization combined with immunosuppression and parameters switching strategy for solving path planning problem of landfill inspection robots[J].InternetionalJournalofAdvancedRobotrcSystems,2016,13(3):1.

[16] CHEN X, KONG Y, FANG X, et al. A fast two-stage ACO algorithm for robotic path planning[J].NeuralComputing&Applications,2013,22(2):313-319.

[17] GIGRAS Y, CHOUDHARY K, GUPTA K, et al. A hybrid ACO-PSO technique for path planning[C]. International Conference on Computing for Sustainable Global Development, New Delhi: IEEE,2015.

[18] HABIB M K, ASAMA H. Efficient method to generate collision free paths for an autonomous mobile robot based on new free space structuring approach[C]. IEEE/RSJ International Workshop on Intelligent Robots and Systems, Intelligence for Mechanical Systems, Osaka: IEEE,1991.

[19] 曲道奎,杜振军,徐殿国,等.移动机器人路径规划方法研究[J].机器人,2008,30(2):97-101.

[20] 郁 磊.Matlab智能算法30个案例分析[M].2版.北京：北京航空航天大学出版社,2015.