基于多尺度细观力学方法计算水泥基材料的导热系数

刘嘉涵， 徐世烺， 曾 强

(浙江大学 建筑工程学院， 浙江 杭州 310058)

水泥基复合材料是当今应用最广泛的建筑材料之一，而水泥基材料的导热系数是表征其导热能力大小的热学性能参数之一.在国家大力发展绿色建筑、提倡节能减排的大背景下，精确表征水泥基复合材料的导热系数，对该类材料的科学研究和工程应用具有重要意义.

国内外的相关研究[1-2]表明，影响水泥基材料导热系数的主要因素有骨料的种类、体积分数和混凝土的水灰比、饱和度等.国内外学者对水泥基材料导热系数的测试方法、影响因素和计算模型等开展了较多研究，但是这些方法本质上是纯经验的，自变量主要是混凝土配合比和骨料性质.由于水泥砂浆和骨料的导热系数离散性较小，水泥基材料可简化为由连续相水泥砂浆和分散相粗骨料组成的两相复合材料.目前，根据多孔多相材料模型建立的水泥基材料导热系数计算模型主要有以下几类：(1)不考虑界面热阻的串并联模型[3]、正方体分散相模型；(2)不 考虑界面热阻的Maxwell模型[4]及其推广模型Bruggeman模型[5]；(3)考虑界面热阻的Maxwell推广模型，如Hasselman-Johnson模型[6].但多数模型仍停留在单一尺度上，尽管计算得到的导热系数与试验结果较为吻合，但仍缺乏明确的物理意义.

多尺度方法是研究非均质材料的重要手段.在微观尺度上，水泥基材料可以视为由C-S-H凝胶、未水化水泥颗粒、孔隙及CH晶体等共同组成且具有一定微观结构的无机多孔材料；在细观尺度上，又可将其视为由水泥浆、砂粒及界面过渡区按照一定结构组成的复合材料.多尺度方法普遍用于复合材料的热学性能分析和力学性能分析[7-8].

本文基于Eshelby等效夹杂理论[9]和水泥基材料微观结构多尺度特征，利用Mori-Tanaka均质化方法，从细观力学的角度研究了水泥基复合材料的热力学性能，推导出了水泥基复合材料导热系数的一般表达式，并与参考文献中的试验值进行综合对比，以验证所提出模型的正确性和准确性.

1 模型建立

1.1 水泥基材料微观结构多尺度特征

随着水泥基材料表面测量技术的发展，多尺度概念被引入到水泥基复合材料的研究中，即在水泥基材料的不同尺度上建立相应的数学模型，分析材料的物理性能和化学性能，并通过一定的方法将水泥基材料的各个尺度相关联，从而系统掌握材料的本质.如Constantinides等[10]将水泥基复合材料的微观结构划分为4个尺度水平，如图1所示.图1包括：

图1 水泥基复合材料微观结构的4个尺度划分Fig.1 Four-level microstructure of cement-based composites[10]

(1)LevelⅠ，尺度为10-8～10-6m，此尺度上的物质目前被认为是C-S-H凝胶，由水泥基复合材料中的C2S，C3S水化得到.C-S-H凝胶包裹在未水化水泥颗粒外部.根据C-S-H凝胶微观结构的差异，可将其分为低密度C-S-H凝胶(LD)和高密度C-S-H凝胶(HD).

(2)LevelⅡ，尺度为10-6～10-4m，此尺度上的物质被认为是硬化水泥浆体，包含C-S-H凝胶、未水化的水泥熟料、毛细孔隙及CH晶体等.其中未水化的水泥熟料包括C2S，C3S，C3A，C4AF，毛细孔隙的性质与水胶比有关.

(3)Level Ⅲ，尺度为10-4～10-2m，此尺度上的物质主要为砂浆，是由水泥浆、细集料、界面过渡区(ITZ)组成的三相复合材料.

(4)Level Ⅳ，尺度为10-2～10-1m，此尺度上的物质被认为是由砂浆、粗骨料、ITZ组成的三相复合材料，即混凝土.

随着水泥基材料技术的不断发展，不同种类的新材料被逐渐应用到水泥基材料中来提高其性能.利用多尺度理论，可以灵活地将不同材料按照其尺度大小置于不同的尺度水平上，例如纳米材料可置于Level Ⅰ，粉煤灰(尺度为0.5×10-6～3×10-4m)可置于Level Ⅱ，玻化微珠(尺度为0.5×10-3～1×10-3m)可置于Level Ⅲ，从而完善水泥基材料热力学性能和力学性能的分析.

1.2 复合材料多尺度导热系数模型

根据Fourier定律，在导热现象中，单位时间内通过给定截面的热量正比于垂直于该截面方向上的温度变化率和截面面积，而热量传递的方向与温度升高的方向相反.用公式表示即为：

(1)

复合材料由多相组成，内部微观结构决定了材料的宏观性能，因此，可利用细观力学方法从材料的组分和微观结构来计算其宏观性能.假设在Level(i+1)和Leveli尺度上的导热系数分别为Khom(X)和Ki(x)，X和x分别为Level(i+1)和Leveli尺度上的位置向量.Leveli和Level(i+1)尺度上的温度梯度张量分别为：

(2)

通过平均Leveli尺度上的温度梯度和热通量张量可得到Level(i+1)尺度上的各张量为：

G=〈g〉V;Q=〈q〉V

(3)

根据平均场理论，利用一个二阶局部张量A(x)建立2个尺度的温度梯度线性关系，即：

g(x)=A(x)·G(x)

(4)

对于多相组成的不均匀材料，有：

〈g(x)〉Vs=〈A(x)〉Vs·G(x)

(5)

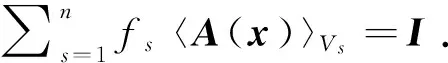
根据Fourier定律，有：

q(x)=Ki(x)·g(x)=Ki(x)·A(x)·G(X)

(6)

材料的整体导热系数可以表示为：

Khom(X)=〈Ki(x)·A(x)〉V

(7)

式(7)即为多相复合材料导热系数张量的一般表达式.二阶局部张量A(x)的表达式决定了Khom(X) 的最终值.本文使用Eshelby等效夹杂理论[9]来估计二阶局部张量A(x).Eshelby证明：设介质为线弹性，当无限大介质内的夹杂相形状为椭球形时，若本征应变是一个常张量，则特征应变也是一个常张量，且应变局部张量恒定.与弹性力学问题相似，与热传导有关的局部张量AT恒定.Hatta等[11]给出了AT的一般张量表达：

(8)

式中：S为Eshelby二阶张量；KM，KT分别为基质和夹杂相的导热系数张量；R为转换矩阵，用于将局部坐标系转换为整体坐标系.

对于多相复合材料，需要考虑夹杂相周围的导热系数K0，每一种夹杂相与热传导有关的局部张量As为：

(9)

式中:Ks,Ss分别为该相的Eshelby二阶张量和导热系数(s=1,2,3,…,n，n为相的个数).

根据Mori-Tanaka均质化方法[12]，将夹杂相周围的导热系数近似为材料基质的导热系数，即K0=KM，代入式(9)，则多相复合材料与热传导有关的局部张量As变为：

(10)

Eshelby二阶张量可以通过格林公式求得.当夹杂相为球体时，可以得到其Eshelby二阶张量为S=1/3trI.如果不考虑夹杂方向的影响，则转换矩阵R=I，代入式(10)，可得[13]：

(11)

将式(10)代入式(7)，并考虑式(11)，最终复合材料均匀化导热系数表达式为：

(12)

式中：fM，fs分别为基质和夹杂相的体积分数；n为夹杂相的个数；KM，Ks分别为基质和夹杂相的导热系数，W/(m·K).

当As=1时，该模型形式与并联模型表达形式一致；当As=KM/Ks时，该模型形式与串联模型表达形式一致；Benveniste等[14]证明，考虑热阻的Mori-Tanaka均质化导热系数与Hasselman-Johnson模型一致.这表明基于微观力学和Mori-Tanaka均质化方法的导热系数模型涵盖了一些经典导热系数的估算方法.

2 算例与模型验证

2.1 模型计算与水泥净浆试验结果比较

水泥净浆的多尺度模型可以简化为从LevelⅠ到levelⅡ两个尺度(见图1)，但在确定水泥净浆导热性能过程中需要做两次均质化处理.尽管水泥浆体材料成分非常复杂，但是已有一些普通硅酸盐水泥的基本水化反应规律和水化反应经典计算模型[15].需要注意的是，为了简化计算，本文将C3A，C4AF等物质等同于C3S和C-S-H来确定水泥净浆的导热系数范围(分别对应图2中Kmax和Kmin).其中C2S，C3S，CH，C-S-H的密度和导热系数分别为3.55，3.57，2.25，2.40g/cm3和3.45，3.35，1.32，0.98W/(m·K)[13].常温条件下，水的导热系数取为0.60W/(m·K).

图2(a)展示了不同水化程度(α)下的水泥净浆导热系数K与水灰比mw/mc之间的关系.可以看出，总体上，随着水化程度α的增加，水泥净浆整体的导热系数K逐渐减小.这主要是因为水化反应生成的C-S-H和CH的导热系数较小，这与文献[13]的计算结果一致.从图2(a)中还可以发现，增加水灰比将减小水泥净浆的导热系数，这一规律与Maruyama等[16]得到的试验结果相符，主要是因为水的导热系数远远低于C-S-H和其他固相的导热系数.图2(b) ～(d)分别对比了水灰比为0.348，0.30和0.40时在不同水化程度下的水泥净浆导热系数试验值[17-18]和计算值，其中计算值Kmax为将所有矿物组成等同于C3S的导热系数计算值，Kmin为将所有矿物组成等同于C-S-H的导热系数计算值.可以看出在水化反应初期，试验值更靠近Kmax；当水化反应进行到一定程度时，试验值更靠近Kmin，这表明其他矿物组成的导热系数更接近C3S的导热系数，而其他矿物组成水化产物的导热系数可能更接近C-S-H的导热系数.需要注意的是，图2(a)中的导热系数计算值均为平均值；另外，本文计算并没有考虑水自干燥导致材料的液相空间被导热系数更小的空气所代替的情况，因此可能导致模型高估了材料的导热系数.

图2 水泥净浆导热系数与水灰比和水化程度之间的关系曲线Fig.2 Plots of predicted thermal conductivity of cement pastes with different mw/mc against hydration degree[17-18]

图3对比了水灰比分别为0.25，0.30，0.35，0.40条件下水泥净浆导热系数的计算值和试验值,并且计算了试验值和计算值的相对误差，发现其范围在20%以内.试验配合比和具体参数见文献[19].从图3可以看出，水泥净浆在饱和状态下的导热系数明显高于其在干燥状态下的导热系数，这是因为水的导热系数显著高于空气的导热系数.由图3还可发现，对于干燥水泥净浆，随着水灰比的增大，导热系数计算值与试验值的误差逐渐增大，这可能是因为本模型不能完全考虑实际水泥浆体的微观结构和矿物分布随水灰比变化而发生的变化.研究结果还显示，在干燥状态下水泥净浆导热系数计算值与试验值的偏差较小，而在饱和状态下偏差较大.这可能是由于在饱水度较高的条件下，孔隙水的空间分布不符合Eshelby稀疏夹杂条件，从而导致Mori-Tanaka均质化方法偏差较大；另一方面，在饱水度较高的情况下，孔隙水可能形成热量传递的通路，从而导致饱和水泥净浆导热系数急剧增加.

2.2 模型计算与混凝土试验结果比较

混凝土的空间结构比水泥净浆复杂得多.基于多尺度特征，混凝土的导热系数按Level Ⅰ到level Ⅳ这4个尺度进行计算(见图1).根据上文得到的水泥净浆导热系数的计算值和文献[19-20]提供的数据，水泥净浆、石英、花岗岩、石灰岩的导热系数分别为1.094，4.450，2.500～2.650，2.290～2.780W/(m·K)；水泥、砂和碎石的密度分别为3.15，2.55，2.58g/cm3.在常温条件下，空气的导热系数为0.026W/(m·K).

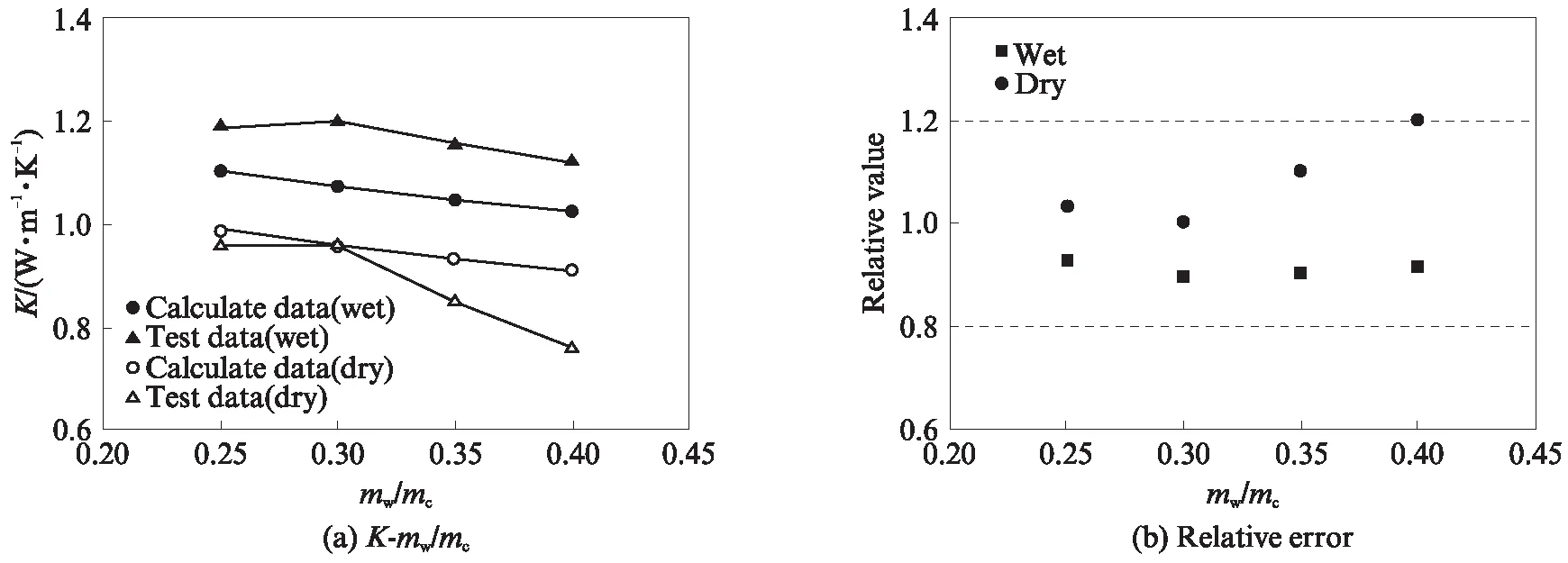
图3 不同水灰比下干燥和饱水水泥净浆导热系数试验值和计算值及其相对误差Fig.3 Predicted and measured thermal conductivity of dried and saturated cement pastes with different mw/mc, and the relative value between the predicted and measured thermal conductivity[19]

根据文献[19,21-22]提供的混凝土配合比和养护状态，采用本文提出的多尺度模型可计算得到不同粗骨料含量的混凝土导热系数.图4(a)将上述文献提供的试验值与本模型计算值的相对误差进行了比较.可以发现，本文提出的多尺度模型计算值与试验值的相对误差基本小于20%，说明本文提出的多尺度导热系数计算模型精度较高.这是因为本文提出的导热系数模型同时考虑了水泥净浆、细骨料和粗骨料在多尺度上对混凝土整体导热系数的影响，因此计算结果能够更好地与试验值吻合.

图4 干燥和饱水混凝土导热系数计算值与试验值的相对误差Fig.4 Relative errors between the measured and predicted thermal conductivity of dried and saturated concrete[19，21-22]

图4(b)列出了干燥和饱和条件下不同骨料含量混凝土导热系数计算值和试验值的相对误差.可以看出，本文提出的多尺度导热系数计算模型预测结果与试验值吻合度较高.在干燥状态下，导热系数计算值和试验值的偏差范围为1.4%～17.4%.其中，当骨料体积分数为49%～70%时，两者相对误差小于5%；随着骨料体积分数的降低，两者相对误差逐渐增加，当骨料体积分数为0%时，其相对误差达到了17.4%.注意到，在本文提出的多尺度模型计算过程中，水泥净浆的导热系数直接从纳米级别的C-S-H含量开始，并且将一些含量较低的矿物组成直接等价于C-S-H，从而造成了一定的误差.饱水状态下混凝土导热系数计算值和试验值的偏差范围为7.4%～14.3%，且误差值与骨料体积分数没有明显相关性.从图4(b)中还可以发现，采用本文提出的多尺度模型所得到的饱水混凝土导热系数计算值均小于试验值，这与图4(a)的结果类似.如前所述，这仍然是由于Mori-Tanaka均质化方法过于简化了孔隙水在水泥基材料中的空间分布和导热作用所致.

3 结论

(1)基于Eshelby等效夹杂理论和水泥基材料微观结构多尺度特征，利用Mori-Tanaka方法，从细观力学的角度研究了水泥基复合材料的热力学性能，推导出了水泥基复合材料的导热系数细观力学一般表达式.

(2)在饱和状态下，采用本文提出的多尺度模型计算水泥净浆导热系数所得到的结果精度较低；在干燥状态下，采用本文提出的多尺度模型计算得到的导热系数精度较高；随着水灰比逐渐增大，模型计算值与试验值之间的误差增大.

(3)本文提出的多尺度模型同时考虑了水泥净浆、细骨料和粗骨料在多尺度上对混凝土整体导热系数的影响，因此能够较好地预测混凝土导热系数.通过与串联模型、并联模型进行比较可知，本文提出的导热系数表达式精确度更高.

(4)本文提出的多尺度模型在计算饱水净浆和混凝土导热系数方面存在一定的误差，这可能是因为Eshelby稀疏夹杂条件和Mori-Tanaka均质化方法过于简化了水在孔隙中的空间分布和传热、换热作用所致.

参考文献：

[1] CAMPBELL-ALLEN D,THORNE C P.The thermal conductivity of concrete[J].Magazine of Concrete Research,1963,15(43):39-48.

[2] KHAN M I,BHATTACHARJEE B.Relationship between thermal conductivities of aggregate and concrete[C]//Civil Engineering Materials and Structures.India:Osmania University Hyderabad,1995:162-166.

[3] BART G C J.Thermal conduction in non homogeneous and phase change media[M].Delft:Delft University of Technology,1994:16-18.

[4] MAXWELL J C.A treatise on electricity and magnetism[M].Oxford,UK：Clarendon Press,1881:179-208.

[5] BRUGGEMANN D A G.The calculation of various physical constants of heterogeneous substances.I.The dielectric constants and conductivities of mixtures composed of isotropic substances[J].Annalen Der Physik,1935,24:636.

[6] HASSELMAN D P H,JOHNSON L F.Effective thermal conductivity of composites with interfacial thermal barrier resistance[J].Journal of Composite Materials,1987,21(6):508-515.

[7] TANG S,TANG C,LIANG Z,et al.Numerical study of the influence of material structure on effective thermal conductivity of concrete[J].Heat Transfer Engineering,2012,33(8):732-747.

[8] WEI S,YIQIANG C,YUNSHENG Z,et al.Characterization and simulation of microstructure and thermal properties of foamed concrete[J].Construction and Building Materials,2013,47:1278-1291.

[9] ESHELBY J D.The determination of the elastic field of an ellipsoidal inclusion,and related problems[C]//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.London,UK:The Royal Society,1957:376-396.

[10] CONSTANTINIDES G,ULM F J.The effect of two types CSH on the elasticity of cement-based materials:Results from nanoindentation and micromechanical modeling[J].Cement and Concrete Research,2004,34(1):67-80.

[11] HATTA H,TAYA M.Effective thermal conductivity of a misoriented short fiber composite[J].Journal of Applied Physics,1985,58(7):2478-2486.

[12] MORI T,TANAKA K.Average stress in matrix and average elastic energy of materials with misfitting inclusions[J].Acta Metallurgica,1973,21(5):571-574.

[13] QOMI M J A,ULM F J,PELLENQ R J M.Physical origins thermal properties of cement paste[J].Physical Review Applied,2015,3(6):064010.

[14] BENVENISTE Y,MILOH T.An exact solution for the effective thermal conductivity of cracked bodies with oriented elliptical cracks[J].Journal of Applied Physics,1989,66(1):176-180.

[15] TAYLOR H F W.Cement chemistry[M].London,UK:Thomas Telford,1997:191-196.

[16] MARUYAMA I,IGARASHI G.Cement reaction and resultant physical properties of cement paste[J].Journal of Advanced Concrete Technology,2014,12(6):200-213.

[17] MOUNANGA P,KHELIDJ A,BASTIAN G.Experimental study and modelling approaches for the thermal conductivity evolution of hydrating cement paste[J].Advances in Cement Research,2004,16(3):95-103.

[18] TANG S W,CHEN E,SHAO H Y,et al.A fractal approach to determine thermal conductivity in cement pastes[J].Construction and Building Materials,2015,74:73-82.

[19] KIM K H,JEON S E,KIM J K,et al.An experimental study on thermal conductivity of concrete[J].Cement and Concrete Research,2003,33(3):363-371.

[20] Japan Concrete Institute.The measuring methods of conductivity,diffusivity,and specific heat of concrete and their application[M].[s.l.]:Japan Concrete Institute Mass Concrete Division,1982:11-14.

[21] 张伟平,童菲,邢益善,等.混凝土导热系数的试验研究与预测模型[J].，2015,18(2)：184-189.

ZHANG Weiping,TONG Fei,XING Yishan,et al.Experimental study and prediction model of thermal conductivity of concrete[J].,2015,18(2):184-189.(in Chinese)

[22] van GEEM M G,GAJDA J,DOMBROWSKI K.Thermal properties of commercially available high-strength concretes[J].Cement,Concrete and Aggregates,1997,19(1):38-54.