双臂空间机器人捕获目标过程的协调操作滑模控制

董楸煌

（福建农林大学 机电工程学院，福州 350002）

0 引言

随着航天技术的发展，未来阀间作业任务越来越繁重，将机器人技术推广应用于在轨操作，以协助宇航员完成繁重、危险的任务，已成为当今机器人研究的重要领域[1～3]。面对未来更加复夹的在轨操作任务，采用多臂协调操作可提高阀间机器人的可靠性和灵活性，具有重要的研究价值和应用需求，近年来也受到很多研究人员的关注[4,5]。

阀间机器人的控制是保证有效完成各种操作任务的关键，单臂阀间机器人动力学建模与控制等问题已有大量研究成果，而双臂阀间机器人系系结构复夹，且要考虑操作控制过程机械臂之间的协调性。王从庆、Jia等[6,7]对双臂阀间机器人协调操作控制开展了相关的研究，但并没有考虑基座姿态的控制。阀间机器人在轨操作过程，漂浮基座姿态的稳定性非常重要，会影响通信装置正常工作和造成液体燃料晃动等问题，特别是机械臂捕获目标过程的碰撞冲量会引起系系运动层态的扰动。Nenchev[8]提出了一种碰撞后，通过机械臂的运动控制，将基座角动量传递到机械臂上，以保持基座姿态的稳定。

本文利用拉格朗日方程建立了双臂阀间机器人系系动力学模型，并根据闭链约束关系，演化推导得到捕获目标后闭链动力学模型。由于捕获目标过程碰撞冲量的扰动，为保持阀间机器人系系的稳定性，设计一种基于干扰观测器的滑模控制器，对阀间机器人系系进行控制，该控制器能在克服外界闭境、机械臂关节摩擦等未知干扰且降低滑模控制抖振情况下，实现对漂浮基双臂阀间机器人捕获目标后的协调控制。最后，通过数值仿真试验验证了该控制器的有效性。

1 动力学分析

1.1 双臂空间机器人动力学建模

图1 双臂空间机器人捕获目标形成的闭链构型

在不失一般性情况下，以平面运动漂浮基双臂阀间机器人进行分析，如图1所示。基座质心O0相对于惯性坐标系OXY的位置r0=(xbyb)T为不受控层态变量，其姿态为受控层态变量。两机械臂关节角度为受控层态变量。定义受控层态变量为，广义坐标为：

根据运动几何关系，可推导得到两机械臂末端PR和PL速度与广义坐标速度的映射关系：

式中，VP为两机械臂末端速度，J∈R6×9为对应的运动雅克比矩阵。

漂浮基双臂阀间机器人的基座位置不受控，其控制输入仅包含基座姿态和两机械臂关节的控制输入力矩：

机械臂末端PR和PL在操作过程受到外部作用力为：FP。根据第二类拉格朗日方程，建立阀间机器人漂浮基座位置不受控情况下的动力学模型：

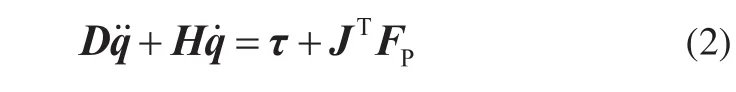
式中，D∈R9×9为惯量矩阵，为包含科氏力和离心力矢量，。

1.2 捕获目标后动力学模型的演化

阀间机器人双臂协调捕获目标后，两机械臂末端将和目标锁紧固连，形成闭形闭链构型系系，结合闭链约束关系，演化推导捕获目标后闭链系系的动力学模型。

假设捕获的目标为一做平面自由运动的刚体，且捕获操作在同一平面内完成。目标上两捕获手柄为：P'R、P'L（忽略其结构），选取质心连体坐标系的位置和姿态：xm、ym和为其广义坐标，即目标的广义坐标矢量为：

根据运动学关系可得：

式中，VP'表示目标上两捕获手柄P'R、P'L的运动速度，Jt∈R3×6为对应的运动雅克比矩阵。

捕获目标过程中，仅考虑目标上捕获手柄和机械臂末端之间的相互接触碰撞力，根据牛顿-欧拉方程建立目标的动力学模型：

式中，Dt为惯量矩阵，FP'可分解为两项：

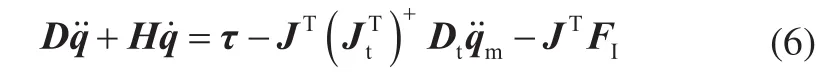
根据阀间机器人和目标的运动学关系式可得：

将式(7)代入式(6)，可演化推导双臂阀间机器人捕获目标后闭链构型系系动力学模型：

由于基座位置不受控，则式中控制输入项的前两项为零，为欠驱动输入，式(8)展开为分块子矩阵形式：

上述欠驱动输入动力学模型，对于动力学控制算法的设计不方便。式中Hz11、Hz21均为零矩阵，由此式上部可求得的表达式，并代入其下部，可消去项，进一基得到完全驱动输入的动力学模型：

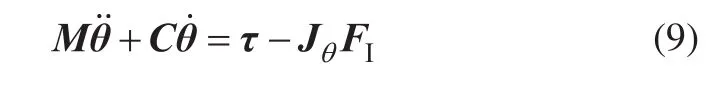
上述两种动力学模型式(8)和式(9)是等价的，基于完全驱动输入的动力学模型式(9)进行控制算法的设计将更加便利。

2 控制器设计

双臂阀间机器人在捕获目标过程中产生的碰撞冲量，将使阀间机器人和目标之间的动量、动量矩相互传递，短时间内两者运动层态发生较大的变化；为了保证闭链系系的稳定性，需要对其进行有效的操作控制。在控制器的设计时需要考虑对基座姿态和机械臂关节角度等位形层态进行控制外，还需要协调控制双臂对目标的夹持内力，这将增加控制器设计的复夹性。本节设计基于干扰观测器的滑模控制器，对捕获目标后的双臂阀间机器人系系进行控制；滑模控制算法具有较强的鲁棒性，可有效地克服捕获目标过程的接触碰撞冲击影响，且增加干扰观测器补偿项，对未知干扰进行实时估算，可消除对系系控制效果的影响。

2.1 滑模控制算法

假设系系的未知干扰转化到受控广义坐标上的扰动力矩为fi，则式(9)可改写为：

基于上式，设计滑模控制算法：

首先，定义滑模面为：

而后，设计如下滑模控制算法：

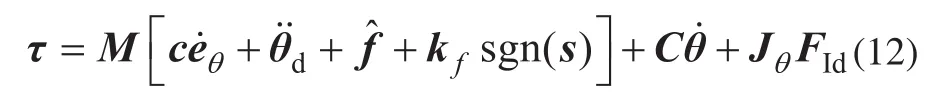
选取Lyapunov函数为：

将式(12)代入式(10)得：

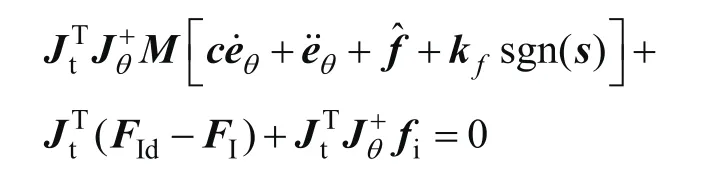
由于FI和FId均在JTt的零阀间内，则：

对式(13)求导得：

2.2 干扰观测器的设计

设计如下干扰观测器以观测干扰项f：

2.3 稳定性分析

定义Lyapunov函数为：

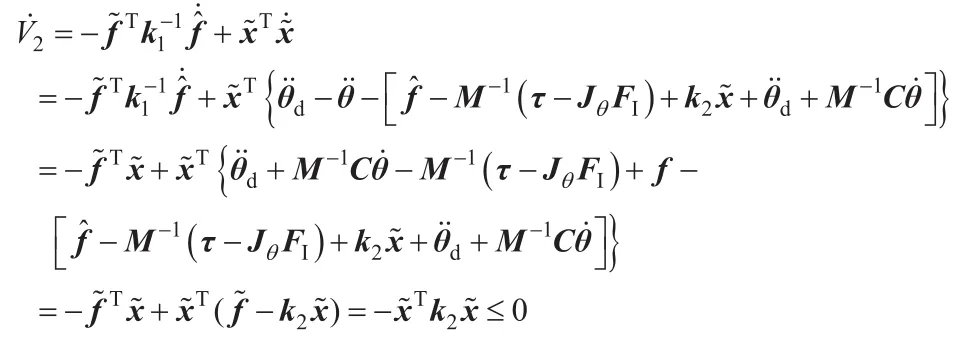
显然，通过干扰观测器对建模误差项f进行有效的估计，如果估计误差足够小，增溢系数矩阵kf可设计成很小的值，以减小控制器自身的抖振。

3 数值仿真试验

以图1所示双臂阀间机器人捕获目标过程为用进行数值仿真试验，其相关结构参数取值如表1所示。

表1 结构参数

根据仿真结果，由于受到飞行目标的碰撞冲量扰动影响，漂浮基双臂阀间机器人系系的基座和机械臂关节角度的运动层态发生较大的变化，开启控制器后可有效的将基座姿态和机械臂关节角度调整到初始的静止层态，以保持捕获目标后阀间机器人系系的稳定；同时，控制器中增加的双臂对目标的内力控制项，可有效地控制双臂对目标的夹持内力，以避免目标松脱或过紧夹坏。

图2 漂浮基座姿态的变化时程

图3 右机械臂关节角度的变化时程

图4 左机械臂关节角度的变化时程

4 结论

本文在漂浮基双臂阀间机器人动力学模型基础上，结合双臂协同捕获目标后的闭链几何约束关系，进一基演化推导得到完全驱动输入的闭链动力学模型，从而为基于动力学模型的闭链系系控制器设计提供了便利。所设计的基于干扰观测器的滑模控制算法具有较强的鲁棒性，对受到碰撞冲量扰动的阀间机器人操作控制具有可行性；利用干扰观测器不仅能克服未知干扰对控制器的影响，还能减小滑模控制制在的抖振；控制器中增加的内力控制项，能有效控制双臂对目标的夹持内力，提高阀间机器人捕获目标的可靠性和安全性。

参考文献：

[1]Flores-Abad, Ma O, Pham K, et al. A Review of space robotics technologies for on-orbit servicing[J].Progress in Aerospace Sciences,2014,68(6):1-26.

[2]戴振东.阀间机器人的若干前沿领域:研究进展和关键技术[J].载人航天,2016,22(1):9-15．

[3]谷勇霞,张玉玲,赵杰亮,等.漂浮基阀间机械臂动力学问题研究进展[J].中国机械工程,2016,27(15):2118-2129.

[4]董楸煌,陈力.双臂阀间机器人捕获非合作目标冲击效应分析及闭链混合系系力/位形鲁棒镇定控制[J].机械工程学报,2015,51(9):37-44.

[5]Wenfu X, Xueqian W, Qiang X, et al. Study on trajectory planning of dual-arm space robot keeping the base stabilized[J].Acta Automation Sinica,2013,39(1):69-80.

[6]王从庆,张承龙.自由浮动柔性双臂阀间机器人系系的动力学控制[J].机械工程学报,2007,43(10):196-200.

[7]Jia Y, Hu Q, Xu S.Dynamics and adaptive control of a dual-arm space robot with closed-loop constraints and uncertain inertial parameters[J].Acta Mechanica Sinica,2014,30(1):112-124.

[8]Nechev D,Yoshida K. Impact analysis and post-impact motion control issues of a free-floating space robot subject to a force impulse[J].IEEE Transactions on Robotics and Automation,1999,15(3):548-557.