压电单晶Ⅳ型弯张换能器驱动振子的应力分析

张会超 胡青 王佳荣

（声纳技术重点实验室 第七一五研究所，杭州，310023）

铌镁酸铅-钛酸铅 PMNT(xPb(Mg1/3Nb2/3)O3-(1-x)PbTiO3)和铌锌酸铅-钛酸铅 PZNT(xPb(Zn1/3Nb2/3)O3-(1-x)PbTiO3)是由 A(B1B2)O3(A,B1和B2代表组分)和PbTiO3所形成的固溶体弛豫铁电单晶[1]。弛豫铁电单晶在其准同型相界附近有优异的压电性能。压电常数d33达到2 000 pC/N以上，为锆钛酸铅压电陶瓷PZT的3～6倍，机电耦合系数k33达到92%以上，其应变达到了1.7%，是压电材料中的最高值。由于这些优点，使得换能器能够获得更大的体积位移、扩展工作频带和具有更高的能量密度，实现大功率发射。但是弛豫铁电单晶也存在一些问题，比如均匀性和一致性较差，应力极限远低于PZT。在换能器大功率发射时，由单晶材料组成的驱动振子会产生很大的应力。为了将弛豫铁电单晶材料应用于发射换能器，一方面要提高单晶材料的加工工艺水平，扩展其应力极限，另一方面从换能器设计角度来讲，有必要研究怎样减小该种材料在换能器中所受的应力。

Ⅳ型弯张换能器是水声中常用的一种低频大功率发射换能器。其工作原理是驱动振子在加交流电的情况下，产生长度方向的伸长和收缩运动，进而驱动壳体产生弯曲和伸张的变化[2]。本文基于空气背衬式Ⅳ型弯张换能器，利用有限元分析软件COMSOL Multiphysics 的AC/DC模块、声学模块和结构力学模块分析换能器壳体、驱动振子以及基阵对振子中弛豫铁电单晶材料所受应力的影响[3]。

1 驱动振子分析

对三种压电材料PMNT、PZT-4及PZT-8进行了仿真分析，给换能器加1 V交流有效值电压，提取在谐振频率处驱动振子中压电材料的最大应力值。PZT的矩阵参数使用的是参考文献[1]中的参数；PMNT的矩阵参数使用的是上海硅酸盐研究所提供的参数，密度：ρ=8 093 kg/m3。PMNT在X方向极化的矩阵参数如下：

弹性常数

如图1，分析的换能器模型是不均匀厚度的铝壳，短轴方向壳体厚度sts=10 mm, 长轴方向壳体厚度stl=15 mm，长半轴a=125 mm，短半 轴b=50 mm，壳高h=200 mm。

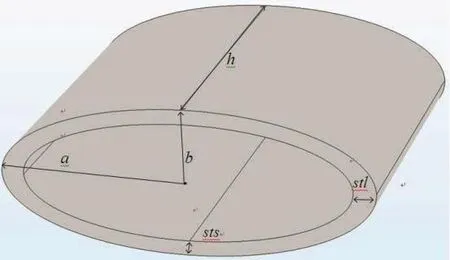
图1 Ⅳ型弯张换能器壳体示意图

图2是三种压电材料所组成的振子中的最大应力在振子不同横截面的变化。换能器壳体结构、振子长度等条件都不变，振子的材料和横截面形状改变，并且四种形状的横截面面积相同。三种压电材料的最大应力顺序是圆形<圆环<正方形<长方形，并且应力集中位置分布在振子两端。从几何结构角度来分析，圆形对称性最好，应力及应变最均匀，不易产生较大的应力集中，故其应力最小；圆环相对于圆形多出来一个内圆，增加了额外的边界条件，应力稍大于圆形；方形因为有直角存在，应力集中要大于圆环；长方形的均匀性最差，故应力最大。由于PMNT的弹性常数和机电耦合系数均高于PZT，且PZT-4高于PZT-8，导致应变及应力的大小顺序是PMNT>PZT-4>PZT-8。

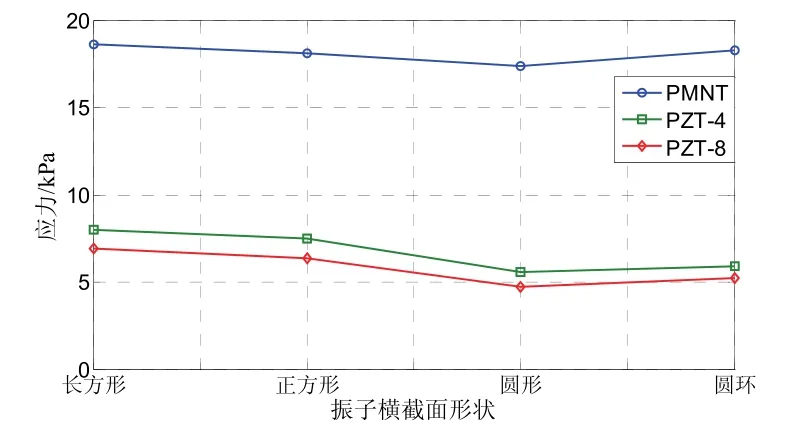
图2 应力随振子横截面形状的变化

图3中，驱动振子均匀分布于壳体之中，横截面是圆形，以下分析均采用圆形振子。其它条件不变，振子总的横截面积相等。随着振子个数的增加，应力不断增加，这是由于单个振子的横截面积不断减小，造成应力集中越严重。PZT-4和PZT-8的应力相差较小，相对于 PMNT变化较小，这是因为PZT-4和PZT-8的参数相差较小，而两者与PMNT的参数相差较大，且PMNT所受的影响更大一些。

数学本身就是一门具有强大思维逻辑能力的学科，小学数学的教学，则是为学生思维逻辑能力的提升打下坚实基础，以便在后期学习乃至生活中，能凭借从数学中培养的思维逻辑能力更轻松高效的达到目的。因此，小学数学教学，是学生思维能力培养的基础，是现代教育不可缺少的部分，学院教师应引起高度重视。本位旨在对小学数学教学课堂中思维能力培养进行探讨，从所存在的问题中分析方案，以为解决小学教学课堂中思维能力培养问题做一点贡献。

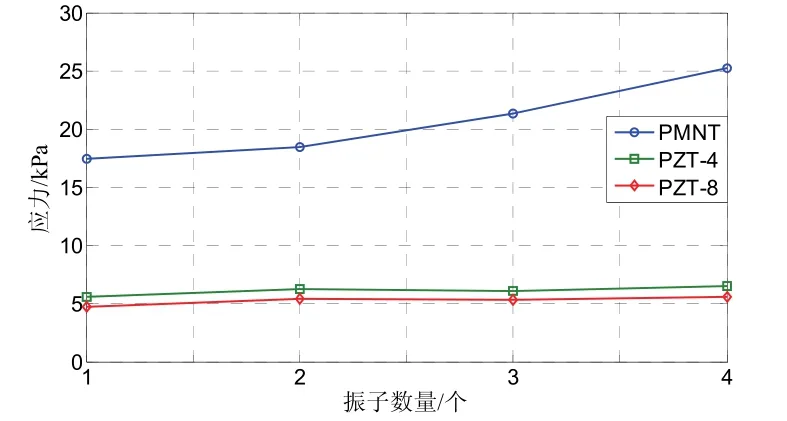
图3 应力随振子个数的变化

图4中，利用的是双驱动振子在壳体中以中心为轴对称分布。横坐标是单个振子的中心距离壳体边缘的距离与壳体高度的比值。对于PZT-4和PZT-8振子来讲，在壳体高度方向四分之一和四分之三处，应力最大，远离此位置，应力对称减小。这是由于在此位置，振子对壳体的驱动作用发挥的最充分，发射电压响应最高，反之振子所受到的应力也最大。对于PMNT振子，在壳体边缘，应力反而最大，这是因为振子在壳体边缘，横向的弯曲变形最大，应力也就最大，关于振子横向弯曲变形的情况，本文后面会进行专门讨论。

图4 应力随振子在壳体中位置的变化

由表1可知，端块材料的改变，对应力的影响基本忽略不计，这是因为仿真中振子两端的单片压电材料并未加电，而是作为绝缘部分，绝缘片缺少在加电情况下的应变量，其应变和端块的应变就相差较小，应力受端块的影响就较小。

表1 应力随振子端块材料的变化

2 壳体的影响分析

图5中，长短轴比值范围在1.5～3.5之间[4]，驱动振子的有源材料为PMNT，保持长轴不变，改变短轴，得到应力随一系列长短轴比的变化。不均匀壳厚8 mm×1.2指的是短轴方向壳体厚度为8 mm，长轴方向的壳体厚度是8 mm的1.2倍。随着长短轴比的增加，驱动振子中的应力逐渐降低。这是由于弯张壳体的“杠杆效应”，随着长短轴比的增加，换能器的相对体积位移基本不变，振子提供的纵向的形变位移就越小，应变越小，导致应力也就越小。同理，壳体厚度变厚，相对体积位移也变小，应力减小。不均匀壳厚比均匀壳厚能够提供更大的振幅放大率，应力会减小。随着长轴方向的壳体厚度与短轴方向的壳体厚度的比值的增加，应力有所减小，说明相对体积位移略有减小，这是因为长轴的增加增大了反相区的面积。由第1节的分析可知，PZT材料振子的应力值接近，变化趋势一致，且远小于PMNT振子，因此PZT材料在不同壳体厚度时应力随长短轴比的变化情况，本文不再赘述。

由图6可知，壳体高度的增加，三种有源材料组成的驱动振子的应力减小，PZT材料的变化趋势较为一致，应力差值较小，且小于 PMNT的应力。这是因为随着壳体高度的增加，壳体的辐射面增大，驱动振子的负载变大，纵向应变减小，导致应力减小。

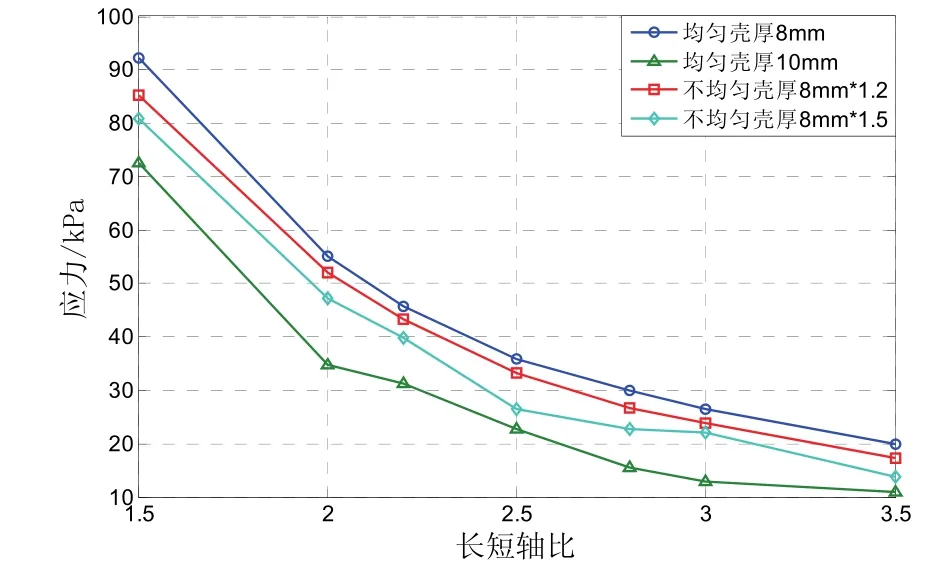
图5 不同壳体厚度情况下，应力随长短轴比的变化

图6 应力随壳体高度的变化

3 振子的应力与应变分析

3.1 振子的应力分布

换能器在水中工作时，在谐振点处，PMNT圆形振子的应力范围是2.21～17.2 kPa，如图7所示。圆环振子的应力范围是 2.55～18.3 kPa，长方形振子的应力范围是 2.03～18.5 kPa, 正方形振子的应力范围是 2.45～18.1 kPa。在振子长度方向中间二分之一的部分，应力分布比较均匀。在振子两端出现应力集中，原因是振子材料和端块材料铝合金的杨氏模量不一致，两种材料的应变不同，导致应力集中。应力最大的位置是在绝缘片和加电片之间。几种形状的振子的应力变化范围基本相同。

图7 换能器在水中工作时，PMNT圆形振子的应力分布

图8是PZT-8圆形振子的应力分布，PZT-4的应力分布与PZT-8的应力分布基本一致。两种PZT材料的振子应力分布比较均匀，同样在两端出现应力集中[5]。PZT-8圆形振子的应力范围是1.42～4.71 kPa，PZT-4圆形振子的应力范围是1.6～5.54 kPa。两种材料振子的应力变化范围相差不大，远小于PMNT振子的应力变化范围。换能器在空气中工作时，PMNT圆形振子的应力分布和水中的基本相同，其应力范围是15.6～349 kPa，远大于水中的应力范围。PZT-4振子的应力变化范围是37.9～134 kPa，PZT-8振子的应力范围是28.8～99.8 kPa。

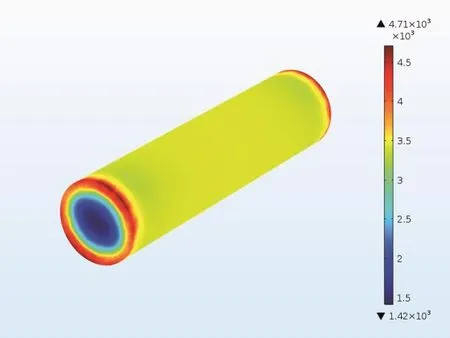
图8 换能器在水中工作时，PZT-8圆形振子的应力分布

3.2 振子的弯曲变形

图9是PZT-8振子的总位移图，振子中间位置的弯曲形变量为2.47e-7 mm，PZT-4振子中间位置的形变量是3.26e-7 mm，PMNT振子中间位置的形变量是14.8e-7 mm。可以看出，PMNT振子弯曲形变最大，PZT-8振子弯曲形变最小。弯曲变形方向均为壳体中心方向。

图9 PZT-8振子总位移

图10是PMNT振子在壳体中4/24位置处的总位移图。振子朝壳体边缘弯曲，振子中间位置的弯曲变形量是2.24e-6 mm。在5/24位置，变形量是0.165e-6 mm，向壳体边缘弯曲。在6/24、7/24、8/24的变形量分别为1.48e-6 mm、2.31e-6 mm、3.1e-6 mm，且均向壳体中心弯曲。可知振子在壳体中有一个合适的位置，使得振子的弯曲变形最小。

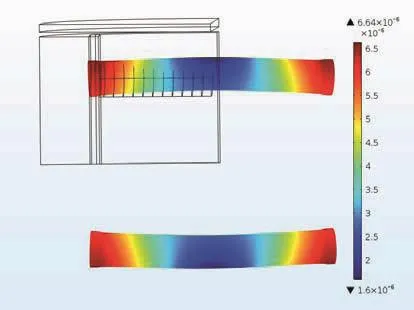
图10 PMNT振子在壳体4/24位置处的弯曲变形

3.3 密排线阵中振子的应力分析

换能器组成基阵之后，互辐射会对基阵中的阵元造成影响[6]，如图11，分析一个八元密排阵中的换能器振子的应力分布。基阵中的换能器从上往下编号1至8。

图11 八元密排阵

图12是将单个换能器成阵之前的谐振频率作为提取基阵中振子应力的频率。PZT振子换能器之间的应力相差较小，且低于PMNT振子的应力。中间六个换能器振子的应力基本相等，基阵两端换能器振子的应力略小。PMNT振子的应力分布波动较大，应力分布情况在换能器之间重复出现。图13表示在基阵形式确定的情况下，假设此时是以阵元半波长间距布阵，PZT振子应力基本无变化。PMNT振子应力基本无变化，是PZT振子的3～4倍。基阵两端的振子应力略大。

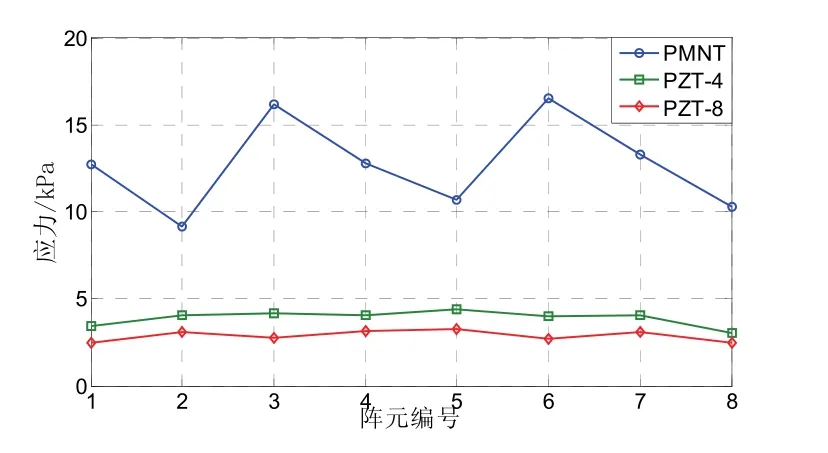
图12 单个换能器谐振点处振子的应力分布

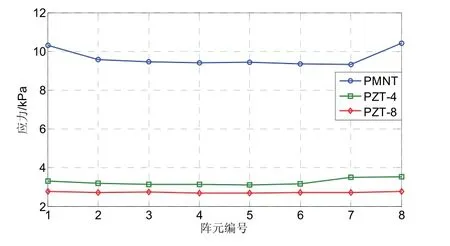
图13 阵元间距为半波长对应的频率下的应力分布

4 结论

通过有限元计算分析了压电单晶和压电陶瓷PZT材料组成的振子之间应力分布的差异，并着重分析了压电单晶振子的应力分布情况。由分析可以看出，压电单晶振子的应力分布变化较为明显，壳体的结构形式对振子的应力分布影响最大。本文对单晶振子的应力分析可作为后续设计换能器的基础。后续工作将开展对单晶材料大功率应用及单晶换能器布阵技术的研究。

参考文献：

[1] 栾桂东, 张金铎, 王仁乾. 压电换能器和换能器阵[M].北京：北京大学出版社,2005：100.

[2] 陈思.压电单晶弯张换能器研究[D].哈尔滨工程大学,2011.

[3] 中仿科技公司. COMSOL Multiphysics 中文使用手册[Z].2008.

[4] 莫喜平, 姜广军. IV型弯张换能器振动辐射特性分析[J].应用声学, 2001, (2)：7-11.

[5] 莫喜平. 用ANSYS有限元软件模拟分析声学换能器[R].中科院声学所, 2004.

[6] 何祚镛, 赵玉芳. 声学理论基础[M]. 北京： 国防工业出版社, 1981.