基于PCA-Fisher最优分割法的汛期分期影响研究

唐 莉，张永波，祝雪萍，王权威

(太原理工大学水利科学与工程学院，山西太原030024)

0 引 言

实际工作中，分期设计洪水与分期调整汛限水位的基础是合理的确定汛期分期。汛期分期对流域、水库防洪及洪水的安全利用等具有重大意义[1]。汛期因具有随机性、确定性、模糊性等变化规律[2]，针对其特点的现行分期方法主要有[3]：成因分析法、模糊集法、系统聚类法、分形法等；但这些方法或只能处理单指标的聚类问题，或不能考虑样本时序性。而Fisher分割法既维持了样本时序性，又能综合考虑多种指标，并能划定最优分类数目，对汛期分期具有较高的适用性[4-5]；然而，以往在运用Fisher分割法汛期分期时，依据经验确定汛期的研究域，不够客观[6]；为此本文以申村水库为例，应用均值变点分析法寻找月降雨径流的相关系数列变点，定量确定汛期研究域，再分别以旬与候为研究论域，采用主成分分析法(PCA，principal component analysis)[7]确定各指标的权重，克服Fisher最优分割法视各指标等权重的不足，称之为PCA-Fisher最优分割法。

1 方法理论

1.1 Fisher最优分割法

Fisher最优分割法是以样本各类间的差异最大，各类内部的差异最小为原则，对一列有序样本进行分割。汛期分期属于聚类分析，而聚类分析又分为有序样本与非有序样本两种。Fisher最优分割法作为有序样本的聚类方法，其最优解是使分成各组总的离差平方和最小；而所有可能的分类中都保持了样本的时间连续性。正是该特性使其能够保持样本的时间连续性。具体分割步骤参见文献[5]。

1.2 均值变点分析

王贺佳等提出：汛期的开始时间是雨量由少到多的时刻，会存在变点；而汛期的结束时刻是雨量由多到少的时刻，也会存在变点[8]。相似地可以得到：汛期的开始时间是降雨-径流相关系数由低到高的时刻，在这个时刻会存在“变点”，而汛期的结束时刻则是降雨-径流相关系数由高到低的时刻，同样在这一时刻也会存在变点。可以从寻找非汛期与汛期转化为寻找降雨-径流相关系数强度的变点的变点。变点指的是有序数列在某一时刻突然发生变化，这一时刻便称为变点。本次采用均值变点分析法来寻找变点，然后根据变点进行分期，均值变点分析的步骤如下：

对有序相关系数数列{λθ}(θ=1，2，…，12)，因为汛期的开始时刻与结束时刻分别在相关系数最大所对应月前后，所以按照数列中最大的相关系数把有月相关系数数列划分为两列。即，λ1，λ2，…，λt和λt，λt+1，…，λ12，其中λt=max(λ1，λ2，…，λ12)。

假定有序月相关系数数列λ1，λ2，…，λ12在第θ个月与第θ+1个月处断开，则可计算统计量

(5)

(6)

β=D-Dt

(7)

最大β值对应的第θ个月为变点，从而可以求出汛期开始的月；同理，对有序数列λt，λt+1，…，λ12进行上述演算，也就可以得到汛期结束的月。根据汛期开始与结束的月，可以对汛期与非汛期进行划分。

2 实例分析

申村水库位于山西省长治市长子县南陈乡申村，属浊漳河南源控住流域，是具有防洪、灌溉、生态旅游、供水综合利用功能的年调节中型水库。该流域属大陆山区性气候，夏季温湿，冬季干冷，多年平均气温9.6 ℃，极端最高气温37 ℃，极端最低气温-27 ℃，平均风速1.9 m/s，最大风速27 m/s，最大冻土深66 cm，多年平均降水量637.1 mm(1962年)。最大年降水量1 028.3 mm(1962年)，最小年降水量398 mm(1965年)。

2.1 研究期确定

本文统计分析了申村水库1981年～2010年共21 a的月降雨-径流资料，得到了降雨P和径流R的平均相关系数矩阵X。

以最大相关系数为端点，将有序相关系数数列划分为两列。即1月到8月和8月到12月。对于1月到8月对应的相关系数数列，分别使用式(5)～(7)计算β。图1为β在设定不同的断开情况下的变化。

图1 1月～8月 β随 θ的变化

由图1可知，变点为第5个月为变点，即5月为断开处。同理，对于8月到12月对应的有序相关系数数列，可得到第2个变点，即10月为断开处，得出5月到10月为申村水库汛期。

2.1.1 样本指标选取及指标权重计算

在初步拟定的5月～10月为汛期的研究时段中，以旬为基本单位，将整个研究时段划分为18个旬。以申村水库1980年～2010年共31 a的逐日降雨、径流资料为基础，取能反映水库控制流域汛期内暴雨洪水变化特征的暴雨指标：多年旬平均雨量、旬最大1 d雨量、暴雨天数(日降雨量大于25 mm)、旬最大3 d雨量等7个因子作为影响因子。洪水指标选取：多年旬平均入库流量、旬最大1 d洪量、旬最大3 d洪量等。运用SPSS软件对标准化的样本数据进行主成分分析，得各指标的权重ω=(ω1，ω2，ω3，ω4，ω5，ω6，ω7)=(0.315，0.289，0.077，0.061，0.105，0.091，0.601)。

表1 F(n，k)计算结果

2.1.2 分期计算

由于各指标间的单位不同，需先将各指标进行无量纲化处理；再利用上面求得各指标的权重系数，对无量纲化的结果求加权平均值；最后计算得出初始分类样本向量Y。即：Y=[0.27 0.31 0.32 0.50 0.30 0.41 0.44 0.42 0.80 0.64 0.58 0.66 0.49 0.50 0.46 0.25 0.52 0.25]T；再计算各截断样本的目标函数F(n，k)值，结果见表1。

绘制目标函数F(n，k)-k和非负斜率β(k)-k曲线如图2所示。从图2可看出，在k=3处F(n，k)-k曲线最陡并出现拐弯，且β(k)-k曲线，k=3时取值最大，所以可确最优定分类数k=3。从表1则可以得出分为{1，2，3，4，5，6，7}{8，9，10，11，12}和{13，14，15，16，17，18}三类，即5月1日到7月10日为前汛期，7月11日到8月30日为主汛期，8月31日到10月30日为后汛期。

图2 F(n，k)-k和 β(k)-k曲线

2.2 暴雨因素分析

2.2.1 样本指标选取及指标权重计算

在拟定的5月～10月为汛期的研究时段中，以旬为基本单位，将整个研究时段划分为18个旬。选取综合指标中4个暴雨指标作为影响因子，运用SPSS软件对标准化的样本数据进行主成分分析，得各指标的权重ω=(ω1，ω2，ω3，ω4)=(0.316，0.401，0.196，0.086)。

2.2.2 分期计算

由于各指标间的单位不同，首先要将各指标进行无量纲化处理；再利用上面求得各指标的权重系数，对无量纲化的结果求加权平均值；最后计算得出初始分类样本向量Y=[0.38 0.36 0.39 0.49 0.42 0.74 0.64 0.59 0.93 0.47 0.71 0.74 0.39 0.55 0.33 0.23 0.31 0.12]T；再计算各截断样本的目标函数F(n，k)值，绘制目标函数F(n，k)-k和非负斜率β(k)-k曲线如图3所示。从图3可以看出，在k=3处F(n，k)-k曲线最陡并出现拐弯，且β(k)-k曲线，k=3时取值最大；所以可确最优定分类数k=3。从表1则可得出分为{1，2，3，4，5，6，7}{8，9，10，11}和{12，13，14，15，16，17，18}三类，即5月1日到7月10日为前汛期，7月11日到8月20日为主汛期，8月21日到10月30日为后汛期。

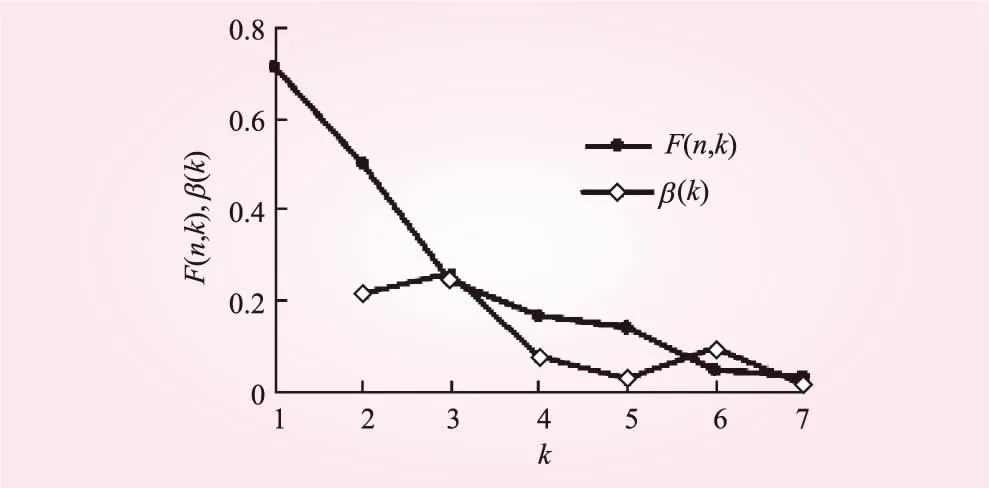
图3 F(n，k)-k和 β(k)-k曲线

2.3 洪水因素分析

2.3.1 样本指标选取及指标权重计算

在拟定的5月～10月为汛期的研究时段中，以旬为基本单位，将整个研究时段划分为18个旬。选取综合指标中3个洪水指标作为影响因子，运用SPSS软件对标准化的样本数据进行主成分分析，得各指标的权重

ω=(ω1，ω2，ω3)=(0.536，0.441，0.022)

2.3.2 分期计算

由于各指标间的单位不同，首先要将各指标进行无量纲化处理；再利用上面求得各指标的权重系数，对无量纲化的结果求加权平均值；最后计算得出初始分类样本向量Y=[0.22 0.30 0.31 0.55 0.26 0.27 0.36 0.77 0.73 0.52 0.53 0.46 0.43 0.47 0.20 0.57 0.28 0.04]T；再计算各截断样本的目标函数F(n，k)值。绘制目标函数F(n，k)-k和非负斜率β(k)-k曲线(见图4)。从图4可以看出，在k=3处F(n，k)-k曲线最陡并出现拐弯，且β(k)-k曲线，k=3时取值最大；所以可确最优定分类数k=3。从表1可以得出分为{1，2，3，4，5，6，7，8}{9，10，11，12，13}和{14，15，16，17，18}三类，即5月1日到7月20日为前汛期，7月21日到9月10日为主汛期，9月11日到10月30日为后汛期。

图4 F(n，k)-k和 β(k)-k曲线4结果与分析

季风环流是申村水库所属流域的主要气候影响因素。该流域以降雨补给为主，洪水特征取决于暴雨特征。该流域接近12月～2月份鼎盛的蒙古高压中心，降雨较少。6月～9月受东南季风支配，发育的小低压在山西与河南之间接触副热带海洋气团，形成了大量的降雨。又因地形抬升、对流以及气流向低压区幅合造成的气流抬升，都增大了该时段的降雨量，且大暴雨多发生在7月中旬到8月中旬。9月开始，气温开始降低，地面气压场开始转变，该流域开始受槽后西北气流控制，降雨开始减少。本文FAC-Fisher最优分割法以旬与侯为论域的划分结果，与降雨天气系统一致，符合洪水季节规律和成因特点。虽然北方地区公认的入汛期为6月～9月，但申村水库的降雨数据显示，5月降水总量为1998年、2004年与2009年的最大值，其余年内有时5月比6月的降雨量要多；10月降水量于1987年、1992年、1993年、1994年、1999年超过9月的降水量，其余年内有时10月降水量与9月相当。因此，把这两个月划分到汛期里也是有一定道理的。尤其是考虑到气候变化和极端天气这两个因素。

对于申村水库流域，依据综合指标得到5月1日到7月10日为前汛期，7月11日到8月30日为主汛期，8月31日到10月30日为后汛期；依据暴雨指标得到库5月1日到7月10日为前汛期，7月11日到8月20日为主汛期，8月21日到10月30日为后汛期；依据洪水指标得到5月1日到7月20日为前汛期，7月21日到9月10日为主汛期，9月11日到10月30日为后汛期。可以看出，基于洪水指标的分期滞后于基于暴雨指标的分期；而基于综合指标的分期基本介于两者之间，体现了洪水是暴雨与地表下垫面等多种因素综合作用的反映；洪水要滞后于暴雨，这与实际情况是相符的，一定程度上反映了汛期分期的物理背景。

3 结论与建议

(1)采用PCA-Fisher最优分割法对申村水库进行汛期分期，得到的分期结果能够较好地反应申村水库流域的暴雨洪水特征，可见PCA-Fisher最优分割法在汛期分期中具有较好的适用性。

(2)利用Fisher进行汛期分期所需指标的权重，本文利用PCA能够定量计算，进一步保证了分割结果的合理性和可靠度。

(3)汛期分期结果与分期指标有密切关系，实际应用时应综合考虑多种指标，让分期结果更客观。另外，也可以利用不同指标的分期结果，提供防洪安全或挖掘洪水资源的潜力。

(4)本研究表明，5月和10月归入申村水库汛期合理，人为判定汛期定为6月～9月缺乏对气候变化和极端天气等因素的考虑，在今后的研究中需对气候变化等因素对汛期的影响做深入研究。

参考文献：

[1] PENG Yang, JI Changming, LIU Fang. Impounding time and objective decision of Siluodu-Xiangjiaba cascade reservoirs in the flood recession period[J]. Journal of Basic Science and Engineering, 2014, 22(6)： 1098- 1107．

[2] 莫崇勋, 钟欢欢, 王大洋, 等. 集对分析方法在澄碧河水库汛期分期中的应用[J]. 水力发电, 2016, 42(1)： 14- 17．

[3] 喻婷, 郭生练, 刘攀, 等. 水库汛期分期方法研究及其应用[J]. 中国农村水利水电, 2006(8)： 24- 26, 56.

[4] 刘克琳, 王银堂, 胡四一. Fisher最优分割法在汛期分期中的应用[J]. 水利水电科技进展, 2007, 27(3)： 14- 16, 37．

[5] 莫崇勋, 王大洋, 朱新荣, 等. Fisher最优分割法在澄碧河水库汛期分期中的应用[J]. 水力发电, 2017, 43(6)： 19- 22, 27．

[6] 李俊, 武鹏林. 改进的Fisher最优分割法在汛期分期中的应用[J]. 中国农村水利水电, 2016(11)： 23- 26, 30．

[7] 张琳, 李长俊, 苏欣, 等. 模糊层次分析法确定管线风险因素权重[J]. 石油机械, 2006, 34(6)： 43- 45.

[8] WANG Hejia, XIAO Weihua, WANG Jianhua, et al. The impact of climate change on the duration and division of flood season in the Fenhe River Basin[J]. Water, 2016(8)： 1- 11．