基于图像配准的非均匀性校正算法

李成立,吕俊伟,刘 亮,王佩飞

(海军航空大学,山东 烟台 264001)

1 引 言

红外成像系统因为信噪比高、探测能力强以及结构简单等因素,被广泛应用到红外制导导弹和红外光电载荷上。但由于焦平面阵列各个探测单元的响应存在非均匀性,所以在相同辐射条件下会产生固定图案噪声,严重影响红外成像的质量[1]。而且,当温度或者其他环境条件改变时,剩余非均匀性会随着时间发生缓慢的漂移[2]。所以在红外制导导弹和红外光电载荷使用之前要先对其成像系统进行非均匀性校正(nonuniformity correction,NUC)。

基于场景的非均匀性校正可以解决时间漂移的问题[3],但当场景保持静止或者帧间位移不足时,会把场景当作非均匀性噪声进行校正,当场景再次运动时,图像上就会产生“鬼影”。文献[4]中指出对图像边缘像素估计不准确是“鬼影”产生的原因,并根据该分析提出基于边缘信息指导的自适应非均匀性校正算法(edge directed neural network nonuniformity correction,ED-NN-NUC),但该方法依赖对边缘提取的准确性。文献[5]中提出的空域低通时域高通算法(space low-pass and temporal high-pass filter,SLTH),只对图像高频部分进行处理,降低了低频部分场景信息对校正系数的影响,有效地抑制了“鬼影”。但是算法对边缘和非均匀性噪声的区分依赖于阈值的大小。文献[6]中提出基于双边滤波器的时域高通滤波算法(bilateral filter-based temporal high-pass filter,BFTH),对“鬼影”的抑制效果较为明显,但当场景中出现运动速度较慢的高亮度区域时,校正系数会出现错误的更新,使得“鬼影”现象依然存在,降低了算法的校正精度。

基于相邻两帧红外图像之间差别较小,结合帧间配准技术,本文提出了一种基于图像配准的非均匀性校正算法。与高通滤波类算法相比,本文算法得到的残差图像更好地消除图像中的场景信息,取得更好的非均匀性校正效果,对“鬼影”现象产生很好的抑制作用。

2 高通滤波类算法及其存在问题

在时间域上,非均匀性噪声属于低频成分,而场景属于高频成分。时域高通滤波算法(temporal high pass filtering,THPF)通过滤除图像中的低频成分,从而实现非均匀校正,整个过程可以看做一个时域上的高通滤波,即:

Yn=Xn-fn

(1)

(2)

式中,Xn表示第n帧非均匀图像;Yn为校正输出,fn为校正系数;是第n帧的低通输出;M是预先设定的时间常数。THPF算法容易实现,其不足之处在于场景存在连续多帧静止或者高亮度区域时会影响校正效果,产生“鬼影”现象。

ZUO在文献[6]中采用双边滤波器进行图像预处理。双边滤波器在处理图像时具有更好的去噪保边效果。其算法可表述为：

Yn=Xn-fn

(3)

(4)

(5)

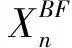
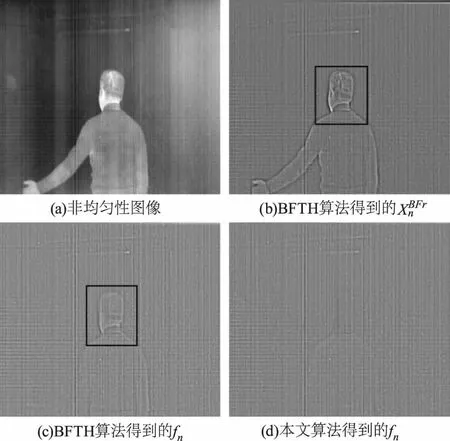
图1 图像分离结果Fig.1 Image separation result

3 基于图像配准的非均匀性校正算法

3.1 本文算法描述

在计算校正系数fn的过程中,剩余边缘及高亮度部分会通过与已有的校正系数fn-1进行加权平均而得到衰减,但是并不能做到完全消除。图1(c)为BFTH算法得到的校正系数fn,身体边缘和高亮区域得到了很大的抑制,但是仍有残余,这些残留的信息会在校正后的图像上形成“鬼影”。可以看出,高通滤波类算法产生“鬼影”现象是由于大量不相关的场景信息的存在所导致的,为了克服高通滤波类算法存在的缺陷,本文提出一种基于图像配准的非均匀性校正算法,算法流程如图2所示。

图2 本文算法流程图Fig.2 Block diagram of the proposed algorithm

算法步骤如下：

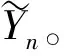
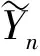
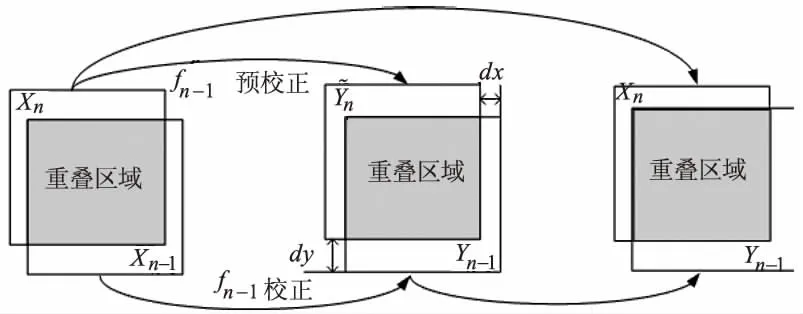
图3 前后两帧重叠区域示意图Fig.3 Overlapped area of two frames

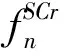
(4)利用式(7)对fn进行迭代更新。

(5)利用式(6)校正当前帧Xn,得到Yn。

算法可表述为：

Yn=Xn-fn

(6)

(7)

(8)

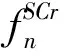
3.2 初值的选择

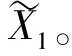
(9)

用均方根误差RMSE对各种滤波算法的效果进行衡量,X1经三种滤波器滤波后的RMSE如表1所示。

表1 首帧图像滤波后的RMSETab.1 RMSE of first filtered frame

从表1中可以看出,当采用三边滤波器时得到的残差图像的RMSE最低,校正效果最理想。所以算法在实现时,初值f1设置为三边滤波器得到的残差图像。

3.3 M的选择

在式(7)中,1/M表示的是校正系数fn的更新速率。随着M取值的增大,fn受当前帧的影响减小,更新速率变慢。将M设置为20、50、100、200四种情况,并计算校正结果的RMSE,以便考察其对算法收敛速率和校正能力的影响。将得到的RMSE曲线显示在图4中。

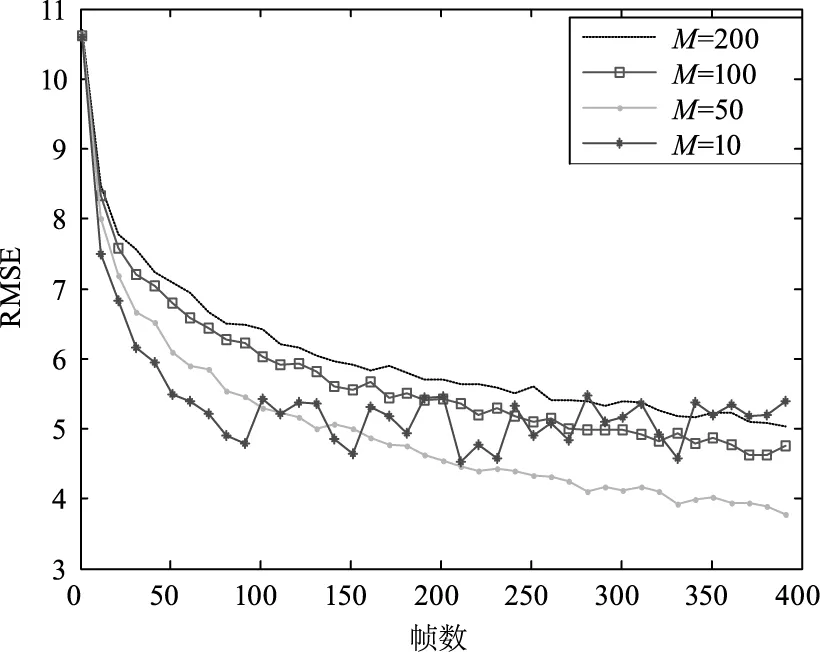
图4 不同M值时校正结果的RMSEFig.4 RMSE of the correction results with different M

从图中可以看出,当M取值为10时,虽然曲线收敛的最快,但是收敛后一直处于振荡状态中,校正效果不稳定。随着M取值的增大,曲线收敛速度逐渐变慢,但是曲线收敛后,校正效果趋于稳定。在50、100、200三个值中,当M取值为50时,校正结果的RMSE最小,算法收敛速度也最快。所以在算法实现时,可将M设置为50。更多的实验证明,M取值只要在30～60范围内,算法都可以取得较快的收敛速度和较稳定的校正效果。

4 校正实验及其结果分析

为了验证本文算法的校正效果,利用一段真实拍摄的带有非均匀性的红外视频进行测试。视频使用1161型长波非制冷热像仪在关掉非均匀性校正的情况下拍摄,帧频为30 f/s。序列1内容为近距离拍摄的人在室内行走的视频,共有450帧。序列2内容为在公路上的行驶汽车的视频序列,共有350帧,分别用SLTH算法、BFTH算法和本文算法对视频序列进行非均匀性校正。校正时,将M设置为50。

4.1 序列1的实验验证

为了直观地显示算法的校正结果,以视频序列中的第238帧图像为例,将其校正系数及校正结果进行显示。在第238帧中出现的人体目标运动速度较小,导致其脸部区域在连续多帧中表现为高亮度区域。这些区域在更新校正系数时贡献较大,所以在SLTH算法和BFTH算法生成的校正系数中包含一部分高亮度信息。另外由于身体边缘部分在空域上表现为高频,所以无论是SLTH算法还是BFTH算法,都不可能将边缘对校正系数的影响完全消除。如图5(a)(c)所示,在人的脸部有一片区域灰度值明显偏高,而且残留了身体的边缘信息,最终在对应的校正图像上人的头部和身体边缘右方出现了亮度较低的鬼影,如图5(b)(d)所示。本文对场景信息进行配准删除,消除了场景信息对非均匀性校正的影响,本文得到的校正系数和校正结果如图5(e)(f)所示,其校正结果中“鬼影”现象得到很好地抑制。

图5 不同校正算法得到的校正系数及结果Fig.5 fn and results obtained with different algorithms

在处理真实的非均匀性图像时,一般来说不可能获得理想的图像来对校正算法进行对比验证,也不可能得到均方根误差RMSE。此时,可用粗糙度[10]ρ来对非均匀性进行衡量。粗糙度计算公式为：

(10)

式中,h1、h2为水平和垂直方向的差分滤波器;I为待分析图像;‖f‖1表示f的l1范数;*表示离散卷积。ρ的值越小,表示非均匀性程度越弱。ρ的值越大,表示非均匀性程度越强。

图6 序列1校正后图像的粗糙度曲线Fig.6 Roughness of sequences 1 corrected by three algorithms

统计序列1经三种算法校正之后结果图像的粗糙度,做出曲线如图6所示。经本文算法校正后的图像的粗糙度曲线最低,即本文算法在此场景下校正效果良好,可以有效的去除场景中的非均匀性。

表2显示了三种算法得到的450帧校正后图像所有的平均粗糙度、总处理时间及处理速度。根据表2可知,本文算法校正结果的平均粗糙度是SLTH的78%,处理速度是BFTH算法的1.63倍。所以从校正效果和处理速度两方面综合考虑,本文算法要优于SLTH和BFTH两种算法。

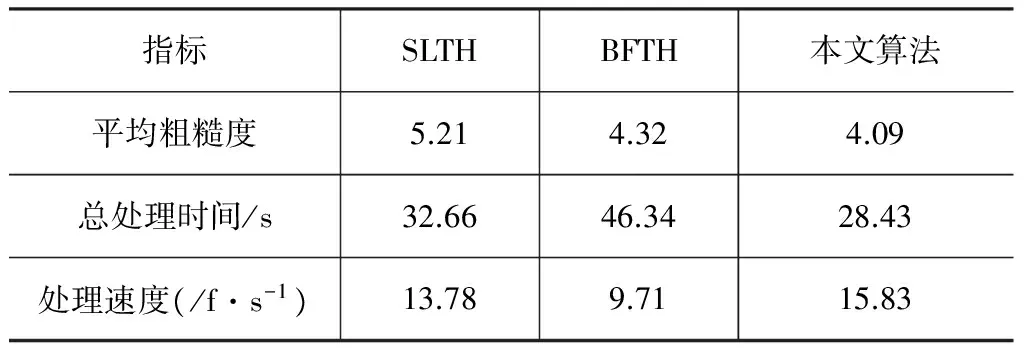
表2 三种算法校正能力比较Tab.2 Comparison of the correction ability of three algorithms

4.2 序列2的实验验证

以视频序列2中的第100帧非均匀性图像为例,如图7(a)所示,分别利用SLTH、BFTH和本文算法对其进行非均匀性校正,校正结果图像如图7(b)(c)(d)所示。可以看出,本文算法在此种场景下校正效果良好,非均匀性噪声得到了很好的校正。

图7 不同校正算法得到的校正结果Fig.7 Results obtained with different algorithms

统计序列2经三种算法校正之后结果图像的粗糙度,做出曲线如图8所示。经本文算法校正后的图像的粗糙度曲线最低,即本文算法在此场景下校正效果良好,可以有效去除场景中的非均匀性。

图8 序列2校正后图像的粗糙度曲线Fig.8 Roughness of sequences 2 corrected by three algorithms

5 结 论

本文针对高通滤波类算法的缺陷,结合帧间配准技术,提出了一种基于图像配准的非均匀性校正新算法。与在SLTH算法和BFTH算法中利用经过滤波器滤波后得到的残差图像迭代更新校正系数相比,本文算法得到的残差图像能更好地消除了图像中的场景信息,有效的抑制了“鬼影”现象,取得更好的校正效果。

参考文献：

[1] SHI Haoran,LI Zhaolong,SHEN Tongsheng.Research on nonuniformity correction of inf-rared focal plane array[J].Laser & Infrared,2016,46(2):204-208.(in Chinese)

史浩然,李召龙,沈同圣.红外焦平面阵列非均匀性的校正方法研究[J].激光与红外,2016,46(2):204-208.

[2] REN Jianle,CHEN Qian,QIAN Weixian,et al.Multiframe registration based adaptive non-uniformity correction algorithm for infrared focal plane arrays[J].J.Infrared Millim.Waves,2014,33(2):122-128.

[3] LI Zhaolong,HAN Yulong.Blind pixel detection and correction of IR imaging based on scene[J].Laser & Infrared,2017,47(4):465-469.(in Chinese)

李召龙,韩玉龙.基于场景的红外成像系统盲元检测及校正[J].激光与红外,2017,47(4):465-469.

[4] Zhang Tianxu,Shi Yan.Edge-directed adaptive nonuniformity correction for staring infrared focal plane arrays[J].Optical Engineering,2006,45(1):016402.

[5] Qian Weixian,Chen Qian,Gu Guohua.Space low-pass and temporal high-pass nonunifor-mity correction algorithm[J].Optical Review,2010,17(1):24-29.

[6] Zuo Chao,Chen Qian,Gu Guohua,et al.New temporal high-pass filter nonuniformity corre-ction based on bilateral filter [J].Optical Re-view,2011,18(2):197-202.

[7] LIU N,QIU H.A time-domain projection-based registration-scene-based nonuniformity correction technology and its detailed hardw-are realization[J].Optical Review,2014,21(1):17-26.

[8] YU Shikong,Xiang Wei,Zhao Yaohong,et al.An adaptive nonuniformity correction algorithm for infrared focal plane array[J].Journal of Computer-Aided Design & Computer Graphics,2016,28(1):138-145.(in Chinese)

于世孔,向伟,赵耀宏,等.一种自适应非均匀性校正算法[J].计算机辅助设计与图形学学报,2016,28(1):138-145.

[9] LI Jia,QIN Hanlin,YAN Xiang,et al.Temporal- spatial nonlinear filter based non-uniformity correction method for IR image sequence[J].Acta Photonica Sinica,2015,44(4):0410001-0410001-5.(in Chinese)

李佳,秦翰林,延翔,等.时空域非线性滤波红外序列图像非均匀性校正[J].光子学报,2015,44(4):0410001-1-0410001-5.

[10] LI Zhaolong,SHEN Tongsheng,LOU Shu li.Scene-based nonuniformity correction based on bilateral filter with reduced ghosting[J].Infrared Physics & Technology,2016,77:360-365.