红外图像超分辨率重建技术研究

王 岳,李双喜,王 磊

(安徽科技学院电气与电子工程学院,安徽 蚌埠 233100)

1 引 言

红外成像技术在现代军事上被广泛使用,其中主动红外成像具有对目标与周围环境间温差不敏感的优点,可弥补被动红外成像的不足,在现代战争中起着至关重要的作用。但红外图像受探测单元尺寸、探测器阵列采样密度等固有因素的限制[1],存在分辨率与信噪比较低的特点,有时无法满足实际应用需求。

提升红外图像分辨率最直接的方法便是升级红外成像设备。由于我国在红外成像技术起步较晚,许多关键技术没有完全突破,总体水平较西方发达国家有较大差距,且西方国家对我国购买红外设备设置了严格的限制,使得在较短时间内通过硬件升级来提升红外图像分辨率的方法难以实现。所以对已有红外图像的分辨率提升技术研究能够在一定程度上弥补已有设备的不足。超分辨率重建技术可以在不改变成像系统的情况下,对具有互补信息的低分辨率图像序列进行处理,重建出一幅或多幅高分辨率图像的技术[2]。该技术的重建能力是指在低分辨率图像序列含有噪声时,通过这些图像序列可以恢复出的原始高分辨率图像的信息数量[2-3]。

在主动红外成像中,除了常见的散斑噪声这种乘性噪声外,往往还会混入热噪声等加性噪声。噪声的存在不仅会引起图像边缘纹理等细节信息的劣化,在超分辨重建过程中还会扩散至重建图像中,造成重建图像信噪比降低。本文对低分辨率红外图像序列中存在的噪声进行了研究,提出首先对含噪图像序列使用基于NSCT变换的自适应噪声抑制方法进行预处理,之后采用自适应正则化进行超分辨重建的两步方法,实验结果证明了本文算法的有效性。

2 含噪红外图像序列的超分辨率重建分析

2.1 超分辨重建模型

噪声对超分辨率重建的影响,可以通过图像的超分辨率重建过程进行分析。典型的图像降质及其超分辨率重建模型如图1所示。设低分辨率图像序列{yk,k∈[1,N]}包含N帧图像,其图像尺寸均为M×N,x是大小为Mp×Nq的高分辨率图像。x→y的降质过程可以表示为：

yk=DBkMkx+nkk∈[1,N]

(1)

式中,D为降采样矩阵;Bk表示由点扩散函数或衍射极限引起的模糊矩阵;Mk表示由于运动引起而引起的变形矩阵;nk表示零均值的高斯白噪声。由图可以看出,图像的超分辨率重建过程是在实际得到低分辨率图像序列{yk,k∈[1,N]}信息基础上,重建出高分辨率图像x的过程。

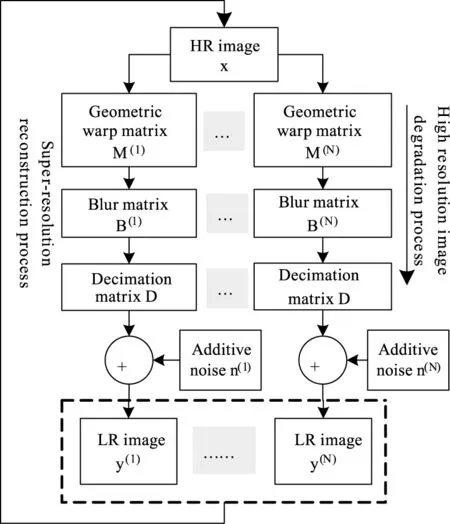
图1 图像降质及其超分辨率重建模型Fig.1 Image degradation and superresolution reconstruction model

2.2 红外图像的噪声对超分辨重建的影响

红外成像系统在使用中,得到的图像除了散斑噪声这种主要噪声外,往往还夹杂着热噪声等加性噪声。因此含噪的红外图像可以表示为：

z(i,j)=m(i,j)x(i,j)+n(i,j)

(2)

式中,z(i,j)表示实际得到的红外图像;m(i,j)表示散斑噪声;x(i,j)为原始红外图像;n(i,j)表示混入的加性噪声。

由式(1)可知,超分辨率重建的过程就是图像降质的逆过程。通过公式可以直观地表示为：

(3)

将式(2)与式(1)代入式(3)中,可得:

(4)

式中,m表示乘性噪声;n表示加性噪声。根据解析延拓理论,重建过程是在原有图像低频信息进行复原的基础上,实现对截止频率之外信息的重建。重建后的图像相对原序列图像,其分辨率实现了提高,相当于增加了图像的细节信息,但同时也会带来噪声的扩散。其中散斑噪声对于重建图像的影响还会随红外图像像素灰度的变化而变化,严重影响到图像的军事应用及后续处理。因此对红外图像进行预处理是十分必要的。

3 基于NSCT变换的图像去噪

传统的散斑噪声抑制方法如同态维纳滤波、Lee滤波、自适应滤波等方法,在抑制噪声的同时也会造成图像细节信息的模糊[4-5]；小波变换由于其良好的时频特性,近年在图像处理领域得到了广泛的应用[6-8]。但小波变换缺乏多方向性与平移不变性[9-10]：方向性的缺乏则不能有效反映图像多方向的基本组成信息,造成细节信息的损失；不具备平移不变性则会使得去噪后的图像出现寄生波纹,如边缘振铃与吉布斯效应。

NSCT变换(Non-subsample Contourlet Transform)[11]是Cunha等人在2005年提出的一种非正交变换,由非下采样的塔式变换与非下采样的方向变换两部分组成。前者用于对图像进行多尺度分解,后者实现对图像的多方向分解。这种分解方式可有效避免子带间的混叠,有效表示图像的细节信息。由于去掉了Contourlet变换中的下采样环节,使得NSCT变换具备了平移不变性可以在进行散斑噪声抑制的同时对图像边缘与细节部分进行较好的保持,更有利于图像处理后的效果。因此本文采用NSCT变换对含噪图像进行分解,其过程的如图2所示。

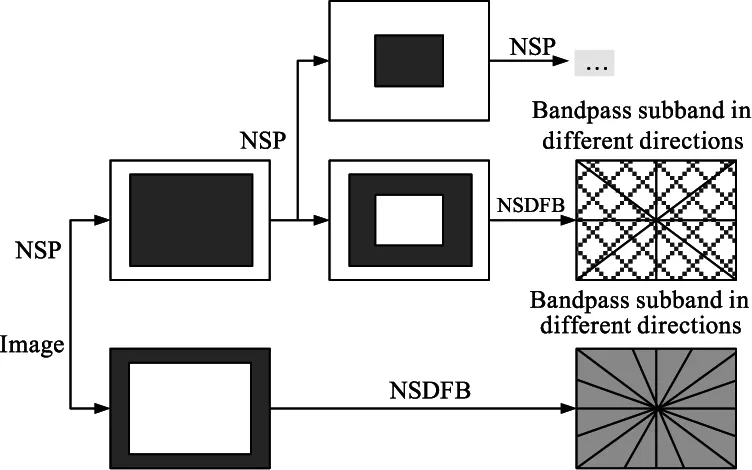
图2 NSCT的分解过程Fig.2 Decomposition of NSCT

4 红外图像序列中噪声的预处理

在2.2节中已证明红外图像中两种噪声在超分辨过程中都会扩散进而造成重建图像质量的降低,为了抑制噪声,本文使用两次的NSCT变换以分别对图像中加性噪声与乘性噪声进行处理。为防止预处理造成图像信息的过多损失,分解尺度均设定为2。

4.1 对加性噪声的处理

在含噪红外图像中,加性噪声相对散斑噪声对红外图像影响较小,本文采用软阈值法对其进行处理。设此时含噪图像可表示为z(i,j)=g(i,j)+n(i,j),其中g(i,j)=m(i,j)x(i,j)。在NSCT变换后,系数满足z(k)=g(k)+n(k),此时软阈值函数可表示为：

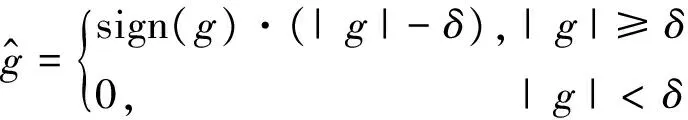
(5)

为准确估计NSCT变换后噪声方差,首先对红外图像进行正交小波变换,设变换后小波系数满足z′(k)=g′(k)+n′(k),此时用Donoho鲁棒性方法对图像中噪声方差σ2进行估计：

(6)

4.2 对乘性噪声的处理

4.2.1 基于P-Laplace模型的低频处理

多尺度变换后的低频部分若不进行一定处理,所包含的噪声容易使去噪后的图像在平滑区域产生阶梯效应(stair effects),影响图像的后续处理与应用。改进的P-Laplace模型[13]可以通过图像中噪声的分布情况进行自适应调整,能够在去除噪声的同时更好地保护图像结构信息,因此本文选用此模型对低频部分进行处理,其模型可以表示为：

(7)

其中，J(z)代表能量函数;p∈[1,2]；▽代表梯度算子；λ为朗格朗日常数；p为扩散因子。计算可知：在图像平坦区域,能较好地去除噪声；在图像的非平坦区域,能较好地对图像结构信息进行保护[14]。

4.2.2 基于统计模型的高频处理

含噪红外图像经对数处理与NSCT变换后,其高频部分的噪声系数根据统计特性可以建模为瑞利分布[15],其概率密度函数(Probability density function,PDF)为：

(8)

式中,α表示衰减参数;θ(·)为阶跃函数。

原始红外图像x(i,j)在变换后,其系数可以建模为拉普拉斯分布[16]：

(9)

其中,σx表示拉普拉斯模型的边缘标准差。

对实际红外图像z(i,j),根据最大后验估计理论,可得：

(10)

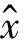
(11)

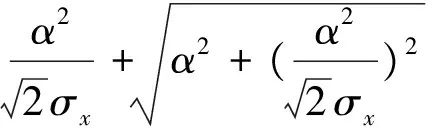
4.2.3 衰减函数与边缘标准差的计算

对于乘性噪声m(i,j),在进行NSCT变换后其系数分布是正负对称的,所以其均值,即Em=0；其均值与方差之间满足Dm=Em2-(Em)2。Em2结合式(8)可以表示为：

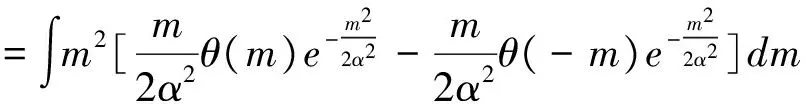
=2α2

(12)

对Dm=Em2-(Em)2化简后可得如下关系：

(13)

对边缘标准差σx,可以使用局部自适应法进行估计,即以当前NSCT系数为中心的窗口内的系数对当前NSCT系数的边缘标准差进行估计：

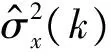
(14)

(15)

5 自适应正则化的超分辨重建

5.1 正则化超分辨重建

通过对红外图像噪声的预处理,可减少噪声在超分辨重建过程中因扩散对图像质量的影响。对预处理后的红外图像进行超分辨重建,除噪声外,还涉及配准、去模糊等多种图像处理问题,从数学的角度看,该过程是Hardmard意义下的不适定问题(ill-posedness),需要采用正则化方法进行处理。

此时图像的降质模型可以表示为：

xk=DBkMku+vkk∈[1,N]

(16)

其中,{xk,k∈[1,N]}为经过预处理的红外图像序列;u表示待重建的高分辨率图像;vk表示预处理后图像中残留的噪声。红外图像超分辨重建过程的正则化框架可表示为：

(17)

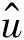
传统的正则化方程中,φ(u)=‖Cu‖2,C为稳定因子,通常为高通算子,其作用是对不适定问题的解中的高频成分做平滑性约束,用以约束解的稳定性。但图像的细节信息也为高频部分,因此采用高通算子的传统正则化方法会造成重建后图像细节信息的模糊,而且传统正则化方法也没有充分考虑图像配准误差对重建图像质量的影响。

5.2 自适应正则化的超分辨重建

为减少传统正则化方法造成的图像细节信息模糊与配准误差产生的影响。本文提出在Lee正则化方程[17]的基础上,结合Huber马尔科夫先验模型[18]以减少配准误差的影响,同时实现对重建图像细节信息的自适应保护,其形式如下：

(18)

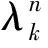
(19)

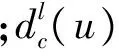
(20)

(21)

由公式可知,Huber先验模型通过分段函数ρ(i)实现对图像不同区域先验约束的控制,通过衡量图像的区域特征,实现对图像细节信息的自适应保护；正则化参数λn也可以根据式(19)进行自适应调整,要优于传统正则化方程中的全局性参数。

对式(18)可以采用最速梯度下降法进行迭代求解,即从红外图像序列中迭代更新待求的高分辨率红外图像直至求得的结果满足设定的收敛条件。具体可以表示为：

(22)

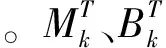
5.3 红外序列图像超分辨重建算法描述：

1)将原始含噪红外图像用NSCT变换进行2层分解,对分解得到的方向系数进行软阈值处理,以消除红外图像中所含的加性噪声n(i,j)。

2)对此时的含噪红外图像进行对数变换,将乘性噪声转化为加性噪声进行处理。因为z(i,j)∈[0,255],为防止z(i,j)=0情况的出现,设：

z(i,j)=[m(i,j)+η][x(i,j)+μ]

(23)

η与μ皆为非零常数。上式经对数变换可得：

Inz(i,j)=Inm′(i,j)+Inx′(i,j)

(24)

3)对Inz(i,j)用NSCT变换进行2层分解,每层方向数为(4,4)。设NSCT系数满足z(k)=m(k)+x(k),对变换后得到的低频部分使用4.2.1节中改进的P-Laplace模型进行处理；变换得到的高频部分则使用4.2节中基于统计模型的方法进行处理。根据噪声分布的不同,对低频部分与高频部分分别进行处理以达到较好的去噪效果。

4)对处理后得到的系数做NSCT反变换,再进行指数变换,重复以上步骤,最终可得到抑制噪声后的红外图像序列{xk,k∈[1,N]}。

5)以图像序列中的x1作为参考图像,使用光流法对低分辨红外之间的亚像素位移进行配准求解,并计算式(18)中数据保真项与正则项的梯度函数。

6)通过式(19)计算正则化参数λk；使用DDT插值法[19]将x1插值为尺寸与待重建图像u相同的图像u0,将u0作为初始估计图像,结合以上所求代入式(22)中迭代求解高分辨率红外图像。当求解结果符合设定的收敛条件时(本文设定为迭代收敛偏差),停止计算,此时便可得到重建的高分辨红外图像u。

6 实验结果与分析

为了验证上述算法的有效性,本文选用在去除散斑噪声中常用的Lee滤波结合本文超分辨重建方法与本文算法进行了对比。在第一组实验中,选定尺寸为256×256的“cameraman”作为原始参考图像,采用峰值信噪比(PSNR)、结构相似性指数(SSIM)与相关系数(CC)三个指标,综合对图像重建结果进行衡量。

在实验中,将“cameraman”图像在水平与垂直方向作0～2个像素的随机移动、图像的模糊过程采用方差为1的[5×5]的高斯模糊核,按文献[20]方法,产生均值为0,方差为0.02的乘性噪声与参考图像相乘得到模拟的加斑图像,进行2倍的下采样后添加方差为0.02的高斯白噪声后,生成9幅实验用低分辨率图像序列进行超分辨重建，如图3所示。

图3 cameraman图像去噪及其超分辨重建结果Fig.3 denoise and its super-resolution result of cameraman image

从图3(c),(d)可以看出,本文在图像预处理中去噪考虑了不同类型噪声,且在图像NSCT变换后,对高频部分与低频部分均进行了自适应去噪处理,相对传统的Lee滤波,在图像细节上视觉效果改善明显；在随后的超分辨重建中,基于本文预处理方法得到的低分辨率图像序列重建的结果图3(f)在视觉效果上也要优于基于传统Lee滤波后重建得到的图3(e)。表1给出了超分辨重建后的客观指标的对比,表明本文算法的客观指标均高于对比算法,验证了视觉上更优的结果。

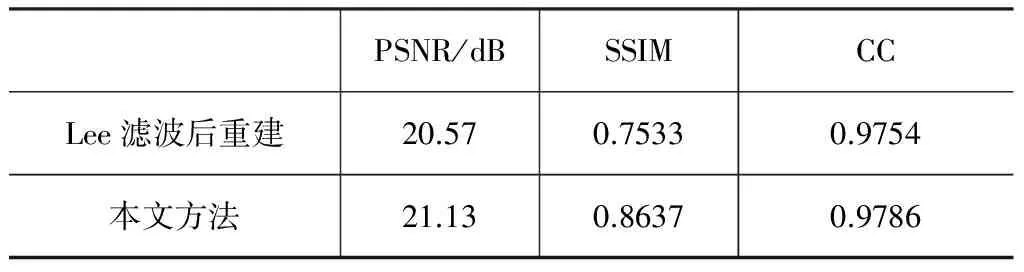
表1 cameraman图像超分辨重建的客观指标Tab.1 Reconstruction objective indicators of super-resolution image

为验证本文算法在实际应用中的有效性,在第二组实验中选用由某红外成像系统在夜间拍摄的尺寸为160×120的航行中船舶图像进行处理。超分辨重建因子设为2,以高斯模糊作为系统的PSF,选用光流法进行运动估计。因为没有原始参考图像,此处选用平均梯度值(G)作为重建图像的客观评价指标。

图4 实际红外图像序列的超分辨重建结果Fig.4 Super-resolution result of infrared image sequences 表2 红外序列图像超分辨重建后的梯度值 Tab.2 The gradient of reconstructed infrared image sequences

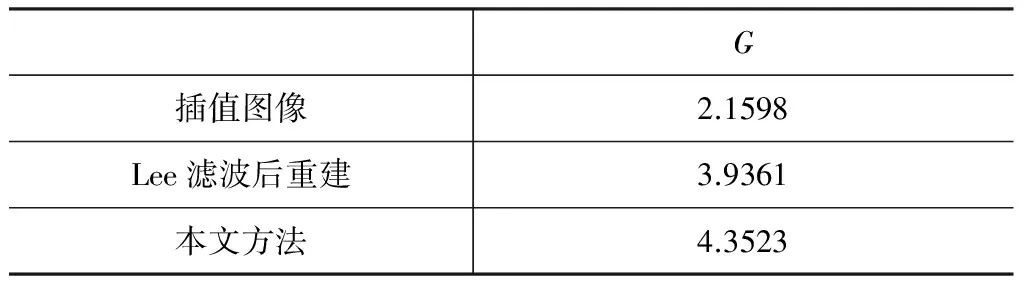
G插值图像2．1598Lee滤波后重建3．9361本文方法4．3523

从图4(d)、(e)、(f)可以看出,本文算法在抑制噪声提高分辨率的同时,能更好地保护图目标图像的边缘信息与轮廓结构,从表2可以看出本文算法所得到图像的平均梯度值比插值放大图像有大幅提升,与基于传统Lee滤波后的重建图像相比也有明显优势。

7 结 论

根据主动红外成像中噪声的特点,采用分两步的方法：首先用NSCT变换对红外图像序列进行预处理,与传统算法相比更为有效的抑制了图像噪声对后续超分辨重建的影响；在之后超分辨重建中采用了自适应的正则化方法,在减小重建误差的同时实现对重建图像细节的保护。实验结果表明本文算法提高了重建图像的质量。本文算法可弥补原有红外成像系统成像分辨率偏低的不足,对红外成像系统影像分辨率的增强是一种可行的方法。

参考文献：

[1] LIU Yanyan,ZHANG Xin,XU Zhengping,et al.Application of special-shaped-pixel detectors in super resolution reconstruction[J].Infrared and Laser Engineering；2009,38(6)：971-976.(in Chinese)

刘妍妍，张新，徐正平，等.赋形像元探测器在超分辨重建中的应用[J].红外与激光工程，2009，38(6)：971-976.

[2] ZHANG Liangpei,SHEN Huanfeng,ZHANG Hongyan,et al.Image super-resolution reconstruction[M].Beijing:Science Press,2012:19-20.(in Chinese)

张良培,沈焕峰,张洪艳,等.图像超分辨率重建[M].北京：科学出版社,2012 ：19-20.

[3] ZHANG Lei,YANG Jianfeng,XUE Bin,et al.Super-resolution reconstruction of Chang’e-1 satellite CCD stereo camera images[J].Infrared and Laser Engineering,2012,41(2)：404-408.(in Chinese)

张磊,杨建峰,薛彬,等.嫦娥一号卫星CCD立体相机影像超分辨率重建算法[J].红外与激光工程,2012,41(2)：404-408.

[4] J W Goddman.Some fundamental properties of s peckle[J].J.OPT.SOC,1976,66(11):1145-1150.

[5] Lee JS.Refined filtering of image noise using local statistics.Computer Graphic and Image Processing[J].1981,15(1):380-389.

[6] Loupas T,McDicken WN,Allen PL.An adaptive weighted median filter for speckle suppression in medical ultrasonic images[J].IEEE Transaction Circuits Systems,1989,36(1):129-135.

[7] WU Yiquan,YE Zhilong,WAN Hong.Speckle noise suppression of reconstructed image based on dual-tree complex wavelet and anisotropic diffusion[J].Chinese Journal of Laser,2013,40(4):0409002-0409008.(in Chinese)

吴一全,叶志龙,万红.双树复小波和各向异性扩散再现像散斑噪声抑制[J].中国激光,2013,40(4):0409002-0409008.

[8] LIU Bo,QU Youshan,FENG Gurlan,et al.Maximal PSNR wavelet bi-linear interpolation iterative algorithm in remote sensing image[J].ACTA Photonica Sinica,2006,35(3):468-472.

[9] CAI Nian,ZHANG Haiyuan,ZHANG Nan,et al.Using improved weighted parabolic interpolation and wavelet transformation to zoom images for super-resolution[J].Journal of Graphics,2012,33(1):50-55.(in Chinese)

蔡念,张海员,张楠,等.基于小波的改进加权抛物线插值的图像超分辨率算法[J].图学学报,2012,33(1):50-55.

[10] LI Hengjian,ZHANG Jiashu,CHEN Huaixin.Image denoising based on the sparse land using redundant bandelet transform[J].Journal of the China Railway Society,2010,32(5),108-112.(in Chinese)

李恒建,张家树,陈怀新.基于稀疏模型的Bandelet图像去噪方法[J].铁道学报,2012,33(1):50-55.

[11] Peyre G,Pennec E L,Dossal Charles.Geometric estimation with orthogonal bandlet based[C].Processing SPIE Wavelet XII.San Diego,2007.

[12] A L Cunha,ZHOU Jianping,Do M N.The nonsubsampled contourlet transform:theory,design and application[J].IEEE Trans on Image Processing,2006,15(10):3089-3101.

[13] Donoho D L.De-noising by soft-thresholding[J].IEEE Transaction Information Theory,1995,41(3):613-627.

[14] J J Chen.Image restoration based on adaptive P-Laplace diffusion [C].Yantai:Proceedings of IEEE International Congress on Image and Signal Processing,2010,1:143-146.

[15] Gupta S,Chauhan RC,Saxena SC.Locally adaptive wavelet domain Bayes processor for denoising medical ultrasound images using Speckle modeling based on Rayleigh distribution.[J].IEEE Proceedings Vision,Image and Signal Processing,2005,152(1):129-135.

[16] HOU Jianhua,XIONG Chengyi,HE Xiang,et al.Speckle reduction in medical ultrasound images based on wavelet and its statistical modeling[J].Chinese Journal of Biomedical Engineering,2009,28(1):31-36.

[17] Eun Sil Lee,Moon Gi Kang.Regularized adaptive high-resolution image reconstruction considering inaccurate subpixel regiatration[J].IEEE Transactions on Image Processing,2003,12(7):826-837.

[18] L P Zhang,H Y Zhang,H F Shen.A super-resolution algorithm for surveillance image[J].Signal Processing,2010,90(3):848-859.

[19] Dan Su,Philip Wills,Image interpolation by pixel-level data-dependent triangulation[J].Computer Graphics Forum,2004,23(2):189-201.

[20] Pizurica A,Philips W,Lemahieu I,et al.A versatile wavelet domain noise filtration technique for medical imaging [J].IEEE Transaction Medical Imaging,2003,22(3):323-331.