轨道交通混凝土桥梁中低频噪声预测方法

宋晓东， 李 奇， 吴定俊(. 东南大学 桥梁工程系， 江苏 南京 0096; . 同济大学 桥梁工程系， 上海 0009)

现场实测表明[1-2]，轨道交通混凝土桥梁的噪声主要在1 000 Hz以下，当采用A计权声压级时，桥梁结构噪声和轮轨噪声为主要的噪声源。Thompson[3]的研究表明，车轮辐射噪声主要在1 000 Hz甚至更高的频率以上才起主导作用，因此在1 000 Hz以下主要考虑桥梁结构噪声和钢轨噪声。关于轮轨噪声的研究已经相对较为成熟，Thompson[3]基于频域的振动耦合分析及简化的点、线声源辐射模型提出TWINS(Track-Wheel Interaction Noise Software)方法预测轮轨噪声，这一方法得到了广泛的运用。刘林芽等[4]利用类似的方法对铁路的轮轨噪声特性进行了研究。方锐等[5]利用3D有限元和声学边界元分析了轨道结构参数对轮轨噪声的影响。随着桥梁建设的快速发展，桥梁结构的辐射噪声问题引起了越来越多学者的关注。张迅[6]、李奇[7]、张楠[8]、杨新文[9]等结合车-轨-桥耦合振动和3D声学边界元对铁路桥梁和城市轨道交通桥梁的振动噪声进行了分析。吴天行[10]结合功率流和3D边界元方法对比了轨道交通U形梁和箱梁的噪声特性。由于3D边界元计算桥梁噪声较为费时，李奇、宋晓东[11-12]提出了基于空间波数变换的2.5D方法预测桥梁结构噪声，提高了计算效率且不失精度。上述研究主要针对200 Hz以下的低频桥梁噪声，用3D边界元方法预测桥梁中高频噪声极为费时。李小珍[13]利用统计能量法和简化的点、线声源模型对高速铁路钢桁结合梁的中高频结构噪声进行了研究。统计能量法适于模态密度较大的高频结构噪声问题，但是结构的损耗因子等相关参数较难准确获得。

桥梁噪声和钢轨噪声是轨道交通高架线路上的主要声源，上述研究很少同时对这两种噪声进行预测分析。在进行减振降噪研究时，有必要对两种声源的贡献进行分析，从而有针对性地选取降噪措施。本文将以一座混凝土U形梁为工程背景，结合3D车-轨-桥耦合动力分析和2.5D声学计算方法同时预测桥梁和钢轨的中低频噪声，并对两者的分布规律及噪声特性进行研究。

1 车辆-轨道-桥梁耦合振动

钢轨和桥梁的振动响应可通过文献[14]提出的基于模态叠加法的数值计算方法获得，车辆-轨道-桥梁动力学方程为

( 1 )

式中：q、ξ、ω、Φ分别为模态坐标矩阵、阻尼矩阵、圆频率矩阵、位移矩阵；f为荷载矩阵；下标v、t和n分别为车辆、轨道和第n跨桥梁；M为桥梁的总跨。

车辆、钢轨和桥梁3个子系统可以通过数值模型单独建立并进行模态分析，三者之间的连接不直接在数值模型中模拟，而是通过拟力法原理将子系统之间的连接力处理为虚拟激振力，并移到式( 1 )的右端，以实现3个子系统内部模态解耦[14]。虚拟激振力可通过迭代方法求解。

轮轨不平顺为车-轨-桥耦合振动的重要激励源，本文采用文献[15]中的不平顺限值谱，然后利用三角级数法生成空间不平顺样本，考虑接触滤波效应为[16]

( 2 )

式中：H(k)为接触滤波效应；k为波数；a为圆形接触斑的半径，通常取值为5～7.5 mm。

2 桥梁和钢轨噪声预测方法

在求得结构振动响应后，可以通过声模态传递向量方法计算结构辐射噪声[7]

( 3 )

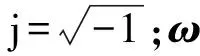
桥梁和钢轨的辐射总噪声可以通过叠加求得

MATVt(ω)TQt(ω)

( 4 )

由于MATV只跟结构自身有关，当车速、扣件刚度等参数变化时只需重新计算车-轨-桥耦合振动响应，而无需进行声学计算，因而便于参数分析。

3 空间波数变换计算MATV

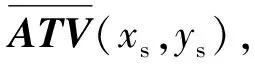
ATV(xs,ys,zs,k)=

( 5 )

式中：k为空间波数；kz为z方向的波数。

求得3D声传递向量后再将桥梁和钢轨的模态位移分别投影到结构表面外法向，根据式( 3 )获得桥梁和钢轨的MATV，最后结合车-轨-桥耦合振动结果求得各自的辐射噪声。

4 工程实例分析

4.1 工程概况及测试

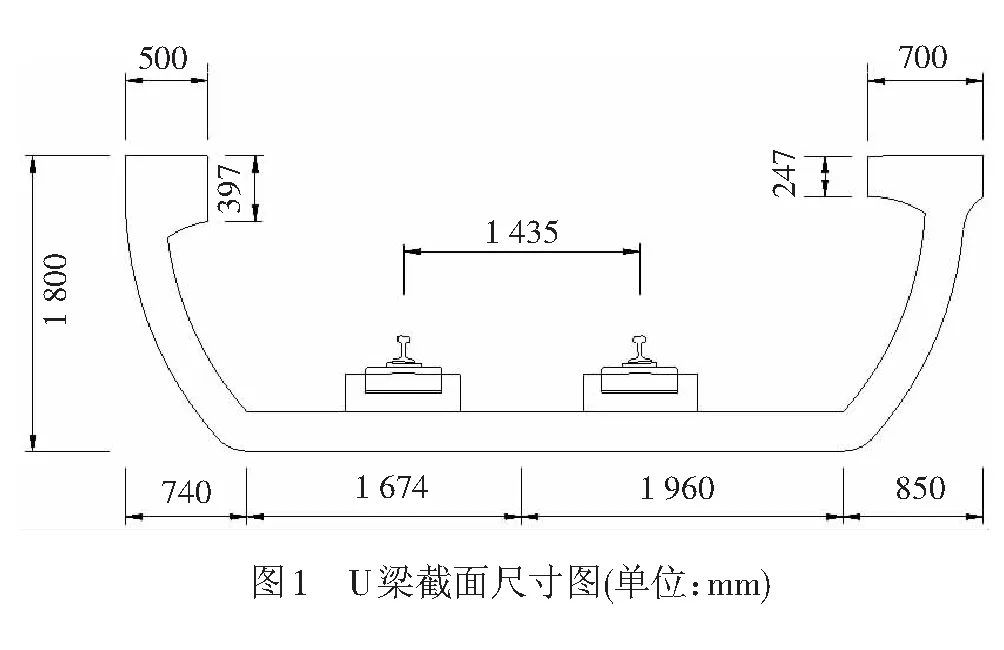
某25 m单线轨道交通U形梁的截面尺寸见图1。该桥梁顶底板和腹板的厚度均为240 mm，采用C55混凝土。钢轨与桥梁之间通过橡胶垫层和WJ-2型扣件连接。

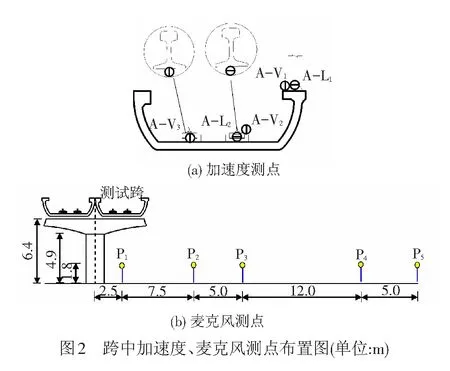
现场实测时，在跨中截面设置了5个加速度传感器，见图2(a)。其中，A-V1、A-V2、A-V3用于测试U梁顶板、底板承轨台和钢轨的竖向加速度，A-L1、A-L2用于测试顶板和钢轨的横向加速度。同时，在桥梁跨中断面U梁底板下方设置了5个麦克风测试噪声(P1～P5)，位置见图2(b)。测试现场的地面为沥青混凝土路面，可将地面当成刚性全反射面。测试时所用车辆为7节编组(1拖车+5动车+1拖车)，车辆速度为75 km/h。

4.2 数值计算模型

车辆采用多刚体模型，相关参数见文献[7]。U梁与钢轨均采用Ansys有限元软件中的8节点实体单元模拟，单元最大尺寸为0.1 m，局部放大有限元模型见图3。钢轨和桥梁的模态阻尼比分别取0.005、0.02。扣件竖向、横向刚度分别为60、20 MN/m，竖向、横向阻尼分别为60、80 kN·s/m。扣件不在Ansys中直接模拟，而在式(1)中作为虚拟力处理[14]。由文献[7]可知，U梁的桥墩仅对桥梁32 Hz以下的振动声辐射有影响，因此在研究U梁的中低频噪声时可以忽略桥墩的影响。轨道交通线路上往往采用等跨径和截面相同的多跨简支梁结构，在建模时可以只建立一跨有限元桥梁模型，而将其余跨简支梁视为与之相同的结构，从而大大降低有限元模型的自由度数量。列车过桥时的结构振动响应通过求解式(1)中的动力学耦合方程获得。

由于边界元方法在计算时存在频率不唯一等奇异性问题，因此采用声学软件中的有限元-无限元方法计算桥梁和钢轨的2D声传递向量。经过测试，声学有限元尺寸取0.03 m，无限元单元阶次取20阶，无限元边界半径取3 m可满足计算精度要求。然后通过编程计算实现波数变换获得3D的声模态传递向量。由于远场点的噪声受到相邻跨结构噪声的影响，因此要合理选择计算的桥梁模型跨数。经试算，采用3跨桥梁模型可以满足离轨道中心线30 m范围内的噪声预测精度要求。

4.3 实测与仿真对比

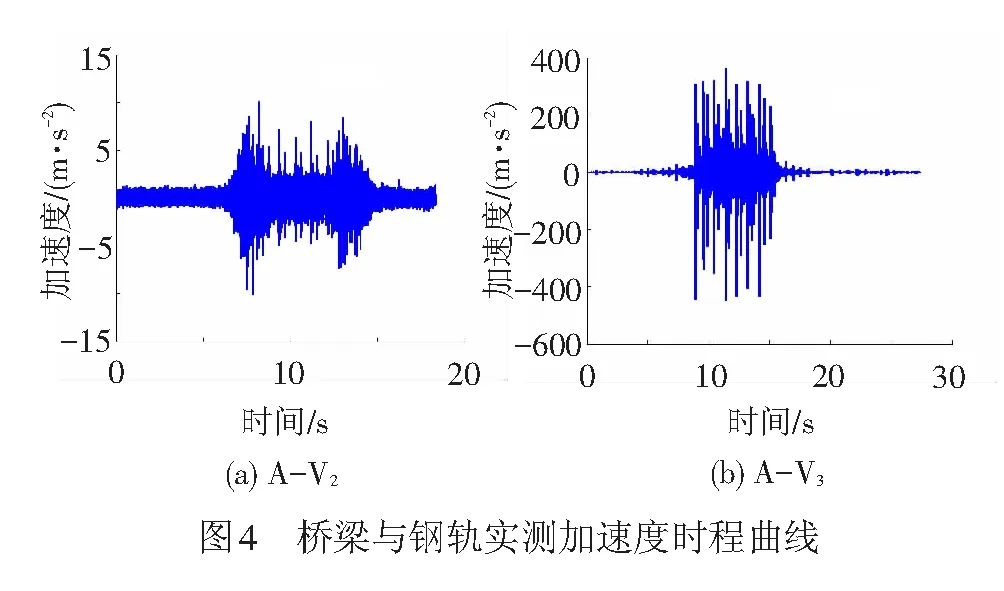
桥梁和钢轨的竖向加速度实测时程曲线见图4。由图4可见，列车通过时，钢轨的振动幅值远大于桥梁，当一系列轮对经过测点位置时，引起钢轨的振动峰值，最大峰值可达到400 m/s2左右。列车通过时间长度内的加速度频谱见图5(加速度参考值为10-6m/s2)，由图5可见，计算结果与实测结果趋势基本一致，除个别频段外两者基本吻合较好。由加速度测试结果可知，桥梁竖向振动在较宽的频带范围内都有较大的贡献，主要峰值频率位于40～80、256～512 Hz两个区间；而钢轨的竖向振动和横向振动幅值随着频率的提高不断增加，在200 Hz以上起较大的贡献。

P1、P2和P4测点的实测声压时程曲线见图6。由图6可知，对于离地面高度相同的测点，其离轨道中心线越近，声压幅值越大；随着场点远离桥梁，声压值逐渐衰减。然后，计算3跨U梁模型的辐射噪声，并与实测值进行对比，见图7。由图7可知，实测值与计算值总体趋势一致，对于近场点P1，两者相差很小；对于远场点，计算值在200 Hz以上小于实测值，且场点离轨道中心越远，相差越大。这是由以下原因造成的：(1)数值计算的结构振动结果与实测值存在一定的差异；(2)列车车身、车轮等边界条件会改变钢轨的声辐射指向性，本文的声学模型并未考虑这些因素的影响；(3)P1点位于桥梁正下方，主要为桥梁结构噪声，其他声源基本被U梁遮蔽，而对于远场点，车辆及设备噪声等其他声源对其也有一定的贡献，本文并没有考虑。

4.4 桥梁噪声与钢轨噪声特性

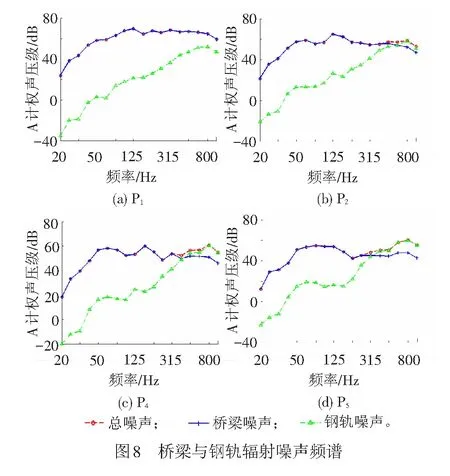
数值计算模型获得的不同场点位置的桥梁噪声和钢轨噪声频谱见图8。由图8可见，由于P1位于U梁正下方，钢轨噪声基本被U梁遮蔽，因此主要为桥梁辐射噪声；随着场点离轨道中心线的距离越来越远(P2～P5)，钢轨噪声对总噪声的贡献比重越来越大，对于离轨道中心线30 m的P5，钢轨噪声在300 Hz以上的贡献已经超过了桥梁噪声。

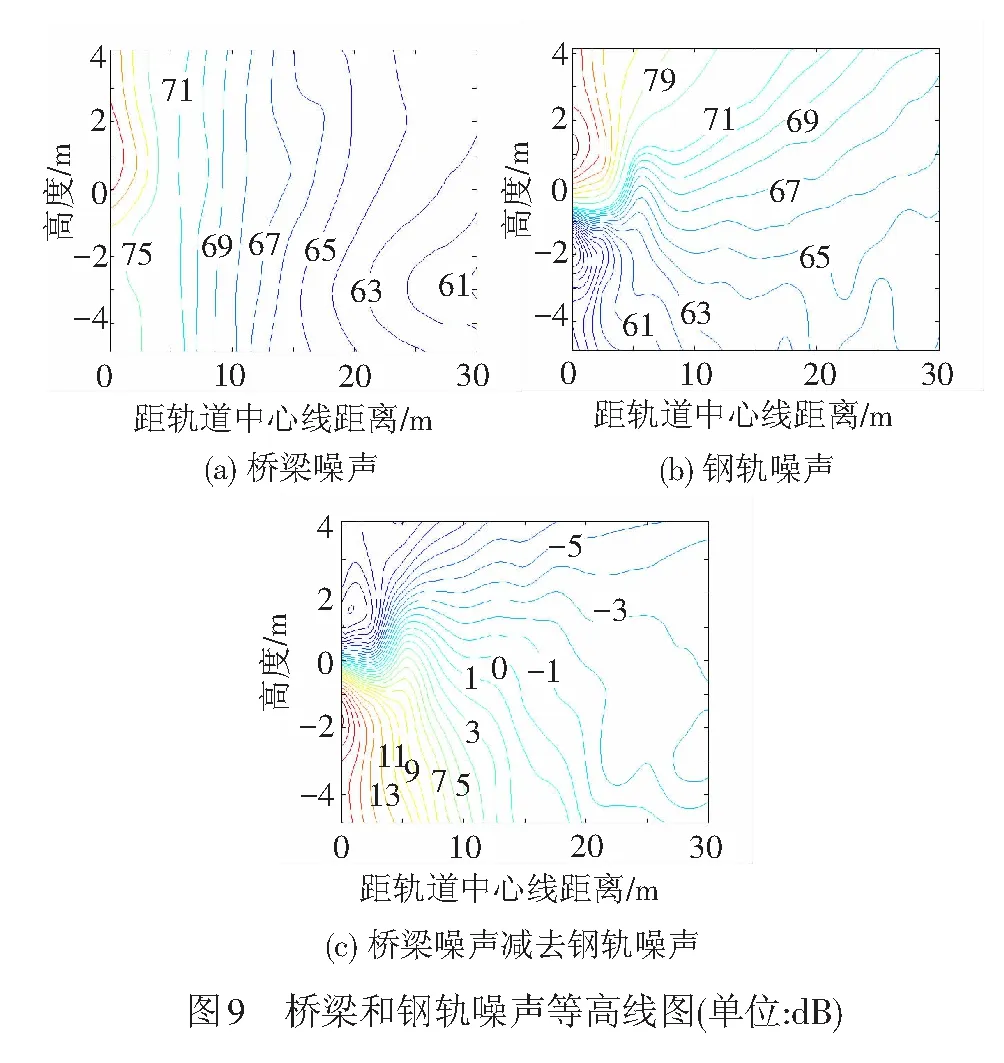
为了更清晰地对比桥梁和钢轨辐射噪声的空间分布，图9 给出了桥梁、钢轨噪声以及两者之差的等高线分布图，原点设在U梁底板中心位置，其中图9(c)中的值由图9(a)减去图9(b)获得。由图9可见，桥梁辐射噪声主要在U梁下方空间占主导地位，而钢轨辐射噪声受到U 梁腹板的遮蔽，主要对其上部空间有较大影响。随着距离桥梁越来越远，钢轨辐射噪声所占比重越来越大，到20 m处两者已经基本持平，在30 m处钢轨噪声比桥梁噪声大3 dB左右。因此，当采用A计权声压级评价轨道交通桥梁总噪声水平时，必须同时考虑钢轨噪声和桥梁噪声的影响。

5 结束语

本文提出了结合3D车-轨-桥耦合振动和2.5D声学模型计算桥梁和钢轨中低频噪声的方法，然后运用这一方法预测了轨道交通U梁和钢轨的噪声，并通过实测验证了数值计算方法的精度，最后对桥梁噪声和钢轨噪声的特性及空间分布进行了研究。本文的研究表明，对文中的模型和参数，桥梁结构噪声主要在U梁下方起主导作用，而钢轨噪声在U梁上方贡献更大。在进行噪声预测时，两者的贡献均不能忽略。

参考文献：

[1] 冯登宇，耿传智. 城市轨道交通高架线噪声实测及传播规律研究[J]. 现代城市轨道交通，2015(5)：40-44.

FENG Dengyu, GENG Chuanzhi. Study on Measurement and Patterns of Propagation of Elevated Line Noise in Urban Rail Transit[J]. Modern Urban Transit, 2015(5):40-44.

[2] LI Q, LI W Q, WU D J, et al. A Combined Power Flow and Infinite Element Approach to the Simulation of Medium-frequency Noise Radiated from Bridges and Rails[J]. Journal of Sound and Vibration, 2016, 365:134-156.

[3] THOMPSON D J. Predictions of Acoustic Radiation From Vibrating Wheels and Rails[J]. Journal of Sound and Vibration, 1988, 120(2):275-280.

[4] 刘林芽，雷晓燕，练松良. 铁路轮轨噪声预测分析[J]. 噪声与振动控制,2008，28(2)：73-78.

LIU Linya, LEI Xiaoyan, LIAN Songliang. Prediction and Analysis of Wheel/Rail Noise for the Railway[J]. Noise and Vibration Control, 2008, 28(2):73-78.

[5] 方锐，肖新标，房建英，等. 轨道结构参数对其声辐射特性影响[J].铁道学报，2011，33(5)：78-84.

FANG Rui, XIAO Xinbiao, FANG Jianying, et al. Influence of Track Structure Parameters on Acoustic Radiation[J]. Journal of the China Railway Society, 2011, 33(5):78-84.

[6] 张迅，李小珍，刘德军，等. 高速铁路32 m简支箱梁声辐射特性研究[J]. 铁道学报，2012，34(7)：96-102.

ZHANG Xun, LI Xiaozhen, LIU Dejun, et al. Sound Radiation Characteristics of 32 m Simply Supported Concrete Box Girder Applied in High-speed Railway[J]. Journal of the China Railway Society, 2012, 34(7):96-102.

[7] LI Q, XU Y L, WU D J. Concrete Bridge-Borne Low-frequency Noise Simulation Based on Vehicle-Track-Bridge Dynamic Interaction[J.] Journal of Sound and Vibration, 2012, 331(10):2457-2470.

[8] 李晶，张楠，张立彬.高架桥梁振动与结构噪声数值模拟[J]. 环境工程，2012，30(S1)：156-160.

LI Jing, ZHANG Nan, ZHANG Libin. Numerical Simulation of the Vibration and Structure-Borne Noise of the Viaduct[J]. Environmental Engineering, 2012,30(S1):156-160.

[9] 石广田，杨新文，张小安，等. 高铁板式轨道区段箱梁结构噪声辐射分析[J].噪声与振动控制，2015，35(1)：160-164.

SHI Guangtian, YANG Xinwen, ZHANG Xiaoan, et al. Noise Radiation Analysis of Box-girder Structure in Slab Track Section of High Speed Railways[J]. Noise and Vibration Control, 2015,35(1):160-164.

[10] WU T X, LIU J H. Sound Emission Comparisons between the Box-section and U-section Concrete Viaducts for Elevated Railway[J]. Noise Control Engineering Journal, 2012, 60(4):450-457.

[11] LI Q, SONG X D, WU D J. A 2.5-dimensional Method for the Prediction of Structure-Borne Low-frequency Noise from Concrete Rail Transit Bridges[J]. Journal of the Acoustical Society of America 2014, 135(5):2718-2726.

[12] 宋晓东，吴定俊，李奇.基于无限元的2.5维方法预测轨道交通混凝土桥梁低频噪声[J].振动工程学报，2015，28(6)：929-936.

SONG Xiaodong, WU Dingjun, LI Qi. A 2.5-dimensional Infinite Element Based Method for the Prediction of Structure-borne Low-frequency Noise from Concrete Rail Transit Bridges[J]. Journal of Vibration Engineering, 2015, 28(6):929-936.

[13] 李小珍，刘全民，宋立忠，等.高速铁路钢桁结合梁桥结构噪声预测研究[J].铁道学报，2014，36(12)：97-103.

LI Xiaozhen, LIU Quanmin, SONG Lizhong, et al. Prediction of Structure-Borne Noise of Composite Steel Truss Bridge of High-speed Railway[J]. Journal of the China Railway Society, 2014, 36(12):97-103.

[14] LI Q, XU Y L, WU D J, et al. Computer-aided Nonlinear Vehicle-bridge Interaction Analysis[J]. Journal of Vibration and Control, 2010, 16(12):1791-1816.

[15] International Organization for Standardization.ISO 3095 2005:Railway Applications-Acoustics-Measurement of Noise Emitted by Rail Bound Vehicles[S]. Britain：British Standards Institution, 2006.

[16] THOMPSON D J. Railway Noise and Vibration:Mechanisms, Modeling and Means of Control[M]. Oxford:Elsevier, 2009:148-150.

[17] DUHAMEL D. Efficient Calculation of the Three-dimensional Sound Pressure Field around a Noise Barrier[J]. Journal of Sound and Vibration, 1996, 197(5):547-571.